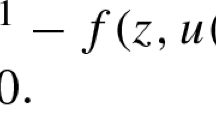Skip to main content
SpringerLink
Log in

Existence of Solutions for the Dirichlet Problem with Superlinear Nonlinearities

  • Published:
Czechoslovak Mathematical Journal Aims and scope Submit manuscript

Abstract

In this paper we establish the existence of nontrivial solutions to

$$\frac{d}{{dt}}L_{x'} \left( {t,x'\left( t \right)} \right) + {\text{V}}_x \left( {t,x\left( t \right)} \right) = 0,x\left( 0 \right) = x\left( T \right)$$

with V x superlinear in x.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Capietto, J. Mawhin and F. Zanolin: Boundary value problems for forced superlinear second order ordinary differential equations. Nonlinear Partial Differential Equations and Their Applications. College de France Seminar, Vol. XII. Pitman Res. Notes ser., 302, 1994, pp. 55–64.

    Google Scholar 

  2. A. Castro, J. Cossio and J. M. Neuberger: A sign-changing solution for a superlinear Dirichlet problem. Rocky Mountain J. Math. 27 (1997), 1041–1053.

    Google Scholar 

  3. S. K. Ingram: Continuous dependence on parameters and boundary value problems. Pacific J. Math. 41 (1972), 395–408.

    Google Scholar 

  4. G. Klaasen: Dependence of solutions on boundary conditions for second order ordinary differential equations. J. Differential Equations 7 (1970), 24–33.

    Google Scholar 

  5. L. Lassoued: Periodic solutions of a second order superquadratic systems with a change of sign in the potential. J. Differential Equations 93 (1991), 1–18.

    Google Scholar 

  6. J. Mawhin: Problèmes de Dirichlet Variationnels Non Linéares. Les Presses de l'Université de Montréal, 1987.

  7. A. Nowakowski: A new variational principle and duality for periodic solutions of Hamilton's equations. J. Differential Equations 97 (1992), 174–188.

    Google Scholar 

  8. P. H. Rabinowitz: Minimax Methods in Critical Points Theory with Applications to Differential Equations. AMS, Providence, 1986.

  9. D. O'Regan: Singular Dirichlet boundary value problems. I. Superlinear and nonresonant case. Nonlinear Anal. 29 (1997), 221–245.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics, University of Łódź, Banacha 22, 90-238, Łódź, Poland

    Andrzej Nowakowski & Andrzej Rogowski

Authors
  1. Andrzej Nowakowski
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrzej Rogowski
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nowakowski, A., Rogowski, A. Existence of Solutions for the Dirichlet Problem with Superlinear Nonlinearities. Czechoslovak Mathematical Journal 53, 515–528 (2003). https://doi.org/10.1023/B:CMAJ.0000024499.27359.ce

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:CMAJ.0000024499.27359.ce

Search

Navigation