Abstract
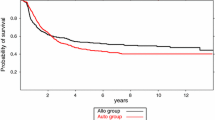
A common approach to testing for differences between the survival rates of two therapies is to use a proportional hazards regression model which allows for an adjustment of the two survival functions for any imbalance in prognostic factors in the comparison. When the relative risk of one treatment to the other is not constant over time the question of which therapy has a survival advantage is difficult to determine from the Cox model. An alternative approach to this problem is to plot the difference between the two predicted survival functions with a confidence band that provides information about when these two treatments differ. Such a band will depend on the covariate values of a given patient. In this paper we show how to construct a confidence band for the difference of two survival functions based on the proportional hazards model. A simulation approach is used to generate the bands. This approach is used to compare the survival probabilities of chemotherapy and allogeneic bone marrow transplants for chronic leukemia.
Similar content being viewed by others
References
O. O. Aalen, “A linear regression model for the analysis of life times,” Statistics in Medicine vol. 8 pp. 907-925, 1989.
P. K. Andersen, “Testing goodness of fit of Cox's regression and life mode,” Biometrics vol. 38 pp. 67-77, 1982. Correction: vol. 40 pp. 1217, 1984.
P. K. Andersen, O. Borgan, R. D. Gill, and N. Keiding, Statistical Models Based on Counting Processes, Spring-Verlag, New York, 1993.
P. K. Andersen and R. D. Gill, “Cox's regression model for counting processes: a large sample study,” The Annual of Statistics vol. 10 pp. 1100-1120, 1982.
E. A. Arjas, “Graphical method for assessing goodness of fit in Cox's proportional hazards model,” Journal of the American Statistical Association vol. 83 pp. 204-212, 1988.
N. Breslow, “Analysis of survival data under the proportional hazards model,” International Statistical Review vol. 43 pp. 45-58, 1975.
D. R. Cox, “Regression models and life tables (with discussion),” Journal of the Royal Statistical Society, Series B vol. 34 pp. 187-220, 1972.
D. M. Dabrowska, K. A. Doksum, and J-K. Song, “Graphical comparison of cumulative hazards for two populations,” Biometrika vol. 76 pp. 763-773, 1989.
D. M. Dabrowska, K. A. Doksum, N. J. Feduska, R. Husing and P. Neville, “Methods for comparing cumulative hazard functions in a semi-proportional hazard model,” Statistics in Medicine vol. 11 pp. 1465-1476, 1992.
R. B. Gale, R. Helmann, M. J. Zhang, J. Hasford, J. M. Goldman, H. Heimpel, J. P. Klein, H. J. Kolb, P. B. McGlave, J. R. Passweg, P. A. Rowlings, K. A. Sobocinski, M. M. Horowitz, and the German CML Study Group, “Survival with bone marrow transplantation versus hydroxyurea or interferon for chronic myelogenous leukemia (CML),” Blood vol. 91 pp. 1810-1819, 1998.
E. L. Kaplan and P. Meier, “Nonparametric estimation from incomplete observations,” Journal of the American Statistical Association vol. 53 pp. 457-481, 1958.
J. P. Klein and M. J. Zhang, “Statistical challenges in comparing chemotherapy and bone marrow transplantation as a treatment for leukemia,” in Lifetime Data: Models in Reliability and Survival Analysis, (N. P. Jewell et al., eds.), Kluwer Academic Publishers: Boston, 1996, pp. 175-185.
T. L. Lai and Z. Ying, “Estimating a distribution function with truncated and censored data,” The Annual of Statistics vol. 19 pp. 417-442, 1991.
D. Y. Lin, “Goodness of fit for the Cox regression model based on a class of parameter estimators,” Journal of the American Statistical Association vol. 86 pp. 725-728, 1991.
D. Y. Lin, T. R. Fleming and L. J. Wei, “Confidence bands for survival curves under the proportional hazards model,” Biometrika vol. 81 pp. 73-81, 1994.
M. I. Parzen, L. J. Wei and Z. Ying, “Simultaneous confidence intervals for the difference of two survival functions,” Scandinavian Journal of Statistics vol. 24 pp. 309-314, 1997.
L. J. Wei, “Testing goodness-of-fit for the proportional hazards model with censored observations,” Journal of the American Statistical Association vol. 79 pp. 649-652, 1984.
M. Woodroofe, “Estimating a distribution function with truncated data,” The Annual of Statistics vol. 13 pp. 163-177, 1985.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Zhang, MJ., Klein, J.P. Confidence Bands for the Difference of Two Survival Curves Under Proportional Hazards Model. Lifetime Data Anal 7, 243–254 (2001). https://doi.org/10.1023/A:1011636407958
Issue Date:
DOI: https://doi.org/10.1023/A:1011636407958