Skip to main content
SpringerLink
Log in

A Geometric Unification of Constrained System Dynamics

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

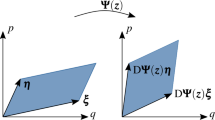
A unified geometric formulation of the methods used for solving constrained system problems is given. Both holonomic and nonholonomic systems are treated in like manner, and the dynamic equations are expressible in either generalized velocities or quasi-velocities. Moreover, a wide range of ’unconstrained‘ systems are uniformly regarded as generalized particles in the multi-dimensional metric spaces relating to their configuration. The derivation is grounded on the tensor calculus formalism and appropriate geometric interpretations are reported. In its useful matrix form, the formulation turns out short, elementary and general. This unified geometric approach to constrained system dynamics may deserve to become a generally accepted method inacademic and engineering applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Orlandea, N., Chace, M.A. and Calahan, D.A., ‘A sparsity-oriented approach to the dynamic analysis and design of mechanical systems, Parts I and II’, Journal of Engineering for Industry 99, 1977, 773–784.

    Google Scholar 

  2. Wittenburg, J., Dynamics of Systems of Rigid Bodies, Teubner, Stuttgart, 1977.

    Google Scholar 

  3. Wehage, R.A. and Haug, E.J., ‘Generalized co-ordinate partitioning for dimension reduction in analysis of constrained dynamic systems’, Journal of Mechanical Design 104, 1982, 247–255.

    Google Scholar 

  4. Nikravesh, P.E., Computer-Aided Analysis of Mechanical Systems, Prentice Hall, Englewood Cliffs, 1988.

    Google Scholar 

  5. Kim, S.S. and Vanderploeg, M.J., ‘A general and efficient method for dynamic analysis of mechanical systems using velocity transformations’, Journal of Mechanisms Transmissions, and Automation in Design 108, 1986, 177–182.

    Google Scholar 

  6. Hemami, H. and Weimer, F.C., ‘Modelling of nonholonomic dynamic systems with applications’, Journal of Applied Mechanics 48, 1981, 177–182.

    Google Scholar 

  7. Wampler, C., Buffinton, K. and Shu-hui, J., ‘Formulation of equations of motion for systems subject to constraints’, Journal of Applied Mechanics 52, 1985, 465–470.

    Google Scholar 

  8. García de Jalón, J., Unda, J. and Avello, A., ‘Natural co-ordinates for the computer analysis of multibody systems’, Computer Methods in Applied Mechanics and Engineering 56, 1986, 309–327.

    Google Scholar 

  9. García de Jalón, J., Unda, J., Avello, A. and Jiménez, J.M., ‘Dynamic analysis of threedimensional mechanisms in “natural” co-ordinates’, Journal of Mechanisms, Transmissions, and Automation in Design 109, 1987, 460–465.

    Google Scholar 

  10. Walton, Jr., W.C. and Steeves, E.C., ‘A new matrix theorem and its application for establishing independent co-ordinates for complex dynamical systems with constraints’, NASA Technical Report TR R-326, 1969.

  11. Mani, N.K., Haug, E.J. and Atkinson, K.E., ‘Application of singular value decomposition for analysis of mechanical system dynamics’, Journal of Mechanisms, Transmissions, and Automation in Design 107, 1985, 82–87.

    Google Scholar 

  12. Singh, C.L. and Likins, P.W., ‘Singular value decomposition for constrained dynamical systems, Journal of Applied Mechanics 52, 1985, 943–948.

    Google Scholar 

  13. Kim, S.S. and Vanderploeg, M.J., ‘QR decomposition for state space representation of constrained mechanical dynamic systems’, Journal of Mechanisms, Transmissions, and Automation inDesign 108, 1986, 183–188.

    Google Scholar 

  14. Amirouche, F.M.L., Jia, T. and Ider, S.K., ‘A recursive Householder transformation for complex dynamical systems with constraints’, Journal of Applied Mechanics 55, 1988, 729–734.

    Google Scholar 

  15. Liang, C.G. and Lance, G.M., ‘A differentiable null space method for constrained dynamic analysis’, Journal of Mechanisms, Transmissions, and Automation in Design 109, 1987, 405–411.

    Google Scholar 

  16. Agrawal, O.P. and Saigal, S., ‘Dynamic analysis of multi-body systems using tangent coordinates’, Computers & Structures 31, 1989, 349–355.

    Google Scholar 

  17. Kane, T.R. and Levinson, D.A., ‘Formulation of equations of motion for complex spacecraft’, Journal of Guidance and Control 3, 1980, 99–112.

    Google Scholar 

  18. Desloge, D.A., ‘The Gibbs–Appell equations of motion’, American Journal of Physics 56, 1988, 841–846.

    Google Scholar 

  19. Kurdila, A., Papastavridis, J.G. and Kamat, M.P., ‘Role of Maggi's equations in computational methods for constrained multibody systems’, Journal of Guidance, Control, and Dynamics 13, 1990, 113–120.

    Google Scholar 

  20. Schiehlen, W. (ed.), Multibody System Handbook, Springer-Verlag, Berlin, 1990.

    Google Scholar 

  21. Scott, D., ‘Can a projection method of obtaining equations of motion compete with Lagrange's equations?’, American Journal of Physics 56, 1988, 451–456.

    Google Scholar 

  22. Lesser, M., ‘A geometrical interpretation of Kane's equations’, Proceedings of the Royal Society, London A436, 1992, 69–87.

    Google Scholar 

  23. Essén, H., ‘On the geometry of nonholonomic dynamics’, Journal of Applied Mechanics 61, 1994, 689–694.

    Google Scholar 

  24. Synge, J.L. and Schild, A., Tensor Calculus, University of Toronto Press, Toronto, 1949.

    Google Scholar 

  25. Arnold, V.I., Mathematical Methods of Classical Mechanics, Springer-Verlag, New York, 1989.

    Google Scholar 

  26. Maisser, P., ‘Analytische Dynamik von Mehrkörpersystemen’, ZAMM (Zeitschrift f ¨ur Angewandte Mathematik und Mechanik) 68, 1988, 463–481.

    Google Scholar 

  27. Cardin, F. and Zanzotto, G., ‘On constrained mechanical systems: D'Alembert's and Gauss' principles’, Journal of Mathematical Physics 30, 1989, 1473–1479.

    Google Scholar 

  28. Pobedrya, B.E., Lectures on Tensor Analysis, Moscow University Publishers, Moscow, 1974.

    Google Scholar 

  29. Petzold, L.R., ‘Methods and software for differential-algebraic systems’, in Real-Time Integration Methods for Mechanical System Simulations, E.J. Haug and R.C. Deyo (eds.), NATO ASI Series F, Vol. 69, Springer-Verlag, Berlin, 1990, 127–140.

    Google Scholar 

  30. Baumgarte, J., ‘Stabilization of constraints and integrals of motion in dynamical systems, Computer Methods in Applied Mechanics and Engineering 1, 1972, 1–16.

    Google Scholar 

  31. Blajer, W., ‘A projection method approach to constrained dynamic analysis’, Journal of Applied Mechanics 59, 1992, 643–649.

    Google Scholar 

  32. Neimark, J.I. and Fufaev, N.A., Dynamics of Nonholonomic Systems [in Russian], Moscow University Publishers, Moscow, 1967.

    Google Scholar 

  33. Blajer, W., ‘Projective formulation of Maggi's method for nonholonomic systems analysis’, Journal of Guidance, Control, and Dynamics 15, 1992, 522–525.

    Google Scholar 

  34. Blajer, W., Schiehlen, W. and Schirm, W., ‘Projective criterion to the co-ordinate partitioning method for multibody dynamics’, Archive of Applied Mechanics 64, 1994, 86–98.

    Google Scholar 

  35. Blajer, W., ‘An orthonormal tangent space method for constrained multibody systems’, Computer Methods in Applied Mechanics and Engineering 121, 1995, 45–57.

    Google Scholar 

  36. Arczewski, K. and Blajer, W., ‘A unified approach to the modelling of holonomic and nonholonomic mechanical systems’, Mathematical Modelling of Systems 2, 1996, 157–174.

    Google Scholar 

  37. De Boer, R., Vector-und Tensorrechnung für Ingenieure, Springer-Verlag, Berlin, 1982.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, Technical University of Radom, ul. Malczewskiego 29, PL-26-600, Radom, Poland

    Wojciech Blajer

Authors
  1. Wojciech Blajer
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Blajer, W. A Geometric Unification of Constrained System Dynamics. Multibody System Dynamics 1, 3–21 (1997). https://doi.org/10.1023/A:1009759106323

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1009759106323

Search

Navigation