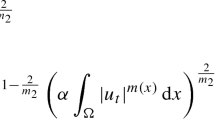Abstract
In this paper we consider the existence and asymptotic behavior of solutions of the following problem:
where q>1, q⩾1, δ>0, α>0, β⩾0, \(\mu \in {\mathbb{R}}\) is the Laplacian in \({\mathbb{R}}^N\).
Similar content being viewed by others
References
E. H. Brito: Nonlinear Initial Boundary Value Problems. Nonlinear Anal. 11 (1987), 125–137.
C. Corduneanu: Principles of Differential and Integral Equations. Chelsea Publishing Company, The Bronx, New York, 1977.
R. Ikehata: On the Existence of Global Solutions for some Nonlinear Hyperbolic Equations with Neumann Conditions. T R U Math. 24 (1988), 1–17.
T. Matsuyama, R. Ikehata: On Global Solutions and Energy Decay for the Wave Equations of Kirchhoff type with Nonlinear Damping terms. J. Math. Anal. Appl. 204 (1996), 729–753.
M. Nakao: Asymptotic Stability of the Bounded or Almost Periodic Solutions of the Wave Equations with Nonlinear Damping terms. J. Math. Anal. Appl. 58 (1977), 336–343.
K. Narasimha: Nonlinear Vibration of an Elastic String. J. Sound Vibration 8 (1968), 134–146.
K. Nishihara, Y. Yamada: On Global Solutions of some Degenerate Quasilinear Hyperbolic Equation with Dissipative Damping terms. Funkcial. Ekvac. 33 (1990), 151–159.
K. Ono: Global Existence, Decay and Blowup of Solutions for some Mildly Degenerate Nonlinear Kirchhoff Strings. J. Differential Equations 137 (1997), 273–301.
M. D. Silva Alves: Variational Inequality for a Nonlinear Model of the Oscillations of Beams. Nonlinear Anal. 28 (1997), 1101–1108.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Park, J.Y., Bae, J.J. On solutions of quasilinear wave equations with nonlinear damping terms. Czechoslovak Mathematical Journal 50, 565–585 (2000). https://doi.org/10.1023/A:1022889711817
Issue Date:
DOI: https://doi.org/10.1023/A:1022889711817