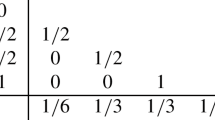
Abstract
In the past few years, a number of Lie-group methods based on Runge—Kutta schemes have been proposed. One might extrapolate that using a selfadjoint Runge—Kutta scheme yields a Lie-group selfadjoint scheme, but this is generally not the case: Lie-group methods depend on the choice of a coordinate chart which might fail to comply to selfadjointness.
In this paper we discuss Lie-group methods and their dependence on centering coordinate charts. The definition of the adjoint of a numerical method is thus subordinate to the method itself and the choice of the chart. We study Lie-group numerical methods and their adjoints, and define selfadjoint numerical methods. The latter are defined in terms of classical selfadjoint Runge—Kutta schemes and symmetric coordinates, based on geodesic or on flow midpoint. As result, the proposed selfadjoint Lie-group numerical schemes obey time-symmetry both for linear and nonlinear problems.
Similar content being viewed by others
REFERENCES
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover, New York, 1965.
M. P. Calvo, A. Iserles, and A. Zanna, Numerical solution of isospectral flows, Math. Comp., 66 (1997), pp. 1461-1486.
F. Diele, L. Lopez, and R. Peluso, The Cayley transform in the numerical solution of unitary differential systems, Adv. Comput. Math., 8:4 (1998), pp. 317-334.
K. Engø, On the construction of geometric integrators in the RKMK class, BIT, 40:1 (2000), pp. 41-61.
K. Engø and S. Faltinsen, Numerical integration of Lie-Poisson systems while preserving coadjoint orbits and energy, Reports in Informatics No. 179, Department of Informatics, University of Bergen, Norway, October 1999.
H. Flaschka, The Toda lattice I, Phys. Rev., B9 (1974), pp. 1924-1925.
E. Hairer, Backward analysis of numerical integrators and symplectic methods, Ann. Numer. Math., 1 (1994), pp. 107-132.
E. Hairer, S. P. Nørsett, and G. Wanner, Solving Ordinary Differential Equations I. Nonstiff Problems, 2nd ed., Springer-Verlag, Berlin, 1993.
F. Hausdorff, Die symbolische Exponentialformel in der Gruppentheorie, Berichte der Sächsischen Akademie der Wissenschaften (Math. Phys. Klasse), 58 (1906), pp. 19-48
S. Helgason, Differential Geometry, Lie Groups and Symmetric Spaces, Academ ic Press, New York, 1978.
A. Iserles, H. Munthe-Kaas, S. P. Nørsett, and A. Zanna, Lie-group methods, Acta Numerica, 9 (2000), pp. 215-365.
A. Iserles and S. P. Nørsett, On the solution of differential equations in Lie groups, Phil. Trans. R. Soc. Lond. A, 357 (1999), pp. 983-1019.
A. Iserles, S. P. Nørsett, and A. Rasmussen, On the reversibility of the canonical Magnus expansion, Technical Report NA 1998/ 06, DAMTP, University of Cambridge, UK, 1998.
J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry, Springer-Verlag, Berlin, 1994.
R. I. McLachlan, Explicit Lie-Poisson integration and the Euler equations, Phys. Rev. Lett., 71 (1993), pp. 3043-3046.
R. I. McLachlan, On the numerical integration of ordinary differential equations by symmetric composition methods, SIAM J. Sci. Comput., 16 (1995), pp. 151-168.
J. Moser, Stable and Random Motion in Dynamical Systems, Princeton University Press, Princeton, NJ, 1973.
H. Munthe-Kaas, High order Runge-Kutta methods on manifolds, J. Appl. Numer. Math., 29 (1999), pp. 115-127.
H. Munthe-Kaas and B. Owren, Computations in a free Lie algebra, Phil. Trans. R. Soc. Lond. A, 357 (1999), pp. 957-982.
H. Munthe-Kaas and A. Zanna, Numerical integration of differential equations on homogeneous manifolds, in F. Cucker, ed., Foundations of Computational Mathematics, Springer-Verlag, Berlin, 1997, pp. 305-315.
B. Owren and A. Marthinsen, Integration methods based on canonical coordinates of the second kind, Technical Report Numerics No. 5/ 1999, Department of Mathematical Sciences, The Norwegian University of Science and Technology, Trondheim, Norway, 1999.
A. M. Stuart and A. R. Humphries, Dynamical Systems and Numerical Analysis, Cambridge University Press, Cambridge, 1996.
M. Toda, Theory of Nonlinear Lattices, Springer-Verlag, Berlin, 1981.
H. Yoshida. Construction of higher order symplectic integrators, Phys. Lett. A, 150 (1990), pp. 262-268.
A. Zanna, On the Numerical Solution of Isospectral Flows, PhD thesis, Newnham College, University of Cambridge, UK, 1998.
A. Zanna, Collocation and relaxed collocation for the Fer and the Magnus expansions, SIAM J. Numer. Anal., 36:4 (1999), pp. 1145-1182.
A. Zanna, K. Engø, and H. Z. Munthe-Kaas, Adjoint and selfadjoint Lie-group methods, Technical Report NA 1999/ 02, DAMTP, University of Cambridge, UK, 1999.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Zanna, A., Engø, K. & Munthe-Kaas, H.Z. Adjoint and Selfadjoint Lie-group Methods. BIT Numerical Mathematics 41, 395–421 (2001). https://doi.org/10.1023/A:1021950708869
Issue Date:
DOI: https://doi.org/10.1023/A:1021950708869