Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-28T06:42:46.707Z Has data issue: false hasContentIssue false
  • English
  • Français

A concrete model for a typed linear algebraic lambda calculus

Published online by Cambridge University Press:  21 November 2023

Alejandro Díaz-Caro Open the ORCID record for Alejandro Díaz-Caro [Opens in a new window]  and
Octavio Malherbe
Alejandro Díaz-Caro*
Affiliation:
CONICET-Universidad de Buenos Aires, Instituto de Ciencias de la Computación (ICC), Buenos Aires, Argentina Departamento de Ciencia y Tecnología, Universidad Nacional de Quilmes, Bernal, Buenos Aires, Argentina
Octavio Malherbe
Affiliation:
IMERL, Facultad de Ingeniería, Universidad de la República, Montevideo, Uruguay
*
Corresponding author: Alejandro Díaz-Caro; Email: adiazcaro@conicet.gov.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an adequate, concrete, categorical-based model for Lambda-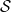${\mathcal S}$, which is a typed version of a linear-algebraic lambda calculus, extended with measurements. Lambda-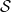${\mathcal S}$ is an extension to first-order lambda calculus unifying two approaches of non-cloning in quantum lambda-calculi: to forbid duplication of variables and to consider all lambda-terms as algebraic linear functions. The type system of Lambda-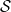${\mathcal S}$ has a superposition constructor S such that a type A is considered as the base of a vector space, while SA is its span. Our model considers S as the composition of two functors in an adjunction relation between the category of sets and the category of vector spaces over 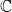$\mathbb C$. The right adjoint is a forgetful functor U, which is hidden in the language, and plays a central role in the computational reasoning.

Keywords

Quantum computingalgebraic lambda-calculuscategorical semantics
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 34 , Issue 1 , January 2024 , pp. 1 - 44
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Partially founded by PICT projects 2019-1272 and 2021-I-A-00090, PIP project 1220200100368CO, and CSIC-UdelaR project 22520220100073UD.

This paper is the long journal version of (Díaz-Caro and Malherbe, 2019). In the present paper, the main new result is to revisit some rewrite rules in order to prove a theorem of adequacy.

References

Abramsky, S. (1993). Computational interpretations of linear logic. Theoretical Computer Science 111 (1) 3–57.CrossRefGoogle Scholar
Abramsky, S. and Coecke, B. (2004). A categorical semantics of quantum protocols. In Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science (LICS). IEEE, 415–425.CrossRefGoogle Scholar
Altenkirch, T. and Grattage, J. (2005). A functional quantum programming language. In Proceedings of the 20th Annual IEEE Symposium on Logic in Computer Science (LICS). IEEE, 249–258.CrossRefGoogle Scholar
Arrighi, P. and Díaz-Caro, A. (2012). A System F accounting for scalars. Logical Methods in Computer Science 8 (1) 11.Google Scholar
Arrighi, P., Díaz-Caro, A. and Valiron, B. (2017). The vectorial lambda-calculus. Information and Computation 254 (1) 105–139.CrossRefGoogle Scholar
Arrighi, P. and Dowek, G. (2017). Lineal: A linear-algebraic lambda-calculus. Logical Methods in Computer Science 13 (1) 8.Google Scholar
Assaf, A., Díaz-Caro, A., Perdrix, S., Tasson, C. and Valiron, B. (2014). Call-by-value, call-by-name and the vectorial behaviour of the algebraic λ-calculus. Logical Methods in Computer Science 10 (4) 8.Google Scholar
Benton, N. (1994). A mixed linear and non-linear logic: Proofs, terms and models. In Pacholski, L. and Tiuryn, J. (eds.) Computer Science Logic (CSL 1994). Lecture Notes in Computer Science, vol. 933. Berlin, Heidelberg: Springer, 121–135.Google Scholar
Díaz-Caro, A. and Dowek, G. (2017). Typing quantum superpositions and measurement. In Theory and Practice of Natural Computing (TPNC 2017). Lecture Notes in Computer Science, vol. 10687. Cham: Springer, 281–293.CrossRefGoogle Scholar
Díaz-Caro, A., Dowek, G., and Rinaldi, J. (2019a). Two linearities for quantum computing in the lambda calculus. BioSystems, 186 104012. Postproceedings of TPNC 2017.CrossRefGoogle ScholarPubMed
Díaz-Caro, A., Guillermo, M., Miquel, A. and Valiron, B. (2019b). Realizability in the unitary sphere. In Proceedings of the 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2019), 1–13.CrossRefGoogle Scholar
Díaz-Caro, A. and Malherbe, O. (2019). A concrete categorical semantics for Lambda-S. In Accattoli, B. and Olarte, C. (eds.) Proceedings of the 13th Workshop on Logical and Semantic Frameworks with Applications (LSFA’18). Electronic Notes in Theoretical Computer Science, vol. 344. Elsevier, 83–100.CrossRefGoogle Scholar
Díaz-Caro, A. and Malherbe, O. (2020). A categorical construction for the computational definition of vector spaces. Applied Categorical Structures 28 (5) 807–844.CrossRefGoogle Scholar
Díaz-Caro, A. and Martínez, G. (2018). Confluence in probabilistic rewriting. In Alves, S. and Wassermann, R. (eds.) Proceedings of the 12th International Workshop on Logical and Semantic Frameworks with Applications (LSFA 2017). Electronic Notes in Teoretical Computer Science, vol. 338, 115–131. Elsevier.CrossRefGoogle Scholar
Díaz-Caro, A. and Petit, B. (2012). Linearity in the non-deterministic call-by-value setting. In Ong, L. and de Queiroz, R. (eds.) Logic, Language, Information and Computation. Lecture Notes in Computer Science, vol. 7456. Berlin, Heidelberg: Springer, 216–231.Google Scholar
Girard, J.-Y. (1987). Linear logic. Theoretical Compututer Science 50 1–102.CrossRefGoogle Scholar
Giry, M. (1982). A categorical approach to probability theory. In Categorical Aspects of Topology and Analysis. Lecture Notes in Mathematics, vol. 915. Springer, 68–85.CrossRefGoogle Scholar
Green, A. S., Lumsdaine, P. L., Ross, N. J., Selinger, P. and Valiron, B. (2013). Quipper: A scalable quantum programming language. ACM SIGPLAN Notices (PLDI’13) 48 (6) 333–342.CrossRefGoogle Scholar
Mac Lane, S. (1998). Categories for the Working Mathematician, 2nd edn. Springer.Google Scholar
Moggi, E. (1988). Computational lambda-calculus and monads. Technical Report ECS-LFCS-88-66, Lab. for Foundations of Computer Science, University of Edinburgh.Google Scholar
Pagani, M., Selinger, P. and Valiron, B. (2014). Applying quantitative semantics to higher-order quantum computing. ACM SIGPLAN Notices (POPL’14) 49 (1) 647–658.CrossRefGoogle Scholar
Selinger, P. (2007). Dagger compact closed categories and completely positive maps. In 3rd International Workshop on Quantum Programming Languages (QPL 2005). Electronic Notes in Theoretical Computer Science, vol. 170, 139–163.CrossRefGoogle Scholar
Selinger, P. and Valiron, B. (2006). A lambda calculus for quantum computation with classical control. Mathematical Structures in Computer Science 16 (3) 527–552.CrossRefGoogle Scholar
Vaux, L. (2009). The algebraic lambda calculus. Mathematical Structures in Computer Science 19 1029–1059.CrossRefGoogle Scholar
Zorzi, M. (2016). On quantum lambda calculi: a foundational perspective. Mathematical Structures in Computer Science 26 (7) 1107–1195.CrossRefGoogle Scholar