Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-01T04:13:17.392Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SET OF ELEMENTARY TENSORS IS WEAKLY CLOSED IN PROJECTIVE TENSOR PRODUCTS

Part of: Topological linear spaces and related structures Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  13 May 2024

COLIN PETITJEAN Open the ORCID record for COLIN PETITJEAN [Opens in a new window]
COLIN PETITJEAN*
Affiliation:
Université Gustave Eiffel, Université Paris Est Creteil, CNRS, LAMA UMR8050, Marne-la-Vallée F-77447, France
*
e-mail: colin.petitjean@univ-eiffel.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the set of elementary tensors is weakly closed in the projective tensor product of two Banach spaces. As a result, we answer a question of Rodríguez and Rueda Zoca [‘Weak precompactness in projective tensor products’, Indag. Math. (N.S.) 35(1) (2024), 60–75], proving that if 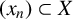$(x_n) \subset X$ and $(y_n) \subset Y$ are two weakly null sequences such that 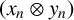$(x_n \otimes y_n)$ converges weakly in 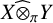$X \widehat {\otimes }_\pi Y$, then $(x_n \otimes y_n)$ is also weakly null.

Keywords

projective tensor productselementary tensorweak convergence

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties
Secondary: 46A32: Spaces of linear operators; topological tensor products; approximation properties 46B10: Duality and reflexivity
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by the French ANR project No. ANR-20-CE40-0006.

References

Diestel, J. and Uhl, J. J., Vector Measures (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
García-Lirola, L., Grelier, G., Martínez-Cervantes, G. and Rueda Zoca, A., ‘Extremal structure of projective tensor products’, Results Math. 78 (2023), Article no. 196, 16 pages.CrossRefGoogle Scholar
García-Lirola, L., Petitjean, C., Procházka, A. and Rueda Zoca, A., ‘Extremal structure and duality of Lipschitz free spaces’, Mediterr. J. Math. 15(2) (2018), Article no. 69, 23 pages.CrossRefGoogle Scholar
García-Lirola, L., Petitjean, C and Rueda Zoca, A., ‘On the structure of spaces of vector-valued Lipschitz functions’, Studia Math. 239(3) (2017), 249–271.CrossRefGoogle Scholar
Rodríguez, J. and Rueda Zoca, A., ‘Weak precompactness in projective tensor products’, Indag. Math. (N.S.) 35(1) (2024), 60–75.CrossRefGoogle Scholar
Ryan, R. A., Introduction to Tensor Products of Banach Spaces, Springer Monographs in Mathematics (Springer-Verlag, London, 2002).CrossRefGoogle Scholar