Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-18T23:55:55.825Z Has data issue: false hasContentIssue false
  • English
  • Français

Internal shear layers from librating objects

Published online by Cambridge University Press:  10 August 2017

Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]  and
Michael Le Bars
Stéphane Le Dizès*
Affiliation:
CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, F-13013 Marseille, France
Michael Le Bars
Affiliation:
CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, F-13013 Marseille, France
*
†Email address for correspondence: ledizes@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we analyse the internal shear layer structures generated by the libration of an axisymmetric object in an unbounded fluid rotating at a rotation rate 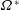$\unicode[STIX]{x1D6FA}^{\ast }$ using direct numerical simulation and small Ekman number asymptotic analysis. We consider weak libration amplitude and libration frequency 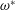$\unicode[STIX]{x1D714}^{\ast }$ within the inertial wave interval 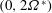$(0,2\unicode[STIX]{x1D6FA}^{\ast })$ such that the fluid dynamics is mainly described by a linear axisymmetric harmonic solution. The internal shear layer structures appear along the characteristic cones of angle 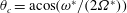$\unicode[STIX]{x1D703}_{c}=\text{acos}(\unicode[STIX]{x1D714}^{\ast }/(2\unicode[STIX]{x1D6FA}^{\ast }))$ which are tangent to the librating object at so-called critical latitudes. These layers correspond to thin viscous regions where the singularities of the inviscid solution are smoothed. We assume that the velocity field in these layers is described by the class of similarity solutions introduced by Moore & Saffman (Phil. Trans. R. Soc. Lond. A, vol. 264, 1969, pp. 597–634). These solutions are characterized by two parameters only: a real parameter 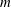$m$, which measures the strength of the underlying singularity, and a complex amplitude coefficient 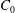$C_{0}$. We first analyse the case of a disk for which a general asymptotic solution for small Ekman numbers is known when the disk is in a solid plane. We demonstrate that the numerical solutions obtained for a free disk and for a disk in a solid plane are both well described by the asymptotic solution and by its similarity form within the internal shear layers. For the disk, we obtain a parameter 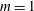$m=1$ corresponding to a Dirac source at the edge of the disk and a coefficient 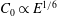$C_{0}\propto E^{1/6}$ where 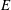$E$ is the Ekman number. The case of a smoothed librating object such as a spheroid is found to be different. By asymptotically matching the boundary layer solution to similarity solutions close to a critical latitude on the surface, we show that the adequate parameter 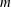$m$ for the similarity solution is 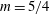$m=5/4$, leading to a coefficient 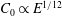$C_{0}\propto E^{1/12}$, that is larger than for the case of a disk for small Ekman numbers. A simple general expression for 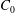$C_{0}$ valid for any axisymmetric object is obtained as a function of the local curvature radius at the critical latitude in agreement with this change of scaling. This result is tested and validated against direct numerical simulations.

JFM classification

Boundary Layers: Boundary layer separation Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 653 - 675
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37, 307–323.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.CrossRefGoogle Scholar
Cébron, D., Le Bars, M., Moutou, C. & Le Gal, P. 2012 Elliptical instability in terrestrial planets and moons. Astron. Astrophys. 539, A78.CrossRefGoogle Scholar
Flynn, M. R., Onu, K. & Sutherland, B. R. 2003 Internal wave excitation by a vertically oscillating sphere. J. Fluid Mech. 494, 65–93.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Gubbins, D. & Roberts, P. H. 1987 Magnetohydrodynamics of the Earth’s core. Geomagnetism 2, 1–183.Google Scholar
Hurley, D. G. & Keady, G. 1997 The generation of internal waves by vibrating elliptic cylinders. Part 2: approximate viscous solution. J. Fluid Mech. 351, 119–138.CrossRefGoogle Scholar
Kerswell, R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.CrossRefGoogle Scholar
Kida, S. 2011 Steady flow in a rapidly rotating sphere with weak precession. J. Fluid Mech. 680, 150–193.CrossRefGoogle Scholar
Klein, M., Seelig, T., Kurgansky, M., Ghasemi, V. A., Borcia, I. D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustrum and a cylinder. J. Fluid Mech. 751, 255–297.CrossRefGoogle Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 035504.CrossRefGoogle Scholar
Le Bars, M., Cébron, D. & Le Gal, P. 2015 Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 47, 163–193.CrossRefGoogle Scholar
Le Dizès, S. 2015 Wave field and zonal flow of a librating disk. J. Fluid Mech. 782, 178–208.CrossRefGoogle Scholar
Machicoane, N., Cortet, P.-P., Voisin, B. & Moisy, F. 2015 Influence of the multipole order of the source on the decay of an inertial wave beam in a rotating fluid. Phys. Fluids 27, 066602.CrossRefGoogle Scholar
Marcotte, F., Dormy, E. & Soward, A. 2016 On the equatorial Ekman layer. J. Fluid Mech. 803, 395–435.CrossRefGoogle Scholar
Margot, J.-L., Peale, S. J., Jurgens, R. F., Slade, M. A. & Holin, I. V. 2007 Large longitude libration of mercury reveals a molten core. Science 316 (5825), 710–714.CrossRefGoogle ScholarPubMed
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–640.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. Lond. A 264, 597–634.Google Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. J. Fluid Mech. 28, 1–16.CrossRefGoogle Scholar
Noir, J., Hemmerlin, F., Wicht, J., Baca, S. M. & Aurnou, J. M. 2009 An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans. Phys. Earth Planet. Inter. 173 (1), 141–152.CrossRefGoogle Scholar
Ogilvie, G. I. 2005 Wave attractors and the asymptotic dissipation rate of tidal disturbances. J. Fluid Mech. 543, 19–44.CrossRefGoogle Scholar
Peat, K. S. 1978 Internal and inertial waves in a viscous rotating stratified fluid. Appl. Sci. Res. 33, 481–499.CrossRefGoogle Scholar
Proudman, I. 1956 The almost-rigid rotation of viscous fluid between concentric spheres. J. Fluid Mech. 1, 505–516.CrossRefGoogle Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.CrossRefGoogle Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.CrossRefGoogle Scholar
Roberts, P. H. & Stewartson, K. 1963 On the stability of a MacLaurin spheroid of small viscosity. Astrophys. J. 137, 777–790.CrossRefGoogle Scholar
St Laurent, L. & Garrett, C. 2002 The role of internal tides in mixing the deep ocean. J. Phys. Oceanogr. 32 (10), 2882–2899.2.0.CO;2>CrossRefGoogle Scholar
Stevenson, T. N., Bearon, J. N. & Thomas, N. H. 1974 An internal wave in a viscous heat-conducting isothermal atmosphere. J. Fluid Mech. 65, 315–323.CrossRefGoogle Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.CrossRefGoogle Scholar
Stewartson, K. 1966 On almost rigid rotations. Part 2. J. Fluid Mech. 26, 131–144.CrossRefGoogle Scholar
Thomas, N. H. & Stevenson, T. N. 1972 A similarity solution for viscous internal waves. J. Fluid Mech. 54, 495–506.CrossRefGoogle Scholar
Thomas, P. C., Tajeddine, R., Tiscareno, M. S., Burns, J. A., Joseph, J., Loredo, T. J., Helfenstein, P. & Porco, C. 2016 Enceladus’s measured physical libration requires a global subsurface ocean. Icarus 264, 37–47.CrossRefGoogle Scholar
Tilgner, A. 2000 Oscillatory shear layers in source driven flows in an unbounded rotating fluid. Phys. Fluids 12, 1101–1111.CrossRefGoogle Scholar
Voisin, B. 2003 Limit states of internal wave beams. J. Fluid Mech. 496, 243–293.CrossRefGoogle Scholar
van de Vooren, A. I. 1992 The Stewartson layer of a rotating disk of finite radius. J. Engng Maths 26, 131–152.CrossRefGoogle Scholar
Walton, I. C. 1975 On waves in a thin rotating spherical shell of slightly viscous fluid. Mathematika 22, 46–59.CrossRefGoogle Scholar
de Wijs, G. A., Kresse, G., Vocadlo, L., Dobson, D. et al. 1998 The viscosity of liquid iron at the physical conditions of the earth’s core. Nature 392 (6678), 805.CrossRefGoogle Scholar
Zhang, K., Chan, K. H., Liao, X. & Aurnou, J. M. 2013 The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration. J. Fluid Mech. 720, 212.CrossRefGoogle Scholar