Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wang, Qi
Xia, Shu-Ning
Wang, Bo-Fu
Sun, De-Jun
Zhou, Quan
and
Wan, Zhen-Hua
2018.
Flow reversals in two-dimensional thermal convection in tilted cells.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
355.
Wang, Qi
Wan, Zhen-Hua
Yan, Rui
and
Sun, De-Jun
2019.
Flow organization and heat transfer in two-dimensional tilted convection with aspect ratio 0.5.
Physics of Fluids,
Vol. 31,
Issue. 2,
Nandukumar, Yada
Chakraborty, Suman
Verma, Mahendra K.
and
Lakkaraju, Rajaram
2019.
On heat transport and energy partition in thermal convection with mixed boundary conditions.
Physics of Fluids,
Vol. 31,
Issue. 6,
Vasiliev, A.
Frick, P.
Kumar, A.
Stepanov, R.
Sukhanovskii, A.
and
Verma, M.K.
2019.
Transient flows and reorientations of large-scale convection in a cubic cell.
International Communications in Heat and Mass Transfer,
Vol. 108,
Issue. ,
p.
104319.
Castillo-Castellanos, Andrés
Sergent, Anne
Podvin, Bérengère
and
Rossi, Maurice
2019.
Cessation and reversals of large-scale structures in square Rayleigh–Bénard cells.
Journal of Fluid Mechanics,
Vol. 877,
Issue. ,
p.
922.
Foroozani, N.
Niemela, J. J.
Armenio, V.
and
Sreenivasan, K. R.
2019.
Turbulent convection and large scale circulation in a cube with rough horizontal surfaces.
Physical Review E,
Vol. 99,
Issue. 3,
Takeuchi, Shintaro
Miyamori, Yuri
Gu, Jingchen
and
Kajishima, Takeo
2019.
Flow reversals in particle-dispersed natural convection in a two-dimensional enclosed square domain.
Physical Review Fluids,
Vol. 4,
Issue. 8,
Faranda, D.
Podvin, B.
and
Sergent, A.
2019.
On reversals in 2D turbulent Rayleigh-Bénard convection: Insights from embedding theory and comparison with proper orthogonal decomposition analysis.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 29,
Issue. 3,
Soucasse, Laurent
Podvin, Bérengère
Rivière, Philippe
and
Soufiani, Anouar
2019.
Proper orthogonal decomposition analysis and modelling of large-scale flow reorientations in a cubic Rayleigh–Bénard cell.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
23.
Satbhai, Ojas
Roy, Subhransu
and
Ghosh, Sudipto
2019.
Direct Numerical Simulation of a Low Prandtl Number Rayleigh–Bénard Convection in a Square Box.
Journal of Thermal Science and Engineering Applications,
Vol. 11,
Issue. 6,
Chen, Xin
Wang, Dong-Pu
and
Xi, Heng-Dong
2020.
Reduced flow reversals in turbulent convection in the absence of corner vortices.
Journal of Fluid Mechanics,
Vol. 891,
Issue. ,
Kar, Prabir Kumar
Kumar, Yada Nandu
Das, P. K.
and
Lakkaraju, Rajaram
2020.
Thermal convection in octagonal-shaped enclosures.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Vishnu, Venugopal T.
De, Arnab K.
and
Mishra, Pankaj K.
2020.
Dynamics of large-scale circulation and energy transfer mechanism in turbulent Rayleigh–Bénard convection in a cubic cell.
Physics of Fluids,
Vol. 32,
Issue. 9,
Valori, Valentina
Innocenti, Alessio
Dubrulle, Bérengère
and
Chibbaro, Sergio
2020.
Weak formulation and scaling properties of energy fluxes in three-dimensional numerical turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Mommert, Michael
Schiepel, Daniel
Schmeling, Daniel
and
Wagner, Claus
2020.
Reversals of coherent structures in turbulent mixed convection.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Pritchard, Jesse R. J.
Chubynsky, Mykyta V.
Marston, Jeremy O.
and
Sprittles, James E.
2021.
Deformed liquid marble formation: Experiments and computational modeling.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Mandal, Sutapa
Ghosh, Manojit
Banerjee, Ankan
and
Pal, Pinaki
2021.
Dynamics of flow reversals in the presence of a vertical magnetic field
(a)
.
EPL (Europhysics Letters),
Vol. 135,
Issue. 5,
p.
54005.
Xu, Ao
Chen, Xin
and
Xi, Heng-Dong
2021.
Tristable flow states and reversal of the large-scale circulation in two-dimensional circular convection cells.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
van Hooft, J. Antoon
and
Popinet, Stéphane
2022.
A fourth-order accurate adaptive solver for incompressible flow problems.
Journal of Computational Physics,
Vol. 462,
Issue. ,
p.
111251.
Reiter, Philipp
Zhang, Xuan
and
Shishkina, Olga
2022.
Flow states and heat transport in Rayleigh–Bénard convection with different sidewall boundary conditions.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
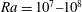 $Ra=10^{7}{-}10^{8}$ and Prandtl numbers
$Ra=10^{7}{-}10^{8}$ and Prandtl numbers  $Pr=3.0{-}4.3$ considered, two types of flow regimes are observed: a regime consisting of consecutive reversals, when the global rotation switches sign; and a regime consisting of an extended cessation, when global rotation is absent. A filtering method discriminates these two regimes and allows us to identify two characteristic time scales for the former regime. A time rescaling is then used to tune our records to a common duration, thus putting into evidence a generic reversal cycle. This cycle is composed of three successive phases: acceleration, accumulation and release including a rebound event. We complement this view in terms of a global angular impulse, available mechanical energy, global kinetic energy and their corresponding transfer rates. For a particular realisation of a reversal, each phase is described in terms of the flow patterns (large diagonal roll, counter-rotating corner flows and thermal plumes) and tied to the corresponding energy processes. We conclude by performing linear as well as nonlinear stability studies to account for the triggering mechanism of the release.
$Pr=3.0{-}4.3$ considered, two types of flow regimes are observed: a regime consisting of consecutive reversals, when the global rotation switches sign; and a regime consisting of an extended cessation, when global rotation is absent. A filtering method discriminates these two regimes and allows us to identify two characteristic time scales for the former regime. A time rescaling is then used to tune our records to a common duration, thus putting into evidence a generic reversal cycle. This cycle is composed of three successive phases: acceleration, accumulation and release including a rebound event. We complement this view in terms of a global angular impulse, available mechanical energy, global kinetic energy and their corresponding transfer rates. For a particular realisation of a reversal, each phase is described in terms of the flow patterns (large diagonal roll, counter-rotating corner flows and thermal plumes) and tied to the corresponding energy processes. We conclude by performing linear as well as nonlinear stability studies to account for the triggering mechanism of the release.




