Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-19T03:19:55.525Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of sub-Kolmogorov inertial particle pair dynamics in turbulence using novel satellite particle simulations

Published online by Cambridge University Press:  27 February 2013

Baidurja Ray  and
Lance R. Collins
Baidurja Ray
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14850, USA
Lance R. Collins*
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14850, USA
*
†Email address for correspondence: lc246@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Clustering (or preferential concentration) of weakly inertial particles suspended in a homogeneous isotropic turbulent flow is driven primarily by the smallest eddies at the so-called Kolmogorov scale. In particle-laden large-eddy simulations (LES), these small scales are not resolved by the grid and hence their effect on both the resolved flow scales and the particle motion have to be modelled. In order to predict clustering in a particle-laden LES, it is crucial that the subgrid model for the particles captures the mechanism by which the subgrid scales affect the particle motion (Ray & Collins, J. Fluid Mech., vol. 680, 2011, pp. 488–510). In this paper, we describe novel satellite particle simulations (SPS), in which we study the clustering and relative velocity statistics of inertial particles at separation distances well below the Kolmogorov length scale. SPS is designed to isolate pairwise interactions of particles, and is therefore well suited for developing two-particle models. We show that the power-law dependence of the radial distribution function (RDF), a statistical measure of clustering, is predicted by the SPS in excellent agreement with direct numerical simulations (DNS) for Stokes numbers up to 3, implying that no explicit information from the inertial range is required to accurately describe particle clustering. This result further explains our successful prediction of the RDF power using the drift-diffusion model of Chun et al. (J. Fluid Mech., vol. 536, 2005, pp. 219–251) for 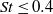$\mathit{St}\leq 0. 4$. We also consider the second-order longitudinal relative velocity structure function for the particles; we show that the SPS is able to capture its power-law exponent for 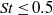$\mathit{St}\leq 0. 5$ and attribute the disagreement at larger 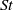$\mathit{St}$ to the effect of the larger scales of motion not captured by the SPS. Further, the SPS is able to capture the ‘caustic activation’ of the structure function at zero separation and predict the critical 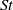$\mathit{St}$ and rate of activation in agreement with the DNS (Salazar & Collins, J. Fluid. Mech., vol. 696, 2012, pp. 45–66). We show comparisons between filtered DNS and equivalently filtered SPS, and the findings are similar to the unfiltered case. Overall, SPS is an efficient and accurate computational tool for investigating particle pair dynamics at small separations, as well as an interesting platform for developing LES subgrid models designed to accurately reproduce particle clustering.

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 192 - 211
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahluwalia, A. 2002 Preferential concentration of finite Stokes number particles in homogeneous isotropic turbulent flow. PhD thesis, Pennsylvania State University.Google Scholar
Ayala, O., Rosa, B. & Wang, L. P. 2008a Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10, 075016.Google Scholar
Ayala, O., Rosa, B., Wang, L. P. & Grabowski, W. W. 2008b Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 1. Results from direct numerical simulation. New J. Phys. 10, 075015.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A. S. & Toschi, F. 2010 Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.Google Scholar
Bini, M. & Jones, W. P. 2008 Large-eddy simulation of particle-laden turbulent flows. J. Fluid Mech. 614, 207–252.Google Scholar
Brucker, K. A., Isaza, J. C., Vaithianathan, T. & Collins, L. R. 2007 Efficient algorithm for simulating homogeneous turbulent shear flow without remeshing. J. Comput. Phys. 225, 20–32.Google Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97, 174501.Google Scholar
Chun, J., Koch, D. L., Rani, S., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Collins, L. R. & Keswani, A. 2004 Reynolds number scaling of particle clustering in turbulent aerosols. New J. Phys. 6, 119.Google Scholar
Devenish, B. J., Bartello, P., Brenguier, J.-L., Collins, L. R., Grabowski, W. W., IJzermans, R. H. A., Malinowski, S. P., Reeks, M. W., Vassilicos, J. C., Wang, L.-P. & Warhaft, Z. 2012 Droplet growth in warm turbulent clouds. Q. J. R. Meteorol. Soc. 138, 1401–1429.Google Scholar
Duncan, K., Mehlig, B., Östlund, S. & Wilkinson, M. 2005 Clustering by mixing flows. Phys. Rev. Lett. 95, 240602.Google Scholar
Eaton, J. K. & Fessler, J. R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.Google Scholar
Falkovich, G., Fouxon, A. & Stepanov, M. G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151–154.Google Scholar
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64, 4497.CrossRefGoogle Scholar
Fede, P. & Simonin, O. 2006 Numerical study of the subgrid fluid turbulence effects on the statistics of heavy colliding particles. Phys. Fluids 18, 045103.Google Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742–3749.Google Scholar
Gibert, M., Xu, H. & Bodenschatz, E. 2012 Where do small, weakly inertial particles go in a turbulent flow? J. Fluid Mech. 698, 160–167.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2012 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Hogan, R. C. & Cuzzi, J. N. 2001 Stokes and Reynolds number dependence of preferential particle concentration in simulated three-dimensional turbulence. Phys. Fluids 13, 2938–2945.Google Scholar
Ireland, P. J., Vaithianathan, T., Sukheswalla, P. S., Ray, B. & Collins, L. R. 2012 Highly parallel particle-laden flow solver for turbulence research. Comput. Fluids (in press).Google Scholar
Jin, G., He, G.-W. & Wang, L.-P. 2010 Large-eddy simulation of turbulent collision of heavy particles in isotropic turbulence. Phys. Fluids 22, 055106.Google Scholar
de Jong, J., Salazar, J. P. L. C., Cao, L., Woodward, S. H., Collins, L. R. & Meng, H. 2010 Measurement of inertial particle clustering and relative velocity statistics in isotropic turbulence using holographic imaging. Intl J. Multiphase Flow 36, 324–332.Google Scholar
Kerstein, A. R. & Krueger, S. K. 2006 Clustering of randomly advected low-inertia particles: a solvable model. Phys. Rev. E 73, 025302.Google Scholar
Kuerten, J. G. M. 2006 Subgrid modeling in particle-laden channel flow. Phys. Fluids 18 (2), 025108.Google Scholar
Marchioli, C., Salvetti, M. V. & Soldati, A. 2008 Some issues concerning large-eddy simulation of inertial particle dispersion in turbulent bounded flows. Phys. Fluids 20, 040603.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
McQuarrie, D. A. 1976 Statistical Mechanics. Harper & Row.Google Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73–107.Google Scholar
Patterson, G. S. & Orszag, S. A. 1971 Spectral calculation of isotropic turbulence: efficient removal of aliasing interactions. Phys. Fluids 14, 2538–2541.Google Scholar
Pinsky, M. B. & Khain, A. P. 1997 Turbulence effects on droplet growth and size distribution in clouds – a review. J. Aerosol Sci. 28, 1177–1214.CrossRefGoogle Scholar
Pozorski, J. & Apte, S. V. 2009 Filtered particle tracking in isotropic turbulence and stochastic modeling of subgrid-scale dispersion. Intl J. Multiphase Flow 35, 118–128.Google Scholar
Ray, B. & Collins, L. R. 2011 Preferential concentration and relative velocity statistics of inertial particles in Navier–Stokes turbulence with and without filtering. J. Fluid Mech. 680, 488–510.Google Scholar
Reade, W. C. & Collins, L. R. 2000a Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12, 2530–2540.Google Scholar
Reade, W. C. & Collins, L. R. 2000b A numerical study of the particle size distribution of an aerosol undergoing turbulent coagulation. J. Fluid Mech. 415, 45–64.Google Scholar
Salazar, J. P. L. C. & Collins, L. R. 2012 Inertial particle relative velocity statistics in homogeneous isotropic turbulence. J. Fluid Mech. 696, 45–66.Google Scholar
Salazar, J. P. L. C., de Jong, J., Cao, L., Woodward, S., Meng, H. & Collins, L. R. 2008 Experimental and numerical investigation of inertial particle clustering in isotropic turbulence. J. Fluid Mech. 600, 245–256.Google Scholar
Saw, E. W., Shaw, R. A., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100, 214501.Google Scholar
Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.Google Scholar
Shaw, R. A., Reade, W. C., Collins, L. R. & Verlinde, J. 1998 Preferential concentration of cloud droplets by turbulence: effects on the early evolution of cumulus cloud droplet spectra. J. Atmos. Sci. 55, 1965–1976.Google Scholar
Shotorban, B. & Mashayek, F. 2005 Modeling subgrid-scale effects on particles by approximate deconvolution. Phys. Fluids 17, 081701.Google Scholar
Shotorban, B. & Mashayek, F. 2006a On stochastic modeling of heavy particle dispersion in large-eddy simulation of two-phase turbulent flow. In IUTAM Symposium on Computational Multiphase Flow, pp. 373–380. Springer.Google Scholar
Shotorban, B. & Mashayek, F. 2006b A stochastic model for particle motion in large-eddy simulation. J. Turbul. 7, N11.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic, particle-laden turbulent suspension. Part I. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Sundaram, S. & Collins, L. R. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modeling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Wilkinson, M., Mehlig, B. & Bezuglyy, V. 2006 Caustic activation of rain showers. Phys. Rev. Lett. 97, 048501.Google Scholar
Witkowska, A., Brasseur, J. G. & Juvé, D. 1997 Numerical study of noise from isotropic turbulence. J. Comput. Acoust. 5, 317–336.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2007 Refinement of the probability density function model for preferential concentration of aerosol particles in isotropic turbulence. Phys. Fluids 19 (11), 113308.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.Google Scholar
Zemach, C. 1998 Appendix A: Mathematics of fluid mechanics. In The Handbook of Fluid Dynamics (ed. Johnson, R. W.). CRC Press.Google Scholar