No CrossRef data available.
Article contents
WAVE FRONT HOLONOMICITY OF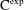 
$\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
Part of:
Algebraic number theory: local and $p$-adic fields
Number theory: Connections with logic
Birational geometry
Lie groups
Model theory
Published online by Cambridge University Press: 30 June 2020
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Many phenomena in geometry and analysis can be explained via the theory of 
$D$-modules, but this theory explains close to nothing in the non-archimedean case, by the absence of integration by parts. Hence there is a need to look for alternatives. A central example of a notion based on the theory of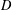 
$D$-modules is the notion of holonomic distributions. We study two recent alternatives of this notion in the context of distributions on non-archimedean local fields, namely 
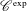$\mathscr{C}^{\text{exp}}$-class distributions from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] and WF-holonomicity from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We answer a question from Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)] by showing that each distribution of the 
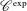$\mathscr{C}^{\text{exp}}$-class is WF-holonomic and thus provides a framework of WF-holonomic distributions, which is stable under taking Fourier transforms. This is interesting because the 
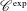$\mathscr{C}^{\text{exp}}$-class contains many natural distributions, in particular, the distributions studied by Aizenbud and Drinfeld [‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math.207(2) (2015), 527–580 (English)]. We show also another stability result of this class, namely, one can regularize distributions without leaving the 
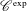$\mathscr{C}^{\text{exp}}$-class. We strengthen a link from Cluckers et al. [‘Distributions and wave front sets in the uniform nonarchimedean setting’, Trans. Lond. Math. Soc.5(1) (2018), 97–131] between zero loci and smooth loci for functions and distributions of the 
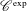$\mathscr{C}^{\text{exp}}$-class. A key ingredient is a new resolution result for subanalytic functions (by alterations), based on embedded resolution for analytic functions and model theory.
MSC classification
Primary:
14E18: Arcs and motivic integration
- Type
- Algebra
- Information
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Aizenbud, A. and Drinfeld, V., ‘The wave front set of the Fourier transform of algebraic measures’, Israel J. Math. 207(2) (2015), 527–580. (English).CrossRefGoogle Scholar
Bierstone, E. and Parusiński, A., ‘Global smoothing of a subanalytic set’, Duke Math. J. 167(16) (2018), 3115–3128.CrossRefGoogle Scholar
Bourbaki, N., Variétés Différentielles et Analytiques. Fascicule de Résultats (Hermann, Paris, 1967), (French).Google Scholar
Chambert-Loir, A., Nicaise, J. and Sebag, J., Motivic Integration, Progress in Mathematics, vol. 325, (Birkhäuser/Springer, New York, 2018).CrossRefGoogle Scholar
Cluckers, R., ‘Analytic p-adic cell decomposition and integrals’, Trans. Amer. Math. Soc. 356(4) (2004), 1489–1499.CrossRefGoogle Scholar
Cluckers, R., Comte, G. and Loeser, F., ‘Local metric properties and regular stratifications of p-adic definable sets’, Comment. Math. Helv. 87(4) (2012), 963–1009.CrossRefGoogle Scholar
Cluckers, R., Gordon, J. and Halupczok, I., ‘Integrability of oscillatory functions on local fields: transfer principles’, Duke Math. J. 163(8) (2014), 1549–1600.CrossRefGoogle Scholar
Cluckers, R., Gordon, J. and Halupczok, I., ‘Local integrability results in harmonic analysis on reductive groups in large positive characteristic’, Ann. Sci. Éc. Norm. Supér. (4) 47(6) (2014), 1163–1195.CrossRefGoogle Scholar
Cluckers, R., Gordon, J. and Halupczok, I., ‘Uniform analysis on local fields and applications to orbital integrals’, Trans. Amer. Math. Soc. Ser. B 5 (2018), 125–166.CrossRefGoogle Scholar
Cluckers, R. and Halupczok, I., ‘Integration of functions of motivic exponential class, uniform in all non-archimedean local fields of characteristic zero’, J. Ecole Polytechnique 5 (2018), 45–78.CrossRefGoogle Scholar
Cluckers, R., Halupczok, I., Loeser, F. and Raibaut, M., ‘Distributions and wave front sets in the uniform non-archimedean setting’, Trans. Lond. Math. Soc. 5(1) (2018), 97–131.CrossRefGoogle Scholar
Cluckers, R., Halupczok, I. and Rideau, S., ‘Hensel minimality’, Preprint, 2019,arXiv:1909.13792.Google Scholar
Cluckers, R. and Lipshitz, L., ‘Fields with analytic structure’, J. Eur. Math. Soc. (JEMS) 13 (2011), 1147–1223.CrossRefGoogle Scholar
Cluckers, R., Lipshitz, L. and Robinson, Z., ‘Analytic cell decomposition and analytic motivic integration’, Ann. Sci. Éc. Norm. Supér. (4) 39(4) (2006), 535–568.CrossRefGoogle Scholar
Cluckers, R. and Loeser, F., ‘Constructible exponential functions, motivic Fourier transform and transfer principle’, Ann. of Math. (2) 171 (2010), 1011–1065.CrossRefGoogle Scholar
Denef, J., ‘p-adic semialgebraic sets and cell decomposition’, J. reine angew. Math. 369 (1986), 154–166.Google Scholar
Denef, J., Report on Igusa’s local zeta function, Séminaire Bourbaki Vol. 1990/91, Exp. No. 730–744 (1991), 359–386, Astérisque 201–203.Google Scholar
Denef, J. and van den Dries, L., ‘p-adic and real subanalytic sets’, Ann. of Math. (2) 128(1) (1988), 79–138.CrossRefGoogle Scholar
Denef, J. and Loeser, F., ‘Motivic Igusa zeta functions’, J. Algebraic Geom. 7(3) (1998), 505–537.Google Scholar
Dieudonné, J. and Grothendieck, A., ‘Critères différentiels de régularité pour les localisés des algèbres analytiques’, J. Algebra 5 (1967), 305–324.CrossRefGoogle Scholar
van den Dries, L., ‘Dimension of definable sets, algebraic boundedness and Henselian fields’, Ann. Pure Appl. Logic 45 (1989), 189–209. Stability in model theory, II (Trento, 1987).CrossRefGoogle Scholar
van den Dries, L., Haskell, D. and Macpherson, D., ‘One-dimensional p-adic subanalytic sets’, J. Lond. Math. Soc. (2) 59(1) (1999), 1–20.CrossRefGoogle Scholar
van den Dries, L. and Scowcroft, P., ‘On the structure of semialgebraic sets over p-adic fields’, J. Symbolic Logic 53(4) (1988), 1138–1164.Google Scholar
Heifetz, D. B., ‘p-adic oscillatory integrals and wave front sets’, Pacific J. Math. 116(2) (1985), 285–305.CrossRefGoogle Scholar
Hironaka, H., ‘Resolution of singularities of an algebraic variety over a field of characteristic zero. I’, Ann. of Math. (2) 79(1) (1964), 109–203.CrossRefGoogle Scholar
Hörmander, L., ‘Fourier integral operators. I’, Acta Math. 127(1–2) (1971), 79–183.CrossRefGoogle Scholar
Igusa, J., An introduction to the theory of local zeta functions, Studies in Advanced Mathematics, (American Mathematical Society, Providence, RI; International Press, Cambridge, MA, 2000).Google Scholar
Loeser, F., ‘Trace formulas for motivic volumes’, Acta Math. Vietnam. 41(3) (2016), 409–424.CrossRefGoogle Scholar
Macintyre, A., ‘On definable subsets of p-adic fields’, J. Symbolic Logic 41 (1976), 605–610.CrossRefGoogle Scholar
Prestel, A. and Roquette, P., Formally p-adic Fields, Lecture Notes in Mathematics, vol. 1050. (Springer, Berlin, 1984).CrossRefGoogle Scholar
Raibaut, M., ‘Motivic wave front sets’, Int. Math. Res. Not. IMRN (2019), 36 pp. doi:10.1093/imrn/rnz196.Google Scholar
You have
Access
Open access