Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-20T10:32:49.034Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MULTI-MARGINAL OPTIMAL PARTIAL TRANSPORT PROBLEM

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  16 September 2015

JUN KITAGAWA  and
BRENDAN PASS
JUN KITAGAWA
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, Canada M5S 2E4; kitagawa@math.toronto.edu
BRENDAN PASS
Affiliation:
Department of Mathematical and Statistical Sciences, 632 CAB, University of Alberta, Edmonton, Alberta, Canada, T6G 2G1; pass@ualberta.ca

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce and study a multi-marginal optimal partial transport problem. Under a natural and sharp condition on the dominating marginals, we establish uniqueness of the optimal plan. Our strategy of proof establishes and exploits a connection with another novel problem, which we call the Monge–Kantorovich partial barycenter problem (with quadratic cost). This latter problem has a natural interpretation as a variant of the factories-and-mines description of optimal transport. We then turn our attention to various analytic properties of these two problems. Of particular interest, we show that monotonicity of the active marginals with respect to the amount 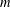$m$ of mass to be transported can fail, a surprising difference from the two-marginal case.

MSC classification

Primary: 35J96: Elliptic Monge-Ampère equations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e17
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Agueh, M. and Carlier, G., ‘Barycenters in the Wasserstein space’, SIAM J. Math. Anal. 43(2) (2011), 904–924.CrossRefGoogle Scholar
Brenier, Y., ‘Décomposition polaire et réarrangement monotone des champs de vecteurs’, C. R. Acad. Sci. Paris Sér. I 305(19) (1987), 805–808.Google Scholar
Brenier, Y., ‘Polar factorization and monotone rearrangement of vector-valued functions’, Commun. Pure Appl. Math. 44(4) (1991), 375–417.Google Scholar
Caffarelli, L. A., ‘The regularity of mappings with a convex potential’, J. Amer. Math. Soc. 5(1) (1992), 99–104.Google Scholar
Caffarelli, L. A., ‘Allocation maps with general cost functions’, inPartial Differential Equations and Applications, Lecture Notes in Pure and Applied Mathematics, 177 (Dekker, New York, 1996), 29–35.Google Scholar
Caffarelli, L. A. and McCann, R. J., ‘Free boundaries in optimal transport and Monge–Ampère obstacle problems’, Ann. of Math. (2) 171(2) (2010), 673–730.Google Scholar
Carlier, G., ‘On a class of multidimensional optimal transportation problems’, J. Convex Anal. 10(2) (2003), 517–529.Google Scholar
Carlier, G. and Ekeland, I., ‘Matching for teams’, Econom. Theory 42(2) (2010), 397–418.CrossRefGoogle Scholar
Carlier, G. and Nazaret, B., ‘Optimal transportation for the determinant’, ESAIM Control Optim. Calc. Var. 14(4) (2008), 678–698.CrossRefGoogle Scholar
Figalli, A., ‘The optimal partial transport problem’, Arch. Ration. Mech. Anal. 195(2) (2010), 533–560.Google Scholar
Gangbo, W., ‘Habilitation thesis’, Universite de Metz, available at http://people.math.gatech.edu/ gangbo/publications/habilitation.pdf, 1995.Google Scholar
Gangbo, W. and McCann, R. J., ‘The geometry of optimal transportation’, Acta Math. 177(2) (1996), 113–161.Google Scholar
Gangbo, W. and Świȩch, A., ‘Optimal maps for the multidimensional Monge–Kantorovich problem’, Commun. Pure Appl. Math. 51(1) (1998), 23–45.Google Scholar
Kim, Y.-H. and Pass, B., ‘A general condition for Monge solutions in the multi-marginal optimal transport problem’, SIAM J. Math. Anal. 46 (2014), 1538–1550.CrossRefGoogle Scholar
Knott, M. and Smith, C. S., ‘On a generalization of cyclic monotonicity and distances among random vectors’, Linear Algebra Appl. 199 (1994), 363–371.CrossRefGoogle Scholar
McCann, R. J., ‘Existence and uniqueness of monotone measure-preserving maps’, Duke Math. J. 80(2) (1995), 309–323.CrossRefGoogle Scholar
Olkin, I. and Rachev, S. T., ‘Maximum submatrix traces for positive definite matrices’, SIAM J. Matrix Anal. Appl. 14(2) (1993), 390–397.CrossRefGoogle Scholar
Pass, B., ‘Uniqueness and Monge solutions in the multi-marginal optimal transportation problem’, SIAM J. Math. Anal. 43(6) (2011), 2758–2775.Google Scholar
Pass, B., ‘On the local structure of optimal measures in the multi-marginal optimal transportation problem’, Calc. Var. Partial Differential Equations 43 (2012), 529–536. doi:10.1007/s00526-011-0421-z.Google Scholar
Pass, B., ‘Remarks on the semi-classical Hohenberg–Kohn functional’, Nonlinearity 26 (2013), 2731–2744.CrossRefGoogle Scholar
Pass, B., ‘Multi-marginal optimal transport and multi-agent matching problems: uniqueness and structure of solutions’, Discrete Contin. Dyn. Syst. 34 (2014), 1623–1639.Google Scholar