No CrossRef data available.
Article contents
Critical values for the 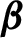 $\boldsymbol{\beta} $-transformation with a hole at
$\boldsymbol{\beta} $-transformation with a hole at 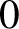 $0$
$0$
Published online by Cambridge University Press: 02 May 2022
Abstract
Given
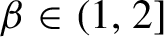 $\beta \in (1,2]$
, let
$\beta \in (1,2]$
, let
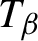 $T_{\beta }$
be the
$T_{\beta }$
be the
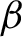 $\beta $
-transformation on the unit circle
$\beta $
-transformation on the unit circle
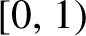 $[0,1)$
such that
$[0,1)$
such that
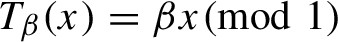 $T_{\beta }(x)=\beta x\pmod 1$
. For each
$T_{\beta }(x)=\beta x\pmod 1$
. For each
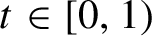 $t\in [0,1)$
, let
$t\in [0,1)$
, let
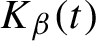 $K_{\beta }(t)$
be the survivor set consisting of all
$K_{\beta }(t)$
be the survivor set consisting of all
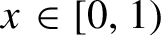 $x\in [0,1)$
whose orbit
$x\in [0,1)$
whose orbit
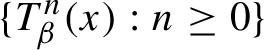 $\{T^{n}_{\beta }(x): n\ge 0\}$
never hits the open interval
$\{T^{n}_{\beta }(x): n\ge 0\}$
never hits the open interval
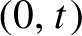 $(0,t)$
. Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020) 2482–2514] proved that the Hausdorff dimension function
$(0,t)$
. Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020) 2482–2514] proved that the Hausdorff dimension function
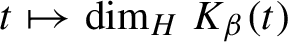 $t\mapsto \dim _{H} K_{\beta }(t)$
is a non-increasing Devil’s staircase. So there exists a critical value
$t\mapsto \dim _{H} K_{\beta }(t)$
is a non-increasing Devil’s staircase. So there exists a critical value
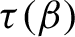 $\tau (\beta )$
such that
$\tau (\beta )$
such that
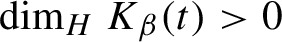 $\dim _{H} K_{\beta }(t)>0$
if and only if
$\dim _{H} K_{\beta }(t)>0$
if and only if
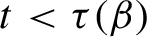 $t<\tau (\beta )$
. In this paper, we determine the critical value
$t<\tau (\beta )$
. In this paper, we determine the critical value
 $\tau (\beta )$
for all
$\tau (\beta )$
for all
 $\beta \in (1,2]$
, answering a question of Kalle et al (2020). For example, we find that for the Komornik–Loreti constant
$\beta \in (1,2]$
, answering a question of Kalle et al (2020). For example, we find that for the Komornik–Loreti constant
 $\beta \approx 1.78723$
, we have
$\beta \approx 1.78723$
, we have
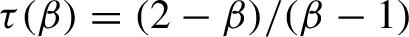 $\tau (\beta )=(2-\beta )/(\beta -1)$
. Furthermore, we show that (i) the function
$\tau (\beta )=(2-\beta )/(\beta -1)$
. Furthermore, we show that (i) the function
 $\tau : \beta \mapsto \tau (\beta )$
is left continuous on
$\tau : \beta \mapsto \tau (\beta )$
is left continuous on
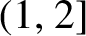 $(1,2]$
with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii)
$(1,2]$
with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii)
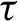 $\tau $
has no downward jumps, with
$\tau $
has no downward jumps, with
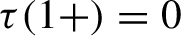 $\tau (1+)=0$
and
$\tau (1+)=0$
and
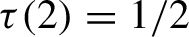 $\tau (2)=1/2$
; and (iii) there exists an open set
$\tau (2)=1/2$
; and (iii) there exists an open set
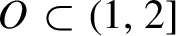 $O\subset (1,2]$
, whose complement
$O\subset (1,2]$
, whose complement
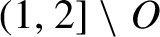 $(1,2]\setminus O$
has zero Hausdorff dimension, such that
$(1,2]\setminus O$
has zero Hausdorff dimension, such that
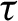 $\tau $
is real-analytic, convex, and strictly decreasing on each connected component of O. Consequently, the dimension
$\tau $
is real-analytic, convex, and strictly decreasing on each connected component of O. Consequently, the dimension
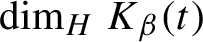 $\dim _{H} K_{\beta }(t)$
is not jointly continuous in
$\dim _{H} K_{\beta }(t)$
is not jointly continuous in
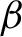 $\beta $
and t. Our strategy to find the critical value
$\beta $
and t. Our strategy to find the critical value
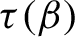 $\tau (\beta )$
depends on certain substitutions of Farey words and a renormalization scheme from dynamical systems.
$\tau (\beta )$
depends on certain substitutions of Farey words and a renormalization scheme from dynamical systems.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press





