Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T05:51:36.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity and non-recurrence along sequences

Published online by Cambridge University Press:  16 April 2013

V. BERGELSON ,
A. DEL JUNCO ,
M. LEMAŃCZYK  and
J. ROSENBLATT
V. BERGELSON
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA email vitaly@math.ohio-state.edu
A. DEL JUNCO
Affiliation:
Department of Mathematics, University of Toronto, Toronto, M5S 3G3, Canada email deljunco@math.toronto.edu
M. LEMAŃCZYK
Affiliation:
Faculty of Math and Computer Science, Nicolaus Copernicus University, Toruń, Poland email mlem@mat.uni.torun.pl
J. ROSENBLATT
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA email rosnbltt@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

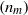We study two properties of a finite measure-preserving dynamical system and a given sequence $({n}_{m} )$ of positive integers, namely rigidity and non-recurrence. Our goal is to find conditions on the sequence which ensure that it is, or is not, a rigid sequence or a non-recurrent sequence for some weakly mixing system or more generally for some ergodic system. The main focus is on weakly mixing systems. For example, we show that for any integer 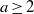$a\geq 2$ the sequence 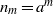${n}_{m} = {a}^{m} $ is a sequence of rigidity for some weakly mixing system. We show the same for the sequence of denominators of the convergents in the continued fraction expansion of any irrational $\alpha $. We also consider the stronger property of IP-rigidity. We show that if 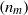$({n}_{m} )$ grows fast enough then there is a weakly mixing system which is IP-rigid along $({n}_{m} )$ and non-recurrent along 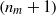$({n}_{m} + 1)$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 5 , October 2014 , pp. 1464 - 1502
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. Rational ergodicity, bounded rational ergodicity, and some continuous measures on the circle. Israel J. Math. 33 (3–4) (1979), 181–197.CrossRefGoogle Scholar
Aaronson, J., Hosseini, M. and Lemańczyk, M.. IP-rigidity and eigenvalue groups. Ergod. Th. & Dynam. Sys. to appear. Preprint, 23 pp.Google Scholar
Aaronson, J., Lemańczyk, M., Mauduit, C. and Nakada, H.. Koksma inequality and group extensions of Kronecker transformations. Algorithms, Fractals and Dynamics. Ed. Takahashi, Y.. Plenum Press, New York, 1995, pp. 27–50.Google Scholar
Adams, T.. Tower multiplexing and slow weak mixing. Preprint, 22 pp.Google Scholar
Ajtai, M., Havas, I. and Komlós, J.. Every Group Admits a Bad Topology (Studies in Pure Mathematics). Birkhäuser, Basel, 1983, pp. 21–34.Google Scholar
Bergelson, V.. Ergodic Ramsey Theory: An Update. Ergodic Theory of Z d Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228). Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, V.. Combinatorial and diophantine applications of ergodic theory. Appendix A by A. Leibman and Appendix B by A. Quas and M. Wierdl. Handbook of Dynamical Systems. Vol. 1B. Elsevier B. V., Amsterdam, 2006, pp. 745–869.Google Scholar
Bergelson, V. and Håland, I.. Weak mixing implies mixing of higher orders along tempered functions. Ergod. Th. & Dynam. Sys. 29 (2009), 1375–1416.Google Scholar
Chacón, R. V.. Weakly mixing transformations which are not strongly mixing. Proc. Amer. Math. Soc. 22 (1969), 559–562.CrossRefGoogle Scholar
Cornfeld, I. P., Fomin, S. V. and Sinai, Ya. G.. Ergodic Theory. Springer, Berlin, 1982.Google Scholar
Derriennic, Y., Fraczek, K., Lemańczyk, M. and Parreau, F.. Ergodic automorphisms whose weak closure of off-diagonal measures consists of ergodic self-joinings. Colloq. Math. 110 (2008), 81–115.Google Scholar
Eisner, T. and Grivaux, S.. Hilbertian Jamison sequences and rigid dynamical systems. Preprint, 36 pages.Google Scholar
Eggleston, H. G.. Sets of fractional dimensions which occur in some problems of number theory. Proc. Lond. Math. Soc. (2) 54 (1952), 42–93.Google Scholar
Erdős, P. and Taylor, S. J.. On the set of points of convergence of a lacunary trigonometric series and the equidistribution properties of related sequences. Proc. Lond. Math. Soc. (3) 7 (1957), 598–615.Google Scholar
Fayad, B.. Weak mixing for reparameterized linear flows on the torus. Ergod. Th. & Dynam. Sys. 22 (1) (2002), 187–201.CrossRefGoogle Scholar
Ferenczi, S.. Systems of finite rank. Colloq. Math. 73 (1997), 36–65.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.CrossRefGoogle Scholar
Furstenberg, H.. Poincaré recurrence and number theory. Bull. Amer. Math. Soc. 5 (3) (1981), 211–234.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. The finite multipliers of infinite ergodic transformations. The Structure of Attractors in Dynamical Systems (Proc. Conf. North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668). Springer, Berlin, 1978, pp. 127–132.Google Scholar
Hahn, F. and Parry, W.. Some characteristic properties of dynamical systems with quasi-discrete spectrum. Math. Syst. Theory 2 (1968), 179–190.CrossRefGoogle Scholar
Halmos, P.. Lectures on Ergodic Theory. Chelsea Publishing Co., New York, 1960.Google Scholar
Helson, H.. Cocycles on the circle. J. Operator Theory 16 (1986), 189–199.Google Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–234.Google Scholar
Herman, M.. ${L}_{2} $ regularity of measurable solutions of a finite difference equation of the circle. Ergod. Th. & Dynam. Sys. 24 (5) (2004), 1277–1281.Google Scholar
Iwanik, A., Lemańczyk, M. and Rudolph, D.. Absolutely continuous cocycles over irrational rotations. Israel J. Math. 83 (1993), 73–95.Google Scholar
Katznelson, Y.. An Introduction to Harmonic Analysis. John Wiley & Sons, New York, 1968.Google Scholar
Katok, A. and Stepin, A.. Approximations in ergodic theory. Uspekhi Mat. Nauk 22 (5(137)) (1967), 81–106; Engl. Transl. Russian Math. Surveys 22(5) (1967), 77–102.Google Scholar
Kingman, J. F. C.. Poisson Processes (Oxford Studies in Probability, 3). Clarendon Press, Oxford, 1993.Google Scholar
Kra, B.. Poincaré recurrence and number theory: thirty years later [comment on the reprint of MR0628658]. Bull. Amer. Math. Soc. (N.S.) 48 (4) (2011), 497–501.Google Scholar
Krzyżewski, K.. On regularity of measurable solutions of a cohomology equations. Bull. Pol. Acad. Sci. Math. 37 (1989), 279–287.Google Scholar
Krieger, W.. On entropy and generators of measure-preserving transformations. Trans. Amer. Math. Soc. 149 (1970), 453–464.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences (Pure and Applied Mathematics). Wiley-Interscience, John Wiley & Sons, New York, 1974.Google Scholar
Kwiatkowski, J., Lemańczyk, M. and Rudolph, D.. A class of real cocycles having an analytic coboundary modification. Israel J. Math. 87 (1994), 337–360.CrossRefGoogle Scholar
LaFontaine, J.. Réunions d’emsembles lacunaires. Contributions á la théorie des séries trig. et á la théorie des nombres (Bulletin Societé Mathématique France, Memoire 19). Ed. Kahane, J.-P.. Societé Mathématique de France, Paris, 1969, pp. 21–25.Google Scholar
Lemańczyk, M. and Lesigne, E.. Ergodicity of Rokhlin cocycles. J. Anal. Math. 85 (2001), 43–86.CrossRefGoogle Scholar
Lemańczyk, M. and Parreau, F.. Rokhlin extensions and lifting disjointness. Ergod. Th. & Dynam. Sys. 23 (2003), 1525–1550.Google Scholar
Liardet, P. and Volný, D.. Sums of continuous and differentiable functions in dynamical systems. Israel J. Math. 98 (1997), 29–60.Google Scholar
de Mathan, B.. Sur un problème de densité modulo 1. C. R. Acad. Sci. Paris Sér. A-B (5) (1978), A277–A279.Google Scholar
Moore, C. C. and Schmidt, K.. Coboundaries and homomorphisms for non-singular actions and a problem of H. Helson. Proc. Lond. Math. Soc. (3) 40 (1980), 443–475.Google Scholar
Nadkarni, M. G.. Spectral Theory of Dynamical Systems (Birkhäuser Advanced Texts). Birkhäuser, Basel, 1998.Google Scholar
Neretin, Yu. A.. Categories of Symmetries and Infinite-Dimensional Groups. Clarendon Press, Oxford, 1996.Google Scholar
Parry, W.. Topics in Ergodic Theory (Cambridge Tracts in Mathematics, 75). Cambridge University Press, Cambridge, 1981.Google Scholar
Pollington, A.. On the density of sequence $(\{ {n}_{k} \xi \} )$. Illinois J. Math. 23 (4) (1979), 511–515.Google Scholar
Ramaré, O.. On Shnirelman’s constant. Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 22 (4) (1995), 645–706.Google Scholar
Rhin, G.. Sur la repartition modulo 1 des suites $f(p)$. Acta Arith. 23 (1973), 217–248.Google Scholar
de la Rue, T.. Rang des systèmes dynamiques Gaussiens. Israel J. Math. 104 (1998), 261–283.Google Scholar
Rosenblatt, J.. Norm convergence in ergodic theory and the behavior of Fourier transforms. Canad. J. Math. 46 (1994), 184–199.Google Scholar
Roy, E.. Poisson suspensions and infinite ergodic theory. Ergod. Th. & Dynam. Sys. 29 (2009), 667–683.Google Scholar
Rudin, W.. Fourier Analysis on Groups (Interscience Tracts in Pure and Applied Mathematics, 12). Interscience Publishers, John Wiley & Sons, New York, 1962.Google Scholar
Rudin, W.. Independent perfect sets in groups. Michigan Math. J. 5 (2) (1958), 159–161.Google Scholar
Salem, R.. The absoute convergence of trigonometrical series. Oeuvres Mathématiques. Hermann, Paris, 1967, pp. 201–218.Google Scholar
Salem, R.. On some properties of symmetrical perfect sets. Oeuvres Mathématiques. Hermann, Paris, 1967, pp. 219–227.Google Scholar
Sierpiński, W.. General Topology, 2nd edn. University of Toronto Press, Toronto, 1956.Google Scholar
Walters, P.. Some invariant $\sigma $-algebras for measure-preserving transformations. Trans. Amer. Math. Soc. 163 (1972), 357–368.Google Scholar