Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T22:19:22.167Z Has data issue: false hasContentIssue false
  • English
  • Français

Bernstein and Jackson theorems for the Heisenberg group

Part of: Approximations and expansions Abstract harmonic analysis

Published online by Cambridge University Press:  09 April 2009

Saverio Giulini
Saverio Giulini
Affiliation:
Dipartimento di Matematica Università di MilanoVia Saldini 50 20133 Milano, Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe on the Heisenberg group Hn a family of spaces M(h, X) of functions which play a role analogous to the trigonometric polynomials in Tn or the functions of exponential type in Rn. In particular we prove that for the space M(h, X), Jackson's theorem holds in the classical form while Bernstein's inequality hold in a modified form. We end of the paper with a characterization of the functions of the Lipschitz space 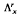by the behavior of their best approximations by functions in the space M(h, X).

MSC classification

Secondary: 41A17: Inequalities in approximation (Bernstein, Jackson, Nikol'skiĭ-type inequalities) 43A80: Analysis on other specific Lie groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 38 , Issue 2 , April 1985 , pp. 241 - 254
Copyright
Copyright © Australian Mathematical Society 1985

References

[1]Cartwright, D. I. and Soardi, P. M., ‘Best conditions for the norm convergence of Fourier series’, J. Approx. Theory 38 (1983), 344–353.CrossRefGoogle Scholar
[2]Cygan, J., ‘Subadditivity of homogeneous norms on certain nilpotent Lie group’, Proc. Amer. Math. Soc. 83 (1981), 69–70.Google Scholar
[3]Folland, G. B. and Stein, E. M., Hardy spaces on homogeneous groups (Mathematical Notes 28, Princeton Univ. Press, Princeton, N. J., 1982).Google Scholar
[4]Geller, D., ‘Fourier analysis on the Heisenberg group’, Proc. Nat. Acad. Sci. U.S.A. 74 (1977), 1328–1331.CrossRefGoogle ScholarPubMed
[5]Geller, D., ‘Local solvability and homogeneous distributions on the Heisenberg group’, Comm. Partial Differential Equations 5 (1980), 475–560.Google Scholar
[6]Inglis, I. R., ‘Bernstein's theorem and the Fourier algebra of the Heisenberg group’, Boll. Un. Mat. It., to appear.Google Scholar
[7]Soardi, P. M., ‘On non-isotropic Lipschitz spaces’, Harmonic analysis (Lecture Notes in Math. 992, Springer-Verlag, Berlin, 1983).Google Scholar