Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-24T01:44:48.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalizations of Deissler's Minimality Rank1

Published online by Cambridge University Press:  12 March 2014

T. G. Kucera
T. G. Kucera*
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, Ontario P7B 5E1, Canada
*
Department of Mathematics and Astronomy, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

This is the first of two papers based on Chapter V of the author's Ph.D. thesis [K1]. The second paper [K3] will deal with a specific application of the ideas presented here to the study of modules, mostly to questions concerning the complexity of injective modules over a commutative Noetherian ring.

In [D], R. Deissler introduced a “minimality rank” which I denote by “rk” here. This rank provides an ordinal measure on the difficulty of defining a given element b in a structure ℳ, allowing the use of parameters from definable subsets of ℳ. If A ⊂ M, rk(b, A, ℳ) = 0 if b is definable in ℳ by a formula with parameters from A. Roughly speaking, in the general case rk(b, A, ℳ) measures how hard we have to work at adding new parameters to A (from sets definable over A in ℳ) in order to be able to define b. “rk” is called a “minimality rank” because of the following: ℳ is a minimal model of the complete theory T = Th(ℳ) iff rk(b, Ø, ℳ) < ∞ for every b ∈ M. Deissler's rank was studied further by R. Woodrow and J. Knight [WK]. They improve on an example given by Deissler. The construction that they present illustrates well the difficulties and subtleties involved in exact calculations of rk.

The central concept underlying Deissler's rank is that of a definable set. In §1 I introduce the idea of a context for definability Φ(x). A set B is Φ-definable over A if for some formula and 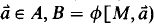. For Deissler's rank, Φ is the set of all formulas; for rk+ used in the study of modules, Φ + is the set of all positive primitive formulas. Associated with each Φ is a relation ≺Φ between structures which says that Φ-definitions are preserved. In §1 I develop the basic properties of these two concepts and give a list of examples.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 1 , March 1988 , pp. 269 - 283
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper is based on Chapter V of my doctoral dissertation [Kl] prepared under the direction of Dr. M. Makkai at McGill University. I would like to thank Dr. Makkai for his patient and stimulating guidance. I would also like to acknowledge the financial support received through scholarships and grants from the Natural Sciences and Engineering Research Council of Canada (NSERC) and through FCAC Québec. I would also like to thank Dr. R. Woodrow for discussing an early version of these results with me. This paper was prepared while I was employed at the University of Saskatchewan. I would like to thank the Department of Mathematics for its support. I would also like to thank the referee for a most careful reading of the manuscript to this paper and its sequel, and for suggesting several improvements in their presentation.

References

REFERENCES

[B] Baldwin, J. T., αT is finite for ℵ1-categorical T, Transactions of the American Mathematical Societ, vol. 181 (1973), pp. 37–51.Google Scholar
[Ba] Baur, W., Elimination of quantifiers for modules, Israel Journal of Mathematics, vol. 25(1976), pp. 64–70.Google Scholar
[Bo] Bouscaren, E., Existentially closed modules: types and prime models, Model theory of algebra and arithmetic (Pacholski, L. et al., editors), Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 31–43.CrossRefGoogle Scholar
[CK] Chang, C. C. and J. Keisler, H., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[D] Deissler, R., Minimal models, this Journal, vol. 42 (1977), pp. 254–260.Google Scholar
[ES] Eklof, P. and Sabbagh, G., Model completions and modules, Annals of Mathematical Logic, vol. 2 (1971), pp. 251–295.CrossRefGoogle Scholar
[HH] Harnik, V. and Harrington, L., Fundamentals of forking, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 245–286.Google Scholar
[Kl] Kucera, T. G., Applications of stability-theoretical methods to theories of modules, Ph.D. thesis, McGill University, Montréal, 1984.Google Scholar
[K2] Kucera, T. G., Totally transcendental theories of modules: decomposition of models and types, Annals of Pure and Applied Logic (to appear).Google Scholar
[K3] Kucera, T. G., Positive Deissler rank and the complexity of injective modules, this Journal, vol. 53 (1988), pp. 284–293.Google Scholar
[L] Lascar, D., Ordre de Rudin-Keisler et poids dans les théories stables, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 28 (1982), pp. 413–430.CrossRefGoogle Scholar
[LP] Lascar, D. and Poizat, B., Introduction to forking, this Journal, vol. 44 (1979), pp. 330–350.Google Scholar
[M] Makkai, M., A survey of basic stability theory, with particular emphasis on orthogonality and regular types, Israel Journal of Mathematics, vol. 49 (1984), pp. 181–238.CrossRefGoogle Scholar
[Mo] Monk, L., Elementary-recursive decision procedures, Ph.D. thesis, University of California, Berkeley, California, 1975.Google Scholar
[Sh] Shelah, S., Classification theory and the number of non-isomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[Sm 1] Smith, K. W., Stability of lattices, Ph.D. thesis, University of Toronto, Toronto, 1979.Google Scholar
[Sm 2] Smith, K. W., Stability and categoricity of lattices, Canadian Journal of Mathematics, vol. 33 (1981), pp. 1380–1419.CrossRefGoogle Scholar
[WK] Woodrow, R. E. and Knight, J., A complete theory with arbitrarily large minimality ranks, this Journal, vol. 48 (1983), pp. 321–328.Google Scholar
[Z] Ziegler, M., Model theory of modules, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 149–213.CrossRefGoogle Scholar