Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cai, Jun
and
Tang, Qihe
2004.
On max-sum equivalence and convolution closure of heavy-tailed distributions and their applications.
Journal of Applied Probability,
Vol. 41,
Issue. 01,
p.
117.
Tang, Qihe
2004.
Asymptotics for the Finite Time Ruin Probability in the Renewal Model with Consistent Variation.
Stochastic Models,
Vol. 20,
Issue. 3,
p.
281.
Kaas, Rob
and
Tang, Qihe
2005.
A large deviation result for aggregate claims with dependent claim occurrences.
Insurance: Mathematics and Economics,
Vol. 36,
Issue. 3,
p.
251.
Wang, Yue Bao
Wang, Kai Yong
and
Cheng, Dong Ya
2006.
Precise Large Deviations for Sums of Negatively Associated Random Variables with Common Dominatedly Varying Tails.
Acta Mathematica Sinica, English Series,
Vol. 22,
Issue. 6,
p.
1725.
Liu, Yan
2007.
Precise large deviations for negatively associated random variables with consistently varying tails.
Statistics & Probability Letters,
Vol. 77,
Issue. 2,
p.
181.
Wang, Shijie
and
Wang, Wensheng
2007.
Precise Large Deviations for Sums of Random Variables with Consistently Varying Tails in Multi-Risk Models.
Journal of Applied Probability,
Vol. 44,
Issue. 04,
p.
889.
Chen, Yu
and
Zhang, Weiping
2007.
Large deviations for random sums of negatively dependent random variables with consistently varying tails.
Statistics & Probability Letters,
Vol. 77,
Issue. 5,
p.
530.
Baltrūnas, Aleksandras
Leipus, Remigijus
and
Šiaulys, Jonas
2008.
Precise large deviation results for the total claim amount under subexponential claim sizes.
Statistics & Probability Letters,
Vol. 78,
Issue. 10,
p.
1206.
Aleškevičienė, Aldona
Leipus, Remigijus
and
Šiaulys, Jonas
2008.
Tail behavior of random sums under consistent variation with applications to the compound renewal risk model.
Extremes,
Vol. 11,
Issue. 3,
p.
261.
Shen, Xinmei
and
Lin, Zhengyan
2008.
Precise large deviations for randomly weighted sums of negatively dependent random variables with consistently varying tails.
Statistics & Probability Letters,
Vol. 78,
Issue. 18,
p.
3222.
Lin, Jianxi
2008.
Some Blackwell-Type Renewal Theorems for Weighted Renewal Functions.
Journal of Applied Probability,
Vol. 45,
Issue. 04,
p.
972.
Jiang, Tao
2008.
Large-deviation probabilities for maxima of sums of subexponential random variables with application to finite-time ruin probabilities.
Science in China Series A: Mathematics,
Vol. 51,
Issue. 7,
p.
1257.
Lin, Jianxi
2008.
The general principle for precise large deviations of heavy-tailed random sums.
Statistics & Probability Letters,
Vol. 78,
Issue. 6,
p.
749.
Denisov, D.
Dieker, A. B.
and
Shneer, V.
2008.
Large deviations for random walks under subexponentiality: The big-jump domain.
The Annals of Probability,
Vol. 36,
Issue. 5,
Robert, Christian Y.
and
Segers, Johan
2008.
Tails of random sums of a heavy-tailed number of light-tailed terms.
Insurance: Mathematics and Economics,
Vol. 43,
Issue. 1,
p.
85.
Shen, Xin-Mei
Lin, Zheng-Yan
and
Zhang, Yi
2009.
Precise Large Deviations for the Actual Aggregate Loss Process.
Stochastic Analysis and Applications,
Vol. 27,
Issue. 5,
p.
1000.
Chen, Yiqing
and
Yuen, Kam C.
2009.
Sums of Pairwise Quasi-Asymptotically Independent Random Variables with Consistent Variation.
Stochastic Models,
Vol. 25,
Issue. 1,
p.
76.
Liu, Li
2009.
Precise large deviations for dependent random variables with heavy tails.
Statistics & Probability Letters,
Vol. 79,
Issue. 9,
p.
1290.
Liu, Li
2010.
Necessary and sufficient conditions for moderate deviations of dependent random variables with heavy tails.
Science China Mathematics,
Vol. 53,
Issue. 6,
p.
1421.
Yang, Yang
Leipus, Remigijus
and
Šiaulys, Jonas
2010.
Local precise large deviations for sums of random variables with -regularly varying densities.
Statistics & Probability Letters,
Vol. 80,
Issue. 19-20,
p.
1559.
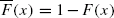 is consistently varying as x tends to infinity, this paper investigates precise large deviations for both the partial sums S
n
and the random sums S
N(t), where N(·) is a counting process independent of the sequence {X
k
, k ≥ 1}. The obtained results improve some related classical ones. Applications to a risk model with negatively associated claim occurrences and to a risk model with a doubly stochastic arrival process (extended Cox process) are proposed.
is consistently varying as x tends to infinity, this paper investigates precise large deviations for both the partial sums S
n
and the random sums S
N(t), where N(·) is a counting process independent of the sequence {X
k
, k ≥ 1}. The obtained results improve some related classical ones. Applications to a risk model with negatively associated claim occurrences and to a risk model with a doubly stochastic arrival process (extended Cox process) are proposed.



