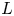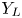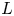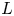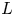1. Introduction
Given a closed, oriented manifold $N$![]() of odd dimension, together with a representation $\alpha \colon \pi _1(N)\to U(n)$
of odd dimension, together with a representation $\alpha \colon \pi _1(N)\to U(n)$![]() for some $n\in \mathbb {N}$
for some $n\in \mathbb {N}$![]() , we can consider the Atiyah–Patodi–Singer rho invariant $\rho _\alpha (N)$
, we can consider the Atiyah–Patodi–Singer rho invariant $\rho _\alpha (N)$![]() . This is a real number defined as the difference between the eta invariant of the twisted and the untwisted odd signature operator associated with any Riemannian metric on $N$
. This is a real number defined as the difference between the eta invariant of the twisted and the untwisted odd signature operator associated with any Riemannian metric on $N$![]() , and it turns out to be independent of the choice of the metric [Reference Atiyah, Patodi and Singer1, Reference Atiyah, Patodi and Singer2]. The rho invariant is thus defined as a spectral invariant, but it has the following fundamental property that relates it to well-studied topological invariants: if $N$
, and it turns out to be independent of the choice of the metric [Reference Atiyah, Patodi and Singer1, Reference Atiyah, Patodi and Singer2]. The rho invariant is thus defined as a spectral invariant, but it has the following fundamental property that relates it to well-studied topological invariants: if $N$![]() is the boundary of a compact, oriented manifold $M$
is the boundary of a compact, oriented manifold $M$![]() such that the representation $\alpha$
such that the representation $\alpha$![]() extends to $\pi _1(M)$
extends to $\pi _1(M)$![]() , then it can be computed as
, then it can be computed as
where $\sigma (M)$![]() denotes the ordinary signature of $M$
denotes the ordinary signature of $M$![]() , and $\sigma _\alpha (M)$
, and $\sigma _\alpha (M)$![]() is the twisted signature associated with the chosen extension $\alpha \colon \pi _1(M)\to U(n)$
is the twisted signature associated with the chosen extension $\alpha \colon \pi _1(M)\to U(n)$![]() .
.
In knot theory, rho invariants are used to give descriptions and generalizations of knot and link signatures. One of the basic observations is that, if $S_K$![]() is the closed manifold obtained by $0$
is the closed manifold obtained by $0$![]() -framed surgery on $K$
-framed surgery on $K$![]() and $\alpha \colon \pi _1(S_K)\to U(1)$
and $\alpha \colon \pi _1(S_K)\to U(1)$![]() is the representation sending the meridian of $K$
is the representation sending the meridian of $K$![]() to $\omega \in U(1)$
to $\omega \in U(1)$![]() , then
, then
where $\sigma _K$![]() is the Levine–Tristram signature function of $K$
is the Levine–Tristram signature function of $K$![]() . Atiyah–Patodi–Singer rho invariants associated with higher-dimensional non-abelian representations were used in the knot theory by Levine [Reference Levine22, Reference Levine23] and Friedl [Reference Friedl16, Reference Friedl17] as obstructions to knot and link concordance. Multivariable signatures of links, defined by Cimasoni and Florens [Reference Cimasoni and Florens9] using generalized Seifert surfaces, were given a description as twisted signatures of four manifolds and also employed as concordance invariants [Reference Cimasoni and Florens9, Reference Conway, Nagel and Toffoli12, Reference Degtyarev, Florens and Lecuona13]. However, a description of them as Atiyah–Patodi–Singer rho invariants was not investigated thoroughly. One of the goals of this paper is to fill this gap.
. Atiyah–Patodi–Singer rho invariants associated with higher-dimensional non-abelian representations were used in the knot theory by Levine [Reference Levine22, Reference Levine23] and Friedl [Reference Friedl16, Reference Friedl17] as obstructions to knot and link concordance. Multivariable signatures of links, defined by Cimasoni and Florens [Reference Cimasoni and Florens9] using generalized Seifert surfaces, were given a description as twisted signatures of four manifolds and also employed as concordance invariants [Reference Cimasoni and Florens9, Reference Conway, Nagel and Toffoli12, Reference Degtyarev, Florens and Lecuona13]. However, a description of them as Atiyah–Patodi–Singer rho invariants was not investigated thoroughly. One of the goals of this paper is to fill this gap.
Given the difficulty in computing rho invariants directly, it can be very useful to study their behaviour under modifications of the original manifold. One possible way to simplify manifolds is what we will call cut-and-paste through the rest of the paper. If a closed $(2k+1)$![]() -dimensional manifold is split by a codimension-one closed manifold $\Sigma$
-dimensional manifold is split by a codimension-one closed manifold $\Sigma$![]() into a union $X_1\cup _\Sigma X_2$
into a union $X_1\cup _\Sigma X_2$![]() , we can often find a manifold $X_0$
, we can often find a manifold $X_0$![]() with $\partial X_0=-\Sigma$
with $\partial X_0=-\Sigma$![]() such that $X_1\cup _\Sigma X_0$
such that $X_1\cup _\Sigma X_0$![]() and $-X_0\cup _\Sigma X_2$
and $-X_0\cup _\Sigma X_2$![]() are “simpler” than $X_1\cup _\Sigma X_2$
are “simpler” than $X_1\cup _\Sigma X_2$![]() . Schematically, we write this modification as
. Schematically, we write this modification as
It is then useful to compare the rho invariant of $X_1\cup _\Sigma X_2$![]() with the sum of the rho invariants of the two other manifolds. Recall that, when $X_i$
with the sum of the rho invariants of the two other manifolds. Recall that, when $X_i$![]() is any of the three manifolds $X_0$
is any of the three manifolds $X_0$![]() , $X_1$
, $X_1$![]() , or $X_2$
, or $X_2$![]() , the subspace
, the subspace
is Lagrangian in $H_{k}(\Sigma ;\mathbb {C}^{n}_\alpha )$![]() with respect to the symplectic form given essentially by the twisted intersection form (we will omit $\alpha$
with respect to the symplectic form given essentially by the twisted intersection form (we will omit $\alpha$![]() from the notation when we are considering the trivial one-dimensional representation). In particular, we can compute their Maslov triple index $\tau (V^{\alpha }_{X_0},\,V_{X_1}^{\alpha },\,V^{\alpha }_{X_2})$
from the notation when we are considering the trivial one-dimensional representation). In particular, we can compute their Maslov triple index $\tau (V^{\alpha }_{X_0},\,V_{X_1}^{\alpha },\,V^{\alpha }_{X_2})$![]() , which is an integer-valued function defined on triples of Lagrangian subspaces (see Definition 3.1). We prove the following cut-and-paste formula for the Atiyah–Patodi–Singer rho invariant.
, which is an integer-valued function defined on triples of Lagrangian subspaces (see Definition 3.1). We prove the following cut-and-paste formula for the Atiyah–Patodi–Singer rho invariant.
Theorem 3.9 Let $X_1,$![]() $X_2$
$X_2$![]() and $X_0$
and $X_0$![]() be compact, oriented manifolds of dimension $2k+1$
be compact, oriented manifolds of dimension $2k+1$![]() with $\partial X_1=-\partial X_0=-\partial X_2=:\Sigma,$
with $\partial X_1=-\partial X_0=-\partial X_2=:\Sigma,$![]() and let $\alpha \colon \pi _1(X_1\cup _\partial X_2)\to U(n)$
and let $\alpha \colon \pi _1(X_1\cup _\partial X_2)\to U(n)$![]() be a representation that extends to $\pi _1(X_0)$
be a representation that extends to $\pi _1(X_0)$![]() . Then, for every choice of such an extension, we have
. Then, for every choice of such an extension, we have
where
with the first Maslov triple index performed on $H_{k}(\partial X_1;\mathbb {C}^{n}_\alpha )$![]() , and the second on $H_{k}(\partial X_1;\mathbb {C})$
, and the second on $H_{k}(\partial X_1;\mathbb {C})$![]() .
.
An analogous cut-and-paste formula for the untwisted eta invariant was proved by Bunke [Reference Bunke5, 2.5]. Formulas related to Theorem 3.9 were also discussed by Kirk and Lesch in connection with their gluing formulas for eta invariants for manifolds with boundary [Reference Kirk and Lesch21, Section 8.3]. In fact, our cut-and-paste formula can also be proved using their results (see [Reference Toffoli28, Section 2.3.4]). Here, however, we give a simple proof which does not involve rho invariants with manifolds with boundary, and it is based on Wall's non-additivity for the signature instead.
The second part of the paper is made up of applications of Theorem 3.9 in the context of link theory, which help relate multivariable signatures to rho invariants. We consider from now on only rho invariants of three-manifolds with one-dimensional representations of the fundamental group. As such representations factor through the first homology in a unique way, we can simply see them as representations of the first homology group. We recall that a $k$![]() -component link $L=K_1\cup \cdots \cup K_k$
-component link $L=K_1\cup \cdots \cup K_k$![]() is said to be $n$
is said to be $n$![]() -coloured if it is considered together with a surjective map $c\colon \{1,\, \dotsc,\, k\}\to \{1,\, \dotsc,\, n\}$
-coloured if it is considered together with a surjective map $c\colon \{1,\, \dotsc,\, k\}\to \{1,\, \dotsc,\, n\}$![]() , which partitions it naturally into $n$
, which partitions it naturally into $n$![]() sublinks $L_1,\, \dotsc,\, L_n$
sublinks $L_1,\, \dotsc,\, L_n$![]() . A component $K_i$
. A component $K_i$![]() is then said to have colour $c(i)$
is then said to have colour $c(i)$![]() . Given an $n$
. Given an $n$![]() -coloured link $L$
-coloured link $L$![]() in $S^{3}$
in $S^{3}$![]() , the Cimasoni–Florens signature is a function
, the Cimasoni–Florens signature is a function
where $\mathbb {T}_*^{n}:=(S^{1}\setminus \{1\})^{n}$![]() . If $n=1$
. If $n=1$![]() , $\sigma _L$
, $\sigma _L$![]() coincides with the Levine–Tristram signature function. Now, let $X_L$
coincides with the Levine–Tristram signature function. Now, let $X_L$![]() be the exterior of $L$
be the exterior of $L$![]() , i.e. the complement of an open tubular neighbourhood of $L$
, i.e. the complement of an open tubular neighbourhood of $L$![]() in $S^{3}$
in $S^{3}$![]() . Then, $X_L$
. Then, $X_L$![]() is a compact, oriented three manifolds with boundary, whose first homology group is a free abelian group generated by the meridians of $L$
is a compact, oriented three manifolds with boundary, whose first homology group is a free abelian group generated by the meridians of $L$![]() . Observe that $\mathbb {T}_*^{n}$
. Observe that $\mathbb {T}_*^{n}$![]() has a natural bijection with the set of representation $H_1(X_L;\mathbb {Z}^{n})\to U(1)$
has a natural bijection with the set of representation $H_1(X_L;\mathbb {Z}^{n})\to U(1)$![]() that send the meridians of components of the same colour $s$
that send the meridians of components of the same colour $s$![]() to a same value $\omega _s\in S^{1}\setminus \{1\}$
to a same value $\omega _s\in S^{1}\setminus \{1\}$![]() (we call these coloured representations): given an element $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}_*^{n}$
(we call these coloured representations): given an element $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}_*^{n}$![]() , we have an associated coloured representation $\alpha$
, we have an associated coloured representation $\alpha$![]() defined by sending the meridian of a component $K_i$
defined by sending the meridian of a component $K_i$![]() to to $\omega _{c(i)}$
to to $\omega _{c(i)}$![]() . The following result, which can be seen as a generalization of (1.2), expresses the multivariable signature of $L$
. The following result, which can be seen as a generalization of (1.2), expresses the multivariable signature of $L$![]() as the rho invariant of a suitable closed three-manifold $Y_L$
as the rho invariant of a suitable closed three-manifold $Y_L$![]() which only depends on $L$
which only depends on $L$![]() . This manifold $Y_L$
. This manifold $Y_L$![]() is built by gluing the link exterior $X_L$
is built by gluing the link exterior $X_L$![]() together with a three-manifold with boundary obtained by plumbing punctured disks in a way that is prescribed by the linking numbers of $L$
together with a three-manifold with boundary obtained by plumbing punctured disks in a way that is prescribed by the linking numbers of $L$![]() . For a precise definition of $Y_L$
. For a precise definition of $Y_L$![]() , see Construction 4.17.
, see Construction 4.17.
Proposition 4.18 Let $L$![]() be an $n$
be an $n$![]() -coloured link. Let $\omega \in \mathbb {T}_*^{n}$
-coloured link. Let $\omega \in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Then, $\alpha$
be the associated coloured representation. Then, $\alpha$![]() can be extended to a representation of $H_1(Y_L;\mathbb {Z})$
can be extended to a representation of $H_1(Y_L;\mathbb {Z})$![]() and, for any choice of an extension, we have
and, for any choice of an extension, we have
The manifold $Y_L$![]() has a very simple description in the case when $L$
has a very simple description in the case when $L$![]() is colour-to-colour algebraically split, i.e. when the total linking number $\operatorname { {lk}}(L_s,\,L_t)$
is colour-to-colour algebraically split, i.e. when the total linking number $\operatorname { {lk}}(L_s,\,L_t)$![]() is $0$
is $0$![]() for every pair of distinct colours $s,\,t$
for every pair of distinct colours $s,\,t$![]() . Under this assumption, we prove two formulas relating the rho invariants of the closed manifolds obtained by the Dehn surgery on $L$
. Under this assumption, we prove two formulas relating the rho invariants of the closed manifolds obtained by the Dehn surgery on $L$![]() with the multivariable signature of $L$
with the multivariable signature of $L$![]() . Given a link $L=K_1\cup \cdots \cup K_k$
. Given a link $L=K_1\cup \cdots \cup K_k$![]() with a rational framing $r=(r_1,\, \dotsc,\, r_k)\in \mathbb {Q}^{k}$
with a rational framing $r=(r_1,\, \dotsc,\, r_k)\in \mathbb {Q}^{k}$![]() , let $\Lambda _r$
, let $\Lambda _r$![]() be the rational matrix with coefficients
be the rational matrix with coefficients

As $\Lambda _r$![]() is a symmetric matrix, we can compute its signature $\operatorname { {sign}} \Lambda _r$
is a symmetric matrix, we can compute its signature $\operatorname { {sign}} \Lambda _r$![]() . Let $S_L(r)$
. Let $S_L(r)$![]() be the closed three-manifold obtained by the Dehn surgery on $L$
be the closed three-manifold obtained by the Dehn surgery on $L$![]() along the rational framing $r$
along the rational framing $r$![]() . We say that a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
. We say that a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() is compatible with $r$
is compatible with $r$![]() , if it extends to $H_1(S_L(r);\mathbb {Z})$
, if it extends to $H_1(S_L(r);\mathbb {Z})$![]() . First, we focus on surgery along integral framings. In this context, a fairly general formula was given by Cimasoni and Florens [Reference Cimasoni and Florens9, Theorem 6.7], extending to the multivariable setting a result of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1] (see also [Reference Gilmer19, Theorem 3.6]). These formulas only consider representations with a finite image and are written in terms of the invariant $\sigma (N,\,\alpha )$
. First, we focus on surgery along integral framings. In this context, a fairly general formula was given by Cimasoni and Florens [Reference Cimasoni and Florens9, Theorem 6.7], extending to the multivariable setting a result of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1] (see also [Reference Gilmer19, Theorem 3.6]). These formulas only consider representations with a finite image and are written in terms of the invariant $\sigma (N,\,\alpha )$![]() of Casson and Gordon (see § 2.3). Rewritten in terms of the rho invariant, the result of Cimasoni and Florens reads as follows.
of Casson and Gordon (see § 2.3). Rewritten in terms of the rho invariant, the result of Cimasoni and Florens reads as follows.
Theorem 4.21 Cimasoni–Florens
Let $L$![]() be a $k$
be a $k$![]() -coloured $k$
-coloured $k$![]() -component link. Let $q\in \mathbb {N}$
-component link. Let $q\in \mathbb {N}$![]() a positive integer and let $n_1,\,\dotsc,\, n_k\in \{1,\,\dotsc,\, p-1\}$
a positive integer and let $n_1,\,\dotsc,\, n_k\in \{1,\,\dotsc,\, p-1\}$![]() be integers, each of which is coprime with $q$
be integers, each of which is coprime with $q$![]() . Let $\omega =(e^{2\pi in _1/q},\, \dotsc,\, e^{2\pi i n_k/q})\in \mathbb {T}_*^{n}$
. Let $\omega =(e^{2\pi in _1/q},\, \dotsc,\, e^{2\pi i n_k/q})\in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Let $g$
be the associated coloured representation. Let $g$![]() be a compatible integral framing on $L$
be a compatible integral framing on $L$![]() . Then, we have
. Then, we have

Theorem 4.21 applies to the signature associated with the maximal colouring, where all distinct link components have different colours, but a formula for any colouring can be easily deduced from it. However, there are some restrictions on the values of $\omega$![]() that limit its use. Under the assumption of $L$
that limit its use. Under the assumption of $L$![]() being colour-to-colour algebraically split, we prove the following formula with no restrictions on the values of $\omega$
being colour-to-colour algebraically split, we prove the following formula with no restrictions on the values of $\omega$![]() .
.
Theorem 4.24 Let $L$![]() be an $n$
be an $n$![]() -coloured link which is colour-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$
-coloured link which is colour-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Let $g$
be the associated coloured representation. Let $g$![]() be a compatible integral framing on $L$
be a compatible integral framing on $L$![]() . Then, we have
. Then, we have

where, for each colour $s$![]() , the values $h_s$
, the values $h_s$![]() and $\theta _s$
and $\theta _s$![]() are determined by
are determined by
Theorem 4.24 is proved by first describing the multivariable signature as a rho invariant using Proposition 4.18, and then applying the cut-and-paste formula (Theorem 3.9) to modify $Y_L$![]() into a disjoint union of $S_L(g)$
into a disjoint union of $S_L(g)$![]() and lens spaces $L(h_s,\,1)$
and lens spaces $L(h_s,\,1)$![]() , for which we can write the rho invariant very explicitly. The proof is completed by a careful computation of the Maslov triple index involved in the cut-and-paste formula.
, for which we can write the rho invariant very explicitly. The proof is completed by a careful computation of the Maslov triple index involved in the cut-and-paste formula.
Suppose now that a stronger assumption on the linking numbers is satisfied, namely that every link component $K_i$![]() has total linking number $0$
has total linking number $0$![]() with all sublinks $L_s$
with all sublinks $L_s$![]() such that $s\ne c(i)$
such that $s\ne c(i)$![]() . We say in this case that $L$
. We say in this case that $L$![]() is component-to-colour algebraically split. Then, as it is easy to verify, there is a particular integer framing $f_L$
is component-to-colour algebraically split. Then, as it is easy to verify, there is a particular integer framing $f_L$![]() (the Seifert framing) which is compatible with all coloured representations $H_1(X_L;\mathbb {Z})\to U(1)$
(the Seifert framing) which is compatible with all coloured representations $H_1(X_L;\mathbb {Z})\to U(1)$![]() . An immediate consequence of Theorem 4.24 is the following.
. An immediate consequence of Theorem 4.24 is the following.
Corollary 4.28 Let $L$![]() be an $n$
be an $n$![]() -coloured link which is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$
-coloured link which is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Then, $\alpha$
be the associated coloured representation. Then, $\alpha$![]() extends to $H_1(S_L(f_L);\mathbb {Z})$
extends to $H_1(S_L(f_L);\mathbb {Z})$![]() and we have
and we have
The analog to Corollary 4.28 for the onecoloured setting was used by Nagel and Powell in studying concordance properties of the Levine–Tristram signature [Reference Nagel and Powell25]. Besides being a useful formula on its own, moreover, Corollary 4.28 is our starting point to prove a result that takes into account (non-integral) rational framings. This is expressed by the next and final result of this paper.
Theorem 4.31 Let $L$![]() be an $n$
be an $n$![]() -coloured, $k$
-coloured, $k$![]() -component link that is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$
-component link that is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon \pi _1(X_L)\to U(1)$
, and let $\alpha \colon \pi _1(X_L)\to U(1)$![]() be the associated coloured representation. Let $r$
be the associated coloured representation. Let $r$![]() be a compatible rational framing on $L$
be a compatible rational framing on $L$![]() . Then, we have
. Then, we have

where $p_i,\,q_i$![]() are coprime integers such that $r_i-f_i=p_i/q_i$
are coprime integers such that $r_i-f_i=p_i/q_i$![]() (here, $f_i$
(here, $f_i$![]() is the $i$
is the $i$![]() -th coefficient of the Seifert framing).
-th coefficient of the Seifert framing).
As in the proof Theorem 4.24, lens spaces arise from the cut-and-paste construction. In this case, we do not spell out the values of their rho invariant in the statement of the theorem, as this would make the formula more cumbersome. Note, however, that these values can always be easily computed (see Proposition 2.10).
Observe that onecoloured links are a special case of component-to-colour algebraically split links. In particular, Theorem 4.31 gives a new formula relating rho invariants with the Levine–Tristram signature.
Remark Whenever not stated otherwise, all manifolds are assumed to be smooth.
Outline of the paper
In §2, we review the basics about twisted signatures and Atiyah–Patodi–Singer rho invariants. We illustrate then a formula for the rho invariant of a three-dimensional lens space. In §3, we review the Maslov triple index of Lagrangian subspaces and Wall's non-additivity theorem for the signature. We prove then our cut-and-paste formula (Theorem 3.9). In §4, we develop the applications in the knot theory. We first prove the basic formula relating rho invariants and multivariable signatures (Proposition 4.18), and then use it to show results about integer (Theorem 4.24) and rational (Theorem 4.31) Dehn surgery.
2. Twisted signatures and rho invariants
In § 2.1, we review the definition of twisted homology and twisted signatures and set notation for these. In § 2.2, we recall the basics about Atiyah–Patodi–Singer eta and rho invariants. In § 2.3, we underline the relation between these invariants and an invariant of Casson and Gordon. In § 2.4, we give a reinterpretation of a well-known computation for the rho invariant of three-dimensional lens spaces.
2.1. Twisted intersection forms and signatures
Let $M$![]() be a connected, compact, oriented manifold of dimension $2k$
be a connected, compact, oriented manifold of dimension $2k$![]() with a representation $\alpha \colon \pi _1(M) \to U(n)$
with a representation $\alpha \colon \pi _1(M) \to U(n)$![]() for some $n\in \mathbb {N}$
for some $n\in \mathbb {N}$![]() . Let $\pi :=\pi _1(M)$
. Let $\pi :=\pi _1(M)$![]() . Let $\widetilde {M}$
. Let $\widetilde {M}$![]() be the universal cover of $M$
be the universal cover of $M$![]() , so that $\pi$
, so that $\pi$![]() acts on the left on $C_*(\widetilde {M})$
acts on the left on $C_*(\widetilde {M})$![]() by deck transformations, and on $\mathbb {C}^{n}$
by deck transformations, and on $\mathbb {C}^{n}$![]() through the representation $\alpha$
through the representation $\alpha$![]() (we write $\mathbb {C}^{n}_\alpha$
(we write $\mathbb {C}^{n}_\alpha$![]() for the left $\mathbb {Z}[\pi ]$
for the left $\mathbb {Z}[\pi ]$![]() -module coming from this action). We consider the twisted homology groups
-module coming from this action). We consider the twisted homology groups

where the $t$![]() denotes the fact that we are turning the left $\mathbb {Z}[\pi ]$
denotes the fact that we are turning the left $\mathbb {Z}[\pi ]$![]() -module structure of $\mathbb {C}^{n}$
-module structure of $\mathbb {C}^{n}$![]() into a right one by means of the involution $g\to g^{-1}$
into a right one by means of the involution $g\to g^{-1}$![]() in $\pi$
in $\pi$![]() . Relative homology and cohomology groups are defined in a similar manner, as well as twisted homology groups with different $\mathbb {Z}[\pi ]$
. Relative homology and cohomology groups are defined in a similar manner, as well as twisted homology groups with different $\mathbb {Z}[\pi ]$![]() -modules (see e.g [Reference Friedl, Nagel, Orson and Powell18, Definition A.2]).
-modules (see e.g [Reference Friedl, Nagel, Orson and Powell18, Definition A.2]).
Remark 2.1 If $M=M_1\sqcup \cdots \sqcup M_N$![]() is a disjoint union of connected manifolds $M_j$
is a disjoint union of connected manifolds $M_j$![]() , we will make the abuse of notation of writing $\alpha \colon \pi _1(M) \to U(n)$
, we will make the abuse of notation of writing $\alpha \colon \pi _1(M) \to U(n)$![]() to denote a collection of representations $\alpha _j\colon \pi _1(M_j)\to U(n)$
to denote a collection of representations $\alpha _j\colon \pi _1(M_j)\to U(n)$![]() . In this case, we define then
. In this case, we define then

We recall the following facts.
Fact 1 Given a subset $N\subseteq M$![]() , there is a well-defined cup product [Reference Friedl, Nagel, Orson and Powell18, Lemma A.11]
, there is a well-defined cup product [Reference Friedl, Nagel, Orson and Powell18, Lemma A.11]
where $\overline {\alpha }$![]() denotes the complex-conjugate representation of $\alpha$
denotes the complex-conjugate representation of $\alpha$![]() .
.
Fact 2 As the representation $\alpha$![]() is Hermitian, the standard Hermitian product of $\mathbb {C}^{n}$
is Hermitian, the standard Hermitian product of $\mathbb {C}^{n}$![]() gives rise to a well-defined map of $\mathbb {Z}[\pi ]$
gives rise to a well-defined map of $\mathbb {Z}[\pi ]$![]() -modules $\mathbb {C}^{n}_\alpha \otimes _\mathbb {Z}\mathbb {C}^{n}_{\overline {\alpha }}\to \mathbb {C}$
-modules $\mathbb {C}^{n}_\alpha \otimes _\mathbb {Z}\mathbb {C}^{n}_{\overline {\alpha }}\to \mathbb {C}$![]() (where $\mathbb {C}$
(where $\mathbb {C}$![]() is the $\mathbb {Z}[\pi ]$
is the $\mathbb {Z}[\pi ]$![]() -module associated with the trivial one-dimensional representation). This induces a group homomorphism
-module associated with the trivial one-dimensional representation). This induces a group homomorphism
Composing the above map with the cup product of Fact 1, and observing that $H^{q}(M,\,N;\mathbb {C}^{n}_{\overline {\alpha }})$![]() coincides with the complex-conjugate vector space $\overline {H^{q}(M,\,N;\mathbb {C}^{n}_\alpha )}$
coincides with the complex-conjugate vector space $\overline {H^{q}(M,\,N;\mathbb {C}^{n}_\alpha )}$![]() , we get a bilinear map
, we get a bilinear map
Fact 3 There are twisted Poincaré duality isomorphisms [Reference Friedl, Nagel, Orson and Powell18, Theorem A.15]
Fact 4 Since the representation $\alpha$![]() is unitary, the evaluation map in twisted homology gives rise to an isomorphism [Reference Conway and Nagel11, Lemma 2.7]
is unitary, the evaluation map in twisted homology gives rise to an isomorphism [Reference Conway and Nagel11, Lemma 2.7]
Using the first three facts, we define the twisted intersection form as the sesquilinear form
given by
(compare e.g. with [Reference Friedl, Nagel, Orson and Powell18, Section 13]). As for the ordinary intersection pairing, the properties of the cup product make the form $I_M^{\alpha }$![]() Hermitian if $k$
Hermitian if $k$![]() is even and skew-Hermitian if $k$
is even and skew-Hermitian if $k$![]() is odd. This leads to the following definition.
is odd. This leads to the following definition.
Definition 2.2 Let $M$![]() be a compact oriented manifold of dimension $2k$
be a compact oriented manifold of dimension $2k$![]() with a representation $\alpha \colon \pi _1(M)\to U(n)$
with a representation $\alpha \colon \pi _1(M)\to U(n)$![]() . The signature of $M$
. The signature of $M$![]() twisted by $\alpha$
twisted by $\alpha$![]() is the integer
is the integer

where $\operatorname { {sign}}$![]() denotes the signature of a Hermitian form.
denotes the signature of a Hermitian form.
Observe that the form $I^{\alpha }_M$![]() can be defined alternatively using the sequence of maps
can be defined alternatively using the sequence of maps
(see e.g. [Reference Conway, Nagel and Toffoli12, Definition 2.7]), where $\operatorname { {ev}}_\mathbb {C}$![]() is the map discussed in Fact 4. From this point of view, we see that the radical of $I_M^{\alpha }$
is the map discussed in Fact 4. From this point of view, we see that the radical of $I_M^{\alpha }$![]() coincides with the kernel of $j_*$
coincides with the kernel of $j_*$![]() , as the two other maps in the composition are isomorphisms. As a consequence, $I_M^{\alpha }$
, as the two other maps in the composition are isomorphisms. As a consequence, $I_M^{\alpha }$![]() is non-degenerate whenever $M$
is non-degenerate whenever $M$![]() is closed.
is closed.
2.2. Basics on the rho invariant
Let $N$![]() be a closed, oriented, Riemannian manifold of dimension $2k+1$
be a closed, oriented, Riemannian manifold of dimension $2k+1$![]() , with a representation $\alpha \colon \pi _1(N)\to U(n)$
, with a representation $\alpha \colon \pi _1(N)\to U(n)$![]() . Let $E_\alpha \to N$
. Let $E_\alpha \to N$![]() be the associated flat vector bundle, and consider the subspace
be the associated flat vector bundle, and consider the subspace

of twisted differential forms of even degree (see [Reference Atiyah, Patodi and Singer2, Section 2] for details). Let $D^{\alpha }_N$![]() be the twisted odd signature operator, i.e. the first-order differential operator on $\Omega ^{\operatorname { {ev}}}(N,\, E_\alpha )$
be the twisted odd signature operator, i.e. the first-order differential operator on $\Omega ^{\operatorname { {ev}}}(N,\, E_\alpha )$![]() defined by
defined by
The operator $D^{\alpha }_N$![]() can be extended to a self-adjoint elliptic operator with discrete spectrum and, by the results of Atiyah, Patodi, and Singer [Reference Atiyah, Patodi and Singer3, Theorem 4.5], its eta function
can be extended to a self-adjoint elliptic operator with discrete spectrum and, by the results of Atiyah, Patodi, and Singer [Reference Atiyah, Patodi and Singer3, Theorem 4.5], its eta function

has a meromorphic extension which is holomorphic at $s=0$![]() , leading to the eta invariant
, leading to the eta invariant
We say that a compact Riemannian manifold $M$![]() has metric of product form near the boundary, if there exists a neighbourhood of $\partial M$
has metric of product form near the boundary, if there exists a neighbourhood of $\partial M$![]() that is isometric to $(-\varepsilon,\, 0] \times \partial M$
that is isometric to $(-\varepsilon,\, 0] \times \partial M$![]() with the product metric. The main result about the eta invariant of the twisted signature operator is the following [Reference Atiyah, Patodi and Singer2, Theorem 2.2].
with the product metric. The main result about the eta invariant of the twisted signature operator is the following [Reference Atiyah, Patodi and Singer2, Theorem 2.2].
Theorem 2.3 Atiyah–Patodi–Singer
Let $M$![]() be an even-dimensional compact, oriented manifold with $\partial M=N$
be an even-dimensional compact, oriented manifold with $\partial M=N$![]() , equipped with Riemannian metric of product form near $N$
, equipped with Riemannian metric of product form near $N$![]() , and let $\alpha \colon \pi _1(M)\to U(n)$
, and let $\alpha \colon \pi _1(M)\to U(n)$![]() be a representation. Then
be a representation. Then
where $L(p)$![]() is the Hirzebruch $L$
is the Hirzebruch $L$![]() -polynomial in the Pontryagin forms of $M$
-polynomial in the Pontryagin forms of $M$![]() .
.
Note that both summands on the right-hand term depend on the Riemannian metric on $N$![]() . We shall not dwell upon the geometrical significance of the integral of the $L$
. We shall not dwell upon the geometrical significance of the integral of the $L$![]() -polynomial, as it is going to get simplified soon.
-polynomial, as it is going to get simplified soon.
Remark 2.4 The restriction of $\alpha \colon \pi _1(M) \to U(n)$![]() to a representation of $\pi _1(N)$
to a representation of $\pi _1(N)$![]() is made by composing $\alpha$
is made by composing $\alpha$![]() with the natural map $\pi _1(N)\to \pi _1(M)$
with the natural map $\pi _1(N)\to \pi _1(M)$![]() . If $N$
. If $N$![]() is not connected, a map $\pi _1(N_1)\to \pi _1(M)$
is not connected, a map $\pi _1(N_1)\to \pi _1(M)$![]() for each connected component $N_i$
for each connected component $N_i$![]() of $N$
of $N$![]() can be obtained by choosing appropriate paths between base points. The restriction $\alpha \colon \pi _1(N)\to U(n)$
can be obtained by choosing appropriate paths between base points. The restriction $\alpha \colon \pi _1(N)\to U(n)$![]() must be interpreted as the collection of the representations $\pi _1(N_i)\to U(n)$
must be interpreted as the collection of the representations $\pi _1(N_i)\to U(n)$![]() for all connected components $N_i$
for all connected components $N_i$![]() . The invariant $\eta _\alpha (N)$
. The invariant $\eta _\alpha (N)$![]() is defined in this case as the sum of the eta invariants of the $N_i$
is defined in this case as the sum of the eta invariants of the $N_i$![]() 's.
's.
For the eta invariant associated with the untwisted odd signature operator $D_N$![]() on $\Omega ^{\operatorname { {ev}}}(N,\, \mathbb {C})$
on $\Omega ^{\operatorname { {ev}}}(N,\, \mathbb {C})$![]() , we use the notation $\eta (N):=\eta (D_N)$
, we use the notation $\eta (N):=\eta (D_N)$![]() . Following Atiyah, Patodi, and Singer [Reference Atiyah, Patodi and Singer2], we are now going to define the rho invariant.
. Following Atiyah, Patodi, and Singer [Reference Atiyah, Patodi and Singer2], we are now going to define the rho invariant.
Definition 2.5 Let $N$![]() be a closed, oriented manifold of odd dimension, and let $\alpha \colon \pi _1(N)\to U(n)$
be a closed, oriented manifold of odd dimension, and let $\alpha \colon \pi _1(N)\to U(n)$![]() be a representation. The Atiyah–Patodi–Singer rho invariant of $N$
be a representation. The Atiyah–Patodi–Singer rho invariant of $N$![]() associated with $\alpha$
associated with $\alpha$![]() is the real number
is the real number
where the eta invariants are computed for an arbitrary Riemannian metric on $N$![]() .
.
We shall see in a moment that the difference $\eta _\alpha (N)-n\,\eta (N)$![]() is independent of the Riemannian metric, so that $\rho _\alpha (N)$
is independent of the Riemannian metric, so that $\rho _\alpha (N)$![]() is well defined. Moreover, $\rho _\tau (N)$
is well defined. Moreover, $\rho _\tau (N)$![]() is $0$
is $0$![]() for trivial representations $\tau$
for trivial representations $\tau$![]() , and it satisfies
, and it satisfies
The main theorem about the rho invariant is the following.
Theorem 2.6 Atiyah–Patodi–Singer
(i) $\rho _\alpha (N)$
 is independent of the Riemannian metric on $N$
is independent of the Riemannian metric on $N$ .
.(ii) If $M$
 is a compact, oriented manifold with $\partial M=N$
is a compact, oriented manifold with $\partial M=N$ and $\alpha$
and $\alpha$ extends to $M,$
extends to $M,$ then
\[ \rho_\alpha(N)= n\,\sigma(M)-\sigma_\alpha(M). \]
then
\[ \rho_\alpha(N)= n\,\sigma(M)-\sigma_\alpha(M). \]
Proof. Both statements are easy consequences of Theorem 2.3. See [Reference Atiyah, Patodi and Singer2, Theorem 2.4].
We state one more well-known result that will turn useful later on.
Proposition 2.7 Let $\Sigma$![]() be a closed, oriented surface, and let $\psi \colon \pi _1(\Sigma \times S^{1})\to U(1)$
be a closed, oriented surface, and let $\psi \colon \pi _1(\Sigma \times S^{1})\to U(1)$![]() be a representation. Then $\rho _\psi (\Sigma \times S^{1})=0.$
be a representation. Then $\rho _\psi (\Sigma \times S^{1})=0.$![]()
Proof. See e.g. [Reference Conway, Nagel and Toffoli12, Lemma 4.2].
2.3. Rho invariants and Casson–Gordon invariants
We will now review the definition of an invariant of Casson and Gordon and relate it to the Atiyah–Patodi–Singer rho invariant. Let $N$![]() be a closed, oriented three manifolds, and let $\alpha \colon H_1(N;\mathbb {Z})\to U(1)$
be a closed, oriented three manifolds, and let $\alpha \colon H_1(N;\mathbb {Z})\to U(1)$![]() be a representation. Assume that the image of $\alpha$
be a representation. Assume that the image of $\alpha$![]() is finite. Using a bordism argument, Casson and Gordon observe that there exists a compact, oriented four-manifold $W$
is finite. Using a bordism argument, Casson and Gordon observe that there exists a compact, oriented four-manifold $W$![]() such that the boundary of $W$
such that the boundary of $W$![]() is the disjoint union of $r$
is the disjoint union of $r$![]() copies of $N$
copies of $N$![]() for some $r\in \mathbb {N}$
for some $r\in \mathbb {N}$![]() (we will write $\partial W =r N$
(we will write $\partial W =r N$![]() ) with a representation $\alpha '\colon H_1(W;\mathbb {Z})\to U(1)$
) with a representation $\alpha '\colon H_1(W;\mathbb {Z})\to U(1)$![]() that restrict to $\alpha$
that restrict to $\alpha$![]() on each boundary component [Reference Casson and Gordon8, p. 183]. They define then an invariant as
on each boundary component [Reference Casson and Gordon8, p. 183]. They define then an invariant as
By additivity of the signature and again some bordism theory, they show that the invariant $\sigma (N,\,\alpha )$![]() is independent of the choice of $W$
is independent of the choice of $W$![]() and of the extension $\alpha '$
and of the extension $\alpha '$![]() [Reference Casson and Gordon8, p. 183–184] (see also [Reference Conway, Nagel and Toffoli12, Corollary 2.11] for a more detailed version of their proof). Using the Atiyah–Patodi–Singer index theorem, their invariant can be immediately reinterpreted as an Atiyah–Patodi–Singer rho invariant. We state this explicitly for further reference, albeit it is surely known to the experts.
[Reference Casson and Gordon8, p. 183–184] (see also [Reference Conway, Nagel and Toffoli12, Corollary 2.11] for a more detailed version of their proof). Using the Atiyah–Patodi–Singer index theorem, their invariant can be immediately reinterpreted as an Atiyah–Patodi–Singer rho invariant. We state this explicitly for further reference, albeit it is surely known to the experts.
Proposition 2.8 Let $N$![]() be a closed, oriented three-manifold, and let $\alpha \colon H_1(N;\mathbb {Z})\to U(1)$
be a closed, oriented three-manifold, and let $\alpha \colon H_1(N;\mathbb {Z})\to U(1)$![]() be a representation with finite image. Then, we have
be a representation with finite image. Then, we have
Proof. Let $W$![]() be a compact, oriented four-manifold with $\partial W = rN$
be a compact, oriented four-manifold with $\partial W = rN$![]() , with a representation $\alpha '\colon H_1(W;\mathbb {Z})\to U(1)$
, with a representation $\alpha '\colon H_1(W;\mathbb {Z})\to U(1)$![]() that restricts to $\alpha$
that restricts to $\alpha$![]() as discussed above, so that $\sigma (N,\,\alpha )$
as discussed above, so that $\sigma (N,\,\alpha )$![]() is described by (2.2). Using Theorem 2.6, on the other hand, we have
is described by (2.2). Using Theorem 2.6, on the other hand, we have
Comparing this with (2.2), we obtain the desired statement.
2.4. The rho invariant of lens spaces
Given coprime integers $p$![]() and $q$
and $q$![]() , the three-dimensional lens space $L(p,\,q)$
, the three-dimensional lens space $L(p,\,q)$![]() can be built as the union of two solid tori $Y_1,\,Y_2$
can be built as the union of two solid tori $Y_1,\,Y_2$![]() along any orientation-reversing diffeomorphism $f\colon \partial Y_2\to \partial Y_1$
along any orientation-reversing diffeomorphism $f\colon \partial Y_2\to \partial Y_1$![]() such that
such that
where $\mu _1,\, \mu _2$![]() are the meridians, respectively, of $Y_1,\, Y_2$
are the meridians, respectively, of $Y_1,\, Y_2$![]() , and $\lambda _1$
, and $\lambda _1$![]() is a longitude of $Y_1$
is a longitude of $Y_1$![]() . This construction is well defined for both positive and negative values of $p$
. This construction is well defined for both positive and negative values of $p$![]() and $q$
and $q$![]() . For positive $p$
. For positive $p$![]() it coincides, up to some explicit orientation-preserving diffeomorphism, with the classical definition of $L(p,\,q)$
it coincides, up to some explicit orientation-preserving diffeomorphism, with the classical definition of $L(p,\,q)$![]() as a quotient of $S^{3}$
as a quotient of $S^{3}$![]() (compare with [Reference Friedl15, Lemma 91.3]). In general, there are orientation-preserving diffeomorphisms
(compare with [Reference Friedl15, Lemma 91.3]). In general, there are orientation-preserving diffeomorphisms
In particular, for both positive and negative $p$![]() , we have an identification of $\pi _1(L(p,\,q))$
, we have an identification of $\pi _1(L(p,\,q))$![]() with $\mathbb {Z}/p$
with $\mathbb {Z}/p$![]() , and under this identification, the element $[1]\in \mathbb {Z}/p$
, and under this identification, the element $[1]\in \mathbb {Z}/p$![]() corresponds to the generator of $\pi _1(Y_1)$
corresponds to the generator of $\pi _1(Y_1)$![]() .
.
Rho invariants of three-dimensional lens spaces can be computed explicitly. As every representation $\alpha \colon \mathbb {Z}/p\to U(n)$![]() can be written as a direct sum of one-dimensional representations, we shall focus on one-dimensional representations. Moreover, we shall exclude the case $p=0$
can be written as a direct sum of one-dimensional representations, we shall focus on one-dimensional representations. Moreover, we shall exclude the case $p=0$![]() , as $L(0,\,1)$
, as $L(0,\,1)$![]() is diffeomorphic to $S^{2}\times S^{1}$
is diffeomorphic to $S^{2}\times S^{1}$![]() and its rho invariant is $0$
and its rho invariant is $0$![]() for any choice of $\alpha$
for any choice of $\alpha$![]() . We observe in this case that the representations $\alpha \colon \mathbb {Z}/p\to U(1)$
. We observe in this case that the representations $\alpha \colon \mathbb {Z}/p\to U(1)$![]() are in a natural bijection with the set of $\left |{p}\right |$
are in a natural bijection with the set of $\left |{p}\right |$![]() th roots of unity: to each such root $\omega$
th roots of unity: to each such root $\omega$![]() , we associate the representation $\alpha _\omega$
, we associate the representation $\alpha _\omega$![]() sending $1$
sending $1$![]() to $\omega$
to $\omega$![]() .
.
Notation 2.9 Given a $\left |{p}\right |$![]() th root of unity $\omega$
th root of unity $\omega$![]() , we write
, we write
Formulas for the rho invariants of lens spaces were given since the original paper of Atiyah, Patodi and Singer [Reference Atiyah, Patodi and Singer2, Proposition 2.12]. Introducing the periodic sawtooth function $\left ( \! \left ({\cdot }\right ) \! \right )\colon \mathbb {R}\to (-\frac {1}{2},\, \frac {1}{2})$![]() defined by
defined by

we give the following description.
Proposition 2.10 Let $p,\,q$![]() be two coprime integers with $p\ne 0,$
be two coprime integers with $p\ne 0,$![]() and let $\zeta =e^{2\pi i /p}$
and let $\zeta =e^{2\pi i /p}$![]() . Then, for $k\in \{0,\,1,\,\dotsc,\, \left |{p}\right |-1\},$
. Then, for $k\in \{0,\,1,\,\dotsc,\, \left |{p}\right |-1\},$![]() we have
we have

Proof. We first suppose $p,\,q>0$![]() . Set $z:=e^{2\pi i n/p}$
. Set $z:=e^{2\pi i n/p}$![]() , with $n=\gcd (p,\,k)$
, with $n=\gcd (p,\,k)$![]() , and set $r:=k/n$
, and set $r:=k/n$![]() . Then, we have $\zeta ^{kq}=z^{rq}$
. Then, we have $\zeta ^{kq}=z^{rq}$![]() . The representation sending $1$
. The representation sending $1$![]() to $\omega ^{q}$
to $\omega ^{q}$![]() has as its image the set of $m$
has as its image the set of $m$![]() th roots of unity, with $m$
th roots of unity, with $m$![]() such that $p=mn$
such that $p=mn$![]() . In this setting, Casson and Gordon [Reference Casson and Gordon8, pp.187–188] proved that
. In this setting, Casson and Gordon [Reference Casson and Gordon8, pp.187–188] proved that
where $\Delta (x,\,y)$![]() is the triangle with vertices $(0,\,0)$
is the triangle with vertices $(0,\,0)$![]() , $(x,\,0)$
, $(x,\,0)$![]() and $(x,\,y)$
and $(x,\,y)$![]() and the number $\operatorname { {int}}(\Delta (x,\,y))$
and the number $\operatorname { {int}}(\Delta (x,\,y))$![]() is given by counting:
is given by counting:
• $+1$
 for every point of $\mathbb {Z}^{2}$
for every point of $\mathbb {Z}^{2}$ that lies in the interior of $\Delta (x,\,y)$
that lies in the interior of $\Delta (x,\,y)$ ;
;• $+1/2$
 for every point of $\mathbb {Z}^{2}$
for every point of $\mathbb {Z}^{2}$ that lies in the interior of its edges;
that lies in the interior of its edges;• $+1/4$
 for every point of $\mathbb {Z}^{2}\setminus \{(0,\,0)\}$
for every point of $\mathbb {Z}^{2}\setminus \{(0,\,0)\}$ that coincides with one of the vertices.
that coincides with one of the vertices.
Using Proposition 2.8 and the definition of $r$![]() , we rewrite (2.3) as
, we rewrite (2.3) as
We will now express the right-hand term of (2.4) in a more explicit way. First of all, it is clear that $4\operatorname { {area}}\Delta (k,\,{\displaystyle \frac {kq}{p}})= {\displaystyle \frac {2q}{p}}k^{2}.$![]() Moreover, we can count the lattice points inside the triangle by following vertical lines $\{(x,\,y)\,\vert \,x=j\}$
Moreover, we can count the lattice points inside the triangle by following vertical lines $\{(x,\,y)\,\vert \,x=j\}$![]() , for $j=1,\,\ldots,\,k$
, for $j=1,\,\ldots,\,k$![]() , and then summing over $j$
, and then summing over $j$![]() . We obtain
. We obtain

Taking the difference, we obtain thus

Expanding the expression in the statement, it is now immediate to see that it coincides with (2.5). As the sawtooth function $\left ( \! \left ({\cdot }\right ) \! \right )$![]() is odd, we see that both sides of the identity change sign when either $p$
is odd, we see that both sides of the identity change sign when either $p$![]() or $q$
or $q$![]() is changed of sign. As a consequence, the result keeps holding for non-positive choices of $p$
is changed of sign. As a consequence, the result keeps holding for non-positive choices of $p$![]() and $q$
and $q$![]() .
.
Corollary 2.11 Let $n$![]() be any integer, and let $\omega \in U(1)$
be any integer, and let $\omega \in U(1)$![]() be an $\left |{n}\right |$
be an $\left |{n}\right |$![]() th root of unity. Then, we have
th root of unity. Then, we have
where $\theta \in [0,\,1)$![]() is such that $\omega =e^{2\pi i\theta }$
is such that $\omega =e^{2\pi i\theta }$![]() .
.
Proof. For $n=0$![]() , we have $\rho (L(n,\,1),\,\omega )=0$
, we have $\rho (L(n,\,1),\,\omega )=0$![]() for all $\omega \in U(1)$
for all $\omega \in U(1)$![]() because $L(0,\,1)=S^{2}\times S^{1}$
because $L(0,\,1)=S^{2}\times S^{1}$![]() , so that the result is trivially satisfied in this case. For $n>0$
, so that the result is trivially satisfied in this case. For $n>0$![]() , there has to be a $k\in \{0,\,1,\, \cdots n-1\}$
, there has to be a $k\in \{0,\,1,\, \cdots n-1\}$![]() such that $\theta =k/n$
such that $\theta =k/n$![]() , with $k\in \{0,\,1,\, \cdots n-1\}$
, with $k\in \{0,\,1,\, \cdots n-1\}$![]() . From (2.5), we easily see that
. From (2.5), we easily see that
and the desired formula is satisfied in this case. For negative $n$![]() , we obtain now from the last equation that
, we obtain now from the last equation that
which leads to the general formula of the statement.
Remark 2.12 Proposition 2.10 can be used to write rho invariants of lens spaces as a difference of Dedekind–Rademacher sums. See [Reference Toffoli28, Theorem 3.3.27].
3. The cut-and-paste formula
In § 3.1, we recall the definition of the Maslov triple index of three Lagrangian subspaces in a complex symplectic space. In § 3.3, we review a (non-)additivity theorem of Wall for signatures of manifolds under some fairly general notion of gluing. In Section 3.4, we prove the cut-and-paste formula for the Atiyah–Patodi–Singer rho invariants (Theorem 3.9), which is the main result of this section.
3.1. Complex symplectic spaces and the Maslov triple index
A complex symplectic space is a pair $(H,\,\omega )$![]() such that $H$
such that $H$![]() is a finite-dimensional complex vector space, and $\omega \colon H\times H\to \mathbb {C}$
is a finite-dimensional complex vector space, and $\omega \colon H\times H\to \mathbb {C}$![]() is a non-degenerate skew-Hermitian form, called the symplectic form. We shall often omit $\omega$
is a non-degenerate skew-Hermitian form, called the symplectic form. We shall often omit $\omega$![]() from the notation and simply call $H$
from the notation and simply call $H$![]() a complex symplectic space. We recall that a subspace $L\subseteq H$
a complex symplectic space. We recall that a subspace $L\subseteq H$![]() is Lagrangian if it coincides with its orthogonal complement with respect to the symplectic form $\omega$
is Lagrangian if it coincides with its orthogonal complement with respect to the symplectic form $\omega$![]() . Let $\mathcal {L} ag(H)$
. Let $\mathcal {L} ag(H)$![]() denote the set of all Lagrangian subspaces of $H$
denote the set of all Lagrangian subspaces of $H$![]() . We are now going to define a function
. We are now going to define a function
Given three Lagrangian subspaces $L_1,\, L_2,\, L_3\in \mathcal {L} ag(H)$![]() , it is immediate to verify that the sesquilinear form
, it is immediate to verify that the sesquilinear form
(with $a_1,\,b_1\in L_1$![]() and $a_2,\,b_2\in L_2$
and $a_2,\,b_2\in L_2$![]() ) is well defined and Hermitian. In particular, we can give the following definition.
) is well defined and Hermitian. In particular, we can give the following definition.
Definition 3.1 The Maslov triple index of $(L_1,\,L_2,\,L_3)$![]() is the integer
is the integer
The Maslov triple index satisfies several elementary properties, among which are the following two.
Proposition 3.2
(i) Let $L_1,\,L_2,\,L_3\in \mathcal {L} ag (H),$
 and let $\alpha$
and let $\alpha$ be a permutation of the set $\{1,\,2,\,3\}$
be a permutation of the set $\{1,\,2,\,3\}$ . Then
\[ \tau(L_{\alpha(1)}, L_{\alpha(2)}, L_{\alpha(3)})= {\operatorname{sgn}}(\alpha)\,\tau(L_1, L_2, L_3). \]In particular, the Maslov triple index vanishes whenever two of the Lagrangians coincide.
. Then
\[ \tau(L_{\alpha(1)}, L_{\alpha(2)}, L_{\alpha(3)})= {\operatorname{sgn}}(\alpha)\,\tau(L_1, L_2, L_3). \]In particular, the Maslov triple index vanishes whenever two of the Lagrangians coincide.
(ii) Let $L_1,\,L_2,\,L_3,\, L_4\in \mathcal {L} ag (H)$
 . Then, $\tau$
. Then, $\tau$ satisfies the cocycle equation
\[ \tau(L_1, L_2, L_3) -\tau(L_1, L_2, L_4)+ \tau(L_1, L_3, L_4)-\tau(L_2, L_3, L_4) =0. \]
satisfies the cocycle equation
\[ \tau(L_1, L_2, L_3) -\tau(L_1, L_2, L_4)+ \tau(L_1, L_3, L_4)-\tau(L_2, L_3, L_4) =0. \]
Proof. See e.g. [Reference Cappell, Lee and Miller6, Section 8] for proofs in the real symplectic setting. These can be transferred verbatim to the complex symplectic one.
Example 3.3 Suppose that $(H,\,\omega )$![]() is a complex symplectic space of dimension $2$
is a complex symplectic space of dimension $2$![]() . Let $(\mu,\,\lambda )$
. Let $(\mu,\,\lambda )$![]() be an ordered basis in which $\omega$
be an ordered basis in which $\omega$![]() is represented by the matrix $\left (\begin {smallmatrix} 0 & -1\\1 & 0\end {smallmatrix}\right )$
is represented by the matrix $\left (\begin {smallmatrix} 0 & -1\\1 & 0\end {smallmatrix}\right )$![]() , i.e. such that
, i.e. such that
we shall call such pair a symplectic basis. Then, it is easy to verify that a one-dimensional subspace is Lagrangian if and only if it is the span of some vector $a\mu +b\lambda$![]() with $a,\,b\in \mathbb {R}$
with $a,\,b\in \mathbb {R}$![]() . We set in this case the notation
. We set in this case the notation
Using the definition of the Maslov triple index, we easily compute that
3.2. Complex symplectic spaces and twisted homology
In the applications, complex symplectic spaces will arise from the following setting. Let $\Sigma$![]() be a $2k$
be a $2k$![]() -dimensional closed, oriented manifold, and let $\alpha \colon \pi _1(\Sigma )\to U(n)$
-dimensional closed, oriented manifold, and let $\alpha \colon \pi _1(\Sigma )\to U(n)$![]() be a representation. As we have seen, the twisted intersection form on $H:=H_{k}(\Sigma ;\mathbb {C}^{n}_\alpha )$
be a representation. As we have seen, the twisted intersection form on $H:=H_{k}(\Sigma ;\mathbb {C}^{n}_\alpha )$![]() is Hermitian if $k$
is Hermitian if $k$![]() is even, and it is skew-Hermitian if $k$
is even, and it is skew-Hermitian if $k$![]() is odd. Moreover, it is non-degenerate because $\Sigma$
is odd. Moreover, it is non-degenerate because $\Sigma$![]() is closed. We can thus always consider the non-degenerate, skew-Hermitian form
is closed. We can thus always consider the non-degenerate, skew-Hermitian form

which makes the pair $(H,\,\omega )$![]() a complex symplectic space. We introduce the following notation.
a complex symplectic space. We introduce the following notation.
Notation 3.4 Given a compact, connected $(2k+1)$![]() -dimensional manifold $X$
-dimensional manifold $X$![]() with a representation $\alpha \colon \pi _1(X)\to U(n)$
with a representation $\alpha \colon \pi _1(X)\to U(n)$![]() , we set
, we set
A well-known argument based on Poincaré duality shows that $V_X^{\alpha }$![]() is a Lagrangian subspace of $H_k(\partial X;\mathbb {C}^{n}_\alpha )$
is a Lagrangian subspace of $H_k(\partial X;\mathbb {C}^{n}_\alpha )$![]() with respect to $\omega$
with respect to $\omega$![]() (compare with [Reference Degtyarev, Florens and Lecuona14, Lemma 2.14] and [Reference Toffoli28, Proposition 1.4.6]). We can thus give the following definition.
(compare with [Reference Degtyarev, Florens and Lecuona14, Lemma 2.14] and [Reference Toffoli28, Proposition 1.4.6]). We can thus give the following definition.
Definition 3.5 Let $X$![]() be compact, connected manifold of dimension $2k+1$
be compact, connected manifold of dimension $2k+1$![]() , and let $\alpha \colon \pi _1(X)\to U(n)$
, and let $\alpha \colon \pi _1(X)\to U(n)$![]() be a representation. We refer to $V_X^{\alpha }$
be a representation. We refer to $V_X^{\alpha }$![]() as the canonical Lagrangian associated with $X$
as the canonical Lagrangian associated with $X$![]() and $\alpha$
and $\alpha$![]() .
.
3.3. Wall's non-additivity of the signature
We shall now review a result of Wall. We start with some notation that will be useful throughout the paper.
Notation 3.6 Given two topological spaces $X,\,Y$![]() with a common subspace $A$
with a common subspace $A$![]() , we set
, we set
where $\sim$![]() is the relation that identifies every element in $A\subseteq X$
is the relation that identifies every element in $A\subseteq X$![]() with its copy in $A\subseteq Y$
with its copy in $A\subseteq Y$![]() . We say that $X\cup _A Y$
. We say that $X\cup _A Y$![]() is obtained by gluing $X$
is obtained by gluing $X$![]() and $Y$
and $Y$![]() along $A$
along $A$![]() . If $X$
. If $X$![]() and $Y$
and $Y$![]() are manifolds with $\partial X= \partial Y$
are manifolds with $\partial X= \partial Y$![]() , we also write $X\cup _\partial Y$
, we also write $X\cup _\partial Y$![]() to denote the gluing along their common boundary.
to denote the gluing along their common boundary.
Suppose that $M$![]() is a compact, oriented manifold of even dimension that is split as
is a compact, oriented manifold of even dimension that is split as
along a properly embedded submanifold $X_0$![]() of codimension $1$
of codimension $1$![]() , which is allowed to have boundary $\Sigma$
, which is allowed to have boundary $\Sigma$![]() . Let $X_1:=\partial M_1 \setminus \operatorname { {int}}(X_0)$
. Let $X_1:=\partial M_1 \setminus \operatorname { {int}}(X_0)$![]() and $X_2:=\partial M_2 \setminus \operatorname { {int}}(X_0)$
and $X_2:=\partial M_2 \setminus \operatorname { {int}}(X_0)$![]() . As unoriented manifolds, we have then $\partial X_0=\partial X_1 =\partial X_2 = \Sigma$
. As unoriented manifolds, we have then $\partial X_0=\partial X_1 =\partial X_2 = \Sigma$![]() and
and

We pick on $X_1$![]() the orientation coming from being a codimension $0$
the orientation coming from being a codimension $0$![]() submanifold of $\partial M_1$
submanifold of $\partial M_1$![]() , and we give $\Sigma$
, and we give $\Sigma$![]() the orientation coming from being the boundary of $X_1$
the orientation coming from being the boundary of $X_1$![]() . Suppose now that $\alpha \colon \pi _1(M)\to U(n)$
. Suppose now that $\alpha \colon \pi _1(M)\to U(n)$![]() is a representation. In our setting, $\Sigma$
is a representation. In our setting, $\Sigma$![]() is (up to orientation) the common boundary of $X_0$
is (up to orientation) the common boundary of $X_0$![]() , $X_1$
, $X_1$![]() and $X_2$
and $X_2$![]() , so that the canonical Lagrangians $V_{X_0}^{\alpha }$
, so that the canonical Lagrangians $V_{X_0}^{\alpha }$![]() , $V_{X_1}^{\alpha }$
, $V_{X_1}^{\alpha }$![]() and $V_{X_2}^{\alpha }$
and $V_{X_2}^{\alpha }$![]() all live in the same space $H_{k}(\Sigma ;\mathbb {C}^{n}_\alpha )$
all live in the same space $H_{k}(\Sigma ;\mathbb {C}^{n}_\alpha )$![]() . In particular, it makes sense to compute their Maslov triple index. In fact, the following result holds.
. In particular, it makes sense to compute their Maslov triple index. In fact, the following result holds.
Theorem 3.7 Wall's non-additivity
Let $M$![]() be a closed, oriented, even-dimensional manifold, and let $\alpha \colon \pi _1(M)\to U(n)$
be a closed, oriented, even-dimensional manifold, and let $\alpha \colon \pi _1(M)\to U(n)$![]() be a representation. Then, if $M$
be a representation. Then, if $M$![]() decomposes as $M=M_1\cup _{X_0} M_2$
decomposes as $M=M_1\cup _{X_0} M_2$![]() as above, we have
as above, we have
Remark 3.8 Theorem 3.7 was originally proved by Wall for the untwisted signature [Reference Wall30] (see also the paper of Py [Reference Py27, (3.2)] for a more detailed proof), and it can be easily checked that the result extends to twisted signatures. See [Reference Conway, Nagel and Toffoli12–Reference Degtyarev, Florens and Lecuona14] for further references and uses of the twisted version of the theorem.
3.4. The cut-and-paste formula for the rho invariant
Suppose to have a closed, oriented $(2k+1)$![]() -dimensional manifold that is split by a codimension-one closed manifold $\Sigma$
-dimensional manifold that is split by a codimension-one closed manifold $\Sigma$![]() , yielding a decomposition $X_1\cup _\Sigma X_2$
, yielding a decomposition $X_1\cup _\Sigma X_2$![]() . Let $X_0$
. Let $X_0$![]() be a compact, oriented manifold with $\partial X_0=-\Sigma$
be a compact, oriented manifold with $\partial X_0=-\Sigma$![]() . Then, we can replace $X_1\cup _\Sigma X_2$
. Then, we can replace $X_1\cup _\Sigma X_2$![]() with the disjoint union of $X_1\cup _\Sigma X_0$
with the disjoint union of $X_1\cup _\Sigma X_0$![]() and $-X_0\cup _\Sigma X_2$
and $-X_0\cup _\Sigma X_2$![]() . We will call this manipulation cut-and-paste. Schematically, we have
. We will call this manipulation cut-and-paste. Schematically, we have
and pictorially we can represent the operation as in the next figure.

Suppose now that $\alpha \colon \pi _1(X_1\cup _\Sigma X_2)\to U(n)$![]() is a representation. In particular, $\alpha$
is a representation. In particular, $\alpha$![]() is defined on $\pi _1(X_1)$
is defined on $\pi _1(X_1)$![]() and on $\pi _1(\Sigma )$
and on $\pi _1(\Sigma )$![]() . In order to have rho invariants of $X_1 \cup _\Sigma X_0$
. In order to have rho invariants of $X_1 \cup _\Sigma X_0$![]() and $-X_0\cup _\Sigma X_2$
and $-X_0\cup _\Sigma X_2$![]() to be compared to $\rho _\alpha (X_1\cup _\Sigma X_2)$
to be compared to $\rho _\alpha (X_1\cup _\Sigma X_2)$![]() , we need to extend $\alpha$
, we need to extend $\alpha$![]() to the fundamental groups of these manifolds. This is possible if and only if we can construct an extension of $\alpha$
to the fundamental groups of these manifolds. This is possible if and only if we can construct an extension of $\alpha$![]() from $\pi _1(\Sigma )$
from $\pi _1(\Sigma )$![]() to $\pi _1(X_0)$
to $\pi _1(X_0)$![]() : then, using Seifert–Van Kampen's theorem, this will be patched with $\alpha \colon \pi _1(X_1)\to U(n)$
: then, using Seifert–Van Kampen's theorem, this will be patched with $\alpha \colon \pi _1(X_1)\to U(n)$![]() to produce representations $\pi _1(X_1 \cup _\Sigma X_0)\to U(n)$
to produce representations $\pi _1(X_1 \cup _\Sigma X_0)\to U(n)$![]() and $\pi _1(-X_0\cup _\Sigma X_2)\to U(n)$
and $\pi _1(-X_0\cup _\Sigma X_2)\to U(n)$![]() . For simplicity, we will use the same notation $\alpha$
. For simplicity, we will use the same notation $\alpha$![]() for all of these representations. Then, we want to compute the correction term $C$
for all of these representations. Then, we want to compute the correction term $C$![]() in the formula
in the formula
Now, if $X_1\cup _\Sigma X_0$![]() and $-X_0\cup _\Sigma X_2$
and $-X_0\cup _\Sigma X_2$![]() bound manifolds $W_1$
bound manifolds $W_1$![]() and $W_2$
and $W_2$![]() such that the representation extends, then Wall's theorem, together with the Atiyah–Patodi–Singer signature theorem, tells us how to compute the correction term. Namely, in that case, we have
such that the representation extends, then Wall's theorem, together with the Atiyah–Patodi–Singer signature theorem, tells us how to compute the correction term. Namely, in that case, we have
The content of the main result of this section is that the correction term $C$![]() of (3.2) is always given by (3.3), no matter whether the manifolds $W_1$
of (3.2) is always given by (3.3), no matter whether the manifolds $W_1$![]() and $W_2$
and $W_2$![]() exist. This should be compared with an analogous result for the untwisted eta invariant [Reference Bunke5, 2.5].
exist. This should be compared with an analogous result for the untwisted eta invariant [Reference Bunke5, 2.5].
Theorem 3.9 Let $X_1,$![]() $X_2$
$X_2$![]() and $X_0$
and $X_0$![]() be compact, oriented manifolds of dimension $2k+1$
be compact, oriented manifolds of dimension $2k+1$![]() with $\partial X_1=-\partial X_0=-\partial X_2=:\Sigma,$
with $\partial X_1=-\partial X_0=-\partial X_2=:\Sigma,$![]() and let $\alpha \colon \pi _1(X_1\cup _\partial X_2)\to U(n)$
and let $\alpha \colon \pi _1(X_1\cup _\partial X_2)\to U(n)$![]() be a representation that extends to $\pi _1(X_0)$
be a representation that extends to $\pi _1(X_0)$![]() . Then, for every choice of such an extension, we have
. Then, for every choice of such an extension, we have
where
with the first Maslov triple index performed on $H_{k}(\partial X_1;\mathbb {C}^{n}_\alpha ),$![]() and the second on $H_{k}(\partial X_1;\mathbb {C})$
and the second on $H_{k}(\partial X_1;\mathbb {C})$![]() .
.
Proof. Consider the oriented manifolds
We glue then $M_1$![]() with $M_2$
with $M_2$![]() along $\{1\}\times X_0$
along $\{1\}\times X_0$![]() , obtaining a topological oriented manifold $M$
, obtaining a topological oriented manifold $M$![]() to which $\alpha$
to which $\alpha$![]() extends.
extends.

The boundary of $M$![]() can be described topologically as
can be described topologically as
and we can equip $M$![]() with a smooth structure such that (3.4) is satisfied in the smooth sense [Reference tom Dieck29, 15.10.3]. Thanks to Theorem 2.6 (ii), we have then
with a smooth structure such that (3.4) is satisfied in the smooth sense [Reference tom Dieck29, 15.10.3]. Thanks to Theorem 2.6 (ii), we have then
By (3.4), the left-hand term is given by
By Wall's non-additivity (Theorem 3.7), we can compute the twisted and untwisted signature of $M$![]() as
as
The manifolds $M_1$![]() and $M_2$
and $M_2$![]() are of the form $[0,\,1]\times X$
are of the form $[0,\,1]\times X$![]() , with $X$
, with $X$![]() a closed manifold. In particular, they admit an orientation-reversing self-diffeomorphism defined by
a closed manifold. In particular, they admit an orientation-reversing self-diffeomorphism defined by
As orientation-reversing diffeomorphisms have the effect of changing sign to the signature, this shows that the ordinary signatures of $M_1$![]() and $M_2$
and $M_2$![]() vanish. Since the above diffeomorphism is trivial on the fundamental group, the same argument can be applied to the twisted signatures, which therefore also vanish. The computation of $\sigma (M)$
vanish. Since the above diffeomorphism is trivial on the fundamental group, the same argument can be applied to the twisted signatures, which therefore also vanish. The computation of $\sigma (M)$![]() and $\sigma _\alpha (M)$
and $\sigma _\alpha (M)$![]() is hence reduced to
is hence reduced to
Substituting (3.6) and (3.7) into (3.5), we get the desired formula.
Remark 3.10 An alternative approach to proving Theorem 3.9 would be by using gluing formulas for rho invariants for manifolds with boundary, as defined by Kirk and Lesch [Reference Kirk and Lesch20, Reference Kirk and Lesch21] (the discussion in [Reference Kirk and Lesch21, Section 8.3] might be hinting in this direction). This approach allows to prove the cut-and-paste formula at the level of eta invariants, leading to a slightly stronger result, albeit at the cost of more sophisticated tools to be introduced. See [Reference Toffoli28, Section 2.3.4] for details about this point of view.
4. Signatures of links and rho invariants
In § 4.1, we introduce rationally framed links and set up some notation and easy results. In § 4.2, we introduce the multivariable signatures of Cimasoni and Florens and recall a four-dimensional description for them. In § 4.3, we prove Proposition 4.18, which reinterprets the multivariable signature of a coloured link as the rho invariants of some closed three-manifold associated with the link. In § 4.4, we prove Theorem 4.24, which is a formula relating the multivariable signature of a link with the rho invariant of the three manifolds obtained by integer surgery on the link. In § 4.5, we prove Theorem 4.31, which under some additional hypotheses does the same for rational surgery.
Remark 4.1 In this section, given a manifold $X$![]() , we will only deal with one-dimensional unitary representations of $\pi _1(X)$
, we will only deal with one-dimensional unitary representations of $\pi _1(X)$![]() . As $U(1)$
. As $U(1)$![]() is an abelian group, every representation $\alpha '\colon \pi _1(X)\to U(1)$
is an abelian group, every representation $\alpha '\colon \pi _1(X)\to U(1)$![]() factors through the abelianization $\operatorname { {ab}}\colon \pi _1(X)\to H_1(X;\mathbb {Z})$
factors through the abelianization $\operatorname { {ab}}\colon \pi _1(X)\to H_1(X;\mathbb {Z})$![]() , and we can thus focus on representations $\alpha \colon H_1(X;\mathbb {Z})\to U(1)$
, and we can thus focus on representations $\alpha \colon H_1(X;\mathbb {Z})\to U(1)$![]() . We will normally write $\rho _\alpha$
. We will normally write $\rho _\alpha$![]() and $H_\alpha$
and $H_\alpha$![]() to denote rho invariants and twisted homology associated with the representation $\alpha '=\alpha \circ \operatorname { {ab}}$
to denote rho invariants and twisted homology associated with the representation $\alpha '=\alpha \circ \operatorname { {ab}}$![]() .
.
Remark 4.2 A straightforward computation in twisted homology leads to the following well-known fact: for the two-dimensional torus $T^{2}$![]() , we have $H_*(T^{2};\mathbb {C}^{n}_\alpha )=0$
, we have $H_*(T^{2};\mathbb {C}^{n}_\alpha )=0$![]() for all non-trivial representation $\alpha \colon H_1(T;\mathbb {Z})\to U(1)$
for all non-trivial representation $\alpha \colon H_1(T;\mathbb {Z})\to U(1)$![]() . In this section, we will always use Theorem 3.9 in the situation where $\Sigma$
. In this section, we will always use Theorem 3.9 in the situation where $\Sigma$![]() is a disjoint union of two-dimensional tori and where the restriction of $\alpha$
is a disjoint union of two-dimensional tori and where the restriction of $\alpha$![]() to the first homology of these is non-trivial. As a consequence, the Maslov triple index in twisted homology will always be $0$
to the first homology of these is non-trivial. As a consequence, the Maslov triple index in twisted homology will always be $0$![]() .
.
4.1. Links and framings
Let $L=K_1\cup \cdots \cup K_k$![]() be an oriented link in $S^{3}$
be an oriented link in $S^{3}$![]() (from now on, just a link). By removing from $S^{3}$
(from now on, just a link). By removing from $S^{3}$![]() the interior of a closed tubular neighbourhood $N(L)$
the interior of a closed tubular neighbourhood $N(L)$![]() , we get its link exterior
, we get its link exterior
The link exterior $X_L$![]() is a compact, oriented three-manifold, whose boundary is a union of tori: to each link component $K_i\subseteq L$
is a compact, oriented three-manifold, whose boundary is a union of tori: to each link component $K_i\subseteq L$![]() , there corresponds a boundary component $T_i=-\partial (N(K_i))$
, there corresponds a boundary component $T_i=-\partial (N(K_i))$![]() (this is the orientation coming from being part of the boundary of $X_L$
(this is the orientation coming from being part of the boundary of $X_L$![]() , and it is the one we shall always consider). The link component $K_i$
, and it is the one we shall always consider). The link component $K_i$![]() determines the following two elements:
determines the following two elements:
• the meridian of $K_i$
 is the only element $\mu _i\in H_1(T_i;\mathbb {Z})$
is the only element $\mu _i\in H_1(T_i;\mathbb {Z})$ whose image in $H_1(N(K_i);\mathbb {Z})$
whose image in $H_1(N(K_i);\mathbb {Z})$ is $0$
is $0$ and such that $\operatorname { {lk}} (\mu _i,\, K_i)=1$
and such that $\operatorname { {lk}} (\mu _i,\, K_i)=1$ ;
;• the standard longitude of $K_i$
 is the only element $\lambda _i^{s}\in H_1(T_i;\mathbb {Z})$
is the only element $\lambda _i^{s}\in H_1(T_i;\mathbb {Z})$ whose image in $H_1(N(K_i);\mathbb {Z})$
whose image in $H_1(N(K_i);\mathbb {Z})$ is homologous to $K_i$
is homologous to $K_i$ and such that $\operatorname { {lk}} (\lambda _i^{s},\, K_i)=0$
and such that $\operatorname { {lk}} (\lambda _i^{s},\, K_i)=0$ .
.
For a knot $K$![]() , we shall often just use the notation $T$
, we shall often just use the notation $T$![]() , $\mu$
, $\mu$![]() and $\lambda$
and $\lambda$![]() for the boundary torus, the meridian and the standard longitude. Observe that the algebraic intersection of these two elements is given by
for the boundary torus, the meridian and the standard longitude. Observe that the algebraic intersection of these two elements is given by
We shall often consider the images of the above elements into homology with rational or complex coefficients without changing their names.
Definition 4.3 A rational framing on a link $L=K_1\cup \cdots \cup K_k$![]() is a $k$
is a $k$![]() -tuple of rational numbers $r=(r_1,\,\dotsc,\, r_k)$
-tuple of rational numbers $r=(r_1,\,\dotsc,\, r_k)$![]() . The pair $(L,\,r)$
. The pair $(L,\,r)$![]() is called a rationally framed link. If all $r_i$
is called a rationally framed link. If all $r_i$![]() 's are integers, we say that $r$
's are integers, we say that $r$![]() is an integer framing. The framed longitudes of a rationally framed link $(L,\,r)$
is an integer framing. The framed longitudes of a rationally framed link $(L,\,r)$![]() are the elements
are the elements
Without changing notation for them, we shall now consider the images of the meridians and framed longitudes in the homology of the link complement $X_L$![]() . It is an elementary well-known fact that $H_1(X_L;\mathbb {Z})$
. It is an elementary well-known fact that $H_1(X_L;\mathbb {Z})$![]() is a free $\mathbb {Z}$
is a free $\mathbb {Z}$![]() -module generated by the meridians, and that each standard longitude satisfies
-module generated by the meridians, and that each standard longitude satisfies
Next, we define the following matrix associated with a rationally framed link.
Definition 4.4 The framed linking matrix of a framed $k$![]() -component link $(L,\,r)$
-component link $(L,\,r)$![]() is the symmetric matrix $\Lambda _r=(\Lambda _{ij})_{i,j}\in \mathbb {Q}^{k\times k}$
is the symmetric matrix $\Lambda _r=(\Lambda _{ij})_{i,j}\in \mathbb {Q}^{k\times k}$![]() defined by
defined by

Example 4.5 The Seifert framing on a link $L=K_1\cup \cdots \cup K_k$![]() is the integer framing $(f_1,\, \cdots,\, f_k)$
is the integer framing $(f_1,\, \cdots,\, f_k)$![]() defined by
defined by
In particular, the coefficients of its framed linking matrix satisfy
The framed longitudes $\lambda _i=\lambda _i^{s} + f_i\mu _i$![]() associated with the Seifert framing correspond to the intersections of a Seifert surface with the boundary tori $T_i$
associated with the Seifert framing correspond to the intersections of a Seifert surface with the boundary tori $T_i$![]() .
.
From (4.2), together with the definition of the framed longitudes and of the framed linking matrix, it follows now immediately that the framed longitudes in the rational homology of $X_L$![]() are equal to
are equal to

For the computations involving the Maslov triple index, a good understanding of the complex symplectic space $H_1(\partial X_L;\mathbb {C})$![]() is required. The next result summarizes some easy facts that we will need later.
is required. The next result summarizes some easy facts that we will need later.
Lemma 4.6 Let $(L,\,r)$![]() be a $k$
be a $k$![]() -component rationally framed link. Then:
-component rationally framed link. Then:
(i) the collection $\{\mu _1,\, \dotsc \mu _k,\, \, \lambda _1,\, \dotsc \lambda _k\}$
 forms a basis for $H_1(\partial X_L;\mathbb {C})$
forms a basis for $H_1(\partial X_L;\mathbb {C})$ which satisfies
\[ \begin{cases} \mu_i\cdot\mu_j=\lambda_i\cdot\lambda_j=0,\\ \mu_i\cdot \lambda_j ={-}\delta_{ij} \end{cases} \quad \text{for all }i,j; \]
which satisfies
\[ \begin{cases} \mu_i\cdot\mu_j=\lambda_i\cdot\lambda_j=0,\\ \mu_i\cdot \lambda_j ={-}\delta_{ij} \end{cases} \quad \text{for all }i,j; \]
(ii) the canonical Lagrangian $V_{X_L}$
 can be described explicitly as
\[ V_{X_L}= {\operatorname{Span}}_\mathbb{C}\{v_1, \dotsc, v_k \}, \quad \text{where } v_i=\lambda_i - \sum_{s=1}^{k}\Lambda_{is} \mu_s; \]
can be described explicitly as
\[ V_{X_L}= {\operatorname{Span}}_\mathbb{C}\{v_1, \dotsc, v_k \}, \quad \text{where } v_i=\lambda_i - \sum_{s=1}^{k}\Lambda_{is} \mu_s; \]
(iii) the subspaces $\mathcal {M}:=\operatorname { {Span}}_\mathbb {C}\{\mu _1,\,\dotsc,\, \mu _k\}$
 and $\mathcal {L}_r=\operatorname { {Span}}_\mathbb {C}\{\lambda _1,\,\dotsc,\, \lambda _k\}$
and $\mathcal {L}_r=\operatorname { {Span}}_\mathbb {C}\{\lambda _1,\,\dotsc,\, \lambda _k\}$ are Lagran-gians, and their triple Maslov index with the canonical Lagrangian is given by
\[ \tau(\mathcal{M}, \mathcal{L}_r, V_{X_L})={\operatorname{sign}} \Lambda_r. \]
are Lagran-gians, and their triple Maslov index with the canonical Lagrangian is given by
\[ \tau(\mathcal{M}, \mathcal{L}_r, V_{X_L})={\operatorname{sign}} \Lambda_r. \]
Proof. $(i)$![]() is an immediate consequence of the definition of the framed meridians together with (4.1). $(ii)$
is an immediate consequence of the definition of the framed meridians together with (4.1). $(ii)$![]() is an immediate consequence of (4.3). The fact that $\mathcal {M}$
is an immediate consequence of (4.3). The fact that $\mathcal {M}$![]() and $\mathcal {L}_r$
and $\mathcal {L}_r$![]() are Lagrangians is obvious from $(i)$
are Lagrangians is obvious from $(i)$![]() . In order to prove $(iii)$
. In order to prove $(iii)$![]() , we compute the Maslov triple index using the definition. As $\mathcal {M}$
, we compute the Maslov triple index using the definition. As $\mathcal {M}$![]() and $\mathcal {L}_r$
and $\mathcal {L}_r$![]() are transverse, we have $(\mathcal {M} + \mathcal {L}_r)\cap V_{X_L} = V_{X_L}$
are transverse, we have $(\mathcal {M} + \mathcal {L}_r)\cap V_{X_L} = V_{X_L}$![]() , and every generator $v_i$
, and every generator $v_i$![]() can be written in a unique, obvious way as the sum of an element in $\mathcal {M}$
can be written in a unique, obvious way as the sum of an element in $\mathcal {M}$![]() and one in $\mathcal {L}_r$
and one in $\mathcal {L}_r$![]() . By Definition 3.1, then, $\tau (\mathcal {M},\, \mathcal {L}_r,\, V_{X_L})$
. By Definition 3.1, then, $\tau (\mathcal {M},\, \mathcal {L}_r,\, V_{X_L})$![]() is the signature of the Hermitian form $\psi \colon V_{X_L}\times V_{X_L}\to \mathbb {C}$
is the signature of the Hermitian form $\psi \colon V_{X_L}\times V_{X_L}\to \mathbb {C}$![]() defined on the basis elements of $V_{X_L}$
defined on the basis elements of $V_{X_L}$![]() by
by

It follows that $\tau (\mathcal {M},\, \mathcal {L}_r,\, V_{X_L})= \operatorname { {sign}} \Lambda _r$![]() , as it was desired.
, as it was desired.
Given a rationally framed link $(L,\,r)$![]() , we can consider the closed manifold $S_L(r)$
, we can consider the closed manifold $S_L(r)$![]() obtained by the Dehn surgery along the framing. This is done in the following way: for each link component $K_i$
obtained by the Dehn surgery along the framing. This is done in the following way: for each link component $K_i$![]() , we choose coprime integers $(p_i,\,q_i)$
, we choose coprime integers $(p_i,\,q_i)$![]() such that $p_i/q_i=r_i$
such that $p_i/q_i=r_i$![]() , and glue a solid torus $Y_i$
, and glue a solid torus $Y_i$![]() to $X_L$
to $X_L$![]() along the boundary component $T_i$
along the boundary component $T_i$![]() in such a way that the meridian of the solid torus is identified with the element $p_i\mu _i+q_i\lambda _i^{s}\in H_1(T_i;\mathbb {Z})$
in such a way that the meridian of the solid torus is identified with the element $p_i\mu _i+q_i\lambda _i^{s}\in H_1(T_i;\mathbb {Z})$![]() . In particular, $H_1(S_L(r);\mathbb {Z})$
. In particular, $H_1(S_L(r);\mathbb {Z})$![]() can be described as a quotient of $H_1(X_L;\mathbb {Z})$
can be described as a quotient of $H_1(X_L;\mathbb {Z})$![]() .
.
Definition 4.7 Given a link $L$![]() with a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
with a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() , we say that a rational framing $r$
, we say that a rational framing $r$![]() on $L$
on $L$![]() is compatible with $\alpha$
is compatible with $\alpha$![]() if $\alpha$
if $\alpha$![]() factors through $H_1(S_L(r);\mathbb {Z})$
factors through $H_1(S_L(r);\mathbb {Z})$![]() .
.
Remark 4.8 From the definition of surgery, it is clear that a rational framing $r=(r_1,\,\dotsc,\, r_k)$![]() with $r_i=p_i/q_i$
with $r_i=p_i/q_i$![]() as above is compatible with $\alpha$
as above is compatible with $\alpha$![]() if and only if $\alpha (p_i\mu _i+q_i\lambda _i^{s})=1$
if and only if $\alpha (p_i\mu _i+q_i\lambda _i^{s})=1$![]() for all $i$
for all $i$![]() . Using (4.2), we see that in terms of the coefficients of the framed linking matrix we have
. Using (4.2), we see that in terms of the coefficients of the framed linking matrix we have

Note that, in general, given a representation $\alpha$![]() , there might be no rational framing that is compatible with it.
, there might be no rational framing that is compatible with it.
4.2. Coloured links and signatures
A $n$![]() -colouring on a link $L$
-colouring on a link $L$![]() , for $n\in \mathbb {N}$
, for $n\in \mathbb {N}$![]() , is a partition of its components into $n$
, is a partition of its components into $n$![]() non-empty sublinks. Given a $k$
non-empty sublinks. Given a $k$![]() -component link $L=K_1\cup \cdots \cup K_k$
-component link $L=K_1\cup \cdots \cup K_k$![]() , we identify the colouring with a surjective function $c\colon \{1,\, \dotsc,\, k\}\to \{1,\, \dotsc,\, n\}$
, we identify the colouring with a surjective function $c\colon \{1,\, \dotsc,\, k\}\to \{1,\, \dotsc,\, n\}$![]() . The latter is the set of colours, and for every $1\leq s\leq n$
. The latter is the set of colours, and for every $1\leq s\leq n$![]() , we define
, we define
to be the sublink of colour $s$![]() . The pair $(L,\,c)$
. The pair $(L,\,c)$![]() is called an $n$
is called an $n$![]() -coloured link. We shall systematically omit $c$
-coloured link. We shall systematically omit $c$![]() (which has to be considered as fixed) and simply call $L$
(which has to be considered as fixed) and simply call $L$![]() an $n$
an $n$![]() -coloured link.
-coloured link.
Notation 4.9 For $n\in \mathbb {N}$![]() , set $\mathbb {T}^{n}:=(U(1))^{n}$
, set $\mathbb {T}^{n}:=(U(1))^{n}$![]() and $\mathbb {T}_*^{n}:=(U(1)\setminus \{1\})^{n}$
and $\mathbb {T}_*^{n}:=(U(1)\setminus \{1\})^{n}$![]() .
.
Using a generalization of the concept of Seifert surfaces (called C-complexes), Cimasoni and Florens defined a multivariable version of the Levine–Tristram signature of a link [Reference Cimasoni and Florens9]. Given an $n$![]() -coloured link $L$
-coloured link $L$![]() , their multivariable signature is a function
, their multivariable signature is a function
which coincides for $n=1$![]() with the Levine–Tristram signature function. We recall now the following four-dimensional description of the multivariable signature. We first need a definition.
with the Levine–Tristram signature function. We recall now the following four-dimensional description of the multivariable signature. We first need a definition.
Definition 4.10 A bounding surface for an $n$![]() -coloured link $L$
-coloured link $L$![]() is a union $F = F_1\cup \cdots \cup F_n$
is a union $F = F_1\cup \cdots \cup F_n$![]() of properly embedded, locally flat, compact, oriented surfaces $F_i \subseteq D^{4}$
of properly embedded, locally flat, compact, oriented surfaces $F_i \subseteq D^{4}$![]() with $\partial F_i = L_i\in \partial D^{4}=S^{3}$
with $\partial F_i = L_i\in \partial D^{4}=S^{3}$![]() and that only intersect each other transversally in double points.
and that only intersect each other transversally in double points.
A bounding surface for $L$![]() can be obtained for example by pushing the interior of a C-complex into the interior of $D^{4}$
can be obtained for example by pushing the interior of a C-complex into the interior of $D^{4}$![]() (see e.g. [Reference Conway, Friedl and Toffoli10, Section 3] for details). Given a bounding surface $F=F_1\cup \cdots \cup F_n\subseteq D^{4}$
(see e.g. [Reference Conway, Friedl and Toffoli10, Section 3] for details). Given a bounding surface $F=F_1\cup \cdots \cup F_n\subseteq D^{4}$![]() for a link $L$
for a link $L$![]() , we can take a small tubular neighbourhood $N(F_i)$
, we can take a small tubular neighbourhood $N(F_i)$![]() of each surface $F_i$
of each surface $F_i$![]() and define the exterior of $F$
and define the exterior of $F$![]() in $D^{4}$
in $D^{4}$![]() as the four-manifold with boundary
as the four-manifold with boundary
It is easy to show that $H_1(W_F;\mathbb {Z})$![]() is freely generated by the meridians of the surfaces $F_1,\, \dotsc,\, F_n$
is freely generated by the meridians of the surfaces $F_1,\, \dotsc,\, F_n$![]() (the meridian of $F_i$
(the meridian of $F_i$![]() being the image in $H_1(W_F;\mathbb {Z})$
being the image in $H_1(W_F;\mathbb {Z})$![]() of any of the meridians of $L_i$
of any of the meridians of $L_i$![]() ). The following description of the Cimasoni–Florens signature is known [Reference Conway, Nagel and Toffoli12, Proposition 3.5].
). The following description of the Cimasoni–Florens signature is known [Reference Conway, Nagel and Toffoli12, Proposition 3.5].
Proposition 4.11 Let $L$![]() be a an $n$
be a an $n$![]() -coloured link in $S^{3}$
-coloured link in $S^{3}$![]() and let $F=F_1\cup \cdots \cup F_n$
and let $F=F_1\cup \cdots \cup F_n$![]() be a bounding surface for $L$
be a bounding surface for $L$![]() . Let $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}_*^{n}$
. Let $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(W_F;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(W_F;\mathbb {Z})\to U(1)$![]() be the representation that sends the meridian of $F_i$
be the representation that sends the meridian of $F_i$![]() to $\omega _i$
to $\omega _i$![]() . Then, we have
. Then, we have
We conclude this part with a couple of definitions.
Definition 4.12 Let $L=K_1\cup \cdots \cup K_k$![]() be an $n$
be an $n$![]() -coloured link. The coloured Seifert framing on $L$
-coloured link. The coloured Seifert framing on $L$![]() is the integer framing $f_L=(f_1,\,\dotsc,\, f_k)$
is the integer framing $f_L=(f_1,\,\dotsc,\, f_k)$![]() given by
given by

In other words, it is the framing obtained by providing each coloured sublink $L_i$![]() with its Seifert framing (see e.g. 4.5).
with its Seifert framing (see e.g. 4.5).
Observe that the coloured Seifert framing on $L$![]() needs not coincide with the Seifert framing of the underlying link. In fact, its framed longitudes correspond to the intersection of $\partial X_L$
needs not coincide with the Seifert framing of the underlying link. In fact, its framed longitudes correspond to the intersection of $\partial X_L$![]() with a C-complex. From the definition of the coloured Seifert framing, it is immediate to see that the coefficients of the associated framed linking matrix satisfy
with a C-complex. From the definition of the coloured Seifert framing, it is immediate to see that the coefficients of the associated framed linking matrix satisfy

Definition 4.13 Given an $n$![]() -coloured link $L$
-coloured link $L$![]() , a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, a representation $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() is said to be coloured if it sends meridians of the same colour to the same value, i.e. if
is said to be coloured if it sends meridians of the same colour to the same value, i.e. if
Given an element $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}^{n}$![]() , the coloured representation $\alpha$
, the coloured representation $\alpha$![]() defined by $\alpha (\mu _i):=\omega _{c(i)}$
defined by $\alpha (\mu _i):=\omega _{c(i)}$![]() is said to be the representation associated to $\omega$
is said to be the representation associated to $\omega$![]() .
.
It is immediate to see that the above association gives a natural bijection between elements $\omega =(\omega _1,\, \dotsc,\, \omega _n)\in \mathbb {T}^{n}$![]() and coloured representations $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
and coloured representations $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() .
.
4.3. Multivariable signatures as rho invariants
As the untwisted signature of $W_F$![]() is $0$
is $0$![]() (see for example [Reference Conway, Nagel and Toffoli12, Proposition 3.3]), Proposition 4.11 is equivalent to the formula
(see for example [Reference Conway, Nagel and Toffoli12, Proposition 3.3]), Proposition 4.11 is equivalent to the formula
In particular, by the Atiyah–Patodi–Singer theorem, we have
We will give now a more explicit description of $\partial W_F$![]() , and see how to replace it with a manifold which is independent of the choice of $F$
, and see how to replace it with a manifold which is independent of the choice of $F$![]() .
.
We start by recalling the following construction, which is a special case of plumbing. Let $\Gamma$![]() be a graph whose set of vertices is $\{1,\,\dotsc,\, n\}$
be a graph whose set of vertices is $\{1,\,\dotsc,\, n\}$![]() and such that:
and such that:
• each vertex $i$
 is decorated by a compact, oriented surface $\Sigma _i$
is decorated by a compact, oriented surface $\Sigma _i$ (or, equivalently, by pair of natural numbers $[g_i,\,r_i]$
(or, equivalently, by pair of natural numbers $[g_i,\,r_i]$ corresponding to the genus and number of boundary components of $\Sigma _i$
corresponding to the genus and number of boundary components of $\Sigma _i$ );
);• each edge is decorated by a number $\varepsilon =\pm 1$
 .
.
In the following, we shall refer to a graph with the decorations described above as a plumbing graph. We construct then an oriented three-manifold $P_\Gamma$![]() by the following process.
by the following process.
(1) For each edge with endpoints $i$
 and $j$
and $j$ , remove a small open disk from $\Sigma _i$
, remove a small open disk from $\Sigma _i$ and one from $\Sigma _j$
and one from $\Sigma _j$ . Let $\Sigma _1',\, \dotsc,\, \Sigma _j'$
. Let $\Sigma _1',\, \dotsc,\, \Sigma _j'$ be the resulting surfaces.
be the resulting surfaces.(2) For each edge with endpoints $i$
 and $j$
and $j$ and decoration $\varepsilon =\pm 1$
and decoration $\varepsilon =\pm 1$ , glue the three-manifolds $\Sigma _i'\times S^{1}$
, glue the three-manifolds $\Sigma _i'\times S^{1}$ and $\Sigma _j'\times S^{1}$
and $\Sigma _j'\times S^{1}$ along the boundary components coming from the two corresponding removed disks, according to the diffeomorphism $\varphi \colon S^{1}\times S^{1} \to S^{1}\times S^{1}$
along the boundary components coming from the two corresponding removed disks, according to the diffeomorphism $\varphi \colon S^{1}\times S^{1} \to S^{1}\times S^{1}$ given by $\varphi (x,\,y)= (y^{\varepsilon },\,x^{\varepsilon })$
given by $\varphi (x,\,y)= (y^{\varepsilon },\,x^{\varepsilon })$ .
.(3) Set
\[ P_\Gamma:=\Big(\bigsqcup_{i=1}^{n} \Sigma_i'\times S^{1} \Big)\,/\!\sim, \]where $\sim$
 is the equivalence relation given by the above gluings.
is the equivalence relation given by the above gluings.
This construction coincides with that of [Reference Conway, Nagel and Toffoli12, Section 4]. With respect to the general plumbing construction [Reference Neumann26], it corresponds to the special case of all Euler numbers equal to $0$![]() , and our definition of plumbing graph also reflects this specialization. The boundary of $P_\Gamma$
, and our definition of plumbing graph also reflects this specialization. The boundary of $P_\Gamma$![]() is a disjoint union of $r=\sum \nolimits _i r_i$
is a disjoint union of $r=\sum \nolimits _i r_i$![]() tori. These tori maintain a preferred product structure, and we can describe the boundary of $P_\Gamma$
tori. These tori maintain a preferred product structure, and we can describe the boundary of $P_\Gamma$![]() as
as

As in [Reference Conway, Nagel and Toffoli12], we give the following definition.
Definition 4.14 Given a plumbing graph $\Gamma$![]() , the total weight of a pair of vertices $\{s,\,t\}$
, the total weight of a pair of vertices $\{s,\,t\}$![]() , denoted by $p_\Gamma (s,\,t)$
, denoted by $p_\Gamma (s,\,t)$![]() , is the integer obtained as the sum of the $\pm 1$
, is the integer obtained as the sum of the $\pm 1$![]() -decorations of all the edges with endpoints $s$
-decorations of all the edges with endpoints $s$![]() and $t$
and $t$![]() . If all total weights of $\Gamma$
. If all total weights of $\Gamma$![]() are $0$
are $0$![]() , the plumbing graph $\Gamma$
, the plumbing graph $\Gamma$![]() is called balanced.
is called balanced.
Example 4.15 Let $F=F_1\cup \cdots \cup F_n\subseteq D^{4}$![]() be a bounding surface for $L$
be a bounding surface for $L$![]() . The boundary of $W_F$
. The boundary of $W_F$![]() then is given up to orientation-preserving diffeomorphism as
then is given up to orientation-preserving diffeomorphism as
where $\Gamma _F$![]() is a graph whose vertices $\{1,\, \dotsc,\, n\}$
is a graph whose vertices $\{1,\, \dotsc,\, n\}$![]() are decorated by the surfaces $F_i$
are decorated by the surfaces $F_i$![]() 's, and whose edges correspond to the intersection points between them, with the sign of the intersection as decoration (see [Reference Conway, Nagel and Toffoli12, Example 4.12]). Observe that the total weights of $\Gamma _F$
's, and whose edges correspond to the intersection points between them, with the sign of the intersection as decoration (see [Reference Conway, Nagel and Toffoli12, Example 4.12]). Observe that the total weights of $\Gamma _F$![]() are given by
are given by
The boundary of $-P_{\Gamma _F}$![]() , which can be described as in (4.6), is identified in the gluing (4.7) with $\partial X_L$
, which can be described as in (4.6), is identified in the gluing (4.7) with $\partial X_L$![]() as follows. The boundary piece $-\partial F_s\times S^{1}$
as follows. The boundary piece $-\partial F_s\times S^{1}$![]() is identified with the boundary tori of colour $s$
is identified with the boundary tori of colour $s$![]() in $\partial X_L$
in $\partial X_L$![]() , in such a way that:
, in such a way that:
(1) the classes of the $S^{1}$
 -factors are glued to the meridians;
-factors are glued to the meridians;(2) the classes of the boundary components of $F_s$
 are glued to the framed longitudes associated with the coloured Seifert framing.
are glued to the framed longitudes associated with the coloured Seifert framing.
As we have seen in (4.5), the multivariable signature of $L$![]() can be expressed up to sign as the rho invariant of $\partial W_F$
can be expressed up to sign as the rho invariant of $\partial W_F$![]() . In turn, as it appears from Example 4.15, $\partial W_F$
. In turn, as it appears from Example 4.15, $\partial W_F$![]() can be described as the union of $X_L$
can be described as the union of $X_L$![]() with some plumbed three-manifold which depends on the choice of a bounding surface for $L$
with some plumbed three-manifold which depends on the choice of a bounding surface for $L$![]() . In the next construction, we will build a plumbing graph $\Gamma _L$
. In the next construction, we will build a plumbing graph $\Gamma _L$![]() associated with $L$
associated with $L$![]() . The associated closed three-manifold $Y_L$
. The associated closed three-manifold $Y_L$![]() , obtained by gluing $P_{\Gamma _L}$
, obtained by gluing $P_{\Gamma _L}$![]() with $X_L$
with $X_L$![]() , will play the role of $\partial W_F$
, will play the role of $\partial W_F$![]() with the advantage of being unequivocally determined by the link $L$
with the advantage of being unequivocally determined by the link $L$![]() .
.
Notation 4.16 Given a link $L$![]() in $S^{3}$
in $S^{3}$![]() , let $\left |{L}\right |\in \mathbb {N}$
, let $\left |{L}\right |\in \mathbb {N}$![]() be its number of components.
be its number of components.
Construction 4.17 Given an $n$![]() -coloured link $L$
-coloured link $L$![]() , we construct the associated plumbing graph $\Gamma _L$
, we construct the associated plumbing graph $\Gamma _L$![]() in the following way:
in the following way:
• the set of vertices is $\{1,\,\dotsc n\}$
 , and the vertex $i$
, and the vertex $i$ is decorated by a genus-0 surface with $\left |{L_i}\right |$
is decorated by a genus-0 surface with $\left |{L_i}\right |$ boundary components;
boundary components;• between each pair of distinct vertices $i,\,j$
 there are exactly $\left |{\operatorname { {lk}} (L_i,\,L_j)}\right |$
there are exactly $\left |{\operatorname { {lk}} (L_i,\,L_j)}\right |$ edges, and they are all decorated by $\varepsilon =\operatorname { {sign}}(\operatorname { {lk}} (L_i,\,L_j))$
edges, and they are all decorated by $\varepsilon =\operatorname { {sign}}(\operatorname { {lk}} (L_i,\,L_j))$ .
.
In other words, we are plumbing spheres with the appropriate number of punctures along the smallest graph $\Gamma$![]() whose total weights satisfy the condition $p_{\Gamma }(i,\,j)= \operatorname { {lk}}(L_i,\,L_j)$
whose total weights satisfy the condition $p_{\Gamma }(i,\,j)= \operatorname { {lk}}(L_i,\,L_j)$![]() . Then, we form a closed three-manifold $Y_L$
. Then, we form a closed three-manifold $Y_L$![]() as
as
The identification along the boundary is defined in the exact same way as the one arising in Example 4.15, i.e. identifying the classes corresponding to the $S^{1}$![]() -factors of $-\partial P_{\Gamma _L}$
-factors of $-\partial P_{\Gamma _L}$![]() with the meridians of $L$
with the meridians of $L$![]() of the appropriate colour, and the classes corresponding to the boundary components of the punctured sphere with the longitudes associated with the coloured Seifert framing.
of the appropriate colour, and the classes corresponding to the boundary components of the punctured sphere with the longitudes associated with the coloured Seifert framing.
Using some of the ideas of [Reference Conway, Nagel and Toffoli12] together with the cut-and-paste formula of § 2, we will now show that the multivariable signature can be written as the rho invariant of $Y_L$![]() .
.
Proposition 4.18 Let $L$![]() be an $n$
be an $n$![]() -coloured link. Let $\omega \in \mathbb {T}_*^{n},$
-coloured link. Let $\omega \in \mathbb {T}_*^{n},$![]() and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Then, $\alpha$
be the associated coloured representation. Then, $\alpha$![]() can be extended to a representation of $H_1(Y_L;\mathbb {Z})$
can be extended to a representation of $H_1(Y_L;\mathbb {Z})$![]() and, for any choice of an extension, we have
and, for any choice of an extension, we have
Proof. Let $F=F_1\cup \cdots \cup F_n\subseteq D^{4}$![]() be a bounding surface for $L$
be a bounding surface for $L$![]() . Then, as $\alpha$
. Then, as $\alpha$![]() is a coloured representation, it extends to a representation $H_1(W_F;\mathbb {Z})\to U(1)$
is a coloured representation, it extends to a representation $H_1(W_F;\mathbb {Z})\to U(1)$![]() that, for all colour $s$
that, for all colour $s$![]() , sends the meridian of $F_s$
, sends the meridian of $F_s$![]() to $\omega _s\in U(1)$
to $\omega _s\in U(1)$![]() . By (4.5), we have hence
. By (4.5), we have hence
As we have seen in Example 4.15, we have $\partial W_F=X_L\cup _\partial (-P_{\Gamma _F})$![]() , where $\Gamma _F$
, where $\Gamma _F$![]() is a plumbing graph determined by $F$
is a plumbing graph determined by $F$![]() . We perform now cut-and-paste by replacing $P_{\Gamma _F}$
. We perform now cut-and-paste by replacing $P_{\Gamma _F}$![]() with $P_{\Gamma _L}$
with $P_{\Gamma _L}$![]() . Schematically, this is
. Schematically, this is
The manifold $P_{\Gamma _L}\cup _\partial (-P_{\Gamma _F})$![]() can be seen as the plumbing along the graph $\Gamma$
can be seen as the plumbing along the graph $\Gamma$![]() whose vertices $\{1,\, \dotsc,\, n\}$
whose vertices $\{1,\, \dotsc,\, n\}$![]() are decorated by the closed surfaces $\Sigma _s\cup _\partial (-F_s)$
are decorated by the closed surfaces $\Sigma _s\cup _\partial (-F_s)$![]() and whose set of edges is the union of all edges of $\Gamma _L$
and whose set of edges is the union of all edges of $\Gamma _L$![]() and $\Gamma _F$
and $\Gamma _F$![]() , with the decorations of the edges of $\Gamma _F$
, with the decorations of the edges of $\Gamma _F$![]() changed of sign. In particular, (4.9) can be rewritten as
changed of sign. In particular, (4.9) can be rewritten as
Observe that, by construction, for each pair of vertices $\{s,\,t\}$![]() we have
we have
so that
i.e. $\Gamma$![]() is balanced.
is balanced.
We will now prove that the representation $\alpha$![]() can be extended to $H_1(Y_L;\mathbb {Z})$
can be extended to $H_1(Y_L;\mathbb {Z})$![]() . In the gluings, the boundary of $X_L$
. In the gluings, the boundary of $X_L$![]() is identified with the boundaries of $P_{\Gamma _F}$
is identified with the boundaries of $P_{\Gamma _F}$![]() and $P_{\Gamma _L}$
and $P_{\Gamma _L}$![]() , leading to natural maps
, leading to natural maps
induced by the inclusions. Standard Mayer–Vietoris computations, together with the equality (4.11), show that $\ker \varphi$![]() and $\ker \psi$
and $\ker \psi$![]() coincide, as both are generated by the following elements (compare with [Reference Conway, Nagel and Toffoli12, Lemma 4.7]):
coincide, as both are generated by the following elements (compare with [Reference Conway, Nagel and Toffoli12, Lemma 4.7]):
(i) the differences $\mu _i-\mu _j$
 with $c(i)=c(j)$
with $c(i)=c(j)$ ;
;(ii) for each colour $s$
 , the element
\[ \sum_{c(i)=s}\ \lambda_i - \sum_{t\ne s}{\operatorname{lk}}(L_s,L_t)\mu_{j_t}, \]where $\mu _{j_t}$
, the element
\[ \sum_{c(i)=s}\ \lambda_i - \sum_{t\ne s}{\operatorname{lk}}(L_s,L_t)\mu_{j_t}, \]where $\mu _{j_t}$
 is any meridian of colour $t$
is any meridian of colour $t$ .
.
As $\alpha$![]() extends to $H_1(W_F;\mathbb {Z})$
extends to $H_1(W_F;\mathbb {Z})$![]() , it is also defined on $H_1(\partial W_F;\mathbb {Z})=H_1(P_{\Gamma _F};\mathbb {Z})$
, it is also defined on $H_1(\partial W_F;\mathbb {Z})=H_1(P_{\Gamma _F};\mathbb {Z})$![]() . In particular, $\alpha$
. In particular, $\alpha$![]() has to be trivial on $\ker \varphi$
has to be trivial on $\ker \varphi$![]() (this can be verified using the explicit description of the generators). From the fact that $\ker \varphi =\ker \psi$
(this can be verified using the explicit description of the generators). From the fact that $\ker \varphi =\ker \psi$![]() , we see then that $\alpha$
, we see then that $\alpha$![]() also admits an extension to $H_1(P_{\Gamma _L};\mathbb {Z})$
also admits an extension to $H_1(P_{\Gamma _L};\mathbb {Z})$![]() , because $U(1)$
, because $U(1)$![]() is divisible.
is divisible.
Pick any extension $\alpha \colon H_1(P_{\Gamma _L};\mathbb {Z})\to U(1)$![]() of $\alpha$
of $\alpha$![]() . We can now apply the cut-and-paste formula of Theorem 3.9 to (4.10), obtaining
. We can now apply the cut-and-paste formula of Theorem 3.9 to (4.10), obtaining
(the Maslov triple index in twisted homology is $0$![]() because all $\omega _i$
because all $\omega _i$![]() 's are non-trivial by assumption; see Remark 4.2). As we have seen, the plumbing graph $\Gamma$
's are non-trivial by assumption; see Remark 4.2). As we have seen, the plumbing graph $\Gamma$![]() is balanced. As a consequence, we have $\rho _\alpha (P_{\Gamma })=0$
is balanced. As a consequence, we have $\rho _\alpha (P_{\Gamma })=0$![]() by a computation of Conway, Nagel and the author [Reference Conway, Nagel and Toffoli12, Proposition 4.10]. The Lagrangians $V_{P_{\Gamma _F}}$
by a computation of Conway, Nagel and the author [Reference Conway, Nagel and Toffoli12, Proposition 4.10]. The Lagrangians $V_{P_{\Gamma _F}}$![]() and $V_{P_{\Gamma _L}}$
and $V_{P_{\Gamma _L}}$![]() are identified under the gluing to
are identified under the gluing to
where $\varphi$![]() and $\psi$
and $\psi$![]() are the maps defined in (4.12). From the fact that $\ker \varphi =\ker \psi$
are the maps defined in (4.12). From the fact that $\ker \varphi =\ker \psi$![]() it follows then that $V_{P_{\Gamma _F}}=V_{P_\Gamma }$
it follows then that $V_{P_{\Gamma _F}}=V_{P_\Gamma }$![]() , and hence we have $\tau (V_{X_L},\,V_{P_{\Gamma _F}},\, V_{P_{\Gamma _L}})=0$
, and hence we have $\tau (V_{X_L},\,V_{P_{\Gamma _F}},\, V_{P_{\Gamma _L}})=0$![]() . The equality (4.13) gets thus rewritten as
. The equality (4.13) gets thus rewritten as
Substituting this into (4.8), the proof is complete.
We introduce now the following definitions.
Definition 4.19 Let $L=K_1\cup \cdots \cup K_k$![]() be an $n$
be an $n$![]() -coloured link. Then
-coloured link. Then
(i) if $\operatorname { {lk}}(L_s,\,L_t)=0$
 for all pairs $(s,\,t)$
for all pairs $(s,\,t)$ of distinct colours, we say that $L$
of distinct colours, we say that $L$ is colour-to-colour algebraically split;
is colour-to-colour algebraically split;(ii) if every link component $K_i$
 satisfies $\operatorname { {lk}}(K_i,\, L_s)=0$
satisfies $\operatorname { {lk}}(K_i,\, L_s)=0$ for all $s\ne c(i)$
for all $s\ne c(i)$ , we say that $L$
, we say that $L$ is component-to-colour algebraically split.
is component-to-colour algebraically split.
Of course, being component-to-colour algebraically split is a stronger condition than being colour-to-colour algebraically split. Any onecoloured link is component-to-colour algebraically split, and so is any link with vanishing linking numbers, no matter what colouring it is assigned.
Remark 4.20 If $L$![]() is colour-to-colour algebraically split, then $Y_L$
is colour-to-colour algebraically split, then $Y_L$![]() has a very simple description. In fact, in this case, $\Gamma _L$
has a very simple description. In fact, in this case, $\Gamma _L$![]() is a graph with no edges, and thus the associated plumbed three-manifold is
is a graph with no edges, and thus the associated plumbed three-manifold is

where $\Sigma _s$![]() is a sphere with $\left |{L_s}\right |$
is a sphere with $\left |{L_s}\right |$![]() punctures. As a consequence of Proposition 4.18, the multivariable signature is hence (up to sign) just the rho invariant of the closed three-manifold obtained by gluing these products $\Sigma _s\times S^{1}$
punctures. As a consequence of Proposition 4.18, the multivariable signature is hence (up to sign) just the rho invariant of the closed three-manifold obtained by gluing these products $\Sigma _s\times S^{1}$![]() to the link exterior $X_L$
to the link exterior $X_L$![]() . This holds, in particular, if $L$
. This holds, in particular, if $L$![]() is onecoloured, so that we can always express the Levine–Tristram signature of $L$
is onecoloured, so that we can always express the Levine–Tristram signature of $L$![]() as
as
where $\Sigma$![]() is a punctured sphere. In the case of a knot, this gives the well-known description of the Levine–Tristram signature as the rho invariant of the manifold obtained by $0$
is a punctured sphere. In the case of a knot, this gives the well-known description of the Levine–Tristram signature as the rho invariant of the manifold obtained by $0$![]() -framed surgery. In the next two sections, we will study the relationship between rho invariants and the Dehn surgery in higher generality.
-framed surgery. In the next two sections, we will study the relationship between rho invariants and the Dehn surgery in higher generality.
4.4. Integral surgery
We will now study the value of the rho invariant of manifolds obtained by integral surgery on a link $L$![]() . We start by recalling the following result of Cimasoni and Florens [Reference Cimasoni and Florens9, Theorem 6.7].
. We start by recalling the following result of Cimasoni and Florens [Reference Cimasoni and Florens9, Theorem 6.7].
Theorem 4.21 Cimasoni–Florens
Let $L$![]() be a $k$
be a $k$![]() -coloured $k$
-coloured $k$![]() -component link. Let $q\in \mathbb {N}$
-component link. Let $q\in \mathbb {N}$![]() a positive integer and let $n_1,\,\dotsc,\, n_k\in \{1,\,\dotsc,\, p-1\}$
a positive integer and let $n_1,\,\dotsc,\, n_k\in \{1,\,\dotsc,\, p-1\}$![]() be integers, each of which is coprime with $q$
be integers, each of which is coprime with $q$![]() . Let $\omega =(e^{2\pi in _1/q},\, \dotsc,\, e^{2\pi i n_k/q})\in (S^{1}\setminus \{1\})^{n}$
. Let $\omega =(e^{2\pi in _1/q},\, \dotsc,\, e^{2\pi i n_k/q})\in (S^{1}\setminus \{1\})^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Let $g$
be the associated coloured representation. Let $g$![]() be a compatible integral framing on $L$
be a compatible integral framing on $L$![]() . Then, we have
. Then, we have

Remark 4.22 The result of Cimasoni and Florens was originally written in terms of the Casson–Gordon invariant of § 2.3. We have translated it into a result about the rho invariant by using Proposition 2.8.
Remark 4.23 Observe that formulas about any colouring of $L$![]() can be extracted from Theorem 4.21, as the signature function associated with any colouring can be easily deduced from the one associated with the maximal colouring [Reference Cimasoni and Florens9, Proposition 2.5]. For the onecolouring, this gives back a result of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1] about the Levine–Tristram signature.
can be extracted from Theorem 4.21, as the signature function associated with any colouring can be easily deduced from the one associated with the maximal colouring [Reference Cimasoni and Florens9, Proposition 2.5]. For the onecolouring, this gives back a result of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1] about the Levine–Tristram signature.
We would like to remove the restrictions on the values of $\omega$![]() in the statement of Theorem 4.21. In order to be able to do so, we need to assume some conditions about the linking numbers between components of different colours.
in the statement of Theorem 4.21. In order to be able to do so, we need to assume some conditions about the linking numbers between components of different colours.
The main result of this section is the following, which holds in the case of colour-to-colour algebraically split links.
Theorem 4.24 Let $L$![]() be an $n$
be an $n$![]() -coloured link which is colour-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$
-coloured link which is colour-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n}$![]() , and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
, and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Let $g$
be the associated coloured representation. Let $g$![]() be a compatible integral framing on $L$
be a compatible integral framing on $L$![]() . Then, we have
. Then, we have

where, for each colour $s,$![]() $\theta _s\in (0,\,1)$
$\theta _s\in (0,\,1)$![]() is such that $\omega _s=e^{2\pi i \theta _s},$
is such that $\omega _s=e^{2\pi i \theta _s},$![]() and $h_s$
and $h_s$![]() is the sum of all the coefficients of the framed linking matrix of the sublink $L_s$
is the sum of all the coefficients of the framed linking matrix of the sublink $L_s$![]() .
.
Proof. Set $P:=P_{\Gamma _L}$![]() . Let $k$
. Let $k$![]() be the number of components of $L$
be the number of components of $L$![]() . We perform the cut-and-paste illustrated schematically by
. We perform the cut-and-paste illustrated schematically by
where $Y=Y_1\sqcup \cdots \sqcup Y_k$![]() is a disjoint union of $k$
is a disjoint union of $k$![]() solid tori, glued along the framing $g$
solid tori, glued along the framing $g$![]() , and $P$
, and $P$![]() is glued as prescribed by Construction 4.17. As $L$
is glued as prescribed by Construction 4.17. As $L$![]() is colour-to-colour algebraically split, by Remark 4.20, we have
is colour-to-colour algebraically split, by Remark 4.20, we have

where, for each colour $s$![]() , $\Sigma _s$
, $\Sigma _s$![]() is a sphere with $\left |{L_s}\right |$
is a sphere with $\left |{L_s}\right |$![]() punctures. The manifold $P\cup _\partial Y$
punctures. The manifold $P\cup _\partial Y$![]() is thus the disjoint union of the $n$
is thus the disjoint union of the $n$![]() closed manifolds obtained by capping all of the $\Sigma _s\times S^{1}$
closed manifolds obtained by capping all of the $\Sigma _s\times S^{1}$![]() 's appropriately with solid tori.
's appropriately with solid tori.
Claim 1 Up to an orientation-preserving diffeomorphism, we have

in such a way that the element $1\in \mathbb {Z}/h_s=\pi _1(L(h_s,\,1))$![]() is given by the class $[S^{1}]\in H_1(\Sigma _s\times S^{1};\mathbb {Z})$
is given by the class $[S^{1}]\in H_1(\Sigma _s\times S^{1};\mathbb {Z})$![]() .
.
We postpone for the moment the proof of this claim. As a consequence of Claim 1, (4.14) can be rewritten up to orientation-preserving diffeomorphism as

Observe that the restriction of $\alpha$![]() to $H_1(\Sigma _s\times S^{1})$
to $H_1(\Sigma _s\times S^{1})$![]() sends the class $[S^{1}]$
sends the class $[S^{1}]$![]() to $\omega _s$
to $\omega _s$![]() , as the boundary circles of the form $\{p_i\}\times S^{1}$
, as the boundary circles of the form $\{p_i\}\times S^{1}$![]() are identified with the meridians of the link. The representation $\alpha$
are identified with the meridians of the link. The representation $\alpha$![]() extends thus to $L(h_s,\,1)$
extends thus to $L(h_s,\,1)$![]() in such a way that, for each colour $s$
in such a way that, for each colour $s$![]() , the element $1\in \mathbb {Z}/h_s=H_1(L(h_s,\,1);\mathbb {Z}))$
, the element $1\in \mathbb {Z}/h_s=H_1(L(h_s,\,1);\mathbb {Z}))$![]() is sent to $\omega _s$
is sent to $\omega _s$![]() . We can now apply Theorem 3.9 and get
. We can now apply Theorem 3.9 and get

(as usual, there is no Maslov triple index in twisted cohomology because of Remark 4.2). The first summand in the right-hand term of (4.15) is minus the multivariable signature of $L$![]() thanks to Proposition 4.18. Using Corollary 2.11 to describe the rho invariant of the lens spaces at hand, and swapping the second and third variables of the Maslov triple index (see Proposition 3.2 (i)), we can rewrite (4.15) as
thanks to Proposition 4.18. Using Corollary 2.11 to describe the rho invariant of the lens spaces at hand, and swapping the second and third variables of the Maslov triple index (see Proposition 3.2 (i)), we can rewrite (4.15) as

Hence, in order to conclude, we need to identify the Maslov triple index term in (4.16). The rest of the proof is devoted to this.
Instead of trying to calculate the Maslov triple index directly, we use the cocycle property of our three Lagrangians together with $\mathcal {M}:=\operatorname { {Span}}_\mathbb {C}\{\mu _1,\,\dotsc,\, \mu _k\}$![]() to simplify this task. Namely, using Proposition 3.2 (ii), we find
to simplify this task. Namely, using Proposition 3.2 (ii), we find
We set the following notation. Let $\lambda _1,\,\dotsc,\, \lambda _k$![]() be the framed longitudes associated with the surgery framing $g=(g_1,\,\dotsc,\, g_k)$
be the framed longitudes associated with the surgery framing $g=(g_1,\,\dotsc,\, g_k)$![]() , and let $\lambda _1,\,\dotsc,\, \lambda _k$
, and let $\lambda _1,\,\dotsc,\, \lambda _k$![]() bet the framed longitudes associated with the coloured Seifert framing $f_L=(f_1,\,\dotsc,\, f_k)$
bet the framed longitudes associated with the coloured Seifert framing $f_L=(f_1,\,\dotsc,\, f_k)$![]() . By definition, then, we have
. By definition, then, we have
We also use the notation $\Lambda _{ij}$![]() for the coefficients of the framed linking matrix $\Lambda _g$
for the coefficients of the framed linking matrix $\Lambda _g$![]() , and $\Lambda _{ij}'$
, and $\Lambda _{ij}'$![]() for those of the frame linking matrix $\Lambda _{f_L}$
for those of the frame linking matrix $\Lambda _{f_L}$![]() (these two matrices only differ on the diagonal). We have the following description of the four Lagrangian subspaces appearing in the right-hand term of (4.17):
(these two matrices only differ on the diagonal). We have the following description of the four Lagrangian subspaces appearing in the right-hand term of (4.17):

We compute now the three summands separately. We will prove the following.
Claim 2 $\tau (\mathcal {M},\,V_P,\, V_Y)=-\sum \nolimits _{s=1}^{n}\operatorname { {sgn}}(h_s)$![]() .
.
Claim 3 $\tau (\mathcal {M},\, V_P,\, V_{X_L})=0$![]() .
.
Claim 4 $\tau (\mathcal {M},\, V_Y,\, V_{X_L})=\operatorname { {sign}}(\Lambda _g)$![]() .
.
These three claims, together with (4.16) and (4.17), lead to the desired formula. In order to conclude, we are only left with proving Claim 1 to 4.
Proof of Claim 2. Write $\tau (\mathcal {M},\,V_P,\, V_Y)=\tau (V_Y,\,\mathcal {M},\,V_P)$![]() . Clearly, we have
. Clearly, we have
In fact, the generators of $V_P$![]() of the form $\mu _i-\mu _j$
of the form $\mu _i-\mu _j$![]() are in $\mathcal {M}$
are in $\mathcal {M}$![]() , and the generators $v_s$
, and the generators $v_s$![]() can be written as
can be written as
where the first summand is in $V_Y$![]() , and the second summand is in $\mathcal {M}$
, and the second summand is in $\mathcal {M}$![]() . Let
. Let
be the Hermitian form associated with the triple $(V_Y,\,\mathcal {M},\,V_P)$![]() , whose signature is $\tau (V_Y,\,\mathcal {M},\,V_P)$
, whose signature is $\tau (V_Y,\,\mathcal {M},\,V_P)$![]() . The generators of the form $\mu _i-\mu _j$
. The generators of the form $\mu _i-\mu _j$![]() are clearly in the radical of $\psi$
are clearly in the radical of $\psi$![]() , as they belong to the Lagrangian $\mathcal {M}$
, as they belong to the Lagrangian $\mathcal {M}$![]() . As a consequence, it is enough to study $\psi$
. As a consequence, it is enough to study $\psi$![]() on the span of $v_1,\, \dotsc,\, v_n$
on the span of $v_1,\, \dotsc,\, v_n$![]() . Using the definition of $\psi$
. Using the definition of $\psi$![]() and the decomposition (4.19), we compute
and the decomposition (4.19), we compute

As a consequence, we have

By definition of the coloured Seifert framing, together with the fact that $g_i=\Lambda _{ii}$![]() , we can now compute that, for each colour $s$
, we can now compute that, for each colour $s$![]() , we have
, we have

Putting these computations together, we find the equation in the statement of the claim.
Proof of Claim 3. The space $(\mathcal {M}+V_P)\cap V_{X_L}$![]() is the $n$
is the $n$![]() -dimensional subspace generated by the terms
-dimensional subspace generated by the terms

where the first summand is in $\mathcal {M}$![]() and the second summand is in $V_P$
and the second summand is in $V_P$![]() . Let
. Let
be the Hermitian form associated with the triple $(\mathcal {M},\, V_P,\, V_{X_L})$![]() . Then, from the decomposition (4.20), we can compute
. Then, from the decomposition (4.20), we can compute

For $s=t$![]() , this is $0$
, this is $0$![]() by definition of the coloured Seifert framing. For $s\ne t$
by definition of the coloured Seifert framing. For $s\ne t$![]() , instead, it is equal to $\operatorname { {lk}}(L_s,\,L_t)$
, instead, it is equal to $\operatorname { {lk}}(L_s,\,L_t)$![]() , which is $0$
, which is $0$![]() because the link is colour-to-colour algebraically split. In particular, the form $\varphi$
because the link is colour-to-colour algebraically split. In particular, the form $\varphi$![]() is trivial and the Maslov triple index is $0$
is trivial and the Maslov triple index is $0$![]() as claimed.
as claimed.
Proof of Claim 4. This follows immediately from Lemma 4.6 (iii), as $V_Y=\mathcal {L}_g$![]() .
.
Proof of Claim 1. As we have observed, $P_{\Gamma _L}$![]() is the disjoint union of manifolds of the form $\Sigma _s\times S^{1}$
is the disjoint union of manifolds of the form $\Sigma _s\times S^{1}$![]() , where $\Sigma _s$
, where $\Sigma _s$![]() is a punctured sphere. By construction, in the gluing $X_L\cup _\partial Y$
is a punctured sphere. By construction, in the gluing $X_L\cup _\partial Y$![]() , the meridian $m_i$
, the meridian $m_i$![]() of the solid torus $Y_i$
of the solid torus $Y_i$![]() is identified with the framed longitude $\lambda _i$
is identified with the framed longitude $\lambda _i$![]() of the surgery framing $g$
of the surgery framing $g$![]() . On the other hand, when $-P_{\Gamma _L}$
. On the other hand, when $-P_{\Gamma _L}$![]() is glued to $X_L$
is glued to $X_L$![]() , a boundary component $C_i\times S^{1}\subseteq \partial \Sigma _s\times S^{1}$
, a boundary component $C_i\times S^{1}\subseteq \partial \Sigma _s\times S^{1}$![]() is identified with the boundary torus $K_i$
is identified with the boundary torus $K_i$![]() in such a way that, homologically, the class $[C_i]$
in such a way that, homologically, the class $[C_i]$![]() coincides with the framed longitude $\lambda _i'$
coincides with the framed longitude $\lambda _i'$![]() of the coloured Seifert framing, and $[S^{1}]$
of the coloured Seifert framing, and $[S^{1}]$![]() coincide with the meridian $\mu _i$
coincide with the meridian $\mu _i$![]() . The “by-product” gluing $P_{\Gamma _L}\cup _\partial Y$
. The “by-product” gluing $P_{\Gamma _L}\cup _\partial Y$![]() is the result of capping the boundary $\Sigma _s\times S^{1}$
is the result of capping the boundary $\Sigma _s\times S^{1}$![]() with solid tori. As a consequence of this and (4.18), these cappings are given by the identifications
with solid tori. As a consequence of this and (4.18), these cappings are given by the identifications
In particular, for each $s$![]() , this construction leads to the lens space $L(-h'_s,\, 1)$
, this construction leads to the lens space $L(-h'_s,\, 1)$![]() or equivalently to $-L(h_s',\,1)$
or equivalently to $-L(h_s',\,1)$![]() , with
, with
It is also easy to see that the element $1\in \mathbb {Z}/h_s'$![]() corresponds to $[S^{1}]$
corresponds to $[S^{1}]$![]() as desired. The proof is concluded by proving that $h_s'=h_s$
as desired. The proof is concluded by proving that $h_s'=h_s$![]() . This follows from the definition of the coloured Seifert framing and the sequence of equalities
. This follows from the definition of the coloured Seifert framing and the sequence of equalities

Remark 4.25 Applying Theorem 4.24 in the onecoloured setting, where the first hypothesis is always satisfied, we get the following formula relating the rho invariant of the manifold obtained by surgery and the Levine–Tristram signature:
where $\theta \in (0,\,1)$![]() is such that $\omega =e^{2\pi i\theta }$
is such that $\omega =e^{2\pi i\theta }$![]() and the sum is over the coefficients of $\Lambda _g$
and the sum is over the coefficients of $\Lambda _g$![]() . For $\theta \in \mathbb {Q}$
. For $\theta \in \mathbb {Q}$![]() , this coincides with a formula of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1].
, this coincides with a formula of Casson and Gordon [Reference Casson and Gordon7, Lemma 3.1].
Example 4.26 Let $r,\,s$![]() be positive coprime integers, and let $T(r,\,s)$
be positive coprime integers, and let $T(r,\,s)$![]() denote the $(r,\,s)$
denote the $(r,\,s)$![]() -torus knot. The $(rs-1)$
-torus knot. The $(rs-1)$![]() -Dehn surgery on $T(r,\,s)$
-Dehn surgery on $T(r,\,s)$![]() gives a manifold which is orientation-preserving diffeomorphic to the lens space $L(rs-1,\,s^{2})$
gives a manifold which is orientation-preserving diffeomorphic to the lens space $L(rs-1,\,s^{2})$![]() [Reference Moser24, Proposition 3.2]. Let $\zeta :=e^{2\pi i/(rs-1)}$
[Reference Moser24, Proposition 3.2]. Let $\zeta :=e^{2\pi i/(rs-1)}$![]() , and let $0\leq k \leq rs-2$
, and let $0\leq k \leq rs-2$![]() . Keeping track of the induced map on the fundamental group under this diffeomorphism, by (4.21) (applied with $\omega =\zeta ^{k}$
. Keeping track of the induced map on the fundamental group under this diffeomorphism, by (4.21) (applied with $\omega =\zeta ^{k}$![]() ) we obtain
) we obtain
It might be interesting to compare this formula to other known computations for the Levine–Tristram signature of torus knots (see e.g. the paper of Borodzik and Oleszkiewicz [Reference Borodzik and Oleszkiewicz4]).
Suppose now that the $n$![]() -coloured link $L$
-coloured link $L$![]() is component-to-colour algebraically split. Observe that, under this assumption, the coloured Seifert framing coincides with the usual Seifert framing, i.e. with the coloured Seifert framing associated with the onecolouring of the same underlying link. As explained by the next result, this framing has the important property of being compatible with all $U(1)$
is component-to-colour algebraically split. Observe that, under this assumption, the coloured Seifert framing coincides with the usual Seifert framing, i.e. with the coloured Seifert framing associated with the onecolouring of the same underlying link. As explained by the next result, this framing has the important property of being compatible with all $U(1)$![]() -representations of $H_1(X_L;\mathbb {Z})\to U(1)$
-representations of $H_1(X_L;\mathbb {Z})\to U(1)$![]() .
.
Lemma 4.27 Let $L$![]() be an $n$
be an $n$![]() -coloured link which is component-to-colour algebraically split. Then, the coloured Seifert framing $f_L$
-coloured link which is component-to-colour algebraically split. Then, the coloured Seifert framing $f_L$![]() is compatible with all coloured representations $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
is compatible with all coloured representations $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() .
.
Proof. By Remark 4.8, we need to prove that

Let $\omega \in \mathbb {T}^{n}$![]() be the element determined by the relations $\alpha (\mu _i)=\omega _{c(i)}$
be the element determined by the relations $\alpha (\mu _i)=\omega _{c(i)}$![]() for all $i$
for all $i$![]() . We can write then
. We can write then

Since $L$![]() is component-to-colour algebraically split, for every $s$
is component-to-colour algebraically split, for every $s$![]() different from $s_i:=c(i)$
different from $s_i:=c(i)$![]() we have
we have
As a consequence, (4.23) can be rewritten as

By (4.4), moreover, the exponent in the right-hand term of (4.24) is $0$![]() , and thus (4.22) is satisfied.
, and thus (4.22) is satisfied.
Corollary 4.28 Let $L$![]() be an $n$
be an $n$![]() -coloured link which is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n},$
-coloured link which is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n},$![]() and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$
and let $\alpha \colon H_1(X_L;\mathbb {Z})\to U(1)$![]() be the associated coloured representation. Then, $\alpha$
be the associated coloured representation. Then, $\alpha$![]() extends to $H_1(S_L(f_L);\mathbb {Z})$
extends to $H_1(S_L(f_L);\mathbb {Z})$![]() and we have
and we have
Proof. The representation $\alpha$![]() extends to $H_1(S_L(f_L);\mathbb {Z})$
extends to $H_1(S_L(f_L);\mathbb {Z})$![]() thanks to Lemma 4.27, so that we can apply Theorem 4.24. The desired formula follows then from the observation that, for the coloured Seifert framing, thanks to (4.4) for any colour $s$
thanks to Lemma 4.27, so that we can apply Theorem 4.24. The desired formula follows then from the observation that, for the coloured Seifert framing, thanks to (4.4) for any colour $s$![]() we have
we have
Remark 4.29 Both Lemma 4.27 and Corollary 4.28 hold in particular in the onecoloured setting, where they were proved by Nagel and Powell [Reference Nagel and Powell25, Section 5]. Our work is a generalization of this to the multivariable setting.
4.5. Rational surgery
We now want to study the rho invariant of the closed manifold obtained by surgery along a rational framing on a link. We start from the case of a knot, as the statement and the proof are a bit simpler in this setting. Observe that, for a knot $K$![]() , a representation $\psi \colon H_1(X_K)\to U(1)$
, a representation $\psi \colon H_1(X_K)\to U(1)$![]() , extends to $M_K(p/q)$
, extends to $M_K(p/q)$![]() if and only if $\psi (\mu )^{p}=1$
if and only if $\psi (\mu )^{p}=1$![]() , i.e. if and only if $\omega :=\psi (\mu )$
, i.e. if and only if $\omega :=\psi (\mu )$![]() is a $p$
is a $p$![]() th root of unity.
th root of unity.
Proposition 4.30 Let $K$![]() be a knot, and let $\alpha \colon H_1(X_K;\mathbb {Z})\to U(1)$
be a knot, and let $\alpha \colon H_1(X_K;\mathbb {Z})\to U(1)$![]() be the representation defined by $\alpha (\mu )=\omega,$
be the representation defined by $\alpha (\mu )=\omega,$![]() with $\omega$
with $\omega$![]() being a $p$
being a $p$![]() th root of unity. Then, we have
th root of unity. Then, we have
Proof. We perform cut-and-paste on $S_K(p/q)$![]() in the following way: we cut out the solid torus $Y=D^{2}\times S^{1}$
in the following way: we cut out the solid torus $Y=D^{2}\times S^{1}$![]() of the filling, and we replace it with another copy $Y'=D^{2}\times S^{1}$
of the filling, and we replace it with another copy $Y'=D^{2}\times S^{1}$![]() , this time glued along the $0$
, this time glued along the $0$![]() framing. It is convenient to actually glue $-Y'$
framing. It is convenient to actually glue $-Y'$![]() instead of $Y'$
instead of $Y'$![]() : in such a way, we can define an orientation-reversing diffeomorphism between $-\partial Y'$
: in such a way, we can define an orientation-reversing diffeomorphism between $-\partial Y'$![]() and $\partial X_K$
and $\partial X_K$![]() which gives the identifications
which gives the identifications
between the standard basis $(m',\,l')$![]() of $H_1(Y';\mathbb {Z})$
of $H_1(Y';\mathbb {Z})$![]() and the basis $(\mu,\, \lambda )$
and the basis $(\mu,\, \lambda )$![]() of $H_1(\partial X_L;\mathbb {Z})$
of $H_1(\partial X_L;\mathbb {Z})$![]() . On the other hand, the meridian $m$
. On the other hand, the meridian $m$![]() of $Y$
of $Y$![]() is identified with $p\mu +q\lambda$
is identified with $p\mu +q\lambda$![]() . Schematically, we write
. Schematically, we write
The union of solid tori $Y'\cup _\delta Y$![]() is now given along a diffeomorphism which gives the identification of $m$
is now given along a diffeomorphism which gives the identification of $m$![]() with $qm'+pl'$
with $qm'+pl'$![]() , so that the resulting manifold is the lens space $L(p,\,-q)\cong -L(p,\,q)$
, so that the resulting manifold is the lens space $L(p,\,-q)\cong -L(p,\,q)$![]() (see § 2.4). In particular, (4.25) can be rewritten as
(see § 2.4). In particular, (4.25) can be rewritten as
Observe that the generator $1\in \mathbb {Z}/p=\pi _1(L(p,\,q))$![]() corresponds by construction to the longitude $l'$
corresponds by construction to the longitude $l'$![]() . In turn, $l'$
. In turn, $l'$![]() is glued in the surgery with the meridian $\mu$
is glued in the surgery with the meridian $\mu$![]() of $K$
of $K$![]() . As a consequence, the extension of the representation $\alpha$
. As a consequence, the extension of the representation $\alpha$![]() to $H_1(L(p,\,q);\mathbb {Z})$
to $H_1(L(p,\,q);\mathbb {Z})$![]() is the representation $\mathbb {Z}/p\to U(1)$
is the representation $\mathbb {Z}/p\to U(1)$![]() given by $1\mapsto \omega$
given by $1\mapsto \omega$![]() . Before applying the cut-and-paste formula, we observe that the result is trivially true for $\omega =1$
. Before applying the cut-and-paste formula, we observe that the result is trivially true for $\omega =1$![]() . We shall hence suppose $\omega \ne 1$
. We shall hence suppose $\omega \ne 1$![]() . Thanks to Theorem 3.9, we can now compute
. Thanks to Theorem 3.9, we can now compute
(as usual, the Maslov triple index in twisted homology is $0$![]() thanks to Remark 4.2 and the assumption $\omega \ne 1$
thanks to Remark 4.2 and the assumption $\omega \ne 1$![]() ). Now, we know that the first summand in the right-hand term of (4.26) is minus the Levine–Tristram signature (see Remark 4.20), while the second summand coincides with the one of the statement. As a consequence, to complete the proof, it is enough to show that $\tau (V_{Y'},\, V_{X_K},\, V_Y)=0$
). Now, we know that the first summand in the right-hand term of (4.26) is minus the Levine–Tristram signature (see Remark 4.20), while the second summand coincides with the one of the statement. As a consequence, to complete the proof, it is enough to show that $\tau (V_{Y'},\, V_{X_K},\, V_Y)=0$![]() . We are going to describe the Lagrangians explicitly. Considering the identifications given by the gluings, in terms of the basis $(\mu,\,\lambda )$
. We are going to describe the Lagrangians explicitly. Considering the identifications given by the gluings, in terms of the basis $(\mu,\,\lambda )$![]() of $H_1(\partial X_K;\mathbb {C})$
of $H_1(\partial X_K;\mathbb {C})$![]() we have
we have
As the first two subspaces coincide, the Maslov triple index is $0$![]() , and the proof is complete.
, and the proof is complete.
We shall now prove the general version of Proposition 4.30, which holds for all component-to-colour algebraically split links. As we have seen, a special case of these are onecoloured links. In particular, this gives a general formula relating the Levine–Tristram signature of a link $L$![]() with the Atiyah–Patodi–Singer rho invariant of the closed three-manifold obtained by rational surgery on $L$
with the Atiyah–Patodi–Singer rho invariant of the closed three-manifold obtained by rational surgery on $L$![]() .
.
Theorem 4.31 Let $L$![]() be an $n$
be an $n$![]() -coloured, $k$
-coloured, $k$![]() -component link that is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n},$
-component link that is component-to-colour algebraically split. Let $\omega \in \mathbb {T}_*^{n},$![]() and let $\alpha \colon \pi _1(X_L)\to U(1)$
and let $\alpha \colon \pi _1(X_L)\to U(1)$![]() be the associated coloured representation. Let $r$
be the associated coloured representation. Let $r$![]() be a compatible rational framing on $L$
be a compatible rational framing on $L$![]() . Then, we have
. Then, we have

where $p_i,\,q_i$![]() are coprime integers such that $r_i-f_i=p_i/q_i$
are coprime integers such that $r_i-f_i=p_i/q_i$![]() (here, $f_i$
(here, $f_i$![]() is the $i$
is the $i$![]() -th coefficient of the Seifert framing).
-th coefficient of the Seifert framing).
Proof. We generalize the cut-and-paste construction of Proposition 4.30, removing the union of solid tori $Y$![]() coming from the $r$
coming from the $r$![]() -framed filling of $X_L$
-framed filling of $X_L$![]() , and replacing them with a union of solid tori $Y'$
, and replacing them with a union of solid tori $Y'$![]() glued along the coloured Seifert framing. As the difference between these framings is now given by the $k$
glued along the coloured Seifert framing. As the difference between these framings is now given by the $k$![]() -tuple $(p_1/q_1,\, \dotsc,\, p_k/q_k)$
-tuple $(p_1/q_1,\, \dotsc,\, p_k/q_k)$![]() , the same argument used in the proof of Proposition 4.30 (repeated now for each link component) implies that this cut-and-paste can be written as
, the same argument used in the proof of Proposition 4.30 (repeated now for each link component) implies that this cut-and-paste can be written as

In particular, Theorem 3.9 gives in this case

Applying Corollary 4.28 and rearranging the variables of the Maslov triple index with Proposition 3.2 (i), we can rewrite the last equation as

The computation of the Maslov triple index is more involved than in the case of knots. As we did in the proof of Theorem 4.24, instead of trying to calculate it directly, we use the cocycle property of our three Lagrangians together with $\mathcal {M}:=\{\mu _1,\,\dotsc,\, \mu _k\}$![]() to simplify this task. Namely, using Proposition 3.2 (ii), we find
to simplify this task. Namely, using Proposition 3.2 (ii), we find
Claim 1 $\tau (\mathcal {M},\,V_{Y'},\, V_Y)= -\sum \nolimits _{i=1}^{k} \operatorname { {sgn}}(p_i/q_i)$![]() .
.
Claim 2 $\tau (\mathcal {M},\, V_{Y'},\, V_{X_L})= \operatorname { {sign}}\Lambda _{f_L}$![]() and $\tau (\mathcal {M},\, V_Y,\, V_{X_L})=\operatorname { {sign}} \Lambda _r$
and $\tau (\mathcal {M},\, V_Y,\, V_{X_L})=\operatorname { {sign}} \Lambda _r$![]() .
.
Thanks to (4.28), the two claims (whose proof we postpone for the moment) combine to give

Substituting this value into (4.27), we obtain the formula in the statement of the theorem.
Proof of Claim 1. Let $\lambda _1,\,\dotsc,\, \lambda _k$![]() be the framed longitudes corresponding to the framing $r$
be the framed longitudes corresponding to the framing $r$![]() , and let $\lambda _1',\,\dotsc,\, \lambda _k'$
, and let $\lambda _1',\,\dotsc,\, \lambda _k'$![]() be the framed longitudes of the Seifert framing. Then, it is clear that
be the framed longitudes of the Seifert framing. Then, it is clear that
Moreover, by definition, we have $\lambda _i=\lambda _i^{s}+r_i\mu _i$![]() and $\lambda _i'=\lambda _i^{s}+f_i\mu _i$
and $\lambda _i'=\lambda _i^{s}+f_i\mu _i$![]() , so that the two sets of longitudes are related by
, so that the two sets of longitudes are related by
In particular, the three Lagrangians in the first summand of (4.28) all split according to the symplectic decomposition

As the pair $(\mu _i,\,\lambda _i')$![]() is a symplectic basis for $(H_1(T_i;\mathbb {C}),\, \cdot )$
is a symplectic basis for $(H_1(T_i;\mathbb {C}),\, \cdot )$![]() (see Example 3.3), it is immediate to compute
(see Example 3.3), it is immediate to compute

Proof of Claim 2. The claim follows immediately from Lemma 4.6 (iii), as we have $V_Y=\mathcal {L}_r$![]() and $V_{Y'}=\mathcal {L}_{f_L}$
and $V_{Y'}=\mathcal {L}_{f_L}$![]() .
.
Remark 4.32 The hypothesis of $L$![]() being component-to-colour algebraically split allows us to obtain a single nice explicit formula, because, in this case, we can always apply the cut-and-paste formula after performing the Dehn surgery along the Seifert framing, which is compatible with all representations thanks to Lemma 4.27. More general cases of rational surgery can be faced by finding an appropriate compatible integral framing (together with Theorem 4.21 or Theorem 4.24) and then modifying it into the desired rational framing in the same way as in the proof of Theorem 4.31. However, this is better dealt with on a case-by-case basis, as a general formula would be quite cumbersome.
being component-to-colour algebraically split allows us to obtain a single nice explicit formula, because, in this case, we can always apply the cut-and-paste formula after performing the Dehn surgery along the Seifert framing, which is compatible with all representations thanks to Lemma 4.27. More general cases of rational surgery can be faced by finding an appropriate compatible integral framing (together with Theorem 4.21 or Theorem 4.24) and then modifying it into the desired rational framing in the same way as in the proof of Theorem 4.31. However, this is better dealt with on a case-by-case basis, as a general formula would be quite cumbersome.
Remark 4.33 If $L$![]() is component-to-colour algebraically split and $g$
is component-to-colour algebraically split and $g$![]() is an integer framing on $L$
is an integer framing on $L$![]() which is compatible with the given $\omega \in \mathbb {T}_*^{n}$
which is compatible with the given $\omega \in \mathbb {T}_*^{n}$![]() , we can apply either Theorem 4.24 or Theorem 4.31. The fact that the resulting formulas are compatible can be verified by a quick computation using Corollary 2.11.
, we can apply either Theorem 4.24 or Theorem 4.31. The fact that the resulting formulas are compatible can be verified by a quick computation using Corollary 2.11.
Acknowledgements
This project was supported by the collaborative research center SFB 1085 ’Higher Invariants’, funded by the Deutsche Forschungsgemeinschaft. Part of the article is based on the author's PhD thesis, which was written under the support of the graduate school GRK 1692 ’Curvature, Cycles, and Cohomology’, also funded by the Deutsche Forschungsgemeinschaft. The author would like to thank Stefan Friedl for several interesting discussions.