Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T23:43:32.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Heavy-usage asymptotic expansions for the waiting time in closed processor-sharing systems with multiple classes

Published online by Cambridge University Press:  01 July 2016

J. A. Morrison  and
D. Mitra
J. A. Morrison*
Affiliation:
AT&T Bell Laboratories
D. Mitra*
Affiliation:
AT&T Bell Laboratories
*
∗Postal address: AT&T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974, USA.
∗Postal address: AT&T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We present new results based on novel techniques for the problem of characterizing the waiting-time distribution in a class of closed queueing networks in heavy usage, which in practical terms means that the processor is utilized more than about 80 per cent. This paper extends recent work by Mitra and Morrison [10] on the same system in normal usage. The closed system has a CPU operating under the processor-sharing (‘time-slicing’) discipline and a bank of terminals. The presence of multiple job-classes allows distinctions in the user’s behavior in the terminal and in the service requirements. This work is primarily applicable to the case of large numbers of terminals. We give an effective method for calculating, for the equilibrium waiting time, the first and second moments and the leading term in the asymptotic approximation to the distribution. 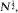Our results are in the form of asymptotic expansions in inverse powers of , where N is a large parameter. The expansion coefficients depend on the classical parabolic cylinder functions.

Keywords

QUEUEING NETWORKSQUEUEING THEORYRESIDENCE TIME
Type
Research Article
Information
Advances in Applied Probability , Volume 17 , Issue 1 , March 1985 , pp. 163 - 185
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. and Stegun, I. A. (1970) Handbook of Mathematical Functions. Dover, New York.Google Scholar
2. Coffman, E. G., Muniz, R. R. and Trotter, H. (1970) Waiting time distributions for processor-sharing systems. J. Assoc. Comput. Mach. 17, 123–130.CrossRefGoogle Scholar
3. Daduna, H. (1982) Passage times for overtake-free paths in Gordon-Newell networks. Adv. Appl. Prob. 14, 672–686.CrossRefGoogle Scholar
4. Kelly, F. P. and Pollett, P. K. (1983) Sojourn times in closed queueing networks. Adv. Appl. Prob. 15, 638–656.CrossRefGoogle Scholar
5. Mckenna, J., Mitra, D. and Ramakrishnan, K. G. (1981) A class of closed Markovian queuing networks: integral representations, asymptotic expansions and generalizations. Bell System Tech. J. 60, 599–641.CrossRefGoogle Scholar
6. Magnus, W., Oberhettinger, F and Soni, R. P. (1966) Formulas and Theorems for the Special Functions of Mathematical Physics. Springer-Verlag, New York.CrossRefGoogle Scholar
7. Melamed, B. (1982) Sojourn times in queueing networks. Math. Operat. Res. 7, 223–244.CrossRefGoogle Scholar
8. Mitra, D. (1982) Waiting time distributions from closed queueing network models of shared-processor systems. In Performance 81, ed. Kylstra, F. J., North-Holland, Amsterdam, 113–131.Google Scholar
9. Mitra, D. and Morrison, J. A. (1983) Asymptotic expansions of moments of the waiting time in a shared-processor of an interactive system. SIAM J. Computing 12, 789–802.CrossRefGoogle Scholar
10. Mitra, D. and Morrison, J. A. (1983) Asymptotic expansions of moments of the waiting time in closed and open processor-sharing systems with multiple job classes. Adv. Appl. Prob. 15, 813–839.CrossRefGoogle Scholar
11. Schassberger, R. (1984) Residence time in the M/G/1 processor-sharing queue. Adv. Appl. Prob. 16, 202–213.CrossRefGoogle Scholar