Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-21T05:55:17.966Z Has data issue: false hasContentIssue false
  • English
  • Français

High-order strongly nonlinear long wave approximation and solitary wave solution. Part 2. Internal waves

Published online by Cambridge University Press:  01 December 2022

Wooyoung Choi Open the ORCID record for Wooyoung Choi [Opens in a new window]
Wooyoung Choi*
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102-1982, USA
*
†Email address for correspondence: wychoi@njit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

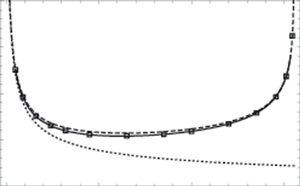
A strongly nonlinear long-wave approximation is adopted to obtain a high-order model for large-amplitude long internal waves in a two-layer system by assuming the water depth is much smaller than the typical wavelength. When truncated at the first order, the model can be reduced to the regularized strongly nonlinear model of Choi et al. (J. Fluid Mech., vol. 629, 2009, pp. 73–85), which lessens the Kelvin–Helmholtz instability excited by the tangential velocity jump across the interface in the inviscid Miyata–Choi–Camassa (MCC) equations. Using the second-order model, the next-order correction to the internal solitary wave solution of the MCC equations is found and its validity is examined with the Euler solution in terms of the wave profile, the effective wavelength and the velocity profile. It is shown that the correction greatly improves the comparison with the Euler solution for the whole range of wave amplitudes and no further correction is necessary for practical applications. Based on a local stability analysis, the region of stability for the second-order long-wave model is identified in the physical parameter space so that the efficient numerical scheme developed for the first-order model can be used for the second-order model.

JFM classification

Geophysical and Geological Flows: Internal waves Waves/Free-surface Flows: Solitary waves Geophysical and Geological Flows: Shallow water flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A41
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agnon, Y., Madsen, P.A. & Schaffer, H.A. 1999 A new approach to high-order Boussinesq models. J. Fluid Mech. 399, 319–333.CrossRefGoogle Scholar
Barros, R. & Choi, W. 2013 On regularizing the strongly nonlinear model for two-dimensional internal waves. Physica D 264, 27–34.CrossRefGoogle Scholar
Barros, R., Choi, W. & Milewski, P.A. 2020 Strongly nonlinear effects on internal solitary waves in three-layer flows. J. Fluid Mech. 883, A16.CrossRefGoogle Scholar
Barros, R. & Gavrilyuk, S.L. 2007 Dispersive nonlinear waves in two-layer flows with free surface. II. Large amplitude solitary waves embedded into the continuous spectrum. Stud. Appl. Maths 119, 213–251.CrossRefGoogle Scholar
Benjamin, T.B. & Bridges, T.J. 1997 Reappraisal of the Kelvin–Helmholtz problem. Part 1. Hamiltonian structure. J. Fluid Mech. 333, 301–325.CrossRefGoogle Scholar
Camassa, R., Choi, W., Michallet, H., Rusas, P.O. & Sveen, J.K. 2006 On the realm of validity of strongly nonlinear asymptotic approximations for internal waves. J. Fluid Mech. 549, 1–23.CrossRefGoogle Scholar
Choi, W. 2000 Modeling of strongly nonlinear internal waves in a multilayer system. In Proceedings of the Fourth International Conference on Hydrodynamics (ed. Y. Goda, M. Ikehata & K. Suzuki), pp. 453–458. ICHD2000.Google Scholar
Choi, W. 2019 On Rayleigh expansion for nonlinear long water waves. J. Hydrodyn. 31, 1115–1126.CrossRefGoogle Scholar
Choi, W. 2022 High-order strongly nonlinear long wave approximation and solitary wave solution. J. Fluid Mech. 945, A15.CrossRefGoogle Scholar
Choi, W., Barros, R. & Jo, T.-C. 2009 A regularized model for strongly nonlinear internal solitary waves. J. Fluid Mech. 629, 73–85.CrossRefGoogle Scholar
Choi, W. & Camassa, R. 1996 Weakly nonlinear internal waves in a two-fluid system. J. Fluid Mech. 313, 83–103.CrossRefGoogle Scholar
Choi, W. & Camassa, R. 1999 Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396, 1–36.CrossRefGoogle Scholar
Choi, W., Goullet, A. & Jo, T.-C. 2011 An iterative method to solve a regularized model for strongly nonlinear long internal waves. J. Comp. Phys. 230, 2021–2030.CrossRefGoogle Scholar
Choi, W., Zhi, C. & Barros, R. 2020 High-order unidirectional model with adjusted coefficients for large-amplitude long internal waves. Ocean Model. 151, 101643.CrossRefGoogle Scholar
Debsarma, S., Das, K.P. & Kirby, J.T. 2010 Fully nonlinear higher-order model equations for long internal waves in a two-fluid system. J. Fluid Mech. 654, 281–303.CrossRefGoogle Scholar
Helfrich, K.R. & Melville, W.K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.CrossRefGoogle Scholar
Jo, T.-C. & Choi, W. 2002 Dynamics of strongly nonlinear solitary waves in shallow water. Stud. Appl. Math. 109, 205–228.CrossRefGoogle Scholar
Jo, T.-C. & Choi, W. 2008 On stabilizing the strongly nonlinear internal wave model. Stud. Appl. Math. 120, 65–85.CrossRefGoogle Scholar
Kodaira, T., Waseda, T., Miyata, M. & Choi, W. 2016 Internal solitary waves in a two-fluid system with a free surface. J. Fluid Mech. 804, 201–223.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Dover Publications.Google Scholar
Madsen, P.A., Bingham, H.B. & Liu, H. 2002 A new approach to high-order Boussinesq models. J. Fluid Mech. 462, 1–30.CrossRefGoogle Scholar
Miyata, M. 1988 Long internal waves of large amplitude. In Proceedings of the IUTAM Symposium on Nonlinear Water Waves (ed. H. Horikawa & H. Maruo), pp. 399–406. Springer Verlag.CrossRefGoogle Scholar
Rayleigh, L. 1876 On waves. Phil. Mag. Ser. (5) 1, 257–279.Google Scholar
Taklo, T.M.A. & Choi, W. 2020 Group resonant interactions between surface and internal gravity waves in a two-layer system. J. Fluid Mech. 892, A14.CrossRefGoogle Scholar
Wu, T.Y. 1999 Modeling nonlinear dispersive water waves. J. Eng. Mech. 11, 747–755.Google Scholar
Wu, T.Y. 2001 A unified theory for modeling water waves. Adv. Appl. Mech. 37, 1–88.CrossRefGoogle Scholar
de Zárate, A.R., Vigo, D., Nachbin, A. & Choi, W. 2009 A higher-order internal wave model accounting for large bathymetric variations. Stud. Appl. Math. 122, 275–294.CrossRefGoogle Scholar
Zhao, B.B., Ertekin, R.C., Duan, W.Y. & Webster, W.C. 2016 New internal-wave model in a two-layer fluid. J. Waterway, Port, Coastal, Ocean Engng 142, 04015022.CrossRefGoogle Scholar
Zhao, B.B., Wang, Z., Duan, W.Y., Ertekin, R.C., Hayatdavoodi, M. & Zhang, T. 2020 Experimental and numerical studies on internal solitary waves with a free surface. J. Fluid Mech. 899, A17.CrossRefGoogle Scholar