Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-31T14:44:41.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing and reaction in turbulent plumes: the limits of slow and instantaneous chemical kinetics

Published online by Cambridge University Press:  18 December 2018

N. Mingotti Open the ORCID record for N. Mingotti [Opens in a new window]  and
S. S. S. Cardoso
N. Mingotti*
Affiliation:
Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge CB3 0AS, UK
S. S. S. Cardoso
Affiliation:
Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge CB3 0AS, UK
*
†Email address for correspondence: nm441@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the behaviour of a reactive plume in the two limiting cases of slow and instantaneous chemical reactions. New laboratory measurements show that, whereas the slow reaction between the source and entrained chemical species takes place within the whole volume of each eddy in the plume, the fast reaction develops preferentially at the periphery of the eddies. We develop a new model that quantifies the mixing of the reactive buoyant fluids at the Batchelor scale and thereby the progress of the fast reaction. We present a series of new experimental results that suggest that a critical distance from the source, 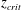$z_{crit}$, exists at which the volume of fluid that is entrained from the ambient is equal to that which is mixed within the plume at the Batchelor scale. For 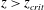$z>z_{crit}$, only a fraction of the entrained fluid is rapidly mixed and reacts with the plume fluid. The results of the new experiments enable us to quantify the distance from the source at which an instantaneous reaction reaches completion, and show that it can be significantly larger than the distance 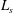$L_{s}$ at which the stoichiometric dilution of the plume fluid is achieved. In the limit of an instantaneous reaction, the longitudinal profiles of source chemical concentration in the plume depend on $(z_{crit}/L_{s})^{5/6}$. The predictions of the model are validated against the experimental results, and the profiles of source chemical concentration in the plume for slow and fast reactions are compared.

JFM classification

Mixing: Mixing Convection: Plumes/thermals Reacting Flows: Reacting Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 1 - 28
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allgayer, D. M. & Hunt, G. R. 2012 On the application of the light-attenuation technique as a tool for non-intrusive buoyancy measurements. Exp. Therm. Fluid Sci. 38, 257–261.Google Scholar
Atkins, P. W. 1978 Physical Chemistry. Oxford University Press.Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5, 113–133.Google Scholar
Bower, D. J., Caulfield, C. P., Fitzgerald, S. D. & Woods, A. W. 2008 Transient ventilation dynamics following a change in strength of a point source of heat. J. Fluid Mech. 614, 15–37.Google Scholar
Campbell, A. N. & Cardoso, S. S. 2010 Turbulent plumes with internal generation of buoyancy by chemical reaction. J. Fluid Mech. 655, 122–151.Google Scholar
Cardoso, S. S. & McHugh, S. T. 2010 Turbulent plumes with heterogeneous chemical reaction on the surface of small buoyant droplets. J. Fluid Mech. 642, 49–77.Google Scholar
Caulfield, C. P. & Woods, A. W. 1995 Plumes with non-monotonic mixing behaviour. Geophys. Astrophys. Fluid Dyn. 79, 173–199.Google Scholar
Conroy, D. T. & Llewellyn Smith, S. G. 2008 Endothermic and exothermic chemically reacting plumes. J. Fluid Mech. 612, 291–310.Google Scholar
Domingos, M. G. & Cardoso, S. S. 2013 Turbulent two-phase plumes with bubble-size reduction owing to dissolution or chemical reaction. J. Fluid Mech. 716, 120–136.Google Scholar
Domingos, M. G. & Cardoso, S. S. 2015 Turbulent thermals with chemical reaction. J. Fluid Mech. 784, 5–29.Google Scholar
Fox, R. O. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.Google Scholar
George, W. K., Alpert, R. L. & Tamanini, F. 1977 Turbulence measurements in an axisymmetric buoyant plume. Intl J. Heat Mass Transfer 20, 1145–1154.Google Scholar
Housecroft, C. E. & Constable, E. C. 2002 Chemistry, Equilibria. Prentice Hall.Google Scholar
Hunt, G. R. & van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Maths 76, 424–448.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Komori, S. & Ueda, H. 1984 Turbulent effects on the chemical reaction for a jet in a nonturbulent stream and for a plume in a grid-generated turbulence. Phys. Fluids 27, 77–86.Google Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2015 Fluid Mechanics. Academic Press.Google Scholar
Leaist, D. G. 1988 The effects of aggregation, counterion binding, and added NaCl on diffusion of aqueous methylene blue. Can. J. Chem. 66 (9), 2452–2457.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emtying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Lupton, J. E., Delaney, J. R., Johnson, H. P. & Tivey, M. K. 1985 Entrainment and vertical transport of deep-ocean water by buoyant hydrothermal plumes. Nature 316, 621–623.Google Scholar
Mingotti, N. & Woods, A. W. 2015a On the transport of heavy particles through a downward displacement-ventilated space. J. Fluid Mech. 774, 192–223.Google Scholar
Mingotti, N. & Woods, A. W. 2015b On the transport of heavy particles through an upward displacement-ventilated space. J. Fluid Mech. 772, 478–507.Google Scholar
Mingotti, N. & Woods, A. W. 2016 On turbulent particle fountains. J. Fluid Mech. 793, R1.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Mowry, S. & Ogren, P. J. 1999 Kinetics of methylene blue reduction by ascorbic acid. J. Chem. Educ. 76, 970–973.Google Scholar
Noulty, R. A. & Leaist, D. G. 1984 Activity coefficients and diffusion coefficients of dilute aqueous solutions of lithium, sodium, and potassium hydroxides. J. Solut. Chem. 13, 767–778.Google Scholar
Papanicolau, P. N. & List, E. J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195, 341–391.Google Scholar
Perry, R. H. & Green, D. W. 2008 Perry’s Chemical Engineers’ Handbook, 8th edn. McGraw-Hill.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Shamim, M. & Baki, S. M. A. 1980 Diffusion measurements in aqueous L-ascorbic acid solutions. Aust. J. Chem. 33, 1857–1861.Google Scholar
Snehalatha, T., Rajanna, K. C. & Saiprakash, P. K. 1997 Methylene blue – ascorbic acid, an undergraduate experiment in kinetics. J. Chem. Educ. 74, 228–233.Google Scholar
Someya, S., Yoshida, S., Tabata, T. & Okamoto, K. 2009 The effect of chemical reaction on the mixing flow between aqueous solutions of acetic acid and ammonia. Intl J. Heat Mass Transfer 52, 4236–4243.Google Scholar
Sparks, R. S. J., Bursik, M. I., Carey, S. N., Gilbert, J. S., Glaze, L. S., Sigurdsson, H. & Woods, A. W. 1997 Volcanic Plumes. Wiley.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Ulpre, H., Eames, I. & Greig, A. 2013 Turbulent acidic jets and plumes injected into an alkaline environment. J. Fluid Mech. 734, 253–274.Google Scholar
Vitagliano, V. & Lyons, P. A. 1956 Diffusion in aqueous acetic acid solutions. J. Am. Chem. Soc. 78 (18), 4538–4542.Google Scholar
Wittke, G. 1983 Reactions of phenolphthalein at various pH values. J. Chem. Educ. 60, 239–240.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Woods, A. W. & Caulfield, C. P. 1992 A laboratory study of explosive volcanic eruptions. J. Geophys. Res. 97, 6699–6712.Google Scholar
Yeh, H. & Wills, G. B. 1971 Diffusion coefficient of aqueous nitric acid at 25°C as function of concentration from 0.1 to 1.0 M. J. Chem. Engng Data 16, 76–77.Google Scholar