Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-03T17:58:15.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Type classification of extreme quantized characters

Part of: Linear algebraic groups and related topics Linear spaces and algebras of operators Ergodic theory

Published online by Cambridge University Press:  06 September 2019

RYOSUKE SATO
RYOSUKE SATO*
Affiliation:
Graduate School of Mathematics, Nagoya University, Chikusaku, Nagoya464-8602, Japan email d19001r@math.nagoya-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of quantized characters was introduced in our previous paper as a natural quantization of characters in the context of asymptotic representation theory for quantum groups. As in the case of ordinary groups, the representation associated with any extreme quantized character generates a von Neumann factor. From the viewpoint of operator algebras (and measurable dynamical systems), it is natural to ask what is the Murray–von Neumann–Connes type of the resulting factor. In this paper, we give a complete solution to this question when the inductive system is of quantum unitary groups 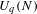$U_{q}(N)$.

Keywords

operator algebrasclassical ergodic theoryasymptotic representation theoryquantum groupsorbit equivalence relations

MSC classification

Primary: 20G42: Quantum groups (quantized function algebras) and their representations 47L55: Representations of (nonselfadjoint) operator algebras 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 593 - 605
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyer, R. P.. Infinite traces of AF-algebras and characters of U (∞). J. Operator Theory 9 (1983), 205–236.Google Scholar
Brown, G., Dooley, A. H. and Lake, J.. On the Krieger–Araki–Woods ratio set. Tôhoku Math. J. 47 (1995), 1–13.10.2748/tmj/1178225632CrossRefGoogle Scholar
Cuenca, C.. Asymptotic formulas for Macdonald polynomials and the boundary of the (q, t)-Gelfand–Tsetlin graph. SIGMA 14 (2018), No. 001, 66 pp.Google Scholar
Durrett, R.. Probability: Theory and Examples (Cambridge Series in Statistical and Probabilistic Mathematics, 31) , 4th edn. Cambridge University Press, Cambridge, 2010.10.1017/CBO9780511779398CrossRefGoogle Scholar
Gorin, V.. The q-Gelfand–Tsetlin graph, Gibbs measures and q-Toeplitz matrices. Adv. Math. 229(1) (2012), 201–266.10.1016/j.aim.2011.08.016CrossRefGoogle Scholar
Kosloff, Z.. On a type III1 type Bernoulli shift. Ergod. Th. & Dynam. Sys. 31(6) (2011), 1727–1747.10.1017/S0143385710000647CrossRefGoogle Scholar
Neshveyev, S. and Tuset, L.. Compact Quantum Groups and Their Representation Categories. Société Mathématique de France, Paris, 2013.Google Scholar
Noumi, M., Yamada, H. and Mimachi, K.. Finite dimensional representations of the quantum group GLq(n; ℂ) and the zonal spherical functions on U q(n - 1)\U q(n). Jpn. J. Math. 19(1) (1993), 31–80.10.4099/math1924.19.31CrossRefGoogle Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem (Lecture Notes in Mathematics, 1757) , 2nd edn. Springer, Berlin, 2001.10.1007/b76887CrossRefGoogle Scholar
Sato, R.. Quantized Vershik–Kerov theory and quantized central probability measures on branching graphs. J. Funct. Anal. 277 (2019), 2522–2557.10.1016/j.jfa.2018.11.016CrossRefGoogle Scholar
Takesaki, M.. Theory of Operator Algebras I, II, III (Encyclopedia of Mathematical Sciences, 127) . Springer, Berlin, 2003.Google Scholar
Tomatsu, R.. A characterization of right coideals of quotient type and its application to classification of Poisson boundaries. Commun. Math. Phys. 275 (2007), 271–296.10.1007/s00220-007-0267-6CrossRefGoogle Scholar
Vershik, A. M. and Kerov, S. V.. Characters and factor representations of the infinite unitary group. Dokl. Akad. Nauk. SSSR 267(2) (1982), 272–276.Google Scholar
Voiculescu, D.. Représentations factorielles de type II de U (∞). J. Math. Pures Appl. (9) 55 (1976), 1–20.Google Scholar
Yoshida, M.. Odometer action on Riesz product. J. Aust. Math. Soc. (Series A) 61 (1996), 141–149.Google Scholar
Z̆elobenko, D. P.. Compact Lie Groups and their Representations (Translations of Mathematical Monographs, 40) . American Mathematical Society, Providence, RI, 1973.10.1090/mmono/040CrossRefGoogle Scholar