The exact Hausdorff measure of the sample path for planar Brownian motion
Published online by Cambridge University Press: 24 October 2008
Extract
It has long been known (see Lévy (3), pp. 256, 260) that the sample paths of Brownian motion in the plane form an everywhere dense set of zero Lebesgue measure, with probability 1. In (7), a capacity argument was used to show that the Hausdorff measure with respect to tα is infinite for 0 < α < 2 with probability 1 so that the dimension of the path set is known to be 2. If one considers the initial part of the sample path Cω = C(1, ω) for 0 ≤ t ≤ 1, then it becomes interesting to ask if there is a measure function ψ(t) such that, with probability 1,

for suitable positive constants c1, c2. The corresponding problem for paths in k-space (k ≥ 3) has been solved. In this case, if φ1(t) = t2 log log t−1, Lévy (4) obtained the upper bound and Ciesielski and Taylor (1) obtained the lower bound. For the planar case, the path is recurrent, and the intricate fine structure makes the measure function φ1(t) inappropriate. In (2), Erdő and Taylor showed that the measure is finite with probability 1 with respect to φ2(t) = t2 log t−1, and at that time we thought that (1) might be true with ψ(t) = φ2(t). Recently Ray (5) has obtained the lower bound in (1)with
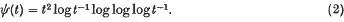
The purpose of the present note is to obtain the upper bound in (1) for the same measure function, thus showing that (2) defines the correct measure function for measuring planar Brownian motion.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 2 , April 1964 , pp. 253 - 258
- Copyright
- Copyright © Cambridge Philosophical Society 1964
References
REFERENCES
- 32
- Cited by




