Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-29T19:01:08.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetries in the fourth Painlevé equation and Okamoto polynomials

Published online by Cambridge University Press:  22 January 2016

Masatoshi Noumi  and
Yasuhiko Yamada
Masatoshi Noumi
Affiliation:
Department of Mathematics, Kobe University Rokko, Kobe 657-8501, Japan, noumi@math.kobe-u.ac.jp
Yasuhiko Yamada
Affiliation:
Department of Mathematics, Kobe University Rokko, Kobe 657-8501, Japan, yamaday@math.kobe-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

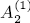The fourth Painlevé equation PIV is known to have symmetry of the affine Weyl group of type with respect to the Bäcklund transformations. We introduce a new representation of PIV, called the symmetric form, by taking the three fundamental invariant divisors as the dependent variables. A complete description of the symmetry of PIV is given in terms of this representation. Through the symmetric form, it turns out that PIV is obtained as a similarity reduction of the 3-reduced modified KP hierarchy. It is proved in particular that the special polynomials for rational solutions PIV, called Okamoto polynomials, are expressible in terms of the 3-reduced Schur functions.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 153 , 1999 , pp. 53 - 86
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1999

References

[1] Fukutani, S., Okamoto, K. and Umemura, H., Special polynomials associated with the rational solutions and the Hirota bilinear relations of the 2nd and the 4th Painlevé equations, preprint.Google Scholar
[2] Jimbo, M. and Miwa, T., Solitons and infinite dimensional Lie algebras, Publ. RIMS, Kyoto Univ., 19 (1983), 943–1001.CrossRefGoogle Scholar
[3] Kac, M. and van Moerbeke, P., On an explicitly soluble system of nonlinear differential equations related to certain Toda lattices, Advances Math., 16 (1975), 160–169.CrossRefGoogle Scholar
[4] Murata, Y., Rational solutions of the second and the fourth equations of Painlevé, Funkcialaj Ekvacioj, 28 (1985), 1–32.Google Scholar
[5] Nishitani, T. and Tajiri, M., On similarity solutions of Boussinesq equation, Phys. Lett., 89A (1982), 379–380.CrossRefGoogle Scholar
[6] Noumi, M. and Okamoto, K., Irreducibility of the second and the fourth Painlevé equations, Funkcialaj Ekvacioj, 40 (1997), 139–163.Google Scholar
[7] Okamoto, K., Studies on Painlevé equations III, Second and fourth Painlevé equations PII and PIV , Math. Ann., 275 (1986), 221–255.CrossRefGoogle Scholar
[8] Okamoto, K., Algebraic relations among six adjacent τ-functions related to the fourth Painlevé system, Kyushu J. Math., 50 (1996), 513–532.CrossRefGoogle Scholar
[9] Umemura, H., On the irreducibility of the first differential equations of Painlevé.CrossRefGoogle Scholar
[10] Quispel, G. R. W., Nijhoff, F.W. and Capel, H. W., Linearization of the Boussinesqequation and the modified Boussinesq equation, Phys. Lett., 91A (1982), 143–145.CrossRefGoogle Scholar