1 Introduction

Precise three-dimensional (3D) localization is essential for a variety of advanced microscopy techniques, including defect-based sensing [1, 2], multiplane detection [3, 4], single-particle tracking [5–7]. Especially, as the position of individual fluorophores can be determined with a precision smaller than the size of the point spread function (PSF), a super-resolution image can be assembled from the estimated positions of the sufficient fluorescent labels [8–11], to avoid the Abbe–Rayleigh criterion [12, 13]. The effective achievable resolution is closely related to the precision of individual fluorophore localization. The 3D localization is intimately connected to multi-parameter estimation. Therefore, the advantages of these techniques are better understood in the multi-parameter framework.

Building upon the pioneering work of Tsang and coworkers in quantifying far-field two-point super-resolution [14–16], the ultimate precision limits of single point source’s localization have been extensively investigated [17–19]. The basic idea is to exploit the quantum Fisher information (QFI) and associated quantum Cramér-Rao bound (QCRB) [20, 21]. Its theory proves to be effective in establishing under which conditions systems may be preferable to estimate parameters. Common imaging strategies rely on complicated experimental setups to achieve the quantum-mechanical bound, such as interferometer arrangement [22, 23], mode sorter [24, 25], and spatial-mode demultiplexing (SPADE). The multi-parameter cases often involve trade-off relations among the uncertainties on the parameter, since the total information has now to be apportioned [26, 27]. This makes the multi-parameter optimization problem more involved and more intriguing.

Given the close relationship between QFI and the characteristics of the light field, precision can be significantly enhanced by modifying the system’s response, such as through PSF engineering [28–30]. Recent studies have demonstrated the immense potential of LG modes, as opposed to conventional Gaussian mode, for improving 3D localization precision [31]. The superposition of LG modes, specifically the rotation mode characterized by their intensity profiles that rotate on propagation, further enhances the ultimate precision of axial localization. Moreover, the ultimate axial precision of LG modes can be achieved with intensity detection [32, 33]. The simplicity and feasibility of intensity detection make it extremely valuable for microscopy applications, circumventing potential systematic errors and losses inherent in complex strategies delineated previously [34]. However, practical intensity detection introduces pixelated readouts and inherent detection noise, which can compromise the theoretical advantages offered by this simple optimal strategy. Therefore, rigorous mathematical analysis and robust localization algorithms are necessary.

In this work, we rigorously derive the ultimate 3D localization limits of LG modes and rotation modes in the multi-parameter estimation framework. We investigate the accessibility of these limits under ideal intensity detection conditions. Furthermore, we consider the practical limitations imposed by finite pixel size and various detector noise sources. Taking these factors into account, we develop a robust maximum likelihood estimation (MLE) algorithm that iteratively determines the 3D position of a point source. Our algorithm robustly achieves the CRB under low signal-to-noise ratio (SNR) and aberrational conditions. Moreover, it is not limited to symmetric PSFs, but can be extended to accommodate anisotropic PSFs, as well as diverse noise statistics. In this manner, we present comprehensive theoretical and experimental evidence aiming at exhibiting remarkable super-localization capabilities facilitated by LG and rotation modes.

2 Theoretical framework

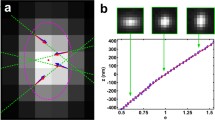
Localization can be regarded as a multi-parameter estimation problem, aiming to determine the 3D coordinates of a point source in the image space, as depicted in Fig. 1(a). Assuming an initial state denoted by \(\vert \Psi _{(0)}\rangle \) in the image space, the 3D displacement can be described by a unitary operation:

$$\begin{aligned} \vert \tilde{\Psi}_{(x_{e},y_{e},z_{e})}\rangle =\exp (-i \hat{G}_{z} z_{e}-i \hat{p}_{x} x_{e}-i \hat{p}_{y} y_{e})\vert \Psi _{(0)}\rangle. \end{aligned}$$
(1)

Here, the operators \(\hat{p}_{x}=-i\partial _{x}\) and \(\hat{p}_{y}=-i\partial _{y}\) represent the lateral displacement as momentum operators, and the axial displace operator is denoted as \(\hat{G}_{z}=-i\partial _{z}=\frac{1}{2 k} \nabla _{T}^{2}+k\), where k is the wavenumber and \(\nabla _{T}^{2}=\partial _{x x}+\partial _{y y}\). These operators commute with each other, enabling simultaneous measurement of these unknown parameters [35, 36]. Through the aforementioned approach, the state in the image space, represented by \(\rho _{\theta}=\vert \tilde{\Psi}\rangle \langle \tilde{\Psi}\vert \), is parameterized with point source 3D coordinates \(\theta =(x_{e},y_{e},z_{e})\). The image is a magnified replica of the state \(\vert \Psi _{(x',y',z')}\rangle \) in the object space [37]. The estimation of 3D coordinates of the object requires a parametric transformation related to the magnification factor of the system.

Figure 1
figure 1

(a) Schematic illustration of the 3D localization of a point source with an optical microscope-based imaging setup. (b) Schematic illustration of the lateral intensity profiles variation with the rotation mode at different axial positions

Full size image

To proceed further, we consider a shifted normalized LG mode, with a transverse field in the detection plane, given by [38]

$$\begin{aligned} \begin{aligned} &LG_{lp}(r,\phi,z)\\ &\quad=\langle x,y,z\vert \tilde{\Psi}_{(x_{e},y_{e},z_{e})} \rangle \\ &\quad=\sqrt{\frac{2 p !}{\pi (p+ \vert l \vert ) !}} \\ &\qquad{}\times \frac{1}{w(z)} \biggl[\frac{\sqrt{2r^{2}}}{w(z)} \biggr]^{ \vert l \vert }L_{p}^{ \vert l \vert } \biggl[\frac{2 r^{2}}{w(z)^{2}} \biggr] \exp \biggl[-\frac{r^{2}}{w (z )^{2}} \biggr] \\ &\qquad{}\times \exp \biggl[-i \biggl(k z-\frac{kr^{2}}{2 R(z)}+ \vert l \vert \phi + \zeta _{lp}(z) \biggr) \biggr], \end{aligned} \end{aligned}$$
(2)

where \(r^{2}=(x-x_{e})^{2}+(y-y_{e})^{2}\), \(\phi =(x-x_{e})/(y-y_{e})\), \(L_{p}^{\vert l \vert} [\cdots ]\) is the generalized Laguerre polynomial defined by azimuthal index \(l\in \mathbb{Z}\) and radial index \(p \in \mathbb{Z}^{+}\). The transverse field distribution is determined by the beam waist radius \(w_{0}\) and the Rayleigh range \(z_{R}\) through \(R(z)=(z-z_{e}) [1+( \frac{z_{\mathrm{R}}}{z-z_{e}})^{2} ]\), \(w^{2}(z)=w_{0}^{2} [1+(\frac{z-z_{e}}{z_{\mathrm{R}}})^{2} ]\), \(\zeta _{lp}(z)=(2 p+\vert l\vert +1) \arctan ( \frac{z-z_{e}}{z_{\mathrm{R}}})\) and \(z_{R}=\frac{\pi w_{0}^{2}}{\lambda}\). To streamline the derivation, we redefine the coordinate system with the detection plane serving as the origin, denoted as \(z=0\) and \(z_{e}\) represents the distance between the detection plane and the focal plane.

The 3D localization precision is quantified by the covariance matrix \(\operatorname{Cov}(\boldsymbol{\Pi}, \tilde{\theta})\) of locally unbiased estimators, which is lower bounded by Cramér-Rao bound (CRB) and QCRB:

$$\begin{aligned} \operatorname{Cov}(\boldsymbol{\Pi}, \tilde{\theta}) \ge \frac{1}{N} \mathcal{F} (\rho _{\theta}, \boldsymbol{\Pi} )^{-1}\ge \frac{1}{N} \mathcal{Q} (\rho _{\theta} )^{-1}, \end{aligned}$$
(3)

where N is the number of system copies related to the effective photon counts in each frame. The associated classical Fisher information matrix (CFIm), denoted as \(\mathcal{F} (\rho _{\theta}, \boldsymbol{\Pi} )\) is defined by

$$\begin{aligned} \mathcal{F}_{ij} (\rho _{\theta}, \boldsymbol{\Pi} )=\sum_{X_{k}} \frac{1}{P (X_{k} \vert \theta )} \frac{\partial P (X_{k} \vert \theta )}{\partial \theta _{i}} \frac{\partial P (X_{k} \vert \theta )}{\partial \theta _{j}}, \end{aligned}$$
(4)

where \(P (X_{k} \vert \theta )\) is the conditional probability density of observing an outcome \(X_{k}\) depending on the underlying 3D position θ of the source, and a specific measurement Π. The associated QFI matrix (QFIm), denoted as \(\mathcal{Q}(\rho _{\theta})\), gives the maximum of the CFIm. In the case of pure states, as is the situation we consider, the QFIm is four times the covariance matrix of the generators, which consists solely of diagonal entries.

The axial QFI for arbitrary LG modes has been recently worked out in Ref. [33], we extend the results into a 3D scenario, which can be expressed as:

$$\begin{aligned} \begin{aligned} & \mathcal{Q}_{x,y}=\frac{4(2p+ \vert l \vert +1)}{w_{0}^{2}},\\ & \mathcal{Q}_{z}= \frac{2p(p+ \vert l \vert )+2p+ \vert l \vert +1}{z_{R}^{2}}. \end{aligned} \end{aligned}$$
(5)

The lateral QFI exhibits a linear dependence on p, while the axial QFI shows a quadratic dependence on p, highlighting the significant role of the radial index in effectively enhancing 3D localization precision. These findings are consistent with the numerical results presented in Ref. [31] for low-order LG modes. Notably, the \(LG_{00}\) mode is the Gaussian mode, serving as a classical benchmark for comparative analysis.

While LG modes exhibit trivial divergence during propagation, more intricate intensity transformations can be achieved by superposing different LG modes. In particular, when employing a set of M constituent LG modes that satisfy the relation \([(2p+l)_{j+1}-(2p+l)_{j}]/[l_{j+1}-l_{j}]\equiv const \equiv V\) for \(j=1,2,\ldots, M-1\), the resulting intensity pattern exhibits anisotropy (with non-circular symmetry) and undergoes rotation during the propagation [39, 40]. As illustrated in Fig. 1(b), the overall rotation angle from the waist to the far field is given by \(\Delta \phi (z_{e}=\infty )=V\pi /2\), and \(\Delta \phi (z_{e}=-\infty )=-V\pi /2\). Notably, half of Δϕ is obtained at the Rayleigh range. These PSFs offer a wider range of applications in super-resolution imaging due to their superior localization precision compared to circular symmetric PSFs [11, 41, 42]. To provide a clear physical intuition, we consider the simple example of the superposition of two LG modes (M=2) with \(l\neq l^{\prime}\) and \(p=p^{\prime}=0\). The 3D QFI for rotation modes can be determined as follows:

$$\begin{aligned} \begin{aligned} &\mathcal{Q}_{x,y}= \frac{2( \vert l \vert + \vert l^{\prime} \vert +2)}{w_{0}^{2}}, \\ &\mathcal{Q}_{z}=\frac{[4+2( \vert l \vert + \vert l' \vert )+( \vert l \vert - \vert l' \vert )^{2}]}{z_{R}^{2}}. \end{aligned} \end{aligned}$$
(6)

In contrast to the quadratic precision improvement in the axial localization, the lateral QFI is obtained by summing up the contributions from individual modes.

Typically, the QFI is distributed between the phase and intensity variations of the measured beam. Remarkably, by discarding the phase information, the full axial QFI can still be extracted [33]. This result prompts us to investigate the efficacy of intensity detection in achieving ultimate 3D localization precision. When ideal detection conditions are assumed, i.e. a detector of infinite area without pixelation and no additional noise sources except for shot noise, the intensity detection projects the quantum state onto the eigenstates of spatial coordinates, represented as \(\boldsymbol{\Pi}_{x, y}=\vert x, y\rangle \langle x, y\vert \). In consequence, the probability density is \(P(X_{k}\vert \theta )=\operatorname{Tr} (\rho _{\theta } \boldsymbol{\Pi}_{x, y})=\vert \tilde{\Psi}_{(x_{e},y_{e},z_{e})} \vert ^{2}\), which corresponds to the (normalized) beam intensity \(\vert LG_{lp}\vert ^{2}\). The summation in Eq. (4) transforms into a two-dimensional integral over the spatial domain. For LG modes, after a lengthy calculation, the ideal CFI can be expressed analytically as follows:

$$\begin{aligned} \begin{aligned} &\mathcal{F}_{x,y}(z_{e})=\frac{4(2p+1)}{{w(z_{e})}^{2}},\\ & \mathcal{F}_{z}(z_{e})= \frac{4[2p(p+ \vert l \vert )+2p+ \vert l \vert +1]}{{R(z_{e})}^{2}}. \end{aligned} \end{aligned}$$
(7)

These results are plotted in Fig. 2. Two detection planes can be found, where full axial QFI and a portion of lateral QFI can be extracted. In the case of certain LG modes with \(\vert l \vert =0\), the lateral CFI can reach the QFI at the beam waist, \(\mathcal{F}_{x,y}(0)=\mathcal{Q}_{x,y}\), while the axial CFI can reach it at the Rayleigh range, \(\mathcal{F}_{z}(\pm z_{R})=\mathcal{Q}_{z}\). Intuitively, the precision of axial localization depends on the beam divergence, which determines the rate of beam width variations during propagation. The precision of lateral localization benefits from sharpness of the wave packet. By increasing the radial index p, the sharpness and the beam divergence are enhanced [43], leading to an improvement in the precision of 3D localization. However, as the azimuthal index l is increased, a central dark spot emerges and expands in size. Although this leads to increased divergence, it fails to enhance the sharpness of the beam, thereby hindering improvements in the precision of lateral localization. In the case of rotation modes, we consider the superposition of \(LG_{00}\) and \(LG_{20}\) modes as a representative example. Numerical analysis suggests that only a small fraction of the 3D QFI can be extracted with intensity detection. As this specific category lacks radial information, the average lateral CFI is equivalent to that of the \(LG_{00}\), see Fig. 2(a). However, the non-stationary rotation behavior significantly enhances axial CFI in the near-focus axial region compared to single LG mode, as shown in Fig. 2(b). These results also underscore the significance of developing quantum-inspired strategies, such as SPADE or mode sorting techniques, to reveal all information about the parameter. Comprehensive derivations of the QFIm and ideal CFIm are included in the Additional file 1.

Figure 2
figure 2

The (a) lateral CFI and (b) axial CFI for ideal intensity detection as a function of the distance between detection plane and the focal plane. The average lateral CFI of the rotation mode is equivalent to that of \(LG_{00}\). The horizontal dashed lines indicate the QFI of each mode. Each curve is normalized to the QFI of \(LG_{00}\)

Full size image

We then incorporate the deteriorating effects in the detection process and present our MLE algorithm. Previous studies have demonstrated that the localization algorithms based on MLE can asymptotically approach the CRB for a few specific scenarios [44–46], outperforming nonlinear least squares (NLLS) algorithm [47]. However, discrepancies between the variances of MLE and the precision predicted by the CRB have been observed in the presence of model mismatches and misspecifications [25, 46], such as inaccurate noise statistics, PSF mismatch, optical aberrations, and low SNR. These limitations stem from the fact that existing localization MLE algorithms make simplified statistical assumptions for specific scenarios, which inspires us to improve the robustness and generalisability of MLE algorithms by adopting a more refined statistical model. In the case of pixelated intensity detection, the measurements can be described as \(\boldsymbol{\Pi}_{A_{k}} = \int _{A_{k}} \vert x, y\rangle \langle x, y\vert \,dx\,dy \). The readout counts in the kth pixel encompass the integrated photon counts \(N_{k}\) and contributions from detector noise, which can be expressed as:

$$\begin{aligned} X_{k} = N \int _{A_{k}} \vert \tilde{\Psi}_{(x_{e},y_{e},z_{e})} \vert ^{2}\,dx\,dy + N_{b} + N_{c}. \end{aligned}$$
(8)

The photon-electric conversion process in the CCD camera distorts the effective photon counts, resulting in two types of detection noise. The term \(N_{b}\) represents signal-independent noise, including background fluorescence, dark current, and readout noise. On the other hand, the variance of \(N_{c}\) positively correlates with the signal and arises in the electron amplification process [48]. The SNR is determined by the ratio of the average effective photon counts to the noise present at each pixel. These statistical assumptions have been successfully applied in weak measurement scenarios with limited SNR and detector dynamic range [49, 50].

Based on the statistical model mentioned above, we describe the MLE algorithm to estimate the parameters with the likelihood function:

$$\begin{aligned} \mathrm{ln} \mathbf{L}(\vec{X}\vert \theta ) = \sum _{k} \mathrm{ln} P(X_{k} \vert \theta ). \end{aligned}$$
(9)

The estimated results, denoted as θ̂, maximize the likelihood function. We employ the scoring method to iteratively update the parameter estimates using the inverse of the CFIm and the derivative of the likelihood function:

$$\begin{aligned} \hat{\theta}_{n+1} = \hat{\theta}_{n} + \mathcal{F}(\rho _{\theta}, \boldsymbol{\Pi}_{A_{k}})^{-1} \frac{\partial \mathrm{ln} \mathbf{L}(\vec{X}\vert \theta )}{\partial \theta} \bigg\vert _{\theta =\hat{\theta}_{n}}. \end{aligned}$$
(10)

The iterative update scheme is similar to previous approaches in Refs. [46, 51], but improves iteration stability and reduces computational complexity [52].

For a system with unknown \(w_{0}\), the algorithm simultaneously estimates three unknown parameters: \(\theta =(x_{e},y_{e}, w(z_{e}))\). We assume the nominal axial distance is known, and the estimated beam width is used to determine the system’s \(w_{0}\) and \(z_{R}\). The lateral variance \(\operatorname{var}(\hat{x}_{e},\hat{y}_{e})\) can be directly calculated, while axial \(\operatorname{var}(\hat{z}_{e})\) can be derived using error propagation \(\operatorname{var}(\hat{z}_{e})=\operatorname{var}(\hat{w}(z_{e}))/[\partial _{z_{e}} \hat{w}(z_{e})]^{2}\). If the system is fully pre-calibrated with a known \(w_{0}\), the algorithm can estimate \(z_{e}\) instead of \(w(z_{e})\) with slight modification to handle anisotropic PSF, enabling direct 3D position estimation, as demonstrated in the following rotation mode experiment.

3 Experiment

3.1 Experiment setups

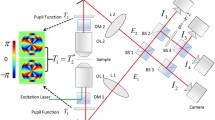
To validate our theoretical framework, we conducted experimental 3D localization using imperfect Gaussian mode, LG modes, and the rotation mode. The experimental setup is schematized in Fig. 3. In these experiments, we use the focus beam waist as a simplified point source realization.

Figure 3
figure 3

Experimental setups for 3D localization of a point source. The notations used are as follows: (N)PBS, (non) polarized beam splitter; BE, beam expander; SLM, spatial light modulator; AS, aperture stop; HWP, half-wave plate; BD, beam displacer; ICCD, intensified charge-coupled devices. A detailed description of the functions performed by modules (a)-(c) can be found in the text. (d) Measured intensity patterns with cross sections (asterisk) and corresponding fitted profiles (solid curves)

Full size image

We first assess the performance of the MLE algorithm in the presence of model mismatches and misspecifications by 3D localizing an imperfect Gaussian mode. A He–Ne laser at wavelength \(\lambda =633 \text{nm}\) serves as the Gaussian source. A single lens in Module (b) is utilized to form the image, which leads to a beam waist \(w_{0}=77.48\mu \text{m}\) and corresponding Rayleigh range \(z_{R}=29.8\text{mm}\). The spatially unfiltered laser and the spherical aberration of the image system lead to the imperfection of Gaussian mode [53]. A sequence of images is captured at different axial positions using a scientific ICCD camera (Andor, iStar CCD 05577H) with pixel size \(13\mu \text{m} \times 13\mu \text{m}\). The axial positions range over a span of 60mm with an interval of 3mm. At each position, we acquire 600 intensity images. The pre-calibration noise are characterized by \(N_{b}\sim \mathcal{N} (515.6, 7.1^{2} )\) and \(N_{c}\sim \mathcal{N} (0, \sigma _{c}^{2} )\). Here, \(\ln (\sigma _{c}^{2} )=1.4 \ln (N_{k} )-0.7\) and \(N_{k}\) represents the effective photon counts per pixel. It is worth noting that while Gaussian noise aligns with our CCD response calibration, other statistical distributions can also be accommodated in the algorithm. The effective photon counts per image are approximately \(N=1\times 10^{4}\), obtained by subtracting the detector noise from the total readout. These conditions reflect the typically low SNR encountered in real microscopy scenarios.

We then compare the 3D localization precision of LG modes and the rotation mode, demonstrating their super-localization capabilities. The desired PSFs are generated using a double-fourier transform optical setup, as depicted in Module (a). Computer-generated holograms (CGH) are imprinted onto the SLM (Meadowlark Optics, P1920-400-800-HDMI), with the desired first-order diffraction selected by a 4f system [54–56]. The waist radius of CGHs is uniformly set to \(500\mu \text{m}\). The second lens of the 4-f system is slightly displaced from the focal plane to ensure proper beam focusing. The modulation efficiency of the SLM is adjusted by an HWP. To mitigate the adverse impacts of beam jitter and turbulence, an additional HWP and a BD in Module (c) are employed to create two copies of the output beam, namely the left and right beams. These negative effects have less impact considering the previous single-lens imaging systems. By subtracting the estimation results obtained from two replicated beams, we obtain the final variance \(\operatorname{var}(\hat{\theta})=\operatorname{var}(\hat{\theta}_{\mathit{left}}-\hat{\theta}_{\mathit{right}})/2\). To ensure a fair comparison, the different modes are normalized to have the same effective photon counts. Each stack is comprised of 200 images. An overview of the measured (normalized) intensity patterns is summarized in Fig. 3(d). The model mismatch is characterized by the deviation from the ideal lateral intensity distribution and beam divergence, as discussed in detail in the Additional file 1. The results indicate that the imperfect Gaussian mode exhibits a severe model mismatch compared to modes generated through the 4f system.

The 3D localization precision is quantified by the covariance matrix. As the matrix contains only diagonal entries, the variance of each estimator is sufficient to measure the precision. To obtain error bars for the variances, we divide the raw data into 20 groups assuming repeated experiments.

3.2 Experiment results

The experimental results related to imperfect Gaussian mode are summarized in Fig. 4. Our algorithm is referred to as Model A. As a comparison, we employ another widely used localization MLE algorithm, referred to as Model B, as described in Ref. [46]. The key distinction between the two models lies in Model B’s consideration of a Poisson noise source \(N_{b}\) while neglecting the contribution of \(N_{c}\). Additionally, Model B treats N and \(N_{b}\) as unknown parameters, and offers direct estimation of \(\theta =(x_{e},y_{e},w(z_{e}),N,N_{b})\). As the sub-CFIm of \(\theta =(w(z_{e}), N, N_{b})\) contains non-diagonal entries, N and \(N_{b}\) can often be thought of nuisance parameters [57].

Figure 4
figure 4

Comparison between the 3D localization precision of imperfect Gaussian mode for (a) \(x_{e}\) (b) \(y_{e}\) and (c) \(z_{e}\) position using different MLE algorithms. The theoretical results (lines) are determined by the CRB and the experimental results (points) are obtained using MLE

Full size image

As illustrated in Fig. 4, the ultimate localization precision is given by the QCRB, while CRB of ideal intensity detection reaches QCRB at the focus and the Rayleigh range. The presence of noise diminishes the precision achievable with the ideal CRB. To address this issue, the practical CRB can be obtained using the statistical models, as discussed in detail in the Additional file 1. With increasing the distance between the detection plane and the focal plane, the SNR decreases, widening the gap between the practical CRB and the ideal one. By employing a more refined statistical model, Model A accurately predicts the CRB. Conversely, Model B provides a significantly non-tight CRB due to noise misspecification, specifically the Poisson assumption overestimating the variance of the noise. Both algorithms obtain similar precision in the lateral direction, see Fig. 4(a)-(b). However, as the distance increased, substantial discrepancies in the variance of axial localization become apparent, as shown in Fig. 4(c). We infer that these discrepancies may be attributed to nuisance parameters and model mismatch, which often result in reduced algorithm precision [47, 58]. The inaccurate estimation of \(w(z_{e})\) occurs due to the biased estimations of N and \(N_{b}\) when there exist PSF mismatches caused by aberrations (Fig. S2(a) (Additional file 1)). The limitation of Model B in achieving the axial CRB has also been observed in previous works [25, 46]. These results align with our intuition that a more refined model, taking into account more characteristics of the experimental apparatus, enhances the algorithm’s precision and robustness against model misspecification and mismatches.

The experimental results of 3D localizing a set of LG modes are presented in Fig. 5(a)-(c). The images are captured at \(10\mu \text{m}\) intervals within a \(100\mu \text{m}\) range, while the Rayleigh range is approximately \(52.71\mu \text{m}\). By ensuring modulation accuracy and efficiency, continual improvement in 3D localization precision can be achieved using higher-order modes. Specifically, for the highest-order mode \(LG_{12}\) generated in our experiment, the variance of the lateral localization is \(0.86\times 10^{-3} \text{mm}^{2}\) and the variance of the axial localization is \(0.25\times 10^{3} \text{mm}^{2}\). In comparison, the \(LG_{00}\) mode, which serves as the classical benchmark, achieves a lateral localization precision of \(2.03\times 10^{-3} \text{mm}^{2}\) and an axial localization precision of \(7.28\times 10^{3} \text{mm}^{2}\) under the same detection conditions. The results exhibit a enhancement of up to two-fold in lateral localization precision and up to twenty-fold in axial localization precision when employing LG modes. However, the deleterious effects of pixelation and noise will be exacerbated in higher-order modes (Fig. S4 (Additional file 1)). It is imperative to assess these potential limitations in order to achieve the anticipated precision improvement. Additionally, we present the results of the axial localization experiment for the rotation mode in Fig. 5(d), along with the constituent modes \(LG_{00}\) and \(LG_{20}\). Instead of changing the axial distance of the detector plane, a series of holograms are utilized to simulate the propagation of the light field. By performing a pre-calibration of the beam waist, our algorithm enables direct estimation of 3D coordinates. In the vicinity of the focal plane, the CFI of LG modes approaches zero, with their lateral intensity distributions seldom changing during propagation. Moreover, the likelihood function of LG modes exhibits the same values in two axial positions, leading to an ambiguous axial position estimate of ±z. In contrast, rotation modes exhibit a unique and easily detectable rotation angle \(\Delta \phi (z_{e})\) as they propagate [33, 39]. This characteristic eliminates the ambiguity of ±z and greatly improves the precision of axial localization. The experimental results highlight the exceptional precision in the axial localization achieved with the rotation mode in the near-focus region, surpassing that of the LG modes.

Figure 5
figure 5

Experimental results of LG modes and the rotation mode with the lateral localization precision of (a) \(LG_{l=0,p=\{0,1,2\}}\) modes and (b) \(LG_{l=1,p=\{0,1,2\}}\) modes as well as the axial localization precision of (c) \(LG_{l=\{0,1\},p=\{0,1,2\}}\) modes and (d) the rotation mode. The theoretical results (lines) are determined by the CRB and the experimental results (points) are obtained using MLE

Full size image

4 Conclusion

In summary, our research provides both theoretical and experimental evidence showcasing the exceptional potential of LG and rotation modes for 3D super-localization. To address practical challenges, we develop an iterative MLE algorithm that effectively estimates the 3D positions of point sources with the best possible precision determined by the CRB. By incorporating a refined noise statistic model, our algorithm improves the robustness and generalizability of the localization process, offering significant advantages in scenarios with low SNR and aberrations.

While higher-order or intricate superposition modes demonstrate theoretical advantages in ideal intensity detection, practical experimental imperfections pose challenges in realizing these benefits with PSF engineering and intensity-based strategies. Therefore, when exploring and optimizing the final effective resolution, the practical CRB provided by our algorithm can serve as a reliable benchmark for evaluating precision improvements. Our work builds a bridge between the quantum estimation framework and practical microscopy algorithm, fostering promising advancements in 3D super-resolution microscopy.