1 Introduction

The power Lindley (PL) distribution and two-parameter Lindley (TPL) distribution were introduced by [8] and [17] respectively, these distributions are an extension to a known Lindley distribution which was proposed by [14]. After two years [2] introduced extended power Lindley distribution whose CDF and PDF are, respectively, given by

$$\begin{aligned} F(x)=1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }} \,\,\,\, ,\,\, x>0 ;\,\, \beta , \delta , \theta >0 \end{aligned}$$
(1)
$$\begin{aligned} f(x)=\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \,\,\,\, ,\,\, x>0 ; \,\, \beta , \delta , \theta >0 \end{aligned}$$
(2)

Several methods of generating new statistical distributions were presented in the literature review such as, [16, 4], and [3] for more information can you see [12] and [11]. Another important method for generation a new distribution was proposed by [15] named alpha power transformed (APT). Its CDF and PDF are given as:

$$\begin{aligned} G(x,\alpha ,\xi )= {\left\{ \begin{array}{ll} \frac{\alpha ^{F(x,\xi )} -1}{\alpha -1}\,\, ,&{}\text{ if }\,\,\alpha >0,\,\,\alpha \ne 1 \\ F(x,\xi )\,\, , &{}\text{ if }\,\,\alpha = 1 \end{array}\right. } \end{aligned}$$
(3)

and

$$\begin{aligned} g(x,\alpha ,\xi )= {\left\{ \begin{array}{ll} \frac{\log \alpha }{\alpha -1}f(x) \alpha ^{F(x,\xi )}\,\, ,&{}\text{ if }\,\,\alpha \ne 1\\ f(x) \,\, , &{}\text{ if }\,\,\alpha = 1 \end{array}\right. } \end{aligned}$$
(4)

where F(x) and f(x) be the CDF and PDF of a random variable x and \(x>0\).

Several authors utilized APT method to re-extend Lindley distributions in particular cases; for example, [5] introduced the alpha power transformed Lindley (APTL) distribution. Also, [6] presented alpha power transformed inverse Lindley (APTIL) distribution. Whereas alpha power transformed power Lindley (APTPL) distribution was introduced by [9]. Moreover, [7] proposed alpha power transformed power inverse Lindley (APTPIL) distribution.

This study aims to introduce a new lifetime distribution, referred to alpha power transformed extended power Lindley (APTEPL) distribution using the alpha power transformed method to the extended power Lindley (EPL) distribution. This model will be more flexibility in analysing the lifetime data. We are motivated to introduce the (APTEPL) distribution because: (1) It includes a number of well-known lifetime sub-models. (2) It can simulate monotonically increasing, decreasing, constant, bathtub, upside-down bathtub, and increasing - decreasing - increasing hazard rates. and (3) It can be viewed as a suitable model for fitting skewed data that may not be properly fitted by other common distributions, and it can also be used to solve a variety of problems in various fields, such as public health, biomedical studies, and industrial reliability and survival analysis.

The paper is organized as follows: Sect. 1 is introduction. In Sect. 2, the alpha power transformed extended power Lindley (APTEPL) distribution is defined. Some properties of APTEPL distribution are derived in Sect. 3 which includes: \(r^{th}\) moment, moment generating function, Characteristic function , cumulant generating function, ordered statistics and quantiles. The estimation of the unknown parameters by using maximum likelihood estimator are studied in Sect. 4. In Sect. 5, a simulation study is conducted to evaluate the performance of the different estimators. Finally, in Sect. 6 comparison the performance of proposed distribution with other distributions is verified using two real data sets, the first data set represent the waiting time (in minutes) of 100 bank customers and second data set consists of 128 bladder cancer patients.

2 Alpha Power Transformed Extended Power Lindley Distribution

Let \(X\in R^+\) a random variable from extended power Lindley (EPL) distribution [2] with the scale parameter \(\theta >0\) and shape parameters \(\beta ,\delta >0\). By substituting the equations (2) and (1) into (3) and (4), then the CDF and PDF for APTEPL distribution given in the following expression:

$$\begin{aligned} G(x,\alpha ,\beta ,\delta ,\theta )= {\left\{ \begin{array}{ll} \frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}\,\,\, , &{} \text{ if } \alpha \ne 1 \\ \\ 1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\,\,\,, &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(5)

and

$$\begin{aligned} g(x,\alpha ,\beta ,\delta ,\theta )= {\left\{ \begin{array}{ll} \frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}, &{} \text{ if } \alpha \ne 1 \\ \\ \frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }}\,\,\,, &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(6)

The corresponding survival function S(x) and hazard rate function h(x) respectively, as follow:

$$\begin{aligned} S(x,\alpha ,\beta ,\theta )= {\left\{ \begin{array}{ll} \frac{\alpha }{\alpha -1}\left( 1-\alpha ^{-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\right) \,\,, &{} \text{ if } \alpha \ne 1 \\ \\ \left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\,\,, &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(7)

and

$$\begin{aligned} h(x,\alpha ,\beta ,\theta )= {\left\{ \begin{array}{ll} \frac{\theta ^2 \delta \log \alpha }{\theta +\beta }.\frac{x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }}}{\alpha ^{\left( 1+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}-1}\,\,, &{} \text{ if } \alpha \ne 1 \\ \\ \frac{\theta ^2\delta x^{\delta -1}(1+\beta x^{\delta })}{\theta +\beta +\theta \beta x^{\delta }}\,\, , &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(8)

A random variable X that follows alpha power transformed extended power Lindley distribution in (6) was denoted by \(X\sim APTEPL(x,\alpha ,\beta ,\delta ,\theta )\).

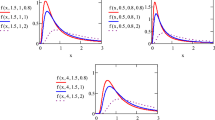
The PDF and HRF plots of \(X\sim APTEPL(x,\alpha ,\beta ,\delta ,\theta )\) are presented in Figs. 1 and 2 respectively,

Fig. 1
figure 1

Plots of the PDF of the APTEPLD for different Values of Its Parameters

Full size image
Fig. 2
figure 2

Plots of the hrf of the APTEPLD for different Values of Its Parameters

Full size image

Also, the reversed hazard rate function r(x) and the cumulative hazard rate function H(x) of the APTEPL distribution are, respectively, given as follows:

$$\begin{aligned} r(x)= {\left\{ \begin{array}{ll} \frac{\frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}}{\frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}} , &{} \text{ if } \alpha \ne 1 \\ \\ \frac{\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }}}{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\,\,\,, &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(9)

and

$$\begin{aligned} H(x)= {\left\{ \begin{array}{ll} -\log \left[ \frac{\alpha }{\alpha -1}\left( 1-\alpha ^{-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\right) \right] \,\,, &{} \text{ if } \alpha \ne 1 \\ \\ - \log \left[ \left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\right] \,\,, &{} \text{ if } \alpha =1 \end{array}\right. } \end{aligned}$$
(10)

2.1 Special Cases

Some well-known distributions are special cases of the APTEPL distribution. We present these cases for selected values of parameters.

  • If \(\alpha =1\) the APTEPL distribution reduces to extended power Lindley (EPL) distribution [2].

  • If \(\delta = 1\) the APTEPL distribution reduces to alpha power transformed extended Lindley (APTEL) distribution. (new)

  • If \(\beta = 1\) the APTEPL distribution reduces to alpha power transformed power Lindley (APTPL) distribution [9].

  • If \(\beta = \delta = 1\) the APTEPL distribution reduces to alpha power transformed Lindley (APTL) distribution [5].

  • If \(\alpha = \beta = 1\) the APTEPL distribution reduces to power Lindley (PL) distribution [8].

  • If \(\alpha = \delta = 1\) the APTEPL distribution reduces to two-parameter Lindley (TPL) distribution [17]

  • If \(\alpha = \beta = \delta = 1\) the APTEPL distribution reduces to the well known Lindley (L) distribution [14].

Table 1 shows the specific values of the parameters used to generate the special cases of APTEPL distribution.

Table 1 The spacial cases of the APTEPL distribution
Full size table

Note: Some spacial cases for the hazard rate function arising from the APTEPL distribution by assigning relevant values of the parameters.

3 Some Mathematical Properties of APTEPL Distribution

This section includes some properties of the APTEPL distribution like, \(r^{th}\) moment, moment generating function, characteristic function, cumulant generating function, and order statistics. and obtain the mean, standard deviation, skewness, kurtosis, and coefficients of variation.

3.1 \(r^{th}\) Moment

The \(r^{th}\) moment of APTEPL distribution is

$$\begin{aligned} {\mu _{r}^{'}}=&E(x^r)=\int _{0}^{\infty } x^{r} f(x,\alpha ,\beta ,\theta ) \,\, dx\nonumber \\ =&\frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }\int _{0}^{\infty }x^{r} x^{\delta -1} (1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\,\, dx \nonumber \\ =&\frac{\alpha \log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }\int _{0}^{\infty } x^{r+\delta -1} (1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\,\, dx \end{aligned}$$
(11)

Using power series ,

$$\begin{aligned} \alpha ^{-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}=\sum _{k=0}^{\infty }(-1)^{k}\frac{(\log \alpha )^{k}\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) ^{k}e^{-\theta k x^{\delta }}}{k!} \end{aligned}$$

Therefore,  (11)  can be written as follows:

$$\begin{aligned} {\mu _{r}^{'}}&=\frac{\alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }\sum _{k=0}^{\infty }\frac{(-1)^{k}(\log \alpha )^{k+1}}{k!} \nonumber \\ {}&\times \int _{0}^{\infty }x^{r+\delta -1}(1+\beta x^{\delta })e^{-\theta (1+k)x^{\delta }}\left( 1+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right) ^{k}\,\,dx \end{aligned}$$
(12)

Also, by using series of Taylor,

$$\begin{aligned} \left( 1+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right) ^{k}=\sum _{l=0}^{k}\left( {\begin{array}{c}k\\ l\end{array}}\right) \left( \frac{\theta \beta x^{\delta }}{\theta +\beta }\right) ^{l} \end{aligned}$$

Hence  (12)  can be expressed as follows:

$$\begin{aligned} {\mu _{r}^{'}}=\frac{\alpha \delta }{\alpha -1}\sum _{k=0}^{\infty }\sum _{l=0}^{k} C_{k,l}\int _{0}^{\infty }x^{r+\delta +\delta l-1}(1+\beta x^{\delta })e^{-\theta (1+k)x^{\delta }}\,\,dx \end{aligned}$$

After some steps we found that

$$\begin{aligned} {\mu _{r}^{'}}=\frac{\alpha }{\alpha -1}\sum _{k=0}^{\infty }\sum _{l=0}^{k} C_{k,l}\left[ \frac{\Gamma (\frac{r}{\delta }+l+1)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+1}}+\beta \frac{\Gamma (\frac{r}{\delta }+l+2)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+2}}\right] \end{aligned}$$
(13)

where :

$$\begin{aligned} C_{k,l}=(-1)^{k} \beta ^{l} \left( {\begin{array}{c}k\\ l\end{array}}\right) \frac{(\log \alpha )^{k+1}}{k!}\frac{\theta ^{l+2}}{(\theta +\beta )^{l+1}} \end{aligned}$$

Remark: the mean of APTEPL distribution is     \(E(X)=\mu ={\mu _{1}^{'}}\)    also, The variance, skewness, kurtosis and coefficient of variation can be obtained by:    \(variance= \sigma ^2=\mu _{2}^{'}-\mu ^{2}\) ; \(\,\,\, skewness=\frac{\mu _{3}}{\sigma ^{3}} =\frac{\mu _{3}^{'}-3\mu _{2}^{'} \mu +2 \mu ^{3}}{(\mu _{2}^{'}- \mu ^{2} )^{(3/2)}}\) ; \(kurtosis=\frac{\mu _{4}}{\sigma ^{2}} =\frac{\mu _{4}^{'}-4\mu _{3}^{'} \mu +6\mu _{2}^{'}\mu ^{2}-2\mu ^{3}}{(\mu _{2}^{'}-\mu ^{2} )^{2}}\)     and     \(CV= \frac{\sigma }{\mu }=\sqrt{\frac{\mu _{2}^{'}}{\mu ^{2}}-1}\)

3.2 Moment Generating Function, Characteristic Function and Cumulant Generating Function

  • The moment generating function is given by

    $$\begin{aligned} M_{X}(t)&=E(e^{tx})\nonumber \\ {}&=\int _{0}^{\infty }e^{tx}f(x)\,\,df\nonumber \\&=\sum _{r=0}^{\infty }\frac{t^{r}}{r!}\int _{0}^{\infty }x^{r} f(x,\alpha ,\beta ,\theta ) \,\, dx\nonumber \\&=\sum _{r=0}^{\infty }\frac{t^{r}}{r!}\mu _{r}^{'} \end{aligned}$$
    (14)

    In case of using the equations (13) and (14) we found that moment generating function of APTEPL distribution can be expressed as follows:

    $$\begin{aligned} M_{X}(t)=\frac{\alpha }{\alpha -1}\sum _{k=0}^{\infty }\sum _{l=0}^{k} C_{k,l}\frac{t^{r}}{r!}\left[ \frac{\Gamma (\frac{r}{\delta }+l+1)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+1}}+\beta \frac{\Gamma (\frac{r}{\delta }+l+2)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+2}}\right] \end{aligned}$$
    (15)

  • The Characteristic function is given by

    $$\begin{aligned} \phi _{X}(t)=E(e^{itx})=\int _{0}^{\infty }e^{itx}f(x)\,\,df \end{aligned}$$

    similarly, after some steps the Characteristic function can be expressed:

    $$\begin{aligned} \phi _{X}(t)=\frac{\alpha }{\alpha -1}\sum _{k=0}^{\infty }\sum _{l=0}^{k} C_{k,l}\frac{(it)^{r}}{r!}\left[ \frac{\Gamma (\frac{r}{\delta }+l+1)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+1}}+\beta \frac{\Gamma (\frac{r}{\delta }+l+2)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+2}}\right] \end{aligned}$$
    (16)

    where    \(i=\sqrt{-1}\)

  • The Cumulant generating function is given by:

    $$\begin{aligned} K(t)=\log \phi _{X}(t) \end{aligned}$$
    (17)

    In case of using the equations (16) and (17) we found that cumulant generating function of APTEPL distribution can be expressed:

    $$\begin{aligned} K(t)=\log \left( \frac{\alpha }{\alpha -1}\right) +\log C \end{aligned}$$
    (18)

    where:

    $$\begin{aligned} C=\sum _{k=0}^{\infty }\sum _{l=0}^{k} C_{k,l}\frac{(it)^{r}}{r!}\left[ \frac{\Gamma (\frac{r}{\delta }+l+1)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+1}}+\beta \frac{\Gamma (\frac{r}{\delta }+l+2)}{\left[ \theta (1+k)\right] ^{\frac{r}{\delta }+l+2}}\right] \end{aligned}$$

3.3 Quantile Function

The quantile function of the APTEPL distribution random variable X is \(Q_{X}(u)=G_{X}^{-1}(u)\) , \(0<u<1\), and for any \(\alpha ,\beta ,\delta ,\theta >0\) and \(\alpha \ne 1\). In the following steps, we find out the expression of \(Q_{X}\).

By considering the \(p=1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\), the CDF of APTEPL distribution (5) can be written as

$$\begin{aligned} G(x,\alpha , \beta , \delta , \theta )= \frac{\alpha ^p-1}{\alpha -1} \end{aligned}$$
(19)

By solving \(G_{X}(x)=u\) for p, we get

$$\begin{aligned} u&= \frac{\alpha ^p-1}{\alpha -1}\nonumber \\ u(\alpha -1)&=\alpha ^p-1\nonumber \\ \alpha ^p&=u(\alpha -1)+1\nonumber \\ p \log (\alpha )&=\log (u(\alpha -1)+1)\nonumber \\ p&=\frac{\log (u(\alpha -1)+1)}{\log (\alpha )} \end{aligned}$$
(20)

By solving \(p=1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\) for x, we obtain

$$\begin{aligned} p-1&=-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\nonumber \\ \left( p-1\right) \left( \frac{\theta +\beta }{\beta }\right)&=-\left( \frac{\theta +\beta }{\beta }+\theta x^{\delta }\right) e^{-\theta x^{\delta }}\nonumber \\ \left( p-1\right) \left( \frac{\theta +\beta }{\beta }\right) e^{-\left( \frac{\theta +\beta }{\beta }\right) }&=-\left( \frac{\theta +\beta }{\beta }+\theta x^{\delta }\right) e^{-\left( \frac{\theta +\beta }{\beta }+\theta x^{\delta }\right) } \end{aligned}$$
(21)

By using negative Lambert \(W_{-1}\) function, from (21) we get

$$\begin{aligned} -\left( \frac{\theta +\beta }{\beta }+\theta x^{\delta }\right) =W_{-1}\left( \left( p-1\right) \left( \frac{\theta +\beta }{\beta }\right) e^{-\left( \frac{\theta +\beta }{\beta }\right) }\right) \end{aligned}$$
(22)

From (22) and put \(Q_{X}(u)=x\), we obtain

$$\begin{aligned} Q_{X}(u)=\left\{ -\frac{1}{\beta }-\frac{1}{\theta }-\frac{1}{\theta } W_{-1}\left( \left( p-1\right) \left( \frac{\theta +\beta }{\beta }\right) e^{-\left( \frac{\theta +\beta }{\beta }\right) }\right) \right\} ^{\frac{1}{\delta }} \end{aligned}$$
(23)

By substituting (20) into (23), then the quantile function \(Q_{X}(u)\) is given as

$$\begin{aligned} Q(u)=\left\{ -\frac{1}{\beta }-\frac{1}{\theta }-\frac{1}{\theta }W_{-1}\left( \left[ \frac{\log (u(\alpha -1)+1)}{\log (\alpha )}-1\right] \left( \frac{\theta }{\beta }+1\right) e^{-\left( \frac{\theta }{\beta }+1\right) }\right) \right\} ^{\frac{1}{\delta }} \end{aligned}$$
(24)

whereas \(W_{-1}(.)\) is the negative Lambert W function and \(u\in (0,1)\). Further, the first quantile   Q1   obtained by substituting   \(u=0.25\)   in (24). The median   Q2   and third quantile   Q3   obtained in a similar manner. Tables 2 and 3 show behavior the first three quartiles of APTEPL distribution with the different values of Its parameters. We observed that if value of \(\alpha ,\,\beta , \, \text {and} \, \delta\) are constant,while value of \(\theta\) increases, value of each of Q1, Q2 and Q3 decrease. But in the case of values of \(\beta ,\,\delta ,\, \text {and} \,\theta\) are fixed, values of Q1, Q2 and Q3 increase when value of \(\alpha\) increases. Also, in the case of value of \(\beta\) increases, whereas values of \(\alpha ,\,\delta ,\, \text {and} \, \theta\) are fixed , values of each of Q1, Q2 and Q3 increase too. Finally, values of each of Q1, Q2 and Q3 increase when value of \(\delta\) increases, while value of \(\alpha ,\,\beta , \,\text {and}\, \theta\) are constant.

Table 2 \(1^{st}\) quantile (Q1), median (Q2) and \(3^{rd}\) quantile (Q3) when \(\delta =0.5\) and different values of the other parameters of APTEPL distribution
Full size table
Table 3 \(1^{st}\) quantile (Q1), median (Q2) and \(3^{rd}\) quantile (Q3) when \(\delta =2\) and different values of the other parameters of APTEPL distribution
Full size table

3.4 Order Statistics

Let \(X_{(i)}, i =1,2,......., n\) denoted to n independent random variables from any distribution with CDF \(F_{X} (x)\) and PDF \(f_{X} (x)\), then the PDF of \(X_{(i)}\) is given by :

$$\begin{aligned} f_{X_{(i)}}(x)=\frac{n!}{(i-1)!(n-i)!} f_{X}(x)\left[ F_{X}(x)\right] ^{i-1}\left[ 1-F_{X}(x)\right] ^{n-i}\,\,\,;i=1,2,..,n \end{aligned}$$
(25)

In case of substituting (6) and (5) into equation (25), the PDF of \(X_{i}\) according to APTEPL distribution given as the following:

$$\begin{aligned} f_{X_{(i)}}(x)=\frac{n!}{(i-1)!(n-i)!} \frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}}\nonumber \\ \,\,\,\times \left[ \frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}\right] ^{i-1}\times \left[ 1-\frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}\right] ^{n-i} \end{aligned}$$
(26)

Now, the PDF of \(X_{(n)}\) and \(X_{(1)}\) respectively, given by :

$$\begin{aligned} f_{X_{(n)}}(x)=n\,\frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{\left[ 1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\right] }\nonumber \\\,\,\,\times \left[ \frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}\right] ^{n-1} \end{aligned}$$
(27)

and

$$\begin{aligned} f_{X_{(1)}}(x)=n\,\frac{\log \alpha }{\alpha -1}\frac{\theta ^2\delta }{\theta +\beta }x^{\delta -1}(1+\beta x^{\delta })e^{-\theta x^{\delta }} \alpha ^{\left[ 1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\right] }\nonumber \\\,\,\,\times \left[ 1-\frac{\alpha ^{1-\left( 1+\frac{\beta \theta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}} -1}{\alpha -1}\right] ^{n-1} \end{aligned}$$
(28)

4 Simulation Study

The simulation study for MLEs of APTEPL distribution is performed by generating \(N=1000\) samples of sizes \(n=20, 40,\,\,80,\,\, and \,\, 100\) from APTEPL distribution and studied the behavior of estimates, based on certain measures, which are mean square errors (MSEs) and absolute biases (ABs). Considering CDF of APTEPL distribution and after performing mathematical calculations it was found that if u is a random number from U(0, 1), then

$$\begin{aligned} x=\left\{ -\frac{1}{\beta }-\frac{1}{\theta }-\frac{1}{\theta }W_{-1}\left( \left[ \frac{\log (u(\alpha -1)+1)}{\log \alpha }-1\right] \left( \frac{\theta +\beta }{\beta }\right) e^{-\left( \frac{\theta }{\beta }+1\right) }\right) \right\} ^\frac{1}{\delta } \end{aligned}$$
(29)

of the APTEPL distribution with parameters \(\alpha ,\beta ,\delta ,\) and \(\theta\). where \(W_{-1}(.)\) is the negative Lambert W function.

Tables 4 and 5 show the empirical results of a simulation study using MLEs and the goodness.fit() function in the \('AdequacyModel'\) package via the R program. The MSEs and ABs decrease as the sample size increases.

Table 4 Simulation results: MSEs and ABs
Full size table
Table 5 Simulation results: MSEs and ABs
Full size table

5 Maximum Likelihood Estimator

Let \(X= ( x_{1}, x_{2}, ........, x_{n} )\) be the random variables of size n belong to \(APTEPL( x,\alpha ,\beta ,\delta , \theta )\), then the Likelihood function can be written as,

$$\begin{aligned} L=\prod _{i=1}^{n}f(x, \alpha ,\beta , \delta ,\theta ) \end{aligned}$$
(30)

Substituting (6) into (30) and taking the logarithm function for two side we found that the \(Loglikelihood\,\, function\) is given by:

$$\begin{aligned} \log L&= n\log (\log (\alpha ))+2n\log \theta +n\log \delta -n\log (\alpha -1)-n\log (\theta +\beta )\nonumber \\ {}&+\sum _{i=1}^{n}\log x^{\delta -1}+\sum _{i=1}^{n}\log (1+\beta x^{\delta })-\theta \sum _{i=1}^{n}x^{\delta }\nonumber \\ {}&+\sum _{i=1}^{n}\left[ 1-\left( 1+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\right] \log (\alpha ) \end{aligned}$$
(31)

By taking the partial derivative for Log L in (31) with respected to \(\alpha ,\theta , \beta \, \text {and} \, \delta\) respectively , we got that

$$\begin{aligned} \frac{\partial \log L}{\partial \alpha }&=\frac{n}{\alpha \log \alpha }- \frac{n}{\alpha -1}+\frac{1}{\alpha }\sum _{i=1}^{n}\left[ 1-\left( 1+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right) e^{-\theta x^{\delta }}\right] \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial \log L}{\partial \theta }&=\frac{2n}{\theta }- \frac{n}{\theta +\beta }-\sum _{i=1}^{n} x^{\delta } +\log (\alpha ) \sum _{i=1}^{n}\left[ 1-\left( \frac{\beta }{\theta +\beta }\right) ^{2}+\frac{\theta \beta x^{\delta }}{\theta +\beta }\right] x^{\delta }e^{-\theta x^{\delta }} \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial \log L}{\partial \beta }&=-\frac{n}{\theta +\beta }+\sum _{i=1}^{n}\frac{x^{\delta }}{1+\beta x^{\delta }}+\log (\alpha )\,\,\sum _{i=1}^{n}\left[ \frac{\theta ^2 x^{\delta }}{(\theta +\beta )^2}e^{-\theta x^{\delta }}\right] \end{aligned}$$
(34)
$$\begin{aligned} \frac{\partial \log L}{\partial \delta }&=\frac{n}{\delta }+\sum _{i=1}^{n}\frac{x^{\delta -1}\log x}{x^{\delta -1}}+\sum _{i=1}^{n}\frac{\beta x^{\delta }\log x}{1+\beta x^{\delta }}-\theta \sum _{i=1}^{n}x^{\delta }\log x \nonumber \\&+ \log (\alpha )\,\,\sum _{i=1}^{n}\left[ \frac{1+\theta \beta x^{\delta }}{\theta +\beta }\theta ^2 x^{\delta } e^{-\theta x^{\delta }} \log x \right] \end{aligned}$$
(35)

The maximum likelihood estimator of \(\alpha\) ,\(\theta\) , \(\beta\) and \(\delta\) can be obtained by solving the above four nonlinear equations when \(\frac{\partial \log L}{\partial \alpha }=0\), \(\frac{\partial \log L}{\partial \theta }=0\) , \(\frac{\partial \log L}{\partial \beta }=0\) and \(\frac{\partial \log L}{\partial \delta }=0\) with using the numerical approach.

6 Application

In this section, two real data sets are used to compare the performance of proposed APTEPL distribution with three existing models: alpha power transformed power Lindley (APTPL) distribution [9] , alpha power transformed extend Lindley (APTEL) which is as spacial case of our proposed distribution and alpha power transformed Lindley (APTL) distribution [5]. To compare the performance of our model with the others models the following criterions are used: Akaike information criterion (AIC), Bayesian information criterion (BIC), Corrected Akaike information criterion (AICc), and Kolmogorov-Smirnov goodness of fit test (KS). The distribution with the smallest values of \(AIC, BIC,\,\, \text {and} \,\, AICc\) or maximum \(p-value\) for (KS) test is considering as the best model for the given data. In this section the numerical results are obtained by using of R software.

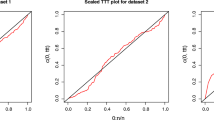
First data set taken from Ijaz Muhammad et al. [10]. The data set represent the waiting time (in minutes) of 100 bank customers. The MLE of the parameters and standard errors and goodness of fit statistics of the model parameters are provided in Tables 6 and 7. It is clear from Table 7 that the APTEPL distribution gives better fit than the other distributions. Figure 3 shows the theoretical and empirical \(PDF\,\, \text {and} \,\,CDF\) of the \(APTEPL, APTPL, APTEL,\,\, \text {and} \,\, APTL\) distributions using Bank customer data.

Table 6 MLEs and SE of parameters for data set 1
Full size table
Table 7 Measure of \(-logL,\, AIC,\, BIC,\, AICc,\, KS \,\, \text {and} \,\, P-value (KS)\) for data set 1
Full size table
Fig. 3
figure 3

plots of the estimated PDFs and CDFs of APTEPL distribution and other distributions for data set 1

Full size image

Second data set consists of 128 bladder cancer patients taken from Lee Elisa et al. [13] and used by Ahmad et al. [1]. The MLEs of the parameters and standard errors and goodness of fit statistics of the model parameters are provided in Table 8 and 9, from Table 9 it can be that the APTEPL distribution gives better fit than the other distributions. Figure 4 shows the theoretical and empirical PDF and CDF of the \(APTEPL, APTPL, APTEL,\,\, \text {and} \,\, APTL\) distributions regarding data set 2.

Table 8 MLEs and SE of parameters for data set 2
Full size table
Table 9 Measure of \(-logL,\, AIC,\, BIC,\, AICc,\, KS \,\, \text {and}\,\, P-value(KS)\) for set 2
Full size table
Fig. 4
figure 4

plots of the estimated PDFs and CDFs of APTEPL distribution and other distributions for data set 2

Full size image

7 Conclusion

In this article, we have proposed alpha power transformation extended power Lindley distribution which is extension of extended power Lindley distribution using alpha power transformation. Some properties of the proposed distribution are derived such as moments, moment generating function, Characteristic function , cumulant generating function, quantiles and order statistics. From the proposed distribution various distributions related to Lindley distribution can be obtained as a special cases of it. If \(\beta =1\) alpha power transformed power Lindley is obtained, similarly, if \(\delta =1\) alpha power transformed extended Lindley, if \(\beta =1\) and \(\delta =1\) alpha power transformed Lindley, if \(\alpha =1\) extended power Lindley, if \(\alpha =1\) and \(\beta =1\) power Lindley, if \(\alpha =1\) and \(\delta =1\) extended Lindley and if \(\alpha =1\), \(\beta =1\) and \(\delta =1\) Lindley distribution are obtained. The performance of the proposed distribution is verified by using real data sets and performing simulation study. It was observed that the proposed distribution is good w.r.t the comparing criterions \(AIC, BIC \,\, \text {and}\,\, AICc\). Therefore it was better than other models considered in this article. It works well for the real life data to model the waiting time (in minutes) of 100 bank customers data and the data of 128 bladder cancer patients.