1 Introduction

It is well known that the celebrated nonlinear Schrödinger (NLS) equation [23]

$$\begin{aligned} \textrm{i}q_t+\frac{1}{2}q_{xx}+|q|^{2}q=0 \end{aligned}$$

can be used to model short soliton pulses in nonlinear optics [1]. To model ultrashort optical pulses, one has to modify the NLS equation and establish new equations. Based on this observation, Kodama and Hasegawa proposed the following higher-order nonlinear Schrödinger (HNLS) equation

$$\begin{aligned} iq_{\eta }+\alpha _{1}q_{\xi \xi }+\alpha _{2}|q|^{2}q+i[\beta _{1}q_{\xi \xi \xi }+\beta _{2}|q|^{2}q_{\xi }+\beta _{3}q(|q|^{2})_{\xi }]=0, \end{aligned}$$

where \(q(\xi ,\eta )\) is a complex-valued function, \(\alpha _{1},\alpha _{2},\beta _{j}, j=1,2,3\) are real constants [8]. Generally speaking, the HNLS equation is not integrable unless some restrictions are imposed on \(\beta _{j} (j=1,2,3)\). Sasa and Satsuma [15] consider the following integrable case

$$\begin{aligned} iq_{\eta }+\frac{1}{2}q_{\xi \xi }+|q|^{2}q+iq_{\xi \xi \xi }+6i|q|^{2}q_{\xi }+3{i}q(|q|^{2})_{\xi }=0. \end{aligned}$$
(1)

Through gauge, Galilean and scale transformations, The Eq. (1) is transformed to a complex modified KdV-type equation

$$\begin{aligned} q_{t}+q_{xxx}+6|q|^2q_{x}+3q(|q|^2)_x=0, \end{aligned}$$
(2)

The Eq. (2) is commonly known as Sasa–Satsuma equation, which has been widely studied with various methods such as the inverse scattering scheme [7, 15], Hirota’s bilinear approach [5], Darboux transform [12, 21] and Bäcklund transform [20]. Recently Feng [4] and Yang [22] Studied the Rogue wave of Sasa–Satsuma equation. Much research has been conducted for it, we will not dwell on a detailed exposition of various results.

The aim of this paper is to study higher-order soliton solutions for the Sasa–Satsuma equation by means of \(\bar{\partial }\) method [3, 11, 17, 24]. Soliton solutions corresponding to multiple poles have been investigated in the literature before. Zakharov first given a soliton solution for the NLS equation corresponding to a double pole [23]. Subsequently higher-order soliton solutions have also been studied for the modified KdV equation [19], the sine-Gordon equation [18]. So far various methods have been developed to deal with higher-order solitons, for example the inverse scattering scheme [10, 13, 16, 18, 19, 23], generalized Darboux transform [6], robust inverse scattering transform [14] et al. The motivation of this paper is as follows.

  1. 1.

    Compared with the Riemann–Hilbert method, the \(\bar{\partial }\) method is more directly to derive the soliton solutions. In particular, we will show that \(\bar{\partial }\) method is also a powerful tool to obtain higher-order soliton solutions.

  2. 2.

    Compared to the previous results under the \(\bar{\partial }\) method [10], we will consider more general higher-order soliton solutions and the interaction related to one simple pole and the other one double pole.

This paper is arranged as follows. In Sect. 2, we summary \(\bar{\partial }\)-method for the Sasa–Satsuma equation. In Sect. 3, we derive the explicit determinant form of a higher-order soliton solution which corresponds to one p-th order pole, as well as the interaction related to one simple pole and one double pole is displayed.

2 Summary of \(\bar{\partial }\)-Method for the Sasa–Satsuma Equation

We summarize the already well-known results for the Sasa–Satsuma Eq. (2) that will be used in our study. Here we consider the Sasa–Satsuma equation with zero boundary condition (ZBC) at \(|x|\rightarrow \infty\). To be more precise, q(x, t) decays rapidly for large |x|. The Eq. (2) can be viewed as a compatible condition of the following linear differential equations (also called Lax pair)

$$\begin{aligned} \psi _x(x,t,k)=X\psi (x,t,k),\qquad \psi _t(x,t,k)=T\psi (x,t,k), \end{aligned}$$
(3)

where

$$\begin{aligned} \begin{aligned} X&=-\textrm{i}kJ_1+Q,\\ T&=-4\textrm{i}k^{3}J_1+4k^2Q+2\textrm{i}kJ_1(Q_{x}-Q^2)-Q_{xx}+Q_{x}Q-QQ_{x}+2Q^3 \end{aligned} \end{aligned}$$

and

$$\begin{aligned} J_1=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -1 \\ \end{array} \right) ,\quad Q=\left( \begin{array}{ccc} 0 &{} q &{} \bar{q} \\ -\bar{q} &{} 0 &{} 0 \\ -q&{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Here the bar denotes complex conjugate and q means q(x, t). In order to establish a connection between Lax pair and \(\bar{\partial }\) problem, we first consider a priori [2] \(\psi (x,t,k)\) for the Eq. (3) which obey the boundary condition

$$\begin{aligned} \psi (x,t,k)\rightarrow {e^{-(\textrm{i}k{x}+4\textrm{i}k^3{t})J_1}},\quad x\rightarrow \infty \end{aligned}$$
(4)

for all \(\textrm{Im}\{k\}\ne 0\). We introduce a modified priori

$$\begin{aligned} \Psi (x,t,k)=\psi (x,t,k){e^{(\textrm{i}k{x}+4\textrm{i}k^3{t})J_1}}, \end{aligned}$$

then \(\Psi (x,t,k)\) satisfies

$$\begin{aligned} \Psi (x,t,k)\rightarrow {{I}},\quad x\rightarrow \infty \end{aligned}$$
(5)

and

$$\begin{aligned} \begin{aligned} \Psi _{{x}}=&-\textrm{i}k[J_1,\Psi ]+{Q}\Psi ,\\ \Psi _{{t}}=&-4\textrm{i}k^{3}[J_1,\Psi ]+4k^2Q\Psi +2\textrm{i}kJ_1(Q_{x}-Q^2)\Psi \\&-(Q_{xx}-Q_{x}Q+QQ_{x}-2Q^3)\Psi . \end{aligned} \end{aligned}$$
(6)

Moreover, we know that \(\Psi (x,t,k)\) and \(\psi (x,t,k)\) are analytic in \(\mathbb {C}/{\mathbb {R}}\), then we can write an asymptotic expansion for \(\Psi (x,t,k)\) when \(k\rightarrow {\infty }\)

$$\begin{aligned} \Psi (x,t,k)=\Psi _{0}(x,t)+\frac{\Psi _{1}(x,t)}{k}+\frac{\Psi _{2}(x,t)}{k^2}+O(\frac{1}{k^3}). \end{aligned}$$

Substituting the above expansion into the Eq. (6) and using (5), we have

$$\begin{aligned} \Psi (x,t,k)\rightarrow {{I}},\quad |k|\rightarrow \infty . \end{aligned}$$
(7)

2.1 \(\bar{\partial }\)-Problem Related to the Sasa–Satsuma Equation

Based on the above analysis, we start from an integral form of the \(3\times 3\) matrix \(\bar{\partial }\) problem \(\bar{\partial }\Psi (k,\bar{k})=\Psi (k,\bar{k}){R(k,\bar{k})}\) with the canonical normalization (7) in the complex k-plane

$$\begin{aligned} \Psi (k,\bar{k})=I+\Psi (k,\bar{k})R(k,\bar{k})C_{k}, \end{aligned}$$
(8)

where \(R(k,\bar{k})\) is a spectral transform matrix and \(C_k\) is the Cauchy-Green integral operator acting on the left and given by

$$\begin{aligned} \Psi (k)R(k)C_{k}=\frac{1}{2\pi {\textrm{i}}}\iint \frac{dl\bigwedge {d{\bar{l}}}}{l-k}\Psi (l,\bar{l})R(l,\bar{l}). \end{aligned}$$

For the sake of simplicity, the arguments \(\bar{k}\) have omitted in the \(\Psi (k,\bar{k})\) and \(R(k,\bar{k})\) from now on. A formal solution of (8) is given by

$$\begin{aligned} \Psi (k)=I\cdot (I-R(k)C_k)^{-1}. \end{aligned}$$
(9)

To establish a connection with Lax pair, we need to introduce the variables x, t into the spectral transform matrix R(k). For the Sasa–Satsuma equation, we assume that R(k) satisfies

$$\begin{aligned} R_{x}(x,t,k)&=-\textrm{i}k[J_1,R(x,t,k)], \end{aligned}$$
(10a)
$$\begin{aligned} R_{t}(x,t,k)&=-4\textrm{i}k^{3}[J_1,R(x,t,k)], \end{aligned}$$
(10b)

From (8), (9) and (10a) we arrive at the first expression of the Eq. (6) and

$$\begin{aligned} Q(x,t)=-\textrm{i}[J_1,\langle {\Psi {R}}\rangle ], \end{aligned}$$
(11)

or

$$\begin{aligned} q(x,t)=-2\textrm{i}\langle {\Psi {R}}\rangle _{12}, \end{aligned}$$
(12)

where

$$\begin{aligned} \langle {F},G\rangle =\frac{1}{2\pi {\textrm{i}}}\iint {F(\ell )}G^{T}(\ell )d\ell \wedge {d\bar{\ell }}, \end{aligned}$$

and \(\langle {\Psi {R}}\rangle =\langle {\Psi {R}},I\rangle\). The time evolution equation of \(\Psi (x,t,k)\) is implied by (10b) and given by the second expression of the Eq. (6). The above detailed calculations are available in [24]. In fact, the Eq. (6) can be viewed as the another form of Lax pair associated with the Sasa–Satsuma equation.

2.2 Symmetry Conditions and Discrete Spectrum

It is well known that the function \(\Psi (x,t,k)\) in (6) admits the following symmetries [16]

$$\begin{aligned} \Psi (x,t,k)=J_2\overline{\Psi (x,t,-\bar{k})}J_2,\quad \Psi ^{-1}(x,t,k)=\Psi ^{\dagger }(x,t,\bar{k}), \end{aligned}$$
(13)

where the superscript \(\dagger\) means the Hermitian conjugation and

$$\begin{aligned} J_2=\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ \end{array} \right) . \end{aligned}$$

From the uniqueness of \(\bar{\partial }\) problem the spectral transform matrix R(x, t, k) satisfies

$$\begin{aligned} R(x,t,k)=J_2\overline{R(x,t,-\bar{k})}J_2,\quad R(x,t,k)=R^{\dagger }(x,t,\bar{k}). \end{aligned}$$
(14)

So we have, elementwise,

$$\begin{aligned} R_{13}(k)=\overline{{R}_{12}(-\bar{k})},\quad R_{21}(k)=\overline{{R}_{12}(\bar{k})},\quad R_{31}(k)=R_{12}(-k). \end{aligned}$$
(15)

Suppose that \(R_{12}(x,t,k)\) has a finite simple pole \(k_{j}~(j=1,2,\ldots ,N)\). Owing to the symmetry conditions (15), the discrete spectrum is the set

$$\begin{aligned} Z=\{k_{j},-\bar{k}_{j},\bar{k}_{j},-k_{j}\}. \end{aligned}$$
(16)

In particular, If \(k_{j}\) is a pure imaginary number, i.e. \(k_j=\textrm{i}\lambda _j\), the discrete spectrum set reduces to

$$\begin{aligned} Z=\{\textrm{i}\lambda _j,-\textrm{i}\lambda _j\}. \end{aligned}$$
(17)

2.3 N-Soliton Solutions for the Sasa–Satsuma Equation

In this subsection we consider soliton solutions for the Sasa–Satsuma equation. From the theory of the inverse scattering transform we know that the poles of the reflection coefficient give rise to soliton solutions. Here soliton solutions correspond to the spectral transform matrix R(k) located at the discrete spectrum points of the complex plane where a solution \(\Psi (k)\) of the \(\bar{\partial }\) problem has simple poles. Firstly we consider the discrete spectrum set Z (17), by means of the Eq. (10) and the symmetry conditions (15), we can choose

$$\begin{aligned} \begin{aligned} R(x,t,k)&= e^{-\textrm{i}(k{x}+4k^3{t})J_1}R_0e^{\textrm{i}(k{x}+4k^3{t})J_1},\\ R_0&= \pi \sum ^{N}_{j=1}\left( \begin{array}{ccc} 0 &{} c_{1j}\delta (k-\textrm{i}\lambda _j) &{} c_{2j}\delta (k-\textrm{i}\lambda _j) \\ c_{3j}\delta (k+\textrm{i}\lambda _j) &{} 0 &{} 0 \\ c_{4j}\delta (k+\textrm{i}\lambda _j) &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned} \end{aligned}$$
(18)

where \(\delta (k)\) denotes the delta function and \(c_{1j},c_{2j},c_{3j},c_{4j}~(j=1,2,\ldots ,N)\) are given by the following proposition.

Proposition 1

Let \(c_{1j}=\gamma _j\), \(\gamma _j\) is arbitrary complex constant, then the coefficients \(c_{2j},c_{3j},c_{4j}\) are given as follow

$$\begin{aligned} c_{2j}=c_{3j}=-\bar{\gamma }_j,\quad c_{4j}=c_{1j}=\gamma _j. \end{aligned}$$
(19)

Proof

It follows from \({R}_{21}(k)=\overline{{{R}}_{12}(\bar{k})}\) that \(R_0^{21}(k)=\overline{R_{0}^{12}(\bar{k})}\), this is

$$\begin{aligned} \overline{R_{0}^{12}(\bar{k})}=\overline{c_{1j}\delta (\bar{k}-\textrm{i}\lambda _j)},\quad R_0^{21}(k)=c_{3j}\delta (k+\textrm{i}\lambda _j). \end{aligned}$$

Let \(-\frac{1}{2\textrm{i}}\iint {f(\ell )}\bullet {d\ell }\wedge {d\bar{\ell }}\) act on \(R_0^{21}(k)=\overline{R_{0}^{12}(\bar{k})}\) and take advantage of the formula

$$\begin{aligned} \iint {f}(\ell ,\bar{\ell })\delta (\ell -k){d}{\ell }\wedge {d\bar{\ell }}=-2\textrm{i}{f(k,\bar{k})}, \end{aligned}$$

we derive

$$\begin{aligned} c_{3j}=-\bar{\gamma }_{j}. \end{aligned}$$
(20)

In the similar way, we can obtain

$$\begin{aligned} c_{2j}=-\bar{\gamma }_{j},\quad c_{4j}=\bar{\gamma }_{j}. \end{aligned}$$
(21)

thus we have (19). \(\square\)

Plugging (18) into (12), we can derive

$$\begin{aligned} q=-2\textrm{i}G\Psi _{11}^{T}, \end{aligned}$$
(22)

where G and \(\Psi _{11}\) are N-dimension row vector

$$\begin{aligned} \begin{aligned} G&=(\gamma _1e^{\theta _1},\gamma _2{e^{\theta _2}},\ldots ,\gamma _j{e^{\theta _j}},\ldots ,\gamma _{N}{e^{\theta _N}}),\quad \theta _j=2(\lambda _j{x}-4\lambda ^3_{j}t),\\ \Psi _{11}&=(\psi _{11}(\textrm{i}\lambda _1),\psi _{11}(\textrm{i}\lambda _2),\ldots ,\psi _{11}(\textrm{i}\lambda _j),\ldots ,\psi _{11}(\textrm{i}\lambda _N)), \end{aligned} \end{aligned}$$

and substituting the explicit form of R(k) (18) into the equation in the integral form (8), we derive a linear algebraic system

$$\begin{aligned} (I+\Gamma )\Psi _{11}^{T}=E, \quad \Gamma =\bar{\Gamma }_1\Gamma _1+\Gamma _2\bar{\Gamma }_2, \end{aligned}$$
(23)

where I denotes the identity matrix, E is an N-dimensional column vector with an element of 1 and

$$\begin{aligned} \Gamma _1=\Gamma _2,\quad (\Gamma _1)_{ij}=\frac{\gamma _je^{\theta _j}}{\textrm{i}(\lambda _i+\lambda _j)}. \end{aligned}$$

From (22) and (23), we can obtain the determinant form for N-soliton solution

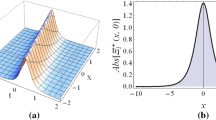
$$\begin{aligned} q=-2\textrm{i}\frac{\textrm{det}\Omega ^{\prime }}{\textrm{det}\Omega },\quad \Omega =I+\Gamma ,\quad \Omega ^{\prime }=\left( \begin{array}{cc} 0 &{} G \\ E &{} \Omega \\ \end{array} \right) . \end{aligned}$$
(24)

For example, we take \(N=1\), the 1-soliton solution is

$$\begin{aligned} q=\textrm{i}e^{\chi +\textrm{i}\nu }sech(\mu -\chi +2\theta _1) \end{aligned}$$

where

$$\begin{aligned} \gamma _1=\mu +\textrm{i}\nu ,\quad \lambda _1=\frac{\sqrt{2}}{2}e^{\chi } \end{aligned}$$

and displayed in Fig. 1a.

For the general case (16), similar to the proposition 2.1, we take

$$\begin{aligned} R_0(k)=\pi \sum ^{N}_{j=1}\left( \begin{array}{ccc} 0 &{} \alpha _j\mu ^{+}_{j}+\beta _j\nu ^{-}_{j} &{} -\bar{\alpha }_j\nu ^{-}_{j}-\bar{\beta }_j\mu ^{+}_{j} \\ -\bar{\alpha }_j\nu ^{+}_{j}-\bar{\beta }_j\mu ^{-}_{j} &{} 0 &{} 0 \\ \alpha _j\mu ^{-}_{j}+\beta _j\nu ^{+}_{j} &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$
(25)

where \(\mu ^{\mp }_{j}=\delta (k\pm {k}_j)\), \(\nu ^{\mp }_{j}=\delta (k\pm {\bar{k}_j})\) and \(\alpha _j,\beta _j~(j=1,2,\ldots ,N)\) are arbitrary complex values. As the above process, plugging (25) into (12), we can derive

$$\begin{aligned} q=-2\textrm{i}\hat{G}\hat{\Psi }_{11}^{T}, \end{aligned}$$
(26)

where G and \(\Psi _{11}\) are 2N-dimensional row vector

$$\begin{aligned} \begin{aligned} \hat{G}&=(\alpha _1g_1,\beta _1\bar{g}_1,\ldots ,\alpha _j{g_j},\beta _j\bar{g}_j,\ldots ,\alpha _{N}{g_N},\beta _N\bar{g}_N),\quad {g}_j=e^{-2\textrm{i}(k_j{x}+4k^3_j{t})},\\ \hat{\Psi }_{11}&=(\psi _{11}(k_1),\psi _{11}(-\bar{k}_1),\ldots ,\psi _{11}(k_j),\psi _{11}(-\bar{k}_j),\ldots ,\psi _{11}(k_N),\psi _{11}(-\bar{k}_N)). \end{aligned} \end{aligned}$$

Next substituting the explicit form of R(k) (25) into the equation in the integral form (8), we derive the linear algebraic system (23), where I denotes the identity matrix, E is an 2N-dimensional column vector with an element of 1 and \(\Gamma _j, j=1,2\) are the block matrix \(\Gamma _{j}=(\Gamma ^{(mn)}_{j})_{N\times {N}}\),

$$\begin{aligned} \begin{aligned} \Gamma ^{(mn)}_1=\left( \begin{array}{cc} \frac{\alpha _{n}{g}_n}{k_n-\bar{k}_m}&{} \frac{\beta _{n}\bar{g}_n}{-\bar{k}_n-\bar{k}_m} \\ \frac{\alpha _{n}{g}_n}{k_n+k_m} &{} \frac{\beta _{n}\bar{g}_n}{-\bar{k}_n+k_m} \\ \end{array} \right) ,\quad \Gamma ^{(mn)}_2=\left( \begin{array}{cc} \frac{{\beta }_{n}\bar{g}_n}{k_n-\bar{k}_m}&{} \frac{\alpha _{n}{g}_n}{-{k}_n-{k}_m} \\ \frac{{\beta }_{n}\bar{g}_n}{\bar{k}_n+\bar{k}_m} &{} \frac{\alpha _{n}{g}_n}{-k_n+\bar{k}_m} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

So we can obtain the determinant form for N-soliton solution

$$\begin{aligned} q=-2\textrm{i}\frac{\textrm{det}\Omega ^{\prime }}{\textrm{det}\Omega },\quad \Omega =I+\Gamma ,\quad \Omega ^{\prime }=\left( \begin{array}{cc} 0 &{} \hat{G} \\ E &{} \Omega \\ \end{array} \right) . \end{aligned}$$
(27)

For example, when \(N=1\), Let \(\alpha _1\beta _1\ne {0}\), we obtain spatially localized and temporally periodic bound states [16]. The corresponding single-soliton solutions is displayed in fig.1(b).

Fig. 1
figure 1

Single-soliton solution for the Sasa–Satsuma equation: a \(\gamma _1=1+\textrm{i},\lambda _1=1\). b \(\alpha _1=\beta _1=1,k_1=0.5+\textrm{i}.\)

Full size image

3 Higher-Order Soliton Solutions for Sasa–Satsuma Equation

In this section we consider a soliton solution corresponding to a single multiple pole of arbitrary order, that is \(p_{l}\)-th order pole in the point \(k_{l}\). For the sake of simplicity, here we only consider the case \(k_l=i\lambda _{l}\) and take the spectral transform \(R_0\) in the form

$$\begin{aligned} R_0=\pi \sum ^{p_{l}}_{j=0}\left( \begin{array}{ccc} 0 &{} \gamma _{j}^{l}\omega ^{(j)}_{l+} &{} -(-1)^{j}\overline{{\gamma }_{j}^{l}}\omega ^{(j)}_{l+} \\ -\bar{\gamma }_{j}^{l}\omega ^{(j)}_{l-} &{} 0 &{} 0 \\ (-1)^{j}\gamma _{j}^{l}\omega ^{(j)}_{l-} &{} 0 &{} 0 \\ \end{array} \right) , \end{aligned}$$
(28)

where \(\omega ^{(j)}_{l\pm }=\delta ^{(j)}(k\mp \textrm{i}\lambda _l)\). Here the choice of spectral transform \(R_0\) is more general than [10].

As the process described in the Sect.2.3. Plugging (28) into (12) and by means of the formula [9]

$$\begin{aligned} \iint {d{\ell }}\wedge {d\bar{\ell }}f(l,\bar{l})\delta ^{(p)}(\ell -k)=(-1)^{p+1}2\textrm{i}\frac{\partial ^{p}{f(k,\bar{k})}}{\partial {k^{p}}}, \end{aligned}$$

we can obtain

$$\begin{aligned} q=-2\textrm{i}\tilde{G}\tilde{\Psi }_{11}^{T}, \end{aligned}$$
(29)

where \(\tilde{G}\) and \(\tilde{\Psi }_{11}\) are \((p_l+1)\)-dimensional row vector

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} \tilde{G} \\ \end{array} \right) _{1n}&=\sum ^{p_{l}}_{j=n-1}(-1)^{j+1}C^{n-1}_{j}\frac{\partial ^{(j-n+1)}\tilde{g}_{j}}{\partial {\ell ^{(j-n+1)}}}|_{\ell =\textrm{i}\lambda _{l}},\quad \tilde{g}_{j}=\gamma ^{l}_je^{-2i(\ell {x}+4\ell ^3{t})}, \\ \tilde{\Psi }_{11}&=\left( \begin{array}{ccccc} \psi _{11}(\textrm{i}\lambda _{l}) &{} \cdots &{} \frac{\partial ^{(n-1)}{\psi _{11}}}{\partial {\ell ^{(n-1)}}}|_{\ell =\textrm{i}\lambda _{l}} &{} \cdots &{} \frac{\partial ^{(p_l)}{\psi _{11}}}{\partial {\ell ^{p_l}}}|_{\ell =\textrm{i}\lambda _{l}} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

Substituting the explicit form of R(k) (25) into the equation in the integral form (8), we derive a linear algebraic system

$$\begin{aligned} (I+\Gamma )\tilde{\Psi }_{11}^{T}=\tilde{E}, \end{aligned}$$
(30)

where

$$\begin{aligned} \begin{aligned} \tilde{E}&=\left( \begin{array}{cccccc} 1 &{} 0 &{} \cdots &{} 0 &{} \cdots &{} 0 \\ \end{array} \right) ,\qquad \Gamma =\bar{\Gamma }_1\Gamma _1+\Gamma _2\bar{\Gamma }_2,\\ (\Gamma _1)_{mn}&=\sum ^{p_{l}}_{j=n-1}(-1)^{j+1}C^{n-1}_{j}\frac{\partial ^{(j-n+m)}(\frac{\tilde{g}_{j}}{\ell -k})}{\partial {\ell ^{(j-n+1)}}\partial {k^{(m-1)}}}|_{\ell =\textrm{i}\lambda _{l},k=-\textrm{i}\lambda _{l}},\\ (\Gamma _2)_{mn}&=-\sum ^{p_{l}}_{j=n-1}C^{m-1}_{j}\frac{\partial ^{(j-n+m)}(\frac{\tilde{g}_{j}}{\ell -k})}{\partial {\ell ^{(j-n+1)}}\partial {k^{(m-1)}}}|_{\ell =-\textrm{i}\lambda _{l},k=\textrm{i}\lambda _{l}}. \end{aligned} \end{aligned}$$

From (29) and (30), by calculation we can obtain the determinant form for \(p_l\)-th order soliton solution in the point \(k_l\)

$$\begin{aligned} q=-2\textrm{i}\frac{\textrm{det}\tilde{\Omega }^{\prime }}{\textrm{det}\tilde{\Omega }},\quad \tilde{\Omega }=I+\Gamma ,\quad \tilde{\Omega }^{\prime }=\left( \begin{array}{cc} 0 &{} \tilde{G}\\ \tilde{E} &{} \tilde{\Omega } \\ \end{array} \right) . \end{aligned}$$
(31)

Example 1

(The second and third order solution) Assuming \(p_{l}=1\), i.e. the spectral transform

$$\begin{aligned} R_0=\pi \left( \begin{array}{ccc} 0 &{} \gamma _{0}^{l}\omega _{l+}+\gamma _{1}^{l}\omega ^{(1)}_{l+} &{} -\gamma _{0}^{l}\omega _{+}+\gamma _{1}^{l}\omega ^{(1)}_{+} \\ -\gamma _{0}^{l}\omega _{l-}-\gamma _{1}^{l}\omega ^{(1)}_{l-} &{} 0 &{} 0 \\ \gamma _{0}^{l}\omega _{l-}-\gamma _{1}^{l}\omega ^{(1)}_{l-} &{} 0 &{} 0 \\ \end{array} \right) \end{aligned}$$

and taking account of the formulas (31), the expression for a second order soliton solution in the point \(\lambda _{l}\) can be obtained and is displayed in Fig. 2. Here

$$\begin{aligned} \begin{aligned} \Gamma _1&=\left( \begin{array}{cc} -(\frac{\gamma ^{l}_{0}+2\textrm{i}\gamma ^{l}_{1}(x-12\lambda ^{2}_{l}t)}{ 2\textrm{i}\lambda _{l}}+\frac{\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^2})e^{2\theta _l}&{} \frac{\gamma ^{l}_{1}}{2\textrm{i}\lambda _{l}}e^{2\theta _l} \\ -(\frac{\gamma ^{l}_{0}+2\textrm{i}\gamma ^{l}_{1}(x-12\lambda ^{2}_{l}t)}{ (2\textrm{i}\lambda _{l})^2}+\frac{2\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^3})e^{2\theta _l}&{} \frac{\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^2}e^{2\theta _l} \\ \end{array} \right) ,\\ \Gamma _2&=\left( \begin{array}{cc} (\frac{\gamma ^{l}_{0}+2\textrm{i}\gamma ^{l}_{1}(x-12\lambda ^{2}_{l}t)}{ 2\textrm{i}\lambda _{l}}+\frac{\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^2})e^{2\theta _l}&{} \frac{\gamma ^{l}_{1}}{2\textrm{i}\lambda _{l}}e^{2\theta _l} \\ -(\frac{\gamma ^{l}_{0}+2\textrm{i}\gamma ^{l}_{1}(x-12\lambda ^{2}_{l}t)}{ (2\textrm{i}\lambda _{l})^2}+\frac{2\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^3})e^{2\theta _l}&{} -\frac{\gamma ^{l}_{1}}{(2\textrm{i}\lambda _{l})^2}e^{2\theta _l} \\ \end{array} \right) ,\\ \tilde{E}&=\left( \begin{array}{cc} 1 &{} 0 \\ \end{array} \right) ^{T},\quad \tilde{G}=\left( \begin{array}{cc} -[\gamma ^{l}_{0}+2\textrm{i}\gamma ^{l}_{1}(x-12\lambda ^{2}_{l}t)]e^{2\theta _l} &{} \gamma ^{l}_{1}e^{2\theta _l} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

When \(p_{l}=2\), from (31) the corresponding third order soliton solution is plotted in Fig. 3.

Fig. 2
figure 2

Double pole soliton solution for the Sasa–Satsuma equation with \(\gamma ^{l}_0=1,\gamma ^{l}_1=\textrm{i},k_{l}=\textrm{i}\). a The 3-D structure; b the density structure

Full size image
Fig. 3
figure 3

Triple pole soliton solution for the Sasa–Satsuma equation with \(\gamma ^{l}_0=1,\gamma ^{l}_1=\textrm{i},\gamma ^{l}_2=1, k_{l}=\textrm{i}\). a The 3-D structure; b the density structure

Full size image

Remark

If we consider N distinct poles \(k_1,k_2,\ldots ,k_{l},\ldots ,k_N\) and their order are \(p_1, p_2,\ldots ,p_{l}, \ldots ,p_N\) respectively, the spectral transform can be taked in the following form

$$\begin{aligned} R_0=\pi \sum ^{N}_{l=1}\sum ^{p_{l}}_{j=0}\left( \begin{array}{ccc} 0 &{} \gamma _{j}^{l}\omega ^{(j)}_{+} &{} -(-1)^{j}\bar{\gamma }_{j}^{l}\omega ^{(j)}_{+} \\ -\bar{\gamma }_{j}^{l}\omega ^{(j)}_{-} &{} 0 &{} 0 \\ (-1)^{j}\gamma _{j}^{l}\omega ^{(j)}_{-} &{} 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$
(32)

As the process described in above, we can drive the expression for the general multiple pole solutions similar to the formulas (31). To illustrate, we give an example of the interaction between one simple pole soliton and the other one double pole soliton.

Example 2

(The interaction between one simple pole and the other one double pole) Let us choose \(k_1=\textrm{i}\lambda _1, p_{1}=1, k_2=\textrm{i}\lambda _2, p_{2}=0\), and then the spectral transform (32) in the form

$$\begin{aligned} R_0=\pi \left( \begin{array}{ccc} 0 &{} \tilde{\omega }_{+}+\gamma _{1}^{1}\omega ^{(1)}_{1+} &{} -\tilde{\omega }_{+}+\gamma _{1}^{1}\omega ^{(1)}_{1+} \\ -\tilde{\omega }_{-}-\gamma _{1}^{1}\omega ^{(1)}_{1-} &{} 0 &{} 0 \\ \tilde{\omega }_{-}-\gamma _{1}^{1}\omega ^{(1)}_{1-} &{} 0 &{} 0 \\ \end{array} \right) \end{aligned}$$
(33)

where \(\tilde{\omega }_{\pm }=\gamma _{0}^{1}\omega _{1\mp }+\gamma _{0}^{2}\omega _{2\mp }\). As the process described in above, we can obtain the expression (31) for a soliton solution related to one simple pole and the other one double pole, where

$$\begin{aligned} \begin{aligned}&\Gamma _1=\left( \begin{array}{ccc} -(\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ 2\textrm{i}\lambda _{1}}+\frac{\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^2})e^{2\theta _1}&{} \frac{\gamma ^{1}_{1}}{2\textrm{i}\lambda _{1}}e^{2\theta _1}&{} -\frac{\gamma ^{2}_{0}}{\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2}}e^{2\theta _2} \\ -(\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ (2\textrm{i}\lambda _{1})^2}+\frac{2\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^3})e^{2\theta _1}&{} \frac{\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^2}e^{2\theta _1}&{} -\frac{\gamma ^{2}_{0}}{(\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2})^2}e^{2\theta _2} \\ -(\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ \textrm{i}\lambda _{1}+\textrm{i}\lambda _{2}}+\frac{\gamma ^{1}_{1}}{(\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2})^2})e^{2\theta _1}&{} \frac{\gamma ^{1}_{1}}{\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2}}e^{2\theta _1}&{} -\frac{\gamma ^{2}_{0}}{2\textrm{i}\lambda _{2}}e^{2\theta _2} \end{array} \right) ,\\&\Gamma _2=\left( \begin{array}{ccc} (\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ 2\textrm{i}\lambda _{1}}+\frac{\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^2})e^{2\theta _1}&{} \frac{\gamma ^{1}_{1}}{2\textrm{i}\lambda _{1}}e^{2\theta _1}&{} \frac{\gamma ^{2}_{0}}{\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2}}e^{2\theta _2} \\ -(\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ (2\textrm{i}\lambda _{1})^2}+\frac{2\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^3})e^{2\theta _1}&{} -\frac{\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^2}e^{2\theta _1} &{} -\frac{\gamma ^{2}_{0}}{(\textrm{i}\lambda _{1}+\textrm{i}\lambda _{2})^2}e^{2\theta _2}\\ (\frac{\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{1}t)}{ 2\textrm{i}\lambda _{1}}+\frac{\gamma ^{1}_{1}}{(2\textrm{i}\lambda _{1})^2})e^{2\theta _1}&{} \frac{\gamma ^{1}_{1}}{2\textrm{i}\lambda _{1}}e^{2\theta _1}&{} \frac{\gamma ^{2}_{0}}{2\textrm{i}\lambda _{2}}e^{2\theta _2} \end{array} \right) ,\\&\tilde{E}=\left( \begin{array}{ccc} 1 &{} 0 &{} 1\\ \end{array} \right) ^{T},\quad \tilde{G}=\left( \begin{array}{ccc} -[\gamma ^{1}_{0}+2\textrm{i}\gamma ^{1}_{1}(x-12\lambda ^{2}_{l}t)]e^{2\theta _l} &{} \gamma ^{1}_{1}e^{2\theta _l}&{}-\gamma ^{2}_{0}e^{2\theta _l} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

The interaction is shown in Fig. 4.

Fig. 4
figure 4

The soliton solution related to one simple pole and one double pole for the Sasa–Satsuma equation with \(\gamma ^{l}_0=1,\gamma ^{l}_1=\textrm{i},\gamma ^{l}_2=1, k_{l}=\textrm{i}, k_{2}=2\textrm{i}\). a The 3-D structure; b the density structure

Full size image

4 Conclusions and Discussions

We analyzed the process dealing with multiple pole soliton solutions for Sasa–Satsuma equation by means of \(\bar{\partial }\) method in detail. In the frame of \(\bar{\partial }\) problem it’s easy to derive the explicit determinant form of multiple pole solutions. It should be noted that other methods such as the inverse scattering scheme, generalized Darboux transform could be applied as well for multiple pole soliton solution, but the \(\bar{\partial }\) method leads directly to the final results. In this paper the potentials q(x) is considered under ZBC, we know that under nonzero boundary condition it is more complicated to solve double pole solutions by the inverse scattering transform based on Riemann–Hilbert method in the literature [14]. So we will take advantage of this method to the NZBC case in the near future.