1 Introduction

1.1 Induced Information Fusion and Induced Aggregation Operators

The general information fusion theory and techniques are of wide applicability and have been hot areas of research for decades [1,2,3,4,5,6]. Aggregation operators [4] serve as an important theoretical basis and strict paradigm for information fusion practices. With a vector of input values \(\mathbf{{x}} = ({x_i})_{i = 1}^n\), a real valued aggregation operator (otherwise known as aggregation function) is a function \(A:{[0,1]^n} \rightarrow [0,1]\) such that: (I) (monotonicities) \(A(\mathbf{{x}}) \le A(\mathbf{{y}})\) whenever \(\mathbf{{x}} < \mathbf{{y}}\) (i.e., \({x_i} \le {y_i}\) and \(\mathbf{{x}} \ne \mathbf{{y}}\)); (ii) (boundary conditions) \(A(\mathbf{{0}}) = 0\) and \(A(\mathbf{{1}}) = 1\) (\(\mathbf{{0}} = (0,\cdots ,0)\) and \(\mathbf{{1}} = (1,\cdots ,1)\)). Aggregation operators are particularly useful in multi-criteria decision-making (MCDM) and multi-agent evaluation problems [7].

Some aggregation operators do not involve any outside preference and consist in their only structural characteristics; this part mainly includes some logic operators such as t-norms, t-conorms, semi-copulas [5], and numerous various mean operators (without involving weight vectors or preferences). The other part of aggregation operators are attached with preferences (e.g., from decision makers) such as weighted mean, ordered weighted averaging (OWA) operators [8], induced ordered weighted averaging (IOWA) operators [9], Choquet integrals [3] and other fuzzy measure-based operators [7, 10].

In general, there are two categories of preferences: non-ordered and ordered (or bi-polar). The non-ordered preferences mainly refer to weight preference (e.g., in MCDM problems), whereas the ordered (or bi-polar) preferences are majorly related to OWA and IOWA aggregation. Note that fuzzy measure-based aggregation operators (e.g., Choquet integrals) will use fuzzy measures (or capacities) [3] as their involved preferences which can simultaneously embody both non-ordered and ordered preferences. For a successful and accurate method of merging these two categories of preferences into fuzzy measures, one may refer to [11].

Given a vector of inputs, non-ordered preference allocation mainly use some objective or subjective weighting techniques, whereas ordered preference allocation generates weights according to some inducing factors such as the magnitudes, certainty degrees, and chronological orders of the inputs. Recall that these inducing factors correspond to bi-polar preferences with different practical meanings: optimism–pessimism preference, certainty strong–neutral preference, and time-related future–present preference, respectively. Numerous OWA- and IOWA-related studies provide with variety of techniques to generate weights with inducing factors and inducing information [9, 12,13,14]. Put simply, if a bi-polar preference is over inputs with larger magnitudes (or earlier obtained), then we generally should assign more weights to those entries with larger magnitudes (or earlier obtained). In words, to comprehensively aggregate the given vector of uncertain information, we need a weight vector which is the embodiment or representation of the desired ordered preference or non-ordered preference.

As data can be aggregated, different preferences (and their corresponding weight vectors) can also be merged. On one hand, for non-ordered preferences, if they are with the same dimension, it is trivial to know that the convex combination of them is the most natural form. On the other hand, for different ordered preferences, since they may come from different practical meanings of inducing information such as magnitude order, certainty order, confidence order, and chronological order, the direct use of convex combination method apparently does not valid or reasonable. Nevertheless, with some special permutation-based technique [15], the aggregation operators and processes with ordered preferences formally can be reformulated as non-ordered ones, which enable the convex combination of several different ordered preferences (or convex form of both ordered and non-ordered preferences), significantly facilitating and increasing the flexibility of preferences merging.

This work focuses on bi-polar preferences involved aggregation operators and processes, although in some certain aggregation and decision stage we may also use a permutation-based technique to formally transform them into non-ordered ones.

1.2 Multi-source Induced Aggregation with Basic Uncertain Information

Instead of definite information, in practice uncertain information is ever-increasingly pervasive in numerous areas. Some well-known numerical uncertain information includes interval information, intuitionistic fuzzy information [16], vague information [17], and the recently proposed basic uncertain information (BUI) [18, 19]. Basic uncertain information can serve as an uncertainty paradigm to generalize several kinds of uncertain information. In recent years, the theory of BUI has been further developed and applied [20,21,22,23,24,25,26]. A BUI granule is expressed with a pair \((x,c) \in {[0,1]^2}\) in which c is the certainty degree of the main value x. Certainty degree can flexibly have various meanings. For instance, it may indicate the extent to which decision makers are confident, sure, certain or definite of the main values, whereas uncertainty degrees (\(1 - c\)) can show the extents to which they are unconfident, unsure, uncertain, or indefinite of the main values.

The aggregation for uncertain information is with significant importance and has been gradually studied during the past decades [7, 10, 27,28,29,30]. Be it as it may, the studies of bi-polar preference-based aggregations for uncertain information are still insufficient and far from systematic.

Recall that when performing OWA aggregation, we only consider the magnitude information of inputs as the sole inducing factor, and once involving another inducing factor such as chronological information of input, it becomes IOWA aggregation. However, most of uncertain information is with more complex forms. For example, a vector of interval information granules take the form \(([{a_i},{b_i}])_{i = 1}^n\) which may contain different kinds of inducing information including \(({a_i})\), \(({b_i})\), \(({a_i}{b_i})\), \((\lambda {a_i} + (1 - \lambda ){b_i})\) and so on. Similarly, intuitionistic fuzzy information and vague information also contain several inducing factors since they are with the same mathematical structure as interval information though with differing practical meanings. Literature [12] discussed some convex combination methods to consider all the inducing factors and merge their respectively derived weight vectors to generate a final single weight vector embodying all factors. However, the method to derive the special weights to carry out the combination in BUI environment is not discussed.

With a vector of BUI granules \((({x_i},{c_i}))_{i = 1}^n\), there also may have several inducing factors such as \(({x_i})\), \(({c_i})\), \(({x_i}{c_i})\), \((\min ({x_i},{c_i}))\) and so on. Therefore, ordered preferences can be based on any one of the mentioned inducing factors. Recently, some literatures consider and include the situation where no such bi-polar preference can be obtained [22, 31]. Besides, those literatures discuss and propose some methods to derive the special weights to carry out the combination of the weight vectors generated, respectively, from different inducing factors. However, the limitations therein are also clear. It points out that when different factors of preferences are obtained from a single expert, sometimes some subtle cognitive inconsistency may occur [31]. Although such cognitive inconsistency can be removed or ameliorated, actually some key information for determining the special weights to carry out the combination may not always be obtained from a same group of experts. That is, when the special weights (to carry out the combination) cannot be obtained or elicited from experts who are requested to provide some of the information about bi-polar preference extents, the combination method to merge different preferences (and their derived weight vectors) cannot work.

To address the above problem, this work will propose some auto-generation methods to obtain relative importance between each inducing factor and hence to perform the required convex combination form. These methods only need experts to provide with some certain types of information about the bi-polar preference extents for different inducing factors from which the relative importance between all inducing factors will be automatically derived in some reasonable and workable way. Under the same decision environment involving multiple experts, we consider three different ways to elicit some initial information provided by experts, from which we further derive out the two parts of key information, bi-polar preference extents and relative information for inducing factors to determine a final weight vector for performing comprehensive evaluation over given vector of BUI granules.

The remainder of this work is organized as follows. Section  2 reviews some necessary knowledge and fixes some notations. In Sect. 3, some methodologies for preference and uncertainty involved information fusion are discussed as the basis and rational for the later proposed evaluation procedures. Section 4 discusses three methods, statistic method, distance method and linguistic variable method, to derive relative importance between different inducing factors. Section 5 elaborates on the whole evaluation procedure. A numerical example is presented in Sect. 6. Section 7 concludes and remarks this work.

2 Preparations

This section reviews some necessary knowledge mainly about BUI and OWA aggregation, and fixes some notations for use throughout this work.

Definition 1

[18, 19] A BUI granule is with a pair (x, c) in which \(x \in [0,1]\) is a main value and \(c \in [0,1]\) the associated certainty degree to x. \(1 - c \in [0,1]\) is the associated uncertain degree of x.

Remark

The BUI granule (x, 1) practically degenerates into the real number x because its full certainty is achieved for the main value x; conversely, the BUI granule (x, 0) tells the full uncertainty is reached for the main value x, and thus no substantial information is available for use.

\(\mathbf{{x}} = ({x_i})_{i = 1}^n \in {[0,1]^n}\) denotes a real valued vector of dimension n. The set of all BUI granules (x, c) is denoted by \({{\mathcal {B}}}\). A BUI vector is denoted by \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^n \in {{{\mathcal {B}}}^n}\), where \(\mathbf{{x}} = ({x_i})_{i = 1}^n \in {[0,1]^n}\) is a main vector and \(\mathbf{{c}} = ({c_i})_{i = 1}^n \in {[0,1]^n}\) is the certainty vector associated with x. A (normalized) weight vector (of dimension n) is with the form \(\mathbf{{w}} = ({w_i})_{i = 1}^n \in {[0,1]^n}\) (\(\sum \nolimits _{i = 1}^n {{w_i}} = 1\)), and the space of all such weight vectors of dimension n is denoted by \({{{\mathcal {W}}}^{(n)}}\).

The weighted arithmetic mean for a vector of real values and BUI granules take the following modalities, respectively.

Definition 2

The weighted arithmetic mean (with weight vector w) (WAM) is defined with

$$\begin{aligned} {{\mathsf{{WAM}}_\mathbf{{w}}}(\mathbf{{x}}) = \sum \limits _{i = 1}^n {{w_i}{x_i}}}. \end{aligned}$$
(1)

Definition 3

[18] The BUI weighted arithmetic mean (with weight vector w) (BWAM) \(\mathsf{{BWAM}}{_\mathbf{{w}}}:{{{\mathcal {B}}}^n} \rightarrow {{\mathcal {B}}}\) is defined with

$$\begin{aligned} {\mathsf{{BWAM}}{_\mathbf{{w}}}(\mathbf{{x}},\mathbf{{c}}) = \left( {\sum \limits _{i = 1}^n {{w_i}{x_i}} ,\sum \limits _{i = 1}^n {{w_i}{c_i}} } \right) }. \end{aligned}$$
(2)

The well-known OWA operator is introduced by Yager and its original definition is below.

Definition 4

[8] (OWA operator) An OWA operator (of dimension n) with weight vector w is a mapping \({\mathsf{{OWA}}_\mathbf{{w}}}:{[0,1]^n} \rightarrow [0,1]\) such that

$$\begin{aligned} {\mathsf{{OWA}}{_\mathbf{{w}}}(\mathbf{{x}}) = \sum \limits _{i = 1}^n {{w_i}{x_{\sigma (i)}}}}, \end{aligned}$$
(3)

where \(\sigma :\{ 1,\ldots ,n\} \rightarrow \{ 1,\ldots ,n\}\) is any suitable permutation on \(\{ 1,\ldots ,n\}\) such that \({x_{\sigma (i)}} \ge {x_{\sigma (j)}}\) whenever \(i < j\).

Yager also used orness/andness to numerically express the extent of optimism–pessimism preference contained in w. Note that orness/andness can be also flexibly used to indicate the extents of preferences from other inducing factors.

Definition 5

[8] The orness/andness of any weight vector w (applied in OWA aggregation) is defined as follows

$$\begin{aligned} orness\,(\mathbf{{w}}) & = \sum \limits _{i = 1}^n {\frac{{n - i}}{{n - 1}}{w_i}}, \end{aligned}$$
(4)
$$\begin{aligned} andness\,(\mathbf{{w}}) & = \sum \limits _{i = 1}^n {\frac{{i - 1}}{{n - 1}}{w_i}} = 1 - orness\,(\mathbf{{w}}). \end{aligned}$$
(5)

In this work, we do not discuss the formal definition of IOWA operators or IOWA aggregations for the reason that both OWA and IOWA aggregation can be equivalently expressed as WAM aggregation with some transformed weighted using some special techniques [15]. Recall that in Yager’s original definitions for IOWA, a vector of inputs consists of several pairs (like BUI granules) \(({x_i};{t_i})_{i = 1}^n\) in which \(({x_i})_{i = 1}^n\) is the mainly concerned value for evaluating and assessing, and \(({t_i})_{i = 1}^n\) is called an inducing vector or inducing variable (information or factor). It is inducing variable that determine the weight allocation when a weight vector \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) is obtained, which can be regarded as “ordered” to differentiate from a usual weight vector that is not related to ordered preference. Put simply, in IOWA-related weights allocation process, the weights in w with lower subscripts will be assigned to the pairs \(({x_i};{t_i})\) that have bigger or smaller \({t_i}\). For more specific weights allocation techniques related to OWA and IOWA aggregation, refers to [6, 32,33,34].

3 Some Methodologies for Preference and Uncertainty Involved Information Fusion

3.1 Bi-polar Preferences Over Given Vector of Real Values

In WAM and formula (1), given a vector of real values, another prerequisite is a certain weight vector which actually can be derived from different means or have various meanings. For example, the vector w can be derived from some mathematical optimization method with certain application backgrounds, from subjective opinions, from statistics or even directly from a mere identical discrete probability vector. The preferences derived from above mentioned methods can be subsumed into non-ordered preference. In WAM and formula (1), we can recognize that the “values” have taken their position in order of natural numbers prior to the “weights” positioning process; then, each determined weight is inserted into a suitable position corresponding to an existing value.

In contrast, Yager proposed the OWA (IOWA) aggregation and the weights determination mechanism which are based on ordered preferences or bi-polar preferences. Apart from the existing differences in practical meanings and backgrounds, the major formative difference lies in that OWA (IOWA) weights determination method firstly determine a weight vector only according to a given preference degree (say, orness/andness), irrespective of the involved multiple agents or criteria. Then, with the determined weight vector, the OWA aggregation in (3) is practically a weight-value coordinating process in which “value” should be inserted into the suitable position where the“weight” have already taken position in order of natural numbers in advance.

Put simply, the weight vector \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) used to perform OWA aggregation is “ordere” and thus, to avoid spoiling such “orde” (which entails that larger values in \(\mathbf{{x}} = ({x_i})_{i = 1}^n\) correspond to the weights entries in the front positions of \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) with lower subscripts), we have to reorder the value vector \(\mathbf{{x}} = ({x_i})_{i = 1}^n\) into the form \(\mathbf{{x'}} = ({x'_i})_{i = 1}^n = ({x_{\sigma (i)}})_{i = 1}^n\) whose entries with smaller subscripts just correspond to the weights entries with lower subscripts. In this sense, the value vector x can be seen as somewhat “passive” because the weight vector has been determined beforehand and the reordering of x will be done afterwards.

Orness/andness can be applied to measure the bi-polar preference strength. Usually, there are two preference modes: for the first one, larger orness values correspond to larger preference strengths, and smaller orness values to smaller preference strengths; for the second one, larger and smaller orness values correspond to larger preference strengths, and the orness values near 0.5 correspond to smaller preference strength. For example, when modeling optimism, we use the first mode; and when modeling the certainty strong–neutral preference, we may use a half range of orness values and the second preference mode usually applies well.

Given any weight vector w (used in OWA or IOWA aggregation), its orness/andness is unique. However, the converse is apparently not true. For example, suppose given a orness value \(\alpha = 0.5\), with dimension 4 we have \(\mathbf{{a}} = (0.25,0.25,0.25,0.25)\) and \(\mathbf{{h}} = (0.5,0,0,0.5)\), and then observe \(orness(\mathbf{{a}}) = orness(\mathbf{{h}}) = 0.5\) but \(\mathbf{{a}} \ne \mathbf{{h}}\). Notwithstanding several developed methods to generate weight vectors for OWA aggregation with given orness values, it is more convenient to use parameterized family of weight vectors. Recall for two weight vectors \({\mathbf{{w}}_1},{\mathbf{{w}}_2} \in {{{\mathcal {W}}}^{(n)}}\), we say \({\mathbf{{w}}_1} \le {\mathbf{{w}}_2}\) if and only if \(\sum \nolimits _{k = 1}^i {{w_{1k}}} \le \sum \nolimits _{k = 1}^i {{w_{2k}}}\) for all \(i \in \{ 1,\cdots ,n\}\) (we speak of \({\mathbf{{w}}_1} < {\mathbf{{w}}_2}\) if \({\mathbf{{w}}_1} \le {\mathbf{{w}}_2}\) and \({\mathbf{{w}}_1} \ne {\mathbf{{w}}_2}\)) [35]. It can be observed that for any two weight vectors \({\mathbf{{w}}_1},{\mathbf{{w}}_2} \in {{{\mathcal {W}}}^{(n)}}\), if \({\mathbf{{w}}_1} \le {\mathbf{{w}}_2}\) then \(orness({\mathbf{{w}}_1}) \le orness({\mathbf{{w}}_2})\), whereas the reverse proposal does not hold. Nevertheless, recall that a (parameterized) family of weight vectors (in OWA/IOWA aggregation) \({\{ {\mathbf{{w}}^{ < \alpha > }}\} _{\alpha \in [0,1]}}\) [36] satisfies (I) \({\mathbf{{w}}^{< {\alpha _1}> }}< {\mathbf{{w}}^{ < {\alpha _2} > }}\) whenever \({\alpha _1} < {\alpha _2}\); (II) \(orness({\mathbf{{w}}^{ < \alpha > }}) = \alpha\) for all \(\alpha \in [0,1]\). The forgoing definition immediately implies that in practice using a certain family of weight vector guarantees both the differentiation and comparison of any two weight vectors whose orness values are distinct.

It deserves to emphasize that with a given weight vector \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) (whose subscripts are in the order of natural numbers), if it is for OWA aggregation (or related weights allocation), then the weights with lower subscripts will correspond to the values with higher magnitudes, but if it is for IOWA aggregation (or related weights allocation), then the weights with lower subscripts will correspond to the values with the attached inducing variables that are bigger or smaller.

In this work, we mainly concern the two bi-polar preferences: optimism–pessimism preference and certainty strong–neutral preference. The meaning for the first preference is clear; it refers to whether some decision maker prefers big input values or small input values. The related orness range is [0, 1] in which the maximum value 1 corresponds solely to the extreme optimism and the weight vector \({\mathbf{{w}}^*} = (1,\cdots ,0)\), and the minimum value 0 corresponds solely to the extreme pessimism and the weight vector \({\mathbf{{w}}_*} = (0,\cdots ,1)\). For any other orness value \(\alpha \in [0,1]\), if \(\alpha > 0.5\), it is related to an optimistic attitude while if \(\alpha < 0.5\), it is related to a pessimistic attitude. As for the second preference, it is aimed for the inducing variable of certainty degrees in a vector of BUI granules. Note that in practice decision makers usually will not attach higher importance to those granules with lower certainties, then an orness range of [0.5, 1] is sufficient and reasonable; and the larger the orness, the more weights will be assigned to those granules with higher certainties and in this case orness 0.5 corresponds to the sole weight vector \(\mathbf{{a}} = (1/n,\cdots ,1/n)\) and neutral attitude.

Note that with an obtained weight vector, we need not practically perform the OWA or IOWA aggregation with it. In this work, with obtaining such a weight, we only use it to carry out the corresponding weights allocation process, as we will see later, because the input vector of granules is of BUI wherein several inducing factors/variables exist and thus, a single weight vector cannot be directly and sufficiently applied to aggregate the input vector.

3.2 Merging Ordered and Non-ordered Preference

In formula (1), the involved weight vector w can be of any type. That is, the weight vector can be derived either from a single ordered preference (bi-polar preference) or from a single non-ordered preference. Moreover, the weight vector can also assume some merged form by merging several ordered or non-ordered preferences. Note that, however, once there is at least one ordered preference involved, then some permutation-based techniques should be applied to first re-transform into a consistent form in line with the order of the entries in the input vector. To clarify, within formula (3) we note that the weight vector \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) is derived from an ordered preference; when we want to merge it with another weight vector \(\mathbf{{v}} = ({v_i})_{i = 1}^n\) used in weighted arithmetic mean, some ordering inconsistency arise. This is because in (3), the \(i\mathrm{{th}}\) position corresponds to \({x_{\sigma (i)}}\), while in (1), the \(i\mathrm{{th}}\) position corresponds to \({x_i}\), and thus w and v cannot be merged directly unless after some permutation they all pertain to the same situation where the \(i\mathrm{{th}}\) position corresponds to \({x_i}\). To achieve this, we observe that in (3), there is an equivalent expression \({\mathsf{{OWA}}_\mathbf{{w}}}(\mathbf{{x}}) = \sum \nolimits _{i = 1}^n {{w_i}{x_{\sigma (i)}}} = \sum \nolimits _{i = 1}^n {{w_{{\sigma ^{ - 1}}(i)}}{x_i}} = W{A_{\mathbf{{w'}}}}(\mathbf{{x}})\), where \(\mathbf{{w'}} = ({w'_i})_{i = 1}^n = ({w_{{\sigma ^{ - 1}}(i)}})_{i = 1}^n\). Therefore, we can replace \(\mathbf{{w'}}\) with w and merge it with v to have the desired merged convex combination form \(\lambda \mathbf{{w'}} + (1 - \lambda )\mathbf{{v}}\), which is consistent because \(\mathbf{{w'}}\) and v are commensurable in sense that they both correspond to the same modality of weighted arithmetic mean where the \(i\mathrm{{th}}\) position corresponds to \({x_i}\).

Similarly, when we want to merge two weight vectors, \(\mathbf{{w}} = ({w_i})_{i = 1}^n\) and \(\mathbf{{v}} = ({v_i})_{i = 1}^n\), both from ordered preference and used in (3), the involved permutation \({\sigma _\mathbf{{w}}}\) (for w) and \({\sigma _\mathbf{{v}}}\) (for v) are different and in generally inconsistent in sense that their \(i\mathrm{{th}}\) positions correspond to \({x_{{\sigma _\mathbf{{w}}}(i)}}\) and \({x_{{\sigma _\mathbf{{v}}}(i)}}\) which may be with different subscripts. Therefore, we may still first obtain two intermediate weight vectors from w and v, namely, \(\mathbf{{w'}} = ({w'_i})_{i = 1}^n = ({w_{{\sigma _\mathbf{{w}}}^{ - 1}(i)}})_{i = 1}^n\) and \(\mathbf{{v'}} = ({v'_i})_{i = 1}^n = ({v_{{\sigma _\mathbf{{v}}}^{ - 1}(i)}})_{i = 1}^n\), and then take convex combination form of them by \(\lambda \mathbf{{w'}} + (1 - \lambda )\mathbf{{v'}}\).

4 Eliciting Initial Preference Information in Three Different Ways of Inquiry and Deriving Workable Weight Vectors

To derive relative importance between different inducing factors, this Section discusses three methods, statistic method, distance method and linguistic variable method from the mere bi-polar preference extents offered by decision makers. Each of them has advantages and disadvantages, and the third method serves as a trade-off between the first two methods. To show the establishment process of each method, we expound the ideas of them in turn, as well as the corresponding advantages and disadvantages, and summarize the relative feasibility and effectiveness of the language variable method.

4.1 Statistic Method to Derive Relative Importance Between Different Inducing Factors

We first briefly outline some schematic evaluation process in the triple environment of multi-experts, subjective preferences and BUI. In literature [22], some questionnaire based method is used to elicit original information from experts to further carry out the weights determination procedure in that complex environment. With the input for aggregation being a vector of BUI granules \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^n\), a panel of experts are inquired and requested to answer the following three questions as rephrased in what follows:

figure a

However, literature [31] pointed out that requesting individual expert to simultaneously answer Questions 1, 2 and 3 may cause some cognitive inconsistency in certain semantics. In actual, apart from this downside, in practice very frequently some experts even are not willing or unable to answer Question 3, while it is generally much easier for them to answer Question 1 and 2, due to the relative difficulty in answering Question 3.

Therefore, it is appealing that there are some methods that can only request experts to answer Questions 1 and 2 from which the information that would have been known from Question 3 can be automatically derived.

This subsection discusses a method using simple statistics. As presented in [31], we still assume M experts are inquired and each of them is with equal importance. Suppose for question 1 there are \({s_O}\), \({s_P}\) and \({s_N}\) experts (\({s_O} + {s_P} + {s_N} = M\)) who select “optimism”, “pessimism” and “neutral” preferences, respectively. Similarly, for question 2 assume there are \({t_S}\) and \({t_N}\) experts (\({t_S} + {t_N} = M\)) who select “strong” and “neutral” preferences, respectively.

Solely based on the above-elicited original information from experts as a whole, we can determine a normalized weight vector \(\mathbf{{q}} = ({q_{OP}},{q_{SN}},{q_N})\) to indicate the relative importance of “optimism–pessimism preference” (corresponding to \({q_{OP}}\)), “certainty strong–neutral preference” (corresponding to \({q_{SN}}\)), and “indifference” (corresponding to \({q_N}\)), respectively. Note that if an individual expert expresses “neutral” (attitude to the main input information \(({x_i})_{i = 1}^n\)), then he actually expressed the opinion of “indifference” to the bi-polar optimism–pessimism preference or of “none of the two preferences is important”. Hence, his opinion and vote should count for and contribute to “indifference” part to further form the weight vector q (i.e., corresponding to \({q_N}\)). If he expresses either “optimism” or “pessimism”, then this amounts to indicating that he thinks “optimism–pessimism” preference is concerned and important. Therefore, all the opinions and votes with these two preferences should constitute “optimism–pessimism” part to further form the weight vector q (i.e., corresponding to \({q_{OP}}\)). As for Question 2, if an expert expresses “neutral” preference, in a similar reasoning, his opinion and vote should also count for and contribute to “indifference” part (i.e., corresponding to \({q_N}\)). If he expresses “strong”, then this equals to indicating that he thinks “certainty strong–neutral” preference is concerned and important. Note that all the “votes” to “neutral” in both Question 1 and Question 2 will contribute to “none of them (indifference)” in the original Question 3, and thus \({s_N} + {t_N}\) constitutes the proportion of \({q_N}\). That is, any one expert actually has two “votes”, one for answering Question 1 and the other for Question 2, and having this in mind we can naturally have the following formula based on simple statistics.

$$\begin{aligned} {q_{OP}} & = \frac{{{s_O} + {s_P}}}{{2M}}, \end{aligned}$$
(6)
$$\begin{aligned} {q_{SN}} & = \frac{{{t_S}}}{{2M}}, \end{aligned}$$
(7)
$$\begin{aligned} {q_N} & = \frac{{{s_N} + {t_N}}}{{2M}}. \end{aligned}$$
(8)

Observe that \({q_{OP}} + {q_{SN}} + {q_N} = 1\).

The main advantage of this simple statistic method is that the invited experts can easily express their attitudes because there are only very few options for them to choose. The shortcoming of it, however, lies in that when the number of inquired experts is few, then the statistic result may not be convincing or even the inquiring process cannot actually workable.

The remaining task is to determine a desired numerical orness \(\alpha\) for optimism–pessimism preference from the answers of experts to Question 1, and determine a reasonable orness \(\beta\) to represent the preference strength for certainty strong–neutral preference from the answers of experts to Question 2. Still by simple statistic, we naturally have to use the following formulas.

$$\begin{aligned} {\alpha = \frac{{{s_O}}}{M} + 0.5\frac{{{s_N}}}{M}}, \end{aligned}$$
(9)
$$\begin{aligned} {\beta = \frac{{{t_S}}}{M}}. \end{aligned}$$
(10)

In (9), we actually give coefficient 1, 0.5 and 0 to \({s_O}\), \({s_N}\) and \({s_P}\) is because \(\alpha\) represents optimism extent and \({s_O}\) is the number of the experts who are “optimism”, \({s_P}\) is the number of the experts who are “pessimism” and \({s_N}\) is the number of the expert who are neither optimism nor pessimism and thus using the middle point between 1 and 0, i.e., 0.5, appears to be more appropriate.

4.2 Distance Method to Derive Relative Importance Between Different Inducing Factors

In some circumstance, the expert resource is limited and there may be only few or even one expert who is available to be inquired. Hence, some methods that can accommodate to such circumstance are important and practical. In such circumstance, we should replace the original Question 1 and Question 2 with the two new corresponding questions.

figure b

Suppose an individual expert could answer Questions 1 and 2, and can indicate that \(\alpha \in [0,1]\) is his optimism extent for Question 1 and \(\beta \in [0.5,1]\) is his expressed extent to which he prefer higher certainty degrees. Note that if \(\alpha = 1\) or \(\alpha = 0\), then it is clear that he fully shows “optimism” or “pessimism” (as in the original Question 1) which implies “optimism–pessimism” preference as needed to be answered for the original Question 3 (i.e., corresponding to \({q_{OP}}\)); if \(\alpha = 0.5\), then this “neutral” preference actually implies “indifference” (corresponding to \({q_N}\)). On the other hand, if \(\beta = 1\), then it is also clear that he fully shows “strong” preferences (as in the original Question 2) which implies “certainty strong–neutral” as for answering the original Question 3 (i.e., corresponding to \({q_N}\)); if \(\beta = 0.5\), then this “neutral” preference also implies “indifference” (corresponding to \({q_N}\)). When \(\alpha \in (0,0.5) \cup (0.5,1)\), then we can reasonably use the distance from it to 0.5 (i.e., \({d_1} = 2 \cdot \left| {\alpha - 0.5} \right|\) with normalization to unit) to indicate the preference extent of “optimism–pessimism” to original Question 3 (i.e., corresponding to \({q_{OP}}\)); similarly, if \(\beta \in (0.5,1)\), we can also reasonably use the distance from it to 0.5 (i.e., \({d_2} = 2 \cdot (\beta - 0.5)\) with normalization to unit) to indicate the preference extent of “certainty strong–neutral” to original Question 3 (i.e., corresponding to \({q_{SN}}\)). With above analysis, we have the following detailed formulas after some suitable normalization

$$\begin{aligned} {q_{OP}} & = \left| {\alpha - 0.5} \right| , \end{aligned}$$
(11)
$$\begin{aligned} {q_{SN}} & = \beta - 0.5, \end{aligned}$$
(12)
$$\begin{aligned} {q_N} & = 1 - {q_{OP}} - {q_{SN}}. \end{aligned}$$
(13)

The main advantage of this method is that it allows the situation where there is very few or even only one expert to answer questions to derive relative importance between different inducing factors. In this manner, with any individual expert, we can obtain \(\alpha\), \(\beta\) and \(\mathbf{{q}} = ({q_{OP}},{q_{SN}},{q_N})\) accordingly. When several experts are invited, we can take average form for these three types of information since they all allow combination and average forms.

4.3 Linguistic Variable Method to Derive Relative Importance Between Different Inducing Factors

The statistic method proposed in Sect. 4.1 requires any individual expert to choose from three options (for Question 1) and two options (for Question 2), respectively, and thus, this may be lacking in precision when there are relatively few experts invited. In contrast, the method presented in Sect. 4.2 requires any individual expert to choose from infinitely more options which belong to [0, 1] or [0.5, 1], which, though has fewer limiting on the number of experts invited, sometimes may be a harder choosing problem for experts. To balance the relative advantage and disadvantage as above, the use discrete linguistic variables that have finite linguistic scales is proposed, refer to [37].

We define that a symmetrical linguistic variable set with degree J (\(J \in \{ 1,2,\cdots \}\)) is expressed as an ordered set \(\{ {l_k}\} _{k = - J}^J\). For example, to be applied as a scale to measure “optimism–pessimism” preference, we can have \(\{ {l_k}\} _{k = - 3}^3\)= 3 very optimism, 2 optimism, 1 slightly optimism, 0 neutral, − 1 slightly pessimism, − 2 pessimism, − 3 very pessimism, or \(\{ {l_k}\} _{k = - 2}^2\)= 2 very optimism, 1 optimism, 0 neutral, − 1 pessimism, − 2 very pessimism. As another form, we define that a unilateral linguistic variable set with degree J (\(J \in \{ 1,2,\cdots \}\)) is expressed as an ordered set \(\{ {l_k}\} _{k = 0}^J\). For example, to serve as a suitable scale to measure “certainty strong–neutral” preference, we can have \(\{ {l_k}\} _{k = 0}^3\)= 3 very strong, 2 strong, 1 slightly strong, 0 neutral, or \(\{ {l_k}\} _{k = 0}^2\)= 2 very strong, 1 strong, 0 neutral. With such setting, we may select the two new questions to ask experts.

figure c

When an option (answer) is obtained by an ordered set \(\{ {l_k}\} _{k = - J}^J\), with a preset numerical scale for it, we can derive an orness degree closely related to \(\alpha\) by using a scale function, i.e., numerical optimism extent for Question 1. That is, a desired numerical scale can be a mapping \(H:\{ J,J - 1,\ldots ,0,\ldots , - J + 1, - J\} \rightarrow [0,1]\) such that (I) H is increasing; and (II) \(H(J) = 1\) and \(H( - J) = 0\). For example, when \(\{ {l_k}\} _{k = - 2}^2\) = 2 very optimism, 1 optimism, 0 neutral, − 1 pessimism, − 2 very pessimism, we may set a vector \(H = (1, 0.75, 0.5, 0.25, 0)\). When an option (answer) is obtained by an ordered set \(\{ {l_k}\} _{k = 0}^J\), with a preset numerical scale for it, we can derive an extent degree \(\beta\) to which he prefers higher certainty degrees, i.e., numerical extent degree for Question 2. That is, a pertinent numerical scale in this setting can be a mapping \({H^ + }:\{ J,J - 1,\ldots ,0\} \rightarrow [0, 1]\) such that (I) H is increasing; and (II) \(H(J) = 1\) and \(H(0) = 0.5\). For example, when \(\{ {l_k}\} _{k = 0}^3\)= 3 very strong, 2 strong, 1 slightly strong, 0 neutral, we may appropriately set a vector \({H^ + } = (1,0.8,0.6,0.5)\).

Subsequently, we analyze and derive relative importance between inducing factors in a similar manner to the distance method as discussed in the preceding subsection.

Assume an individual expert could answer Question 1 and 2, and can indicate that \(\alpha \in \{ {l_k}\} _{k = - 2}^2\) is his optimism extent choice for Question 1 and \(\beta \in \{ {l_k}\} _{k = 0}^3\) is his expressed extent choice to which he prefers higher certainty degrees. Note that if \(\alpha = \pm 2\) (i.e., “2 very optimism” or “− 2 very pessimism”), then it is clear that he fully shows “optimism” or “pessimism” (as in the original Question 1) which implies “optimism–pessimism” preference as needed to be answered for the original Question 3 (i.e., corresponding to \({q_{OP}}\)); if \(\alpha = 0\) (i.e., “0 neutral”), then this “neutral” preference actually implies “indifference” (corresponding to \({q_N}\)). On the other hand, if \(\beta = 3\) (i.e., “3 very strong”), then it is also clear that he fully shows “strong” preferences (as in the original Question 2) which implies “certainty strong–neutral” as for answering the original Question 3 (i.e., corresponding to \({q_{SN}}\)); if \(\beta = 0\) (i.e., “0 neutral”), then this “neutral” preference also implies “indifference” (corresponding to \({q_N}\)). When \(\alpha = \pm 1\), then we can reasonably use the distance from it to \(H(0) = 0.5\) (i.e., \({d_1} = 2 \cdot \left| {H(\alpha ) - H(0)} \right|\) with normalization to unit) to indicate the preference extent of “optimism–pessimism” to original Question 3 (i.e., corresponding to \({q_{OP}}\)); similarly, if \(\beta \in \{ 2,1\}\), we can also reasonably use the distance from it to \({H^ + }(0)\) (i.e., \({d_2} = 2 \cdot ({H^ + }(\beta ) - {H^ + }(0))\) with normalization to unit) to indicate the preference extent of “certainty strong–neutral” to original Question 3 (i.e., corresponding to \({q_{SN}}\)). With above analysis, we have the following detailed formulas after some suitable normalization

$$\begin{aligned} {q_{OP}} & = \left| {H(\alpha ) - H(0)} \right| , \end{aligned}$$
(14)
$$\begin{aligned} {q_{SN}} & = {H^ + }(\beta ) - {H^ + }(0), \end{aligned}$$
(15)
$$\begin{aligned} {q_N} & = 1 - {q_{OP}} - {q_{SN}}. \end{aligned}$$
(16)

4.4 Discussion of the Three Methods

These three methods have different advantages and disadvantages, shown in Table 1. The linguistic variable based method serves as a trade-off between the two methods proposed beforehand. When several experts are invited, we can take average form for these three types of information since there all allow combination and average forms. In the actual application process, one of the methods can be selected according to different situations.

Table 1 Comparison of the three methods
Full size table

5 The Complete Evaluation Process Encompassing the Forgoing Analyses

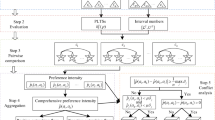
This section provides with a complete evaluation and decision-making procedure with bi-polar preferences involved aggregation in BUI and multi-agent environments in a systematic way. The whole evaluation process chooses to use linguistic variable method as presented in Sect. 4.3 and contains some main stages, each of which may have several sub-steps.


Stage I Information, preference collection and preparation

Step 1.1 Collect a vector of n BUI granules \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^n \in {{{\mathcal {B}}}^n}\).

Step 1.2 Invite a group of M experts and request them to merely provide the two questions as put in Sect. 4.3.

Step 1.3 Require each expert j (\(j = 1,\cdots ,M\)) to give an answer \({\alpha _j}\) from linguistic variable set \(\{ {l_k}\} _{k = - 2}^2\) = 2 very optimism, 1 optimism, 0 neutral, – 1 pessimism, – 2 very pessimism.

Step 1.4 Require each expert j (\(j = 1,\cdots ,M\)) to give an answer \({\beta _j}\) from linguistic variable set \(\{ {l_k}\} _{k = 0}^3\) = 3 very strong, 2 strong, 1 slightly strong, 0 neutral.


Stage II Preference elicitation, orness derivation and the determination of relative importance between inducing factors and indifference factor

Step 2.1 For each expert j (\(j = 1,\cdots ,M\)), obtain orness \(H({\alpha _j})\) for his optimism–pessimism preference. Take the average of \(H({\alpha _j})\) to obtain \(H(\alpha ) = \frac{1}{M}\sum \nolimits _{j = 1}^M {H({\alpha _j})}\).

Step 2.2 For each expert j (\(j = 1,\cdots ,M\)), obtain orness \({H^ + }(\beta )\) to represent his preference strength for certainty strong–neutral preference. Take the average of \({H^ + }({\beta _j})\) to obtain \({H^ + }(\beta ) = \frac{1}{M}\sum \nolimits _{j = 1}^M {{H^ + }({\beta _j})}\).

Step 2.3 For each expert j (\(j = 1,\cdots ,M\)), from (14), (15) and (16), respectively, to derive a normalized weight vector \({\mathbf{{q}}_j} = ({q_{j\_OP}},{q_{j\_SN}},{q_{j\_N}})\) to indicate, from his perspective, the relative importance of “optimism–pessimism preference”, “certainty strong–neutral preference”, and “indifference”, respectively. Take the average of \({\mathbf{{q}}_j}\) to obtain \(\mathbf{{q}} = \frac{1}{M}\sum \nolimits _{j = 1}^M {{\mathbf{{q}}_j}}\).


Stage III Weight vector obtaining and permuting

Step 3.1 Using the obtained \(\alpha\) and \(\beta\), immediately obtain the three weight vectors \({\mathbf{{r}}^{ < H(\alpha ) > }}\), \({\mathbf{{r}}^{ < {H^ + }(\beta ) > }}\) and a, where \({\mathbf{{r}}^{ < H(\alpha ) > }}\) is from a certain (parameterized) family of vectors \({\{ {\mathbf{{r}}^{ < \alpha > }}\} _{\alpha \in [0,1]}}\), \({\mathbf{{r}}^{ < {H^ + }(\beta ) > }}\) is also from the half of this family of vectors \({\{ {\mathbf{{r}}^{ < \beta > }}\} _{\beta \in [0.5,1]}}\), and \({\mathbf{{r}}^{ < 0.5 > }} = \mathbf{{a}} = (1/n)_{i = 1}^n\). This is because it is reasonable for “indifference” of expert to correspond to a with Laplace decision criterion. For more detailed explanations, refer to literature [22].

Step 3.2 As analyzed in Sect. 3.2, with the obtained \({\mathbf{{r}}^{ < H(\alpha ) > }}\), we should permute it into a new permuted vector \(\mathbf{{r'}} = ({r'_i})_{i = 1}^n = (r_{{\sigma ^{ - 1}}(i)}^{ < H(\alpha ) > })_{i = 1}^n\) according to the magnitudes of \(({x_i})_{i = 1}^n\) such that \(\sigma :\{ 1,\cdots ,n\} \rightarrow \{ 1,\cdots ,n\}\) is any suitable permutation satisfying \({x_{\sigma (i)}} \ge {x_{\sigma (j)}}\) whenever \(i < j\).

Step 3.3 As analyzed in Sect. 3.2, with the obtained \({\mathbf{{r}}^{ < {H^ + }(\beta ) > }}\), we should also permute it into a new permuted vector \(\mathbf{{r''}} = ({r''_i})_{i = 1}^n = (r_{{\eta ^{ - 1}}(i)}^{ < {H^ + }(\beta ) > })_{i = 1}^n\) according to the magnitudes of certainties \(({c_i})_{i = 1}^n\) such that \(\eta :\{ 1,\cdots ,n\} \rightarrow \{ 1,\cdots ,n\}\) is any suitable permutation satisfying \({c_{\eta (i)}} \ge {c_{\eta (j)}}\) whenever \(i < j\).


Stage IV BUI aggregation and decision-making (this stage is the virtually identical to Stage IV of the decision procedure in literature [22])

Step 4.1 Take the convex combination form using q to obtain a final weight vector \(\mathbf{{w}} = {q_{OP}}{} \mathbf{{r'}} + {q_{SN}}{} \mathbf{{r''}} + {q_N}{} \mathbf{{a}}\), which can comprehensively embody all the involved preferences and opinions.

Step 4.2 Performing BWAM by (2) with w and \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^n\), obtain one final comprehensively merged BUI granule \((x,c) = BWA{M_\mathbf{{w}}}(\mathbf{{x}},\mathbf{{c}}) = \left( {\sum \nolimits _{i = 1}^n {{w_i}{x_i}} ,\sum \nolimits _{i = 1}^n {{w_i}{c_i}} } \right)\).

Step 4.3 Do some necessary comparison, judgments or decision makings according to the obtained merged BUI granule(s). For example, rules-based decision-making [38,39,40,41] can be suggested to use in a wide range of evaluation problems with uncertainties involved.

6 A Numerical Example in Product Management

In this part, we demonstrate the usage of the previously proposed evaluation procedure with numerical case with the same background of manufacture management as in literature [22] to make some comparison.


Stage I Information, preference collection and preparation

Step 1.1 Still assume that a company needs to decide if one certain product should be considered to manufacture. The decision will be made according to the market share prediction of that product. The predictions are still collected from a group of \(n = 4\) different investigators and they may show differing uncertainties about their respective predictions. This assumption allows the information to be expressed by a vector of BUI granules \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^4 = ((0.6,0.7),(0.5,0.3),(0.3,0.8),(0.8,0.6))\), in which \(({x_i},{c_i})\) is obtained from the information communicated by investigator i so that he feels the market share of the product next year will be around \(100{x_i}\%\) but with confidence about \(100{c_i}\%\).

Step 1.2 Assume the executive consults with a panel of \(M = 6\) experts of this company about the two questions proposed in Sect. 4.3.

Step 1.3 Suppose the six experts give their answers to Question 1 from linguistic variable set \(\{ {l_k}\} _{k = - 2}^2\): \({\alpha _1} = {\alpha _2} = 2\), \({\alpha _3} = {\alpha _5} = 0\), \({\alpha _4} = 1\) and \({\alpha _6} = - 1\), with the orness degrees: \(H({\alpha _1}) = H({\alpha _2}) = 1\), \(H({\alpha _3}) = H({\alpha _5}) = 0.5\), \(H({\alpha _4}) = 0.75\) and \(H({\alpha _6}) = 0.25\).

Step 1.4 Suppose they also give their answers to Question 2 from linguistic variable set \(\{ {l_k}\} _{k = 0}^3\): \({\beta _1} = 2\), \({\beta _2} = {\beta _5} = 0\), \({\beta _3} = 3\), \({\beta _4} = {\beta _6} = 1\), with the orness degrees: \({H^ + }({\beta _1}) = 0.8\), \({H^ + }({\beta _2}) = {H^ + }({\beta _5}) = 0.5\), \({H^ + }({\beta _3}) = 1\), \({H^ + }({\beta _4}) = {H^ + }({\beta _6}) = 0.6\).


Stage II Preference elicitation, orness derivation, and the determination of relative importance between inducing factors and indifference factor

Step 2.1 Take the average of \(H({\alpha _j})\) to obtain an overall orness \(H(\alpha ) = \frac{1}{M}\sum \nolimits _{j = 1}^M {H({\alpha _j})} = 2/3\).

Step 2.2 Take the average of \({H^ + }({\beta _j})\) to obtain \({H^ + }(\beta ) = \frac{1}{M}\sum \nolimits _{j = 1}^M {{H^ + }({\beta _j})} = 2/3\).

Step 2.3 For each expert j (\(j = 1,\cdots ,M\)), from (14), (15) and (16), respectively, to derive a normalized weight vector \({\mathbf{{q}}_j} = ({q_{j\_OP}},{q_{j\_SN}},{q_{j\_N}})\). By computing, we have \({\mathbf{{q}}_1} = (0.5,0.3,0.2)\), \({\mathbf{{q}}_2} = (0.5,0,0.5)\), \({\mathbf{{q}}_3} = (0,0.5,0.5)\), \({\mathbf{{q}}_4} = (0.25,0.1,0.65)\), \({\mathbf{{q}}_5} = (0,0,1)\), \({\mathbf{{q}}_6} = (0.25,0.1,0.65)\). Take the average of \({\mathbf{{q}}_j}\) to obtain \(\mathbf{{q}} = \frac{1}{M}\sum \nolimits _{j = 1}^M {{\mathbf{{q}}_j}} \buildrel \textstyle .\over = (0.25,0.167,0.583)\).


Stage III Weight vector obtaining and permuting

Step 3.1 We still choose to use the recursive family of weight vectors \({\{ {\mathbf{{r}}^{ < \alpha > }}\} _{\alpha \in [0,1]}}\) [34]. Then, we have \({\mathbf{{r}}^{< H(\alpha )> }} = {\mathbf{{r}}^{ < 2/3 > }} = (0.4,0.3,0.2,0.1)\). Likewise, we adopt half of this family of vectors \({\{ {\mathbf{{r}}^{ < \beta > }}\} _{\beta \in [0.5,1]}}\) and then obtain \({\mathbf{{r}}^{< {H^ + }(\beta )> }} = {\mathbf{{r}}^{ < 2/3 > }} = (0.4,0.3,0.2,0.1)\).

Step 3.2 & Step 3.3 After re-permuting we have \(\mathbf{{r'}} = ({r'_i})_{i = 1}^4 = (0.3,0.2,0.1,0.4)\) and \(\mathbf{{r''}} = ({r''_i})_{i = 1}^4 = (0.3,0.1,0.4,0.2)\).


Stage IV BUI aggregation and decision-making

Step 4.1 With \(\mathbf{{a}} = (0.25,0.25,0.25,0.25)\) and obtained \(\mathbf{{q}} \buildrel \textstyle .\over = (0.25,0.167,0.583)\), we get \(\mathbf{{w}} = {q_{OP}}{} \mathbf{{r'}} + {q_{SN}}{} \mathbf{{r''}} + {q_N}{} \mathbf{{a}} = (0.27085,\mathrm{{0}}\mathrm{{.21245}},\mathrm{{0}}\mathrm{{.23755}},\mathrm{{0}}\mathrm{{.27915}})\).

Step 4.2 Lastly, carry out BWAM by (2) with w and \((\mathbf{{x}},\mathbf{{c}}) = ({x_i},{c_i})_{i = 1}^n\), we obtain a final comprehensively merged BUI granule \((x,c) = {\mathsf{{BWAM}}_\mathbf{{w}}}(\mathbf{{x}},\mathbf{{c}}) = \left( {\sum \nolimits _{i = 1}^n {{w_i}{x_i}} ,\sum \nolimits _{i = 1}^n {{w_i}{c_i}} } \right) = (\mathrm{{0}}\mathrm{{.56332}},\mathrm{{0}}\mathrm{{.61086}})\).

Step 4.3 With the obtained resultant BUI granule \((x,c) = (0.4851,0.652)\) we can also do further assessment and take corresponding decisions according to rules-based decision-making [38,39,40,41]. If the threshold is preset such that if the predicted market share is more than 40% with confidence larger than 60%, then the product should be suggested to manufacture. Hence, the BUI granule \((x,c) = (\mathrm{{0}}\mathrm{{.56332}},\mathrm{{0}}\mathrm{{.61086}})\) represents the predicted market share is about 56.332% with approximately 61.086% confidence, and thus the product is suggested to manufacture.

7 Conclusion

If bi-polar preferences and uncertainty arise simultaneously in evaluation, the consideration of relative importance between different inducing factors (inducing variables) is inevitable. Put simply, there usually involves two inducing factors, main values and their certainty degrees, together with indifference which corresponds to Laplace decision criterion. Recently few literatures proposed some decision methods and evaluation procedures that presuppose the invited experts can provide some direct information that can be elicited and transformed into the required relative importance between the two mentioned inducing factors and indifference factor. Nevertheless, apart from some possible cognitive inconsistency, frequently the experts inquired may be not able to provide the information to obtain the required relative importance notwithstanding that the bi-polar preferences can be available.

Based on the adapted two questions for experts to answer, this work proposed three methods, statistic method, distance method, and linguistic variable method, to derive relative importance between the two inducing factors and indifference factor. The first method does this from simple descriptive statistics and thus it might become unsuitable when the number of the invited experts is few. The second method uses the distance from the preference extent to the neutral attitude indirectly to derive the required relative importance; it can be performed with only one expert, but sometimes the preference extent is hard to be answered from the expert due to choosing difficulty or dilemma. The third method using linguistic variable is a compromise between the other two methods.

The detailed evaluation procedure is presented with numerical example to compare the proposed methods with the existing ones in literatures. The methods can be applied in more detailed problems which allow for uncertainty and bi-polar preferences. However, the proposed methods may fail when the vector of inputs cannot be of BUI form; besides, the proposed evaluation processes have not contained any negotiation mechanism when facing the complex group decision-making environment.

Based on the above analysis, this paper proposes some methods to solve the problem that decision makers cannot provide the relative importance needed in the basic uncertain information environment. The specific contributions are as follows:

  1. (1)

    This paper addresses the research gap based on bi-polar preference aggregation of uncertain information, and proposes a sufficient and systematic research method to measure bi-polar preferences involved aggregation operators and processes.

  2. (2)

    This study proposes the method of deriving the special weights to carry out the combination in BUI environment to eliminate or ameliorate cognitive inconsistency.

  3. (3)

    This paper considers three different approaches to elicit some initial information provided by experts, from which we further derive out the two parts of key information, bi-polar preference extents and relative information for inducing factors to obtain relative importance between each inducing factor and hence to perform the required convex combination form.

  4. (4)

    This study provides detailed evaluation procedure and numerical example to illustrate and verify the feasibility.