Skip to main content
SpringerLink
Log in

Bending and free vibration analysis of porous functionally graded sandwich plate with various porosity distributions using an extended layerwise theory

  • Original Article
  • Published:
Archives of Civil and Mechanical Engineering Aims and scope Submit manuscript

Abstract

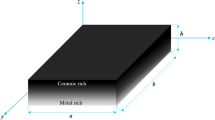
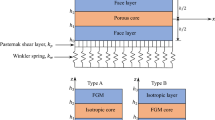
In this paper, for the first time, the bending and free vibration analysis of porous functionally graded sandwich plates with various porosity distributions is investigated using an efficient layerwise model. The present model, proposed recently by the authors, supposes a first-order displacement field for the two face sheets and a higher-order displacement field for the core, thereby ensuring the displacement continuity at the layer's interface. Unlike the conventional layerwise models, the number of degrees of freedom is fixed and does not increase when increasing the number of layers. This is a very important feature compared to the conventional layerwise models and facilitates significantly the engineering analysis. Three different types of porosity distribution including even, logarithmic-uneven, and linear-uneven porosities are considered. The material properties of the FGM sandwich porous plate are graded continuously through the thickness direction according to a power-law function. The numerical analysis is carried out by using an efficient C0 continuous eight-node quadrilateral isoparametric element developed for this purpose. The governing equations are derived according to Hamilton’s principle and solved by employing the finite element method. The robustness and accuracy of the proposed formulation are ascertained by comparing its results with those available by other researchers in the existing literature. Further, a comprehensive parametric study is examined in detail to show the effects of material distribution, aspect ratios, porosity coefficient, side-to-thickness ratio, porosity distribution, core-to-face thickness ratio, boundary conditions, volume fraction index, modes shapes on the bending and free vibration behaviors of symmetric and non-symmetric FGM porous sandwich plate. The numerical results show that these parameters play significant roles in the bending and free vibration behaviors of the FGM sandwich porous plates. Many new results are also reported, which will serve as a benchmark for future analysis of FGM sandwich plates with porosity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Saleh B, Jiang J, Fathi R, Al-hababi T, Xu Q, Wang L, Song D, Ma A. 30 Years of functionally graded materials: an overview of manufacturing methods. Appl Future Chall Compos Part B Eng. 2020;201:108376. https://doi.org/10.1016/j.compositesb.2020.108376.

    Article  Google Scholar 

  2. Haan C, Barfield B, Hayes JJDH, Catchments SS. Sediment control structures. 1994. p. 359–375.

  3. Bansiddhi A, Dunand DC. 7—Titanium and NiTi foams for bone replacement. In: Mallick K, editor. Bone Substitute Biomaterials. Woodhead Publishing: Sawston; 2014. p. 142–79. https://doi.org/10.1533/9780857099037.2.142.

    Chapter  Google Scholar 

  4. Cao S, Yu J. Chapter 15—photocatalysts based on polymeric carbon nitride for solar-to-fuel conversion. In: Yu J, Jaroniec M, Jiang C, editors. Interface science and technology, vol. 31. New York: Elsevier; 2020. p. 475–507. https://doi.org/10.1016/B978-0-08-102890-2.00015-4.

    Chapter  Google Scholar 

  5. Liu PS, Chen GF. Chapter three—application of porous metals. In: Liu PS, Chen GF, editors. Porous materials. Boston: Butterworth-Heinemann; 2014. p. 113–88. https://doi.org/10.1016/B978-0-12-407788-1.00003-4.

    Chapter  Google Scholar 

  6. Rashidi S, Esfahani JA, Hormozi F. Classifications of porous materials for energy applications. Encyclopedia of Smart Materials. 2022;2:774–85. https://doi.org/10.1016/B978-0-12-803581-8.11739-4.

    Article  Google Scholar 

  7. Michailidis N, Tsouknidas A, Lefebvre L-P, Hipke T, Kanetake N. Production, characterization, and applications of porous materials. Adv Mater Sci Eng. 2014;2014:263129.

    Article  Google Scholar 

  8. Ishizaki K, Komarneni S, Nanko M. Applications of porous materials. In: Ishizaki K, Komarneni S, Nanko M, editors. Porous materials: process technology and applications. Boston: Springer; 1998. p. 181–201.

    Chapter  Google Scholar 

  9. Daikh AA, Houari MSA, Belarbi MO, Mohamed SA, Eltaher MA. Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory. Defence Technology. 2021;18(10):1778–809. https://doi.org/10.1016/j.dt.2021.09.011.

    Article  Google Scholar 

  10. Garg A, Chalak HD, Zenkour AM, Belarbi MO, Sahoo R. Bending and free vibration analysis of symmetric and unsymmetric functionally graded CNT reinforced sandwich beams containing softcore. Thin Walled Struct. 2022;170:108626.

    Article  Google Scholar 

  11. Belarbi M-O, Khechai A, Bessaim A, Houari M-S-A, Garg A, Hirane H, Chalak H. Finite element bending analysis of symmetric and non-symmetric functionally graded sandwich beams using a novel parabolic shear deformation theory. Proc Inst Mech Eng Part L J Mater Des Appl. 2021. https://doi.org/10.1177/14644207211005096.

    Article  Google Scholar 

  12. Sayyad AS, Ghugal YM. Modeling and analysis of functionally graded sandwich beams: a review. Mech Adv Mater Struct. 2019;26(21):1776–95.

    Article  Google Scholar 

  13. Garg A, Belarbi M-O, Chalak HD, Chakrabarti A. A review of the analysis of sandwich FGM structures. Compos Struct. 2021;258:113427.

    Article  Google Scholar 

  14. Wang YQ, Wan YH, Zhang YF. Vibrations of longitudinally traveling functionally graded material plates with porosities. Eur J Mech A Solids. 2017;66:55–68.

    Article  MathSciNet  CAS  Google Scholar 

  15. Wattanasakulpong N, Ungbhakorn V. Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp Sci Technol. 2014;32(1):111–20.

    Article  Google Scholar 

  16. Arshid E, Khorshidvand AR. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin Walled Struct. 2018;125:220–33.

    Article  Google Scholar 

  17. Carrera E. Theories and finite elements for multilayered, anisotropic, composite plates and shells. Arch Comput Methods Eng. 2002;9(2):87–140.

    Article  MathSciNet  Google Scholar 

  18. Sayyad AS, Ghugal YM. On the free vibration analysis of laminated composite and sandwich plates: a review of recent literature with some numerical results. Compos Struct. 2015;129:177–201.

    Article  Google Scholar 

  19. Zhou K, Huang X, Tian J, Hua H. Vibration and flutter analysis of supersonic porous functionally graded material plates with temperature gradient and resting on elastic foundation. Compos Struct. 2018;204:63–79.

    Article  Google Scholar 

  20. Li H, Pang F, Chen H, Du Y. Vibration analysis of functionally graded porous cylindrical shell with arbitrary boundary restraints by using a semi analytical method. Compos Part B Eng. 2019;164:249–64.

    Article  Google Scholar 

  21. Chen D, Yang J, Kitipornchai S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos Struct. 2015;133:54–61.

    Article  Google Scholar 

  22. Zhang Y, Jin G, Chen M, Ye T, Yang C, Yin Y. Free vibration and damping analysis of porous functionally graded sandwich plates with a viscoelastic core. Compos Struct. 2020;244:112298.

    Article  Google Scholar 

  23. Xue Y, et al. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int J Mech Sci. 2019;152:346–62.

    Article  Google Scholar 

  24. Rezaei AS, Saidi AR, Abrishamdari M, Mohammadi MHP. Natural frequencies of functionally graded plates with porosities via a simple four variable plate theory: an analytical approach. Thin Walled Struct. 2017;120:366–77.

    Article  Google Scholar 

  25. Medani M, et al. Static and dynamic behavior of (FG-CNT) reinforced porous sandwich plate using energy principle. Steel Compos Struct. 2019;32(5):595–610.

    Google Scholar 

  26. Tran TT, Pham Q-H, Nguyen-Thoi T. Static and free vibration analyses of functionally graded porous variable-thickness plates using an edge-based smoothed finite element method. Def Technol. 2021;17(3):971–86.

    Article  Google Scholar 

  27. Reddy JN. On refined theories of composite laminates. Meccanica. 1990;25(4):230–8.

    Article  MathSciNet  Google Scholar 

  28. Hirane H, Belarbi M-O, Houari MSA, Tounsi A. On the layerwise finite element formulation for static and free vibration analysis of functionally graded sandwich plates. Eng Comput. 2021. https://doi.org/10.1007/s00366-020-01250-1.

    Article  Google Scholar 

  29. Belarbi M-O, Houari MSA, Hirane H, Daikh AA, Bordas SPA. On the finite element analysis of functionally graded sandwich curved beams via a new refined higher order shear deformation theory. Compos Struct. 2022;279:114715.

    Article  Google Scholar 

  30. Pai PF. A new look at shear correction factors and warping functions of anisotropic laminates. Int J Solids Struct. 1995;32(16):2295–313.

    Article  Google Scholar 

  31. Lim T-K, Kim J-H. Thermo-elastic effects on shear correction factors for functionally graded beam. Compos Part B Eng. 2017;123:262–70.

    Article  Google Scholar 

  32. Daikh AA. Temperature dependent vibration analysis of functionally graded sandwich plates resting on Winkler/Pasternak/Kerr foundation. Mater Res Express. 2019;6(6):065702.

    Article  ADS  CAS  Google Scholar 

  33. Daikh AA, Drai A, Bensaid I, Houari MSA, Tounsi A. On vibration of functionally graded sandwich nanoplates in the thermal environment. J Sandw Struct Mater. 2021;23(6):2217–44. https://doi.org/10.1177/1099636220909790.

    Article  Google Scholar 

  34. Belarbi M-O, Houari M-S-A, Daikh AA, Garg A, Merzouki T, Chalak HD, Hirane H. Nonlocal finite element model for the bending and buckling analysis of functionally graded nanobeams using a novel shear deformation theory. Compos Struct. 2021;264:113712. https://doi.org/10.1016/j.compstruct.2021.113712.

    Article  Google Scholar 

  35. Belarbi M-O, Garg A, Houari M-S-A, Hirane H, Tounsi A, Chalak HD. A three-unknown refined shear beam element model for buckling analysis of functionally graded curved sandwich beams. Eng Comput. 2021;. https://doi.org/10.1007/s00366-021-01452-1.

    Article  Google Scholar 

  36. Daikh AA, Zenkour AM. Bending of functionally graded sandwich nanoplates resting on pasternak foundation under different boundary conditions. J Appl Comput Mech. 2020;6(Special Issue):1245–59.

    Google Scholar 

  37. Daikh AA, Houari MSA, Belarbi MO, Chakraverty S, Eltaher MA. Analysis of axially temperature-dependent functionally graded carbon nanotube reinforced composite plates. Eng Comput. 2022;38(3):2533–54. https://doi.org/10.1007/s00366-021-01413-8.

    Article  Google Scholar 

  38. Sayyad AS, Ghugal YM. A unified five-degree-of-freedom theory for the bending analysis of softcore and hardcore functionally graded sandwich beams and plates. J Sandw Struct Mater. 2021;23(2):473–506. https://doi.org/10.1177/1099636219840980.

    Article  Google Scholar 

  39. Yahia SA, Atmane HA, Houari MSA, A. J. S. E. Tounsi, and Mechanics. Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories. Struct Eng Mech Int J. 2015;53(6):1143–65.

    Article  Google Scholar 

  40. Barati MR, Shahverdi H. Aero-hygro-thermal stability analysis of higher-order refined supersonic FGM panels with even and uneven porosity distributions. J Fluids Struct. 2017;73:125–36.

    Article  Google Scholar 

  41. Demirhan PA, Taskin V. Bending and free vibration analysis of Levy-type porous functionally graded plate using state space approach. Compos Part B Eng. 2019;160:661–76.

    Article  Google Scholar 

  42. Daikh AA, Zenkour AM. Effect of porosity on the bending analysis of various functionally graded sandwich plates. Mater Res Express. 2019;6(6): 065703.

    Article  ADS  CAS  Google Scholar 

  43. Daikh AA, Zenkour AM. Free vibration and buckling of porous power-law and sigmoid functionally graded sandwich plates using a simple higher-order shear deformation theory. Mater Res Express. 2019;6(11):115707.

    Article  ADS  CAS  Google Scholar 

  44. Zenkour AM. A quasi-3D refined theory for functionally graded single-layered and sandwich plates with porosities. Compos Struct. 2018;201:38–48.

    Article  Google Scholar 

  45. Zenkour AM, Aljadani MH. Porosity effect on thermal buckling behavior of actuated functionally graded piezoelectric nanoplates. Eur J Mech A Solids. 2019;78:103835.

    Article  MathSciNet  Google Scholar 

  46. Gupta A, Talha M. Influence of porosity on the flexural and free vibration responses of functionally graded plates in thermal environment. Int J Struct Stabil Dyn. 2018;18(01):1850013.

    Article  MathSciNet  Google Scholar 

  47. Shahsavari D, Shahsavari M, Li L, Karami B. A novel quasi-3D hyperbolic theory for free vibration of FG plates with porosities resting on Winkler/Pasternak/Kerr foundation. Aerosp Sci Technol. 2018;72:134–49.

    Article  Google Scholar 

  48. Merdaci S, Belghoul H. High-order shear theory for static analysis of functionally graded plates with porosities. Comptes Rendus Mécanique. 2019;347(3):207–17.

    Article  ADS  Google Scholar 

  49. Xie K, Wang Y, Niu H, Chen H. Large-amplitude nonlinear free vibrations of functionally graded plates with porous imperfection: a novel approach based on energy balance method. Compos Struct. 2020;246:112367.

    Article  Google Scholar 

  50. Mashat DS, Zenkour AM, Radwan AF. A quasi-3D higher-order plate theory for bending of FG plates resting on elastic foundations under hygro-thermo-mechanical loads with porosity. Eur J Mech A Solids. 2020;82:103985.

    Article  MathSciNet  Google Scholar 

  51. Singh SJ, Harsha SP. Thermo-mechanical analysis of porous sandwich S-FGM plate for different boundary conditions using Galerkin Vlasov’s method: a semi-analytical approach. Thin Walled Struct. 2020;150:106668.

    Article  Google Scholar 

  52. Liang C, Wang YQ. A quasi-3D trigonometric shear deformation theory for wave propagation analysis of FGM sandwich plates with porosities resting on viscoelastic foundation. Compos Struct. 2020;247:112478.

    Article  Google Scholar 

  53. Zhao J, Choe K, Xie F, Wang A, Shuai C, Wang Q. Three-dimensional exact solution for vibration analysis of thick functionally graded porous (FGP) rectangular plates with arbitrary boundary conditions. Compos Part B Eng. 2018;155:369–81.

    Article  Google Scholar 

  54. Adhikari B, Dash P, Singh BN. Buckling analysis of porous FGM sandwich plates under various types nonuniform edge compression based on higher order shear deformation theory. Compos Struct. 2020;251:112597.

    Article  Google Scholar 

  55. Guellil M, et al. Influences of porosity distributions and boundary conditions on mechanical bending response of functionally graded plates resting on Pasternak foundation. Steel Compos Struct. 2021;38(1):1–15.

    Google Scholar 

  56. Tahir SI, Chikh A, Tounsi A, Al-Osta MA, Al-Dulaijan SU, Al-Zahrani MM. Wave propagation analysis of a ceramic-metal functionally graded sandwich plate with different porosity distributions in a hygro-thermal environment. Compos Struct. 2021;269:114030.

    Article  Google Scholar 

  57. Van Vinh P, Huy LQ. Finite element analysis of functionally graded sandwich plates with porosity via a new hyperbolic shear deformation theory. Def Technol. 2021. https://doi.org/10.1016/j.dt.2021.03.006.

    Article  Google Scholar 

  58. Sahoo R, Singh BN. Assessment of inverse hyperbolic zigzag theory for buckling analysis of laminated composite and sandwich plates using finite element method. Arch Appl Mech. 2021;91(1):169–86.

    Article  Google Scholar 

  59. Liu N, Jeffers AE. Isogeometric analysis of laminated composite and functionally graded sandwich plates based on a layerwise displacement theory. Compos Struct. 2017;176:143–53.

    Article  Google Scholar 

  60. Pandey S, Pradyumna S. Analysis of functionally graded sandwich plates using a higher-order layerwise theory. Compos Part B Eng. 2018;153:325–36.

    Article  Google Scholar 

  61. Liu M, Cheng Y, Liu J. High-order free vibration analysis of sandwich plates with both functionally graded face sheets and functionally graded flexible core. Compos Part B Eng. 2015;72:97–107.

    Article  Google Scholar 

  62. Dorduncu M. Stress analysis of sandwich plates with functionally graded cores using peridynamic differential operator and refined zigzag theory. Thin Walled Struct. 2020;146:106468.

    Article  Google Scholar 

  63. Di Sciuva M, Sorrenti M. Bending and free vibration analysis of functionally graded sandwich plates: an assessment of the Refined Zigzag Theory. J Sandw Struct Mater. 2021;23(3):760–802. https://doi.org/10.1177/1099636219843970.

    Article  Google Scholar 

  64. Garg A, Chalak HD, Belarbi M-O, Zenkour AM. Hygro-thermo-mechanical based bending analysis of symmetric and unsymmetric power-law, exponential and sigmoidal FG sandwich beams. Mech Adv. Mater Struct. 2021;1–23. https://doi.org/10.1080/15376494.2021.1931993.

  65. Burlayenko VN. A continuum shell element in layerwise models for free vibration analysis of FGM sandwich panels. Contin Mech Thermodyn. 2021;33(4):1385–407.

    Article  ADS  MathSciNet  Google Scholar 

  66. Liew KM, Pan ZZ, Zhang LW. An overview of layerwise theories for composite laminates and structures: development, numerical implementation and application. Compos Struct. 2019;216:240–59.

    Article  Google Scholar 

  67. Liu B, Ferreira A, Xing Y, Neves A. Analysis of functionally graded sandwich and laminated shells using a layerwise theory and a differential quadrature finite element method. Compos Struct. 2016;136:546–53.

    Article  Google Scholar 

  68. Garg A, Chalak HD, Belarbi M-O, Chakrabarti A, Houari M-S-A. Finite element-based free vibration analysis of power-law, exponential and sigmoidal functionally graded sandwich beams. J Inst Eng (India) Ser C. 2021;102:167–1201. https://doi.org/10.1007/s40032-021-00740-5.

    Article  Google Scholar 

  69. Pandey S, Pradyumna S. Thermal shock response of porous functionally graded sandwich curved beam using a new layerwise theory. Mech Based Des Struct Mach. 2021;1–26. https://doi.org/10.1080/15397734.2021.1888297.

  70. Zenkour AM. A comprehensive analysis of functionally graded sandwich plates: part 1—deflection and stresses. Int J Solids Struct. 2005;42(18):5224–42.

    Article  Google Scholar 

  71. Neves AMA, Ferreira AJM, Carrera E, Cinefra M, Jorge RMN, Soares CMM. Static analysis of functionally graded sandwich plates according to a hyperbolic theory considering Zig-Zag and warping effects. Adv Eng Softw. 2012;52:30–43.

    Article  Google Scholar 

Download references

Acknowledgements

This research was supported by The Algerian General Directorate of Scientific Research and Technological Development (DGRSDT) and University of Mohamed Khider of Biskra in Algeria.

Author information

Authors and Affiliations

  1. Laboratoire de Recherche en Génie Civil, LRGC, Université de Biskra, B.P. 145, R.P. 07000, Biskra, Algeria

    Mohamed-Ouejdi Belarbi & Hicham Hirane

  2. Laboratoire d’Etude des Structures et de Mécanique des Matériaux, Département de Génie Civil, Faculté des Sciences et de la Technologie, Université Mustapha Stambouli, B.P. 305, R.P. 29000, Mascara, Algérie

    Ahmed Amine Daikh & Mohammed Sid Ahmed Houari

  3. Department of Civil and Environmental Engineering, The NorthCap University, Gurugram, Haryana, 122017, India

    Aman Garg & H. D. Chalak

  4. Division of Mechanics, Civil Engineering Department, Akdeniz University, Antalya, Turkey

    Ömer Civalek

Authors
  1. Mohamed-Ouejdi Belarbi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmed Amine Daikh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aman Garg
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hicham Hirane
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mohammed Sid Ahmed Houari
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ömer Civalek
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. H. D. Chalak
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohamed-Ouejdi Belarbi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Belarbi, MO., Daikh, A.A., Garg, A. et al. Bending and free vibration analysis of porous functionally graded sandwich plate with various porosity distributions using an extended layerwise theory. Archiv.Civ.Mech.Eng 23, 15 (2023). https://doi.org/10.1007/s43452-022-00551-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s43452-022-00551-0

Keywords

Search

Navigation