Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions

Abstract

Nonlinear partial differential equations (PDEs) are used to model dynamical processes in a large number of scientific fields, ranging from finance to biology. In many applications standard local models are not sufficient to accurately account for certain non-local phenomena such as, e.g., interactions at a distance. Non-local nonlinear PDE models can accurately capture these phenomena, but traditional numerical approximation methods are infeasible when the considered non-local PDE is high-dimensional. In this article we propose two numerical methods based on machine learning and on Picard iterations, respectively, to approximately solve non-local nonlinear PDEs. The proposed machine learning-based method is an extended variant of a deep learning-based splitting-up type approximation method previously introduced in the literature and utilizes neural networks to provide approximate solutions on a subset of the spatial domain of the solution. The Picard iterations-based method is an extended variant of the so-called full history recursive multilevel Picard approximation scheme previously introduced in the literature and provides an approximate solution for a single point of the domain. Both methods are mesh-free and allow non-local nonlinear PDEs with Neumann boundary conditions to be solved in high dimensions. In the two methods, the numerical difficulties arising due to the dimensionality of the PDEs are avoided by (i) using the correspondence between the expected trajectory of reflected stochastic processes and the solution of PDEs (given by the Feynman–Kac formula) and by (ii) using a plain vanilla Monte Carlo integration to handle the non-local term. We evaluate the performance of the two methods on five different PDEs arising in physics and biology. In all cases, the methods yield good results in up to 10 dimensions with short run times. Our work extends recently developed methods to overcome the curse of dimensionality in solving PDEs.

1 Introduction

In this article, we derive numerical schemes to approximately solve high-dimensional non-local nonlinear partial differential equations (PDEs) with Neumann boundary conditions. Such PDEs have been used to describe a variety of processes in physics, engineering, finance, and biology, but can generally not be solved analytically, requiring numerical methods to provide approximate solutions. However, traditional numerical methods are for the most part computationally infeasible for high-dimensional problems, calling for the development of novel approximation methods.

The need for solving non-local nonlinear PDEs has been expressed in various fields as they provide a more general description of the dynamical systems than their local counterparts [1,2,3]. In physics and engineering, non-local nonlinear PDEs are found, e.g., in models of Ohmic heating production [4], in the investigation of the fully turbulent behavior of real flows [5], in phase field models allowing non-local interactions [6,7,8,9], or in phase transition models with conservation of mass [10, 11]; see [1] for further references. In finance, non-local PDEs are used, e.g., in jump-diffusion models for the pricing of derivatives where the dynamics of stock prices are described by stochastic processes experiencing large jumps [3, 12,13,14,15,16,17,18]. Penalty methods for pricing American put options such as in Kou’s jump-diffusion model [19, 20], considering large investors where the agent policy affects the assets prices [15, 21], or considering default risks [22, 23] can further introduce nonlinear terms in non-local PDEs. In economics, non-local nonlinear PDEs appear, e.g., in evolutionary game theory with the so-called replicator-mutator equation capturing continuous strategy spaces [24,25,26,27,28] or in growth models where consumption is non-local [29]. In biology, non-local nonlinear PDEs are used, e.g., to model processes determining the interaction and evolution of organisms. Examples include models of morphogenesis and cancer evolution [30,31,32], models of gene regulatory networks [33], population genetics models with the non-local Fisher–Kolmogorov–Petrovsky–Piskunov (Fisher–KPP) equations [34,35,36,37,38,39,40], and quantitative genetics models where populations are structured on a phenotypic and/or a geographical space [41,42,43,44,45,46,47,48]. In such models, Neumann boundary conditions are used, e.g., to model the effect of the borders of the geographical domain on the movement of the organisms.

Real world systems such as those just mentioned may be of considerable complexity and accurately capturing the dynamics of these systems may require models of high dimensionality [47], leading to complications in obtaining numerical approximations. For example, the number of dimensions of the PDEs may correspond in finance to the number of financial assets (such as stocks, commodities, exchange rates, and interest rates) in the involved portfolio; in evolutionary dynamics, to the dimension of the strategy space; and in biology, to the number of genes modelled [33] or to the dimension of the geographical or the phenotypic space over which the organisms are structured. Standard approximation methods for PDEs such as finite difference approximation methods, finite element methods, spectral Galerkin approximation methods, and sparse grid approximation methods all suffer from the so called curse of dimensionality [49], meaning that their computational costs increase exponentially in the number of dimensions of the PDE under consideration.

Numerical methods exploiting stochastic representations of the solutions of PDEs can in some cases overcome the curse of dimensionality. Specifically, simple Monte Carlo averages of the associated stochastic processes have been proposed a long time ago to solve high-dimensional linear PDEs, such as, e.g., Black–Scholes and Kolmogorov PDEs [50, 51]. Recently, two novel classes of methods have proved successful in dealing with high-dimensional nonlinear PDEs, namely deep learning-based and full history recursive multilevel Picard approximation methods (in the following we will abbreviate full history recursive multilevel Picard by MLP). The explosive success of deep learning in recent years across a wide range of applications [52] has inspired a variety of neural network-based approximation methods for high-dimensional PDEs; see [53,54,55,56,57,58,59] for a survey of this field of research. One class of such methods is based on reformulating the PDE as a stochastic learning problem through suitable Feynman–Kac formulas, cf., e.g., [60,61,62,63,64,65]. In particular, the deep splitting scheme introduced in [65] relies on splitting the differential operator into a linear part (which is reformulated using a suitable Feynman–Kac formula) and a nonlinear part and in that sense belongs to the class of splitting-up methods [66,67,68]. The PDE approximation problem is then decomposed along the time axis into a sequence of separate learning problems. The deep splitting approximation scheme has proved capable of computing reasonable approximations to the solutions of nonlinear PDEs in up to 10000 dimensions. On the other hand, the MLP approximation method, introduced in [69,70,71], utilizes the Feynman–Kac formula to reformulate the PDE problem as a fixed point equation. It further reduces the complexity of the numerical approximation of the time integral through a multilevel Monte Carlo approach. However, neither the deep splitting nor the MLP method can, until now, account for non-localness and Neumann boundary conditions.

The goal of this article is to overcome these limitations and thus we generalize the deep splitting method and the MLP approximation method to approximately solve non-local nonlinear PDEs with Neumann boundary conditions. We handle the non-local term by a plain vanilla Monte Carlo integration and address Neumann boundary conditions by constructing reflected stochastic processes. While the MLP method can, in one run, only provide an approximate solution at a single point $x \in D$ of the spatial domain $D\subseteq \mathbb {R}^d$ where $d\in \mathbb {N}=\{1,2,\dots \}$, the machine learning-based method can in principle provide an approximate solution on a full subset of the spatial domain D (however, cf., e.g., [72,73,74] for results on limitations on the performance of such approximation schemes). We use both methods to solve five non-local nonlinear PDEs arising in models from biology and physics and cross-validate the results of the simulations. We manage to solve the non-local nonlinear PDEs with reasonable accuracy in up to 10 dimensions.

For an account of classical numerical methods for solving non-local PDEs, such as finite differences, finite elements, and spectral methods, we refer the reader to the recent survey [2]. Several machine-learning based schemes for solving non-local PDEs can also be found in the literature. In particular, the physics-informed neural network and deep Galerkin approaches [75, 76], based on representing an approximation of the whole solution of the PDE as a neural network and using automatic differentiation to do a least-squares minimization of the residual of the PDE, have been extended to fractional PDEs and other non-local PDEs [77,78,79,80,81]. While some of these approaches use classical methods susceptible to the curse of dimensionality for the non-local part [77, 78], mesh-free methods suitable for high-dimensional problems have also been investigated [79,80,81].

The literature also contains approaches that are more closely related to the machine learning-based algorithm presented here. Frey and Köck [82, 83] propose an approximation method for non-local semilinear parabolic PDEs with Dirichlet boundary conditions based on and extending the deep splitting method in [65] and carry out numerical simulations for example PDEs in up to 4 dimensions. Castro [84] proposes a numerical scheme for approximately solving non-local nonlinear PDEs based on [64] and proves convergence results for this scheme. Finally, Gonon and Schwab [85] provide theoretical results showing that neural networks with ReLU activation functions have sufficient expressive power to approximate solutions of certain high-dimensional non-local linear PDEs without the curse of dimensionality.

There is a more extensive literature on machine learning-based methods for approximately solving standard PDEs without non-local terms but with various boundary conditions, going back to early works by Lagaris et al. [86, 87] (see also [88]), which employed a grid-based method based on least-squares minimization of the residual and shallow neural networks to solve low-dimensional ODEs and PDEs with Dirichlet, Neumann, and mixed boundary conditions. More recently, approximation methods for PDEs with Neumann (and other) boundary conditions have been proposed using, e.g., physics-informed neural networks [78, 89, 90], the deep Ritz method (based on a variational formulation of certain elliptic PDEs) [91,92,93], or adversarial networks [94].

The remainder of this article is organized as follows. Section 2 discusses a special case of the proposed machine learning-based method, in order to provide a readily comprehensible exposition of the key ideas of the method. Section 3 discusses the general case, which is flexible enough to cover a larger class of PDEs and to allow more sophisticated optimization methods. Section 4 presents our extension of the MLP approximation method to non-local nonlinear PDEs, which we use to obtain reference solutions in Sect. 5. Section 5 provides numerical simulations for five concrete examples of (non-local) nonlinear PDEs.

2 Machine learning-based approximation method in a special case

In this section, we present in Framework 2.11 in Sect. 2.3 below a simplified version of our general machine learning-based algorithm for approximating solutions of non-local nonlinear PDEs with Neumann boundary conditions proposed in Sect. 3 below. This simplified version applies to a smaller class of non-local heat PDEs, specified in Sect. 2.1 below. In Sect. 2.10 we present some elementary results related to the reflection of straight lines on the boundaries of a suitable subset $D\subseteq \mathbb {R}^d$ where $d\in \mathbb {N}$. These serve to elucidate and justify the notations introduced in Framework 2.10 which in turn will be used to describe time-discrete reflected stochastic processes that are employed in our approximations throughout the rest of the article. The simplified algorithm described in Sect. 2.3 below is limited to using neural networks of a particular architecture that are trained using plain vanilla stochastic gradient descent, whereas the full version proposed in Framework 3.1 in Sect. 3.2 below is formulated in such a way that it encompasses a wide array of neural network architectures and more sophisticated training methods, in particular Adam optimization, minibatches, and batch normalization. Stripping away some of these more intricate aspects of the full algorithm is intended to exhibit more acutely the central ideas in the proposed approximation method.

The simplified algorithm described in this section as well as the more general version proposed in Framework 3.1 in Sect. 3.2 below are based on the deep splitting method introduced in Beck et al. [65], which combines operator splitting with a previous deep learning-based approximation method for Kolmogorov PDEs [62]; see also Beck et al. [53, Sections 2 and 3] for an exposition of these methods.

2.1 Partial differential equations (PDEs) under consideration

Let $T \in (0,\infty )$, $d \in \mathbb {N}$, let $D\subseteq \mathbb {R}^d$ be a sufficiently regular closed set, let¹$\textbf{n} :\partial _D\rightarrow \mathbb {R}^d$ be a suitable outer unit normal vector field associated to $D$, let $g\in C(D, \mathbb {R})$, let $\nu _x :\mathcal {B}(D) \rightarrow [0,1]$, $x \in D$, be probability measures, let $f :\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ be measurable, let $u=(u(t,x))_{(t,x)\in [0,T]\times D}\in C^{1,2}([0,T]\times D,\mathbb {R})$ have at most polynomially growing partial derivatives, assume² for every $t\in (0,T]$, $x\in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$, and assume for every $t\in [0,T]$, $x\in D$ that $u(0,x)=g(x)$, $\int _D|{f(u(t,x),u(t,\textbf{x})) } | \, \nu _x(\textrm{d}\textbf{x}) < \infty$, and

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x)&= (\Delta _x u)(t,x)+\int _{D} f(u(t,x),u(t,\textbf{x})) \, \nu _x(\textrm{d}\textbf{x}) . \end{aligned} \end{aligned}$$

(1)

Our goal in this section is to approximately calculate under suitable hypotheses the solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (1).

2.2 Reflection principle for the simulation of time discrete reflected processes

Lemma 2.1

Let $d\in \mathbb {N}$, let $D\subseteq \mathbb {R}^d$, let $x,y,\mathfrak {c}\in \mathbb {R}^d$ satisfy

$$\begin{aligned} \mathfrak {c}= x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(2)

and assume $\mathfrak {c}\notin \{x,y\}$. Then $\mathfrak {c}\in \partial _D$.

Proof of Lemma 2.1

Throughout this proof let $t\in [0,1]$ satisfy

$$\begin{aligned} t = \inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\}) . \end{aligned}$$

(3)

Observe that (2) and (3) imply that

$$\begin{aligned} \mathfrak {c}= x + t(y-x) . \end{aligned}$$

(4)

This and the assumption that $\mathfrak {c}\notin \{x,y\}$ show that

$$\begin{aligned} t\notin \{0,1\}. \end{aligned}$$

(5)

Combining this with (3) ensures that for every $s\in [0,t)$ it holds that

$$\begin{aligned} x+s(y-x)\in D. \end{aligned}$$

(6)

Next observe that (3) and (5) imply that for every $\varepsilon \in (0,\infty )$ there exists $s\in [t,t+\varepsilon )$ such that

$$\begin{aligned} x+s(y-x)\notin D . \end{aligned}$$

(7)

Combining this with (4), (5) and (6) shows that $\mathfrak {c}\in \partial _D$. The proof of Lemma 2.1 is thus complete. $\square$

Lemma 2.2

Let $d\in \mathbb {N}$, $x,n\in \mathbb {R}^d$ and assume $\Vert {n} \Vert =1$. Then

• (i) it holds that $\Vert {n-x} \Vert = \Vert {n+x-2\langle {x,n} \rangle n} \Vert$ and

• (ii) it holds that $\Vert {x-2\langle {x,n} \rangle n} \Vert =\Vert {x} \Vert$.

Proof of Lemma 2.2

Throughout this proof let $y\in \mathbb {R}^d$ satisfy

$$\begin{aligned} y = x- \langle {x,n} \rangle n. \end{aligned}$$

(8)

Observe that the assumption that $\Vert {n} \Vert =1$ implies that

$$\begin{aligned} \langle {y,n} \rangle = \langle {x,n} \rangle -\langle {x,n} \rangle \langle {n,n} \rangle = \langle {x,n} \rangle -\langle {x,n} \rangle \Vert {n} \Vert ^2 = 0 . \end{aligned}$$

(9)

This ensures that for every $a,b\in \mathbb {R}$ it holds that

$$\begin{aligned} \begin{aligned} \Vert {an+by} \Vert ^2&= \langle {an+by,an+by} \rangle \\ {}&= \langle {an,an} \rangle +\langle {an,by} \rangle +\langle {by,an} \rangle +\langle {by,by} \rangle \\ {}&= a^2\langle {n,n} \rangle +2ab\langle {y,n} \rangle +b^2\langle {y,y} \rangle \\ {}&= a^2\Vert {n} \Vert ^2 + b^2\Vert {y} \Vert ^2 . \end{aligned} \end{aligned}$$

(10)

Hence, we obtain that

$$\begin{aligned} \begin{aligned} \Vert {n+x-2\langle {x,n} \rangle n} \Vert ^2&= \Vert {n+ y - \langle {x,n} \rangle n} \Vert ^2 \\ {}&= \Vert {(1-\langle {x,n} \rangle )n+ y} \Vert ^2 \\ {}&= (1-\langle {x,n} \rangle )^2\Vert {n} \Vert ^2 + \Vert {y} \Vert ^2 \\ {}&= \Vert {(1-\langle {x,n} \rangle )n- y} \Vert ^2 \\ {}&= \Vert {n- y - \langle {x,n} \rangle n} \Vert ^2 \\ {}&= \Vert {n- x} \Vert ^2 . \end{aligned} \end{aligned}$$

(11)

This proves item (i). Next note that (10) implies that

$$\begin{aligned} \Vert {x-2\langle {x,n} \rangle n} \Vert ^2 = \Vert {y - \langle {x,n} \rangle n} \Vert ^2 = \langle {x,n} \rangle ^2\Vert {n} \Vert ^2 + \Vert {y} \Vert ^2 = \Vert {y + \langle {x,n} \rangle n} \Vert ^2 = \Vert {x} \Vert ^2 . \end{aligned}$$

(12)

This demonstrates item (ii). The proof of Lemma 2.2 is thus complete. $\square$

Lemma 2.3

Let $d\in \mathbb {N}$, let $D\subseteq \mathbb {R}^d$ be a closed set, let $\mathfrak {c}:(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(13)

let $\textbf{n}:\partial _D\rightarrow \{x\in \mathbb {R}^d:\Vert {x} \Vert =1\}$ and $\mathscr {R}:(\mathbb {R}^d)^2\rightarrow (\mathbb {R}^d)^2$ satisfy for every $x,y\in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\textbf{n}(\mathfrak {c}(x,y))}\big \rangle \textbf{n}(\mathfrak {c}(x,y)) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x, y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(14)

and let $x_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0=\mathbb {N}\cup \{0\}$, and $y_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, satisfy for every $n\in \mathbb {N}$ that

$$\begin{aligned} (x_n,y_n) = \mathscr {R}(x_{n-1},y_{n-1}) \end{aligned}$$

(15)

(cf. Lemma 2.1). Then

• (i) it holds for every $n\in \mathbb {N}$ that $x_n = \mathfrak {c}(x_{n-1},y_{n-1})$,

• (ii) it holds for every $n,k\in \mathbb {N}_0$ with $x_n\in D$ that $x_{n+k}\in D$,

• (iii) it holds for every $n,k\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}$ that $(x_{n+k},y_{n+k}) = (x_n,y_n)$,

• (iv) it holds for every $n\in \mathbb {N}$ that $\Vert {x_n-y_{n-1}} \Vert = \Vert {x_n-y_n} \Vert$,

• (v) it holds that

  $$\begin{aligned} \sum _{i=0}^\infty \Vert {x_i - x_{i+1}} \Vert \le \Vert {x_0 - y_0} \Vert . \end{aligned}$$

  (16)

Proof of Lemma 2.3

First, observe that (14) and (15) imply item (i). Moreover, note that (13) ensures that for every $v,w\in \mathbb {R}^d$ with $v\ne w$ and $\mathfrak {c}(v,w)=w$ it holds that

$$\begin{aligned} \inf (\{r\in [0,1]:v+r(w-v)\notin D\}\cup \{1\}) = 1 . \end{aligned}$$

(17)

The assumption that D is a closed set hence shows that for every $v,w\in \mathbb {R}^d$ with $v\ne w$ and $\mathfrak {c}(v,w)=w$ it holds that $w \in D$. Combining this and the fact that for every $v\in \mathbb {R}^d$ it holds that $\mathfrak {c}(v,v)=v$ with Lemma 2.1 and the assumption that D is a closed set proves that for every $v\in D$, $w\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \mathfrak {c}(v,w)\in D. \end{aligned}$$

(18)

Item (i) and induction hence establish item (ii). Next observe that (14) and (15) imply that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1}) = x_{n-1}$ it holds that

$$\begin{aligned} (x_n,y_n) = \mathscr {R}(x_{n-1},y_{n-1}) = (x_{n-1},y_{n-1}) . \end{aligned}$$

(19)

Induction therefore ensures that for every $n\in \mathbb {N}$, $k\in \mathbb {N}_0$ with $\mathfrak {c}(x_{n-1},y_{n-1}) = x_{n-1}$ it holds that

$$\begin{aligned} (x_{n+k},y_{n+k}) = (x_n,y_n) = (x_{n-1},y_{n-1}) . \end{aligned}$$

(20)

In addition, note that (14) and (15) show that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1}) = y_{n-1}$ it holds that

$$\begin{aligned} (x_n,y_n) = \mathscr {R}(x_{n-1},y_{n-1}) = (y_{n-1},y_{n-1}) . \end{aligned}$$

(21)

Hence, we obtain that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1}) = y_{n-1}$ it holds that

$$\begin{aligned} \mathfrak {c}(x_n,y_n) = \mathfrak {c}(y_{n-1},y_{n-1}) = y_{n-1} = x_n . \end{aligned}$$

(22)

This and (20) demonstrate that for every $n,k\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1}) = y_{n-1}$ it holds that

$$\begin{aligned} (x_{n+k},y_{n+k}) = (x_n,y_n) . \end{aligned}$$

(23)

Combining this with (20) establishes item (iii). In the next step we observe that (14) and (15) ensure that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}$ it holds that $y_n = y_{n-1}$. Therefore, we obtain that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \Vert {x_n - y_n} \Vert = \Vert {x_n - y_{n-1}} \Vert . \end{aligned}$$

(24)

Next note that Lemma 2.1, item (ii) in Lemma 2.2 (applied for every $v\in \mathbb {R}^d$, $w\in \{u\in \mathbb {R}^d:\mathfrak {c}(v,u)\notin \{v,u\}\}$ with $d\curvearrowleft d$, $x\curvearrowleft w-\mathfrak {c}(v,w)$, $n\curvearrowleft \textbf{n}(\mathfrak {c}(v,w))$ in the notation of Lemma 2.2), and (14) show that for every $v,w,u,z\in \mathbb {R}^d$ with $\mathfrak {c}(v,w)\notin \{v,w\}$ and $(u,z) = \mathscr {R}(v,w)$ it holds that

$$\begin{aligned} \Vert {z-\mathfrak {c}(v,w)} \Vert = \Vert {w-\mathfrak {c}(v,w)-2\langle {w-\mathfrak {c}(v,w),\textbf{n}(\mathfrak {c}(v,w))} \rangle \textbf{n}(\mathfrak {c}(v,w))} \Vert = \Vert {w-\mathfrak {c}(v,w)} \Vert . \end{aligned}$$

(25)

This, item (i), and (15) prove that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \Vert {x_n-y_n} \Vert = \Vert {y_n - \mathfrak {c}(x_{n-1},y_{n-1})} \Vert = \Vert {y_{n-1} - \mathfrak {c}(x_{n-1},y_{n-1})} \Vert = \Vert {x_n-y_{n-1}} \Vert . \end{aligned}$$

(26)

Combining this with (24) establishes item (iv). Moreover, observe that item (i) and (13) ensure that for every $n\in \mathbb {N}$ there exists $t\in [0,1]$ such that $x_n=x_{n-1}+t(y_{n-1}-x_{n-1})$. This and item (iv) show that for every $n\in \mathbb {N}$ there exists $t\in [0,1]$ such that

$$\begin{aligned}{} & {} \Vert {x_{n-1}-x_n} \Vert +\Vert {x_n-y_n} \Vert \nonumber \\{} & {} \quad = \Vert {x_{n-1}-x_n} \Vert +\Vert {x_n-y_{n-1}} \Vert \nonumber \\{} & {} \quad =\Vert {x_{n-1}-(x_{n-1}+t(y_{n-1}-x_{n-1}))} \Vert +\Vert {(x_{n-1}+t(y_{n-1}-x_{n-1}))-y_{n-1}} \Vert \nonumber \\{} & {} \quad = \Vert {-t(y_{n-1}-x_{n-1})} \Vert +\Vert {(t-1)(y_{n-1}-x_{n-1})} \Vert \nonumber \\{} & {} \quad = t\Vert {y_{n-1}-x_{n-1}} \Vert +(1-t)\Vert {y_{n-1}-x_{n-1}} \Vert \nonumber \\{} & {} \quad = \Vert {x_{n-1}-y_{n-1}} \Vert . \end{aligned}$$

(27)

Combining this with induction proves that for every $n\in \mathbb {N}$ it holds that

$$\begin{aligned} \Vert {x_0-y_0} \Vert = \left( \sum _{i=1}^n \Vert {x_{i-1} - x_i} \Vert \right) + \Vert {x_n-y_n} \Vert . \end{aligned}$$

(28)

This implies item (v). The proof of Lemma 2.3 is thus complete. $\square$

Proposition 2.4

Let $d\in \mathbb {N}$, let $\mathfrak {c}:(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :\Vert {x + r(y - x)} \Vert >1\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(29)

let $\mathscr {R}:(\mathbb {R}^{ d })^2 \rightarrow ( \mathbb {R}^{ d })^2$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\mathfrak {c}(x,y)}\big \rangle \mathfrak {c}(x,y) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x, y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(30)

and let $x_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, and $y_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, satisfy for every $n\in \mathbb {N}$ that

$$\begin{aligned} (x_{n},y_{n}) = \mathscr {R}(x_{n-1},y_{n-1}) . \end{aligned}$$

(31)

Then there exists $N\in \mathbb {N}_0$ such that for every $n\in \mathbb {N}_0\cap [N,\infty )$ it holds that

$$\begin{aligned} (x_{n},y_{n}) = (x_{N},y_{N}) . \end{aligned}$$

(32)

Proof of Proposition 2.4

Throughout this proof let $t_n\in [0,1]$, $n\in \mathbb {N}_0$, satisfy for every $n\in \mathbb {N}_0$ that

$$\begin{aligned} t_n = \inf ( \{r \in [0,1] :\Vert {x_{n} + r(y_{n} - x_{n})} \Vert >1\}\cup \{1\}) . \end{aligned}$$

(33)

Note that Lemma 2.1 (applied for every $n\in \{m\in \mathbb {N}:\mathfrak {c}(x_{m-1},y_{m-1})\notin \{x_{m-1},y_{m-1}\}\}$ with $d\curvearrowleft d$, $D\curvearrowleft \{x\in \mathbb {R}^d:\Vert {x} \Vert \le 1\}$, $x\curvearrowleft x_{n-1}$, $y\curvearrowleft y_{n-1}$, $\mathfrak {c}\curvearrowleft \mathfrak {c}(x_{n-1},y_{n-1})$ in the notation of Lemma 2.1) implies that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \Vert {\mathfrak {c}(x_{n-1},y_{n-1})} \Vert =1 . \end{aligned}$$

(34)

Next observe that item (i) in Lemma 2.1, (29), and (33) show that for every $n\in \mathbb {N}$ it holds that

$$\begin{aligned} x_n = \mathfrak {c}(x_{n-1},y_{n-1}) = x_{n-1} + t_{n-1}(y_{n-1}-x_{n-1}) . \end{aligned}$$

(35)

This and (30) ensure that for every $n\in \mathbb {N}$, $t\in \mathbb {R}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \begin{aligned}&x_{n} + t(y_{n} - x_{n}) \\&\quad = x_{n} + t\big ({y_{n-1} - 2\big \langle {y_{n-1} - \mathfrak {c}(x_{n-1},y_{n-1}),\mathfrak {c}(x_{n-1},y_{n-1})}\big \rangle \mathfrak {c}(x_{n-1},y_{n-1}) - x_{n}}\big ) \\&\quad = x_{n} + t(y_{n-1} - x_{n}) - 2t\big \langle {y_{n-1} - \mathfrak {c}(x_{n-1},y_{n-1}),\mathfrak {c}(x_{n-1},y_{n-1})}\big \rangle \mathfrak {c}(x_{n-1},y_{n-1}) \\&\quad = x_{n} + t(y_{n-1} - x_{n}) - 2\langle {t(y_{n-1}-x_{n}),x_{n}} \rangle x_{n} . \end{aligned} \end{aligned}$$

(36)

Combining this, (34), and (35) with item (i) in Lemma 2.2 (applied for every $t\in \mathbb {R}$, $n\in \{m\in \mathbb {N}:\mathfrak {c}(x_{m-1},y_{m-1})\notin \{x_{m-1},y_{m-1}\}\}$ with $d\curvearrowleft d$, $x\curvearrowleft t(y_{n-1}-x_{n})$, $n\curvearrowleft x_{n}$ in the notation of Lemma 2.2) establishes that for every $n\in \mathbb {N}$, $t\in \mathbb {R}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \Vert {x_{n} + t(y_{n} - x_{n})} \Vert = \Vert {x_{n} - t(y_{n-1} - x_{n})} \Vert . \end{aligned}$$

(37)

In the next step we note that (33) implies that for every $n\in \mathbb {N}_0$, $t\in [0,t_n]$ with $t_n>0$ it holds that

$$\begin{aligned} \Vert {x_{n} + t(y_{n}-x_{n})} \Vert \le 1 . \end{aligned}$$

(38)

The fact that for every $s\in [0,1)$, $t\in [0,\tfrac{s}{1-s}]$ it holds that $s-t(1-s)\in [0,s]$ and (35) hence ensure that for every $n\in \mathbb {N}$, $t\in [0,1]$ with $t_{n-1}\in (0,1)$ and $t\le \tfrac{t_{n-1}}{1-t_{n-1}}$ it holds that

$$\begin{aligned} \begin{aligned}&\Vert {x_{n} - t(y_{n-1} -x_{n})} \Vert \\&\quad = \Vert {x_{n-1} +t_{n-1}(y_{n-1} - x_{n-1}) - t(y_{n-1} - x_{n-1} -t_{n-1}(y_{n-1} - x_{n-1}))} \Vert \\&\quad = \Vert {x_{n-1} + (t_{n-1} - t(1 -t_{n-1}))(y_{n-1} - x_{n-1})} \Vert \le 1 . \end{aligned} \end{aligned}$$

(39)

Combining this with (37) shows that for every $n\in \mathbb {N}$, $t\in [0,1]$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ and $t\le \tfrac{t_{n-1}}{1-t_{n-1}}$ it holds that

$$\begin{aligned} \Vert {x_{n} + t(y_{n} - x_{n})} \Vert \le 1 . \end{aligned}$$

(40)

Hence, we obtain that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} t_n\ge \min \big \{{1,\tfrac{t_{n-1}}{1-t_{n-1}}}\big \} . \end{aligned}$$

(41)

Furthermore, note that (35) implies that for every $n\in \mathbb {N}_0$ with $\mathfrak {c}(x_{n},y_{n})\notin \{x_{n},y_{n}\}$ it holds that

$$\begin{aligned} x_{n}\ne y_{n} \qquad \text {and}\qquad t_{n}\in (0,1) . \end{aligned}$$

(42)

Item (iv) in Lemma 2.3, (35), and (41) therefore establish that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ and $\mathfrak {c}(x_{n},y_{n})\notin \{x_{n},y_{n}\}$ it holds that

$$\begin{aligned} \begin{aligned} \Vert {x_{n+1} - x_{n}} \Vert&= \Vert {t_n(y_{n} - x_{n})} \Vert \\ {}&\ge \tfrac{t_{n-1}}{1-t_{n-1}}\Vert {y_{n} - x_{n}} \Vert \\ {}&= \tfrac{t_{n-1}}{1-t_{n-1}}\Vert {y_{n-1} - x_{n}} \Vert \\ {}&= \tfrac{t_{n-1}}{1-t_{n-1}}\Vert {y_{n-1} - x_{n-1} - t_{n-1}(y_{n-1} - x_{n-1})} \Vert \\ {}&= \Vert {t_{n-1}(y_{n-1} - x_{n-1})} \Vert \\ {}&= \Vert {x_{n} - x_{n-1}} \Vert . \end{aligned} \end{aligned}$$

(43)

Moreover, observe that (42) ensures that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \Vert {x_{n} - x_{n-1}} \Vert = t_{n-1}\Vert {y_{n-1} - x_{n-1}} \Vert >0 . \end{aligned}$$

(44)

Combining this and (43) with item (v) in Lemma 2.3 demonstrates that there exists $n\in \mathbb {N}_0$ such that $\mathfrak {c}(x_n,y_n)\in \{x_n,y_n\}$. Combining this with item (iii) in Lemma 2.3 establishes that there exists $N\in \mathbb {N}_0$ such that for every $n\in \mathbb {N}_0\cap [N,\infty )$ it holds that

$$\begin{aligned} (x_{n},y_{n}) = (x_{N},y_{N}) . \end{aligned}$$

(45)

The proof of Proposition 2.4 is thus complete. $\square$

Lemma 2.5

Let $d\in \mathbb {N}$, for every $k\in \{1,2,\dots ,d\}$ let $\mathfrak {a}_k^0\in \mathbb {R}$, $\mathfrak {a}_k^1\in (\mathfrak {a}_k^0,\infty )$, let $D=[\mathfrak {a}_1^0,\mathfrak {a}_1^1]\times [\mathfrak {a}_2^0,\mathfrak {a}_2^1]\times \cdots \times [\mathfrak {a}_d^0,\mathfrak {a}_d^1]\subseteq \mathbb {R}^d$, let $e_1=(1,0,0,\dots ,0)$, $e_2=(0,1,0,\dots ,0)$, $\dots$, $e_d=(0,\dots ,0,0,1)\in \mathbb {R}^d$, let $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$ satisfy for every $x=(x_1,\dots ,x_d)\in \partial _D$, $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:x_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

$$\begin{aligned} \begin{aligned} \textbf{n}(x) = {\left\{ \begin{array}{ll} -e_k&{}:x_k=\mathfrak {a}_k^0\\ e_k&{}:x_k=\mathfrak {a}_k^1, \end{array}\right. } \end{aligned} \end{aligned}$$

(46)

let $\mathfrak {c}:(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(47)

let $\mathscr {R}:(\mathbb {R}^d)^2\rightarrow (\mathbb {R}^d)^2$ satisfy for every $x,y\in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\textbf{n}(\mathfrak {c}(x,y))}\big \rangle \textbf{n}(\mathfrak {c}(x,y)) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x, y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(48)

for every $a\in \mathbb {R}$, $b\in (a,\infty )$ let $r_{a,b}:\mathbb {R}\rightarrow \mathbb {Z}$ satisfy for every $x\in (-\infty ,a)$, $y\in (b,\infty )$ that

$$\begin{aligned} |{r_{a,b}(2a-x)} |< |{r_{a,b}(x)} | \qquad \text {and}\qquad |{r_{a,b}(2b-x)} | < |{r_{a,b}(y)} |, \end{aligned}$$

(49)

let $\mathfrak {r}:\mathbb {R}^d\rightarrow \mathbb {N}_0$ satisfy for every $x=(x_1,\dots ,x_d)\in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {r}(x) = \sum _{k=1}^d |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(x_k)} |, \end{aligned}$$

(50)

and let $u\in \mathbb {R}^d$, $x=(x_1,\dots ,x_d),\,y=(y_1,\dots ,y_d),\,c=(c_1,\dots ,c_d),\,v=(v_1,\dots ,v_d)\in \mathbb {R}^d$ satisfy $c=\mathfrak {c}(x,y)\notin \{x,y\}$ (cf. Lemma 2.1). Then

• (i) it holds that $c\in \partial _D=\{z=(z_1,\dots ,z_d)\in D:(\exists \,k\in \{1,2,\dots ,d\}:z_k\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\})\}$,

• (ii) it holds for every $i,k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

  $$\begin{aligned} v_i = {\left\{ \begin{array}{ll} y_i &{} :i\ne k\\ 2c_k-y_k &{}:i=k, \end{array}\right. } \end{aligned}$$

  (51)

• (iii) it holds that

  $$\begin{aligned} \mathfrak {c}(u,v) = u \qquad \text {or}\qquad \mathfrak {r}(v)<\mathfrak {r}(y) , \end{aligned}$$

  (52)

  and

• (iv) it holds for every $k\in \{1,2,\dots ,d\}$ with $\{k\} = \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

  $$\begin{aligned} x_k\ne y_k ,\qquad \mathfrak {c}(u,v) \ne u ,\qquad \text {and}\qquad \mathfrak {r}(v)<\mathfrak {r}(y) . \end{aligned}$$

  (53)

Proof of Lemma 2.5

Throughout this proof let $t\in [0,1]$ satisfy

$$\begin{aligned} t = \inf (\{r\in [0,1]:x+r(y-x)\notin D\}\cup \{1\}) . \end{aligned}$$

(54)

Note that Lemma 2.1 and the assumption that $c\notin \{x,y\}$ imply item (i). Next observe that (46) ensures that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}\}$ it holds that

$$\begin{aligned} y-\langle {y-c,\textbf{n}(c)} \rangle \textbf{n}(c) = y - 2\langle {y-c,e_k} \rangle e_k = y - 2(y_k-c_k)e_k . \end{aligned}$$

(55)

This, (48), and the assumption that $c\notin \{x,y\}$ show that for every $i,k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ it holds that

$$\begin{aligned} v_i = {\left\{ \begin{array}{ll} y_i &{} :i\ne k\\ y_k - 2(y_k-c_k) &{}:i=k \end{array}\right. } = {\left\{ \begin{array}{ll} y_i &{} :i\ne k\\ 2c_k-y_k &{}:i=k. \end{array}\right. } \end{aligned}$$

(56)

Hence, we obtain item (ii). Next note that (47) implies that for every $k\in \{1,2,\dots ,d\}$ with $x_k=y_k$ it holds that $x_k=c_k=y_k$. Item (ii) therefore demonstrates that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $x_k=y_k$ it holds that

$$\begin{aligned} v=y. \end{aligned}$$

(57)

Moreover, observe that the assumption that $c=\mathfrak {c}(x,y)\notin \{x,y\}$, (47), and (54) ensure that

$$\begin{aligned} t\in (0,1) . \end{aligned}$$

(58)

The fact that $D\subseteq \mathbb {R}^d$ is a closed, convex set, (54), and the assumption that $c\ne y$ hence proves that for every $s\in (t,1]$ it holds that

$$\begin{aligned} x+s(y-x)\notin D . \end{aligned}$$

(59)

In addition, note that (48) implies that

$$\begin{aligned} u=c . \end{aligned}$$

(60)

This, (57), (58), and (59) show that for every $k\in \{1,2,\dots ,d\}$, $s\in (0,1]$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $x_k=y_k$ it holds that

$$\begin{aligned} u+s(v-u)= & {} c+s(y-c) \nonumber \\= & {} x+t(y-x) + s(y-x-t(y-x)) \nonumber \\= & {} x+(t+s(1-t))(y-x) \notin D . \end{aligned}$$

(61)

Hence, we obtain that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $x_k=y_k$ it holds that

$$\begin{aligned} \mathfrak {c}(u,v)= u . \end{aligned}$$

(62)

Next observe that (47) and (58) ensure that for every $k\in \{1,2,\dots ,d\}$ with $x_k\ne y_k$ it holds that

$$\begin{aligned} x_k<c_k<y_k \qquad \text {or}\qquad y_k<c_k<x_k . \end{aligned}$$

(63)

Furthermore, note that (58) implies that

$$\begin{aligned} x\in D. \end{aligned}$$

(64)

This and (63) show that for every $k\in \{1,2,\dots ,d\}$ with $x_k\ne y_k$ and $c_k=\mathfrak {a}_k^0$ it holds that

$$\begin{aligned} y_k<c_k=\mathfrak {a}_k^0 . \end{aligned}$$

(65)

Combining this with item (ii), (49), and (50) proves that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$, $x_k\ne y_k$, and $c_k=\mathfrak {a}_k^0$ it holds that

$$\begin{aligned} \begin{aligned} \mathfrak {r}(v) =&\left[ \sum _{i=1}^d |{r_{\mathfrak {a}_i^0,\mathfrak {a}_i^1}(y_i)} |\right] - |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(y_k)} | + |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(2\mathfrak {a}_k^0-y_k)} |\\ <&\sum _{i=1}^d |{r_{\mathfrak {a}_i^0,\mathfrak {a}_i^1}(y_i)} | = \mathfrak {r}(y) . \end{aligned} \end{aligned}$$

(66)

In addition, observe that (64) and (63) imply that for every $k\in \{1,2,\dots ,d\}$ with $x_k\ne y_k$ and $c_k=\mathfrak {a}_k^1$ it holds that

$$\begin{aligned} \mathfrak {a}_k^1=c_k<y_k . \end{aligned}$$

(67)

Combining this with item (ii), (49), and (50) shows that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$, $x_k\ne y_k$, and $c_k=\mathfrak {a}_k^1$ it holds that

$$\begin{aligned} \begin{aligned} \mathfrak {r}(v) =&\left[ \sum _{i=1}^d |{r_{\mathfrak {a}_i^0,\mathfrak {a}_i^1}(y_i)} |\right] - |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(y_k)} | + |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(2\mathfrak {a}_k^1-y_k)} |\\ <&\sum _{i=1}^d |{r_{\mathfrak {a}_i^0,\mathfrak {a}_i^1}(y_i)} | = \mathfrak {r}(y) . \end{aligned} \end{aligned}$$

(68)

This and (66) establish that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $x_k\ne y_k$ it holds that

$$\begin{aligned} \mathfrak {r}(v)<\mathfrak {r}(y) . \end{aligned}$$

(69)

Combining this with (62) proves item (iii). Next note that the fact that for every $z=(z_1,\dots ,z_d)\in D$, $k\in \{1,2,\dots ,d\}$ with $z_k\notin \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}$ it holds that $z_k\in (\mathfrak {a}_k^0,\mathfrak {a}_k^1)$ implies that for every $k\in \{1,2,\dots ,d\}$ with $c_k\notin \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}$ there exists $T\in (0,\infty )$ such that for every $t\in [0,T]$ it holds that

$$\begin{aligned} c_k + t(v_k-c_k) \in [\mathfrak {a}_k^0,\mathfrak {a}_k^1] . \end{aligned}$$

(70)

Moreover, observe that (47) demonstrates that for every $k\in \{1,2,\dots ,d\}$ it holds that

$$\begin{aligned} x_k\le c_k\le y_k \qquad \text {or}\qquad y_k\le c_k\le x_k. \end{aligned}$$

(71)

This and (64) show that for every $k\in \{1,2,\dots ,d\}$ with $c_k\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}$ it holds that

$$\begin{aligned} y_k\le c_k=\mathfrak {a}_k^0 \qquad \text {or}\qquad \mathfrak {a}_k^1 = c_k \le y_k . \end{aligned}$$

(72)

This and item (ii) ensure that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $c_k=\mathfrak {a}_k^0$ it holds that

$$\begin{aligned} \begin{aligned} v_k = 2\mathfrak {a}_k^0 - y_k \ge \mathfrak {a}_k^0 . \end{aligned} \end{aligned}$$

(73)

In addition, observe that item (ii) and (72) demonstrate that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ and $c_k=\mathfrak {a}_k^1$ it holds that

$$\begin{aligned} \begin{aligned} v_k = 2\mathfrak {a}_k^1 - y_k \le \mathfrak {a}_k^1 . \end{aligned} \end{aligned}$$

(74)

Combining this and (73) proves that for every $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ there exists $T\in (0,\infty )$ such that for every $t\in [0,T]$ it holds that

$$\begin{aligned} c_k + t(v_k - c_k) \in [\mathfrak {a}_k^0,\mathfrak {a}_k^1]. \end{aligned}$$

(75)

This and (70) establish that for every $k\in \{1,2,\dots ,d\}$ with $\{k\}=\{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ there exists $T\in (0,\infty )$ such that for every $t\in [0,T]$ it holds that

$$\begin{aligned} c + t(v - c) \in D. \end{aligned}$$

(76)

Moreover, note that item (ii) and the assumption that $c\ne y$ show that $v\ne \mathfrak {c}(x,y)$. Combining this and (76) with (47) and (60) shows that for every $k\in \{1,2,\dots ,d\}$ with $\{k\}=\{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ it holds that

$$\begin{aligned} u=c\ne \mathfrak {c}(c,v)=\mathfrak {c}(u,v) . \end{aligned}$$

(77)

This and (62) imply that for every $k\in \{1,2,\dots ,d\}$ with $\{k\}=\{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ it holds that

$$\begin{aligned} x_k\ne y_k . \end{aligned}$$

(78)

Combining this with (69) proves that for every $k\in \{1,2,\dots ,d\}$ with $\{k\}=\{l\in \{1,2,\dots ,d\}:c_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ it holds that

$$\begin{aligned} \mathfrak {r}(v)<\mathfrak {r}(y) . \end{aligned}$$

(79)

This, (77), and (78) establish item (iv). The proof of Lemma 2.5 is thus complete. $\square$

Lemma 2.6

Let satisfy for every $k\in \mathbb {N}$, $x\in [-k-\nicefrac 12,-k+\nicefrac 12)$, $y\in [-\nicefrac 12,\nicefrac 12]$, $z\in (k-\nicefrac 12,k+\nicefrac 12]$ that

(80)

let $a\in \mathbb {R}$, $b\in (a,\infty )$, and let $r:\mathbb {R}\rightarrow \mathbb {Z}$ satisfy for every $x\in \mathbb {R}$ that

$$\begin{aligned} r(x) = \big \lceil {\tfrac{x-a}{b-a}-\tfrac{1}{2}}\big \rfloor . \end{aligned}$$

(81)

Then it holds for every $x\in (-\infty ,a)$, $y\in (b,\infty )$ that

$$\begin{aligned} |{r(2a-x)} | = |{r(x)} |-1 \qquad \text {and}\qquad |{r(2b-y)} | = |{r(y)} |-1 . \end{aligned}$$

(82)

Proof of Lemma 2.6

Observe that (80) and the fact that for every $x\in (0,b-a]$ it holds that $k+\tfrac{x}{b-a}-\tfrac{1}{2}\in (k-\tfrac{1}{2},-k+\tfrac{1}{2}]$ ensure that for every $k\in \mathbb {N}$, $x\in (0,b-a]$ it holds that

$$\begin{aligned} r(a+k(b-a)+x) = \big \lceil {k+\tfrac{x}{b-a}-\tfrac{1}{2}}\big \rfloor = k . \end{aligned}$$

(83)

Moreover, note that (80) and the fact that for every $x\in (0,b-a]$ it holds that $-k+\tfrac{1}{2}-\tfrac{x}{b-a}\in [-k-\tfrac{1}{2},-k+\tfrac{1}{2})$ imply that for every $k\in \mathbb {N}$, $x\in (0,b-a]$ it holds that

$$\begin{aligned} r(b-k(b-a)-x) = \big \lceil {1-k-\tfrac{x}{b-a}-\tfrac{1}{2}}\big \rfloor = \big \lceil {-k+\tfrac{1}{2}-\tfrac{x}{b-a}}\big \rfloor = -k . \end{aligned}$$

(84)

Next observe that (83) and (84) show that for every $k\in \mathbb {N}_0$, $x\in (0,b-a]$ it holds that

$$\begin{aligned}{} & {} |{r(2a-(a-k(b-a)-x))} | = |{r(a+k(b-a)+x)} | = |{k} | = k\nonumber \\{} & {} \quad = |{-(k+1)} |-1 = |{r(b-(k+1)(b-a)-x)} |-1 = |{r(a-k(b-a)-x)} |-1 .\nonumber \\ \end{aligned}$$

(85)

This and the fact that for every $x\in (-\infty ,a)$ there exist $k\in \mathbb {N}_0$, $y\in (0,b-a]$ such that $x = a-k(b-a)-y$ prove that for every $x\in (-\infty ,a)$ it holds that

$$\begin{aligned} |{r(2a-x)} | = |{r(x)} |-1 . \end{aligned}$$

(86)

Furthermore, note that (83) and (84) ensure that for every $k\in \mathbb {N}_0$, $x\in (0,b-a]$ it holds that

$$\begin{aligned}{} & {} |{r(2b-(b+k(b-a)+x))} | = |{r(b-k(b-a)-x)} | = |{-k} | = k \nonumber \\{} & {} \quad = |{r(a+(k+1)(b-a)+x)} |-1 = |{r(b+k(b-a)+x)} |-1 .\qquad \quad \end{aligned}$$

(87)

This and the fact that for every $x\in (b,\infty )$ there exist $k\in \mathbb {N}_0$, $y\in (0,b-a]$ such that $x = b+k(b-a)+y$ demonstrate that for every $x\in (b,\infty )$ it holds that

$$\begin{aligned} |{r(2b-x)} | = |{r(x)} |-1 . \end{aligned}$$

(88)

This and (86) establish (82). The proof of Lemma 2.6 is thus complete. $\square$

Corollary 2.7

Let $d\in \mathbb {N}$, for every $k\in \{1,2,\dots ,d\}$ let $\mathfrak {a}_k^0\in \mathbb {R}$, $\mathfrak {a}_k^1\in (\mathfrak {a}_k^0,\infty )$, let $D=[\mathfrak {a}_1^0,\mathfrak {a}_1^1]\times [\mathfrak {a}_2^0,\mathfrak {a}_2^1]\times \cdots \times [\mathfrak {a}_d^0,\mathfrak {a}_d^1]\subseteq \mathbb {R}^d$, let $e_1=(1,0,0,\dots ,0)$, $e_2=(0,1,0,\dots ,0)$, $\dots$, $e_d=(0,\dots ,0,0,1)\in \mathbb {R}^d$, let $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$ satisfy for every $x=(x_1,\dots ,x_d)\in \partial _D$, $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:x_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

$$\begin{aligned} \begin{aligned} \textbf{n}(x) = {\left\{ \begin{array}{ll} -e_k&{}:x_k=\mathfrak {a}_k^0\\ e_k&{}:x_k=\mathfrak {a}_k^1, \end{array}\right. } \end{aligned} \end{aligned}$$

(89)

let $\mathfrak {c}:(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(90)

let $\mathscr {R}:(\mathbb {R}^d)^2\rightarrow (\mathbb {R}^d)^2$ satisfy for every $x,y\in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\textbf{n}(\mathfrak {c}(x,y))}\big \rangle \textbf{n}(\mathfrak {c}(x,y)) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x, y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(91)

let $x_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, and $y_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, satisfy for every $n\in \mathbb {N}$ that

$$\begin{aligned} x_0\in D \qquad \text {and}\qquad (x_{n},y_{n}) = \mathscr {R}(x_{n-1},y_{n-1}) , \end{aligned}$$

(92)

and let $N\in \mathbb {N}\cup \{\infty \}$ satisfy

$$\begin{aligned} N = \min (\{n\in \mathbb {N}:\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}\}\cup \{\infty \}) \end{aligned}$$

(93)

(cf. Lemma 2.1). Then

• (i) it holds that $N<\infty$ and

• (ii) it holds for every $n\in \mathbb {N}\cap [N,\infty )$ that $(x_n,y_n) = (x_N,y_N)$.

Proof of Corollary 2.7

Throughout this proof let satisfy for every $k\in \mathbb {N}$, $u\in [-k-\nicefrac 12,-k+\nicefrac 12)$, $v\in [-\nicefrac 12,\nicefrac 12]$, $w\in (k-\nicefrac 12,k+\nicefrac 12]$ that

(94)

for every $a\in \mathbb {R}$, $b\in (a,\infty )$ let $r_{a,b}:\mathbb {R}\rightarrow \mathbb {Z}$ satisfy for every $z\in \mathbb {R}$ that

$$\begin{aligned} r_{a,b}(z) = \big \lceil {\tfrac{z-a}{b-a}-\tfrac{1}{2}}\big \rfloor , \end{aligned}$$

(95)

and let $\mathfrak r:\mathbb {R}^d\rightarrow \mathbb {N}_0$ satisfy for every $z=(z_1,\dots ,z_d)\in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak r(z) = \sum _{k=1}^{d} |{r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(z_k)} | . \end{aligned}$$

(96)

Observe that Lemma 2.6 shows that for every $a,b,w,z\in \mathbb {R}$ with $w<a<b<z$ it holds that

$$\begin{aligned} |{r_{a,b}(2a-w)} |< |{r_{a,b}(w)} | \qquad \text {and}\qquad |{r_{a,b}(2b-z)} | < |{r_{a,b}(z)} |. \end{aligned}$$

(97)

Item (iii) in Lemma 2.5 and (92) therefore establish that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ and $\mathfrak {c}(x_n,y_n)\notin \{x_n,y_n\}$ it holds that

$$\begin{aligned} \mathfrak {r}(y_n)<\mathfrak {r}(y_{n-1}) . \end{aligned}$$

(98)

The fact that for every $z\in \mathbb {R}^d$ it holds that $\mathfrak {r}(z)\in \mathbb {N}_0$ and (93) hence imply that

$$\begin{aligned} N < \infty . \end{aligned}$$

(99)

Moreover, note that item (iii) in Lemma 2.3 ensures that for every $n\in \mathbb {N}\cap [N,\infty )$ it holds that

$$\begin{aligned} (x_n,y_n) = (x_N,y_N) . \end{aligned}$$

(100)

The proof of Corollary 2.7 is thus complete.

Lemma 2.8

Let $\lfloor {\cdot } \rfloor :\mathbb {R}\rightarrow \mathbb {Z}$ satisfy for every $k\in \mathbb {Z}$, $x\in [k,k+1)$ that

$$\begin{aligned} \lfloor {x} \rfloor = k, \end{aligned}$$

(101)

let $a\in \mathbb {R}$, $b\in (a,\infty )$, and let $\mathscr {R}:\mathbb {R}\rightarrow [0,1]$ and $\mathscr {S}:\mathbb {R}\rightarrow [a,b]$ satisfy for every $x\in \mathbb {R}$ that

$$\begin{aligned} \mathscr {R}(x) = {\left\{ \begin{array}{ll} x-\lfloor {x} \rfloor &{}:\lfloor {x} \rfloor \in \{2n:n\in \mathbb {Z}\} \\ \lfloor {x} \rfloor - x+1&{}:\lfloor {x} \rfloor \in \{2n+1:n\in \mathbb {Z}\} \end{array}\right. } \quad \text {and}\quad \mathscr {S}(x) = (b-a)\mathscr {R}\big (\tfrac{x-a}{b-a}\big ) + a . \end{aligned}$$

(102)

Then

• (i) it holds for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ that

  $$\begin{aligned} \mathscr {S}(a+2k(b-a)+x) = a+x = \mathscr {S}(b-(2k+1)(b-a)-x) \end{aligned}$$

  (103)

  and

• (ii) it holds for every $x\in \mathbb {R}$ that $\mathscr {S}(2a-x) = \mathscr {S}(x) = \mathscr {S}(2b-x)$.

Proof of Lemma 2.8

First, observe that (101) and (102) imply that for every $k\in \mathbb {Z}$, $x\in [0,1)$ it holds that

$$\begin{aligned} \mathscr {R}(2k+x) = (2k+x)-2k = x . \end{aligned}$$

(104)

Combining this with (102) shows that for every $k\in \mathbb {Z}$, $x\in [0,b-a)$ it holds that

$$\begin{aligned} \mathscr {S}(a+2k(b-a)+x) = (b-a)\mathscr {R}\big ({2k+\tfrac{x}{b-a}}\big )+a = a+x . \end{aligned}$$

(105)

Furthermore, note that (101) and (102) ensure that for every $k\in \mathbb {Z}$, $x\in [0,1)$ it holds that

$$\begin{aligned} \mathscr {R}(2k+1+x) = 2k+1-(2k+1+x)+1 = 1-x . \end{aligned}$$

(106)

This and (102) imply that for every $k\in \mathbb {Z}$ it holds that

$$\begin{aligned} \mathscr {S}(a+2k(b-a)+(b-a)) = (b-a)\mathscr {R}(2k+1)+a = a+(b-a) . \end{aligned}$$

(107)

Combining this with (105) shows that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(a+2k(b-a)+x) = a+x . \end{aligned}$$

(108)

Next observe that (106) and (102) prove that for every $k\in \mathbb {Z}$, $x\in (0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(b-(2k+1)(b-a)-x)= & {} (b-a)\mathscr {R}\big ({1-(2k+1)-\tfrac{x}{b-a}}\big )+a\nonumber \\= & {} (b-a)\mathscr {R}\big ({2(-k-1)+1+\big ({1-\tfrac{x}{b-a}}\big )}\big )+a\nonumber \\= & {} (b-a)\big ({1-\big ({1-\tfrac{x}{b-a}}\big )}\big )+a\nonumber \\= & {} a+x . \end{aligned}$$

(109)

Moreover, note that (104) and (102) imply that for every $k\in \mathbb {Z}$ it holds that

$$\begin{aligned} \mathscr {S}(b-(2k+1)(b-a)) = (b-a)\mathscr {R}(1-(2k+1) )+a = (b-a)\mathscr {R}(-2k )+a = a . \end{aligned}$$

(110)

Combining this with (109) demonstrates that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(b-(2k+1)(b-a)-x) = a+x . \end{aligned}$$

(111)

This and (108) establish item (i). In the next step we observe that item (i) shows that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(2a-(a+2k(b-a)+x))= & {} \mathscr {S}(b-(2k+1)(b-a)-x) \nonumber \\= & {} a+x = \mathscr {S}(a+2k(b-a)+x) . \end{aligned}$$

(112)

Furthermore, note that item (i) ensures that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(2a-(b-(2k+1)(b-a)-x))= & {} \mathscr {S}(a+2k(b-a)+x) \nonumber \\= & {} a+x = \mathscr {S}(b-(2k+1)(b-a)-x) . \end{aligned}$$

(113)

Moreover, observe that item (i) implies that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(2b-(a+2k(b-a)+x))= & {} \mathscr {S}(b-(2k-1)(b-a)-x)\nonumber \\= & {} a+x = \mathscr {S}(a+2k(b-a)+x) . \end{aligned}$$

(114)

In addition, note that item (i) shows that for every $k\in \mathbb {Z}$, $x\in [0,b-a]$ it holds that

$$\begin{aligned} \mathscr {S}(2b-(b-(2k+1)(b-a)-x))= & {} \mathscr {S}(a+(2k+2)(b-a)+x) \nonumber \\= & {} a+x = \mathscr {S}(b-(2k+1)(b-a)-x) .\qquad \quad \end{aligned}$$

(115)

Combining this, (112), (113), and (114) with the fact that for every $y\in \mathbb {R}$ there exist $k\in \mathbb {Z}$, $x\in [0,b-a]$ such that $y\in \{a+2k(b-a)+x,b-(2k+1)(b-a)-x\}$ establishes item (ii). The proof of Lemma 2.8 is thus complete. $\square$

Corollary 2.9

Let $d\in \mathbb {N}$, for every $k\in \{1,2,\dots ,d\}$ let $\mathfrak {a}_k^0\in \mathbb {R}$, $\mathfrak {a}_k^1\in (\mathfrak {a}_k^0,\infty )$, let $D=[\mathfrak {a}_1^0,\mathfrak {a}_1^1]\times [\mathfrak {a}_2^0,\mathfrak {a}_2^1]\times \cdots \times [\mathfrak {a}_d^0,\mathfrak {a}_d^1]\subseteq \mathbb {R}^d$, let $e_1=(1,0,0,\dots ,0)$, $e_2=(0,1,0,\dots ,0)$, $\dots$, $e_d=(0,\dots ,0,0,1)\in \mathbb {R}^d$, let $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$ satisfy for every $x=(x_1,\dots ,x_d)\in \partial _D$, $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:x_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

$$\begin{aligned} \begin{aligned} \textbf{n}(x) = {\left\{ \begin{array}{ll} -e_k&{}:x_k=\mathfrak {a}_k^0\\ e_k&{}:x_k=\mathfrak {a}_k^1, \end{array}\right. } \end{aligned} \end{aligned}$$

(116)

let $\mathfrak {c}:(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(117)

let $\mathscr {R}:(\mathbb {R}^d)^2\rightarrow (\mathbb {R}^d)^2$ satisfy for every $x,y\in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\textbf{n}(\mathfrak {c}(x,y))}\big \rangle \textbf{n}(\mathfrak {c}(x,y)) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x, y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(118)

let $\lfloor {\cdot } \rfloor :\mathbb {R}\rightarrow \mathbb {Z}$ satisfy for every $k\in \mathbb {Z}$, $z\in [k,k+1)$ that $\lfloor {z} \rfloor = k$, let $\mathfrak {r}:\mathbb {R}\rightarrow [0,1]$ satisfy for every $z\in \mathbb {R}$ that

$$\begin{aligned} \mathfrak {r}(x) = {\left\{ \begin{array}{ll} z-\lfloor {z} \rfloor &{}:\lfloor {z} \rfloor \in \{2n:n\in \mathbb {Z}\} \\ \lfloor {z} \rfloor - z+1&{}:\lfloor {z} \rfloor \in \{2n+1:n\in \mathbb {Z}\}, \end{array}\right. } \end{aligned}$$

(119)

for every $a,b\in \mathbb {R}$ let $\,r_{a, b}:\mathbb {R}\rightarrow [a,b]$ satisfy for every $z\in \mathbb {R}$ that $\,{r_{a, b}}(z) = (b-a)\mathfrak {r}\big ({\tfrac{z-a}{b-a}}\big ) + a$, let $\mathscr {S}:\mathbb {R}^d\rightarrow D$ satisfy for every $z=(z_1,\dots ,z_d)\in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {S}(z) = \big (r_{\mathfrak {a}_1^0,\mathfrak {a}_1^1}(z_1),r_{\mathfrak {a}_2^0,\mathfrak {a}_2^1}(z_2),\dots ,r_{\mathfrak {a}_d^0,\mathfrak {a}_d^1}(z_d)\big ) , \end{aligned}$$

(120)

let $x_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, and $y_n\in \mathbb {R}^d$, $n\in \mathbb {N}_0$, satisfy for every $n\in \mathbb {N}$ that

$$\begin{aligned} x_0\in D\backslash \partial _D \qquad \text {and}\qquad (x_n,y_n) = \mathscr {R}(x_{n-1},y_{n-1}), \end{aligned}$$

(121)

and assume for every $n\in \mathbb {N}$ that

$$\begin{aligned} \mathfrak {c}(x_n,y_n) \notin \{z=(z_1,\dots ,z_d)\in \mathbb {R}^d:|{\{k\in \{1,2,\dots ,d\}:z_k\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}\}} |>1\} \end{aligned}$$

(122)

(cf. Lemma 2.1). Then there exists $N\in \mathbb {N}$ such that for every $n\in \mathbb {N}\cap [N,\infty )$ it holds that

$$\begin{aligned} y_n = \mathscr {S}(y_0) . \end{aligned}$$

(123)

Proof of Corollary 2.9

Throughout this proof let $N\in \mathbb {N}\cup \{\infty \}$ satisfy

$$\begin{aligned} N = \min (\{n\in \mathbb {N}:\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}\}\cup \{\infty \}) . \end{aligned}$$

(124)

Note that Corollary 2.7 proves that

• (A) it holds that $N<\infty$ and

• (B) it holds for every $n\in \mathbb {N}\cap [N,\infty )$ that $(x_n,y_n)=(x_N,y_N)$.

Observe that Lemma 2.1 and (122) ensure that for every $n\in \mathbb {N}_0$ with $\mathfrak {c}(x_{n},y_{n})\notin \{x_{n},y_{n}\}$ it holds that

$$\begin{aligned} \mathfrak {c}(x_n,y_n) \in \{z=(z_1,\dots ,z_d)\in \mathbb {R}^d:|{\{k\in \{1,2,\dots ,d\}:z_k\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\}\}} |=1\} . \end{aligned}$$

(125)

Item (iv) in Lemma 2.5 therefore establishes that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that

$$\begin{aligned} \mathfrak {c}(x_n,y_n) \ne x_n . \end{aligned}$$

(126)

Furthermore, note that the assumption that $x\in D\backslash \partial _D$ and (117) imply that

$$\begin{aligned} \mathfrak {c}(x_0,y_0) \ne x_0 . \end{aligned}$$

(127)

Combining this and (126) with (124) and item (A) shows that

$$\begin{aligned} \mathfrak {c}(x_{N-1},y_{N-1}) = y_{N-1} . \end{aligned}$$

(128)

The fact that D is a closed set and (117) therefore demonstrate that $y_{N-1}\in D$. This, (118), and items (A) and (B) prove that for every $n\in \mathbb {N}\cap [N,\infty )$ it holds that

$$\begin{aligned} y_n = y_N = y_{N-1} \in D . \end{aligned}$$

(129)

In the next step we observe that item (ii) in Lemma 2.8 establishes that for every $k\in \{1,2,\dots ,d\}$, $z\in \mathbb {R}$ it holds that

$$\begin{aligned} r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(2\mathfrak {a}_k^0 - z) = r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(z) \qquad \text {and}\qquad r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(2\mathfrak {a}_k^1 - z) = r_{\mathfrak {a}_k^0,\mathfrak {a}_k^1}(z) . \end{aligned}$$

(130)

Item (ii) in Lemma 2.5 and (121) therefore imply that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\notin \{x_{n-1},y_{n-1}\}$ it holds that $\mathscr {S}(y_n) = \mathscr {S}(y_{n-1})$. Combining this and the fact that for every $n\in \mathbb {N}$ with $\mathfrak {c}(x_{n-1},y_{n-1})\in \{x_{n-1},y_{n-1}\}$ it holds that $y_n=y_{n-1}$ with induction demonstrates that for every $n\in \mathbb {N}$ it holds that

$$\begin{aligned} \mathscr {S}(y_n) = \mathscr {S}(y_0) . \end{aligned}$$

(131)

In addition, note that item (i) in Lemma 2.8 ensures that for every $a\in \mathbb {R}$, $b\in (a,\infty )$, $z\in [a,b]$ it holds that $\,{r_{a, b}}(z) = z$. Hence, we obtain that for every $z\in D$ it holds that

$$\begin{aligned} \mathscr {S}(z) = z. \end{aligned}$$

(132)

Combining this with (129) and (131) establishes that for every $n\in \mathbb {N}\cap [N,\infty )$ it holds that

$$\begin{aligned} y_n = \mathscr {S}(y_n) = \mathscr {S}(y_0) . \end{aligned}$$

(133)

The proof of Corollary 2.9 is thus complete. $\square$

Framework 2.10

(Reflection principle for the simulation of time discrete reflected processes) Let $d \in \mathbb {N}$, let $D\subseteq \mathbb {R}^{ d }$ be a sufficiently regular closed set, let $\textbf{n} :\partial _D\rightarrow \mathbb {R}^d$ be a suitable outer unit normal vector field associated to $D$, let $\mathfrak {c} :(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathfrak {c}(x,y) = x + \big [{\inf ( \{r \in [0,1] :x + r(y - x) \notin D\}\cup \{1\})}\big ] (y-x) , \end{aligned}$$

(134)

let $\mathscr {R} :(\mathbb {R}^{ d })^2 \rightarrow ( \mathbb {R}^{ d })^2$ satisfy for every $x,y \in \mathbb {R}^d$ that

$$\begin{aligned} \mathscr {R}(x,y) = {\left\{ \begin{array}{ll} (x,y) &{} :\mathfrak {c}(x,y) =x \\ \big ({ \mathfrak {c}(x,y), y - 2 \big \langle { y-\mathfrak {c}(x,y),\textbf{n}(\mathfrak {c}(x,y))}\big \rangle \textbf{n}(\mathfrak {c}(x,y)) }\big ) &{} :\mathfrak {c}(x,y) \notin \{x,y\} \\ (y,y) &{} :\mathfrak {c}(x,y) = y, \end{array}\right. } \end{aligned}$$

(135)

let $P :(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y \in \mathbb {R}^d$ that $P(x,y) = y$, let $\mathcal {R}_{n} :(\mathbb {R}^d)^2 \rightarrow ( \mathbb {R}^{ d } )^2$, $n \in \mathbb {N}_0$, satisfy for every $n \in \mathbb {N}_0$, $x,y \in \mathbb {R}^d$ that $\mathcal {R}_0(x,y) = (x,y)$ and $\mathcal {R}_{ n + 1 }(x,y) = \mathscr {R}( \mathcal {R}_{n} (x,y ) )$, and let $R :(\mathbb {R}^d)^2 \rightarrow \mathbb {R}^d$ satisfy for every $x,y\in \mathbb {R}^d$ that

$$\begin{aligned} R(x,y) = {\textstyle \lim _{n\rightarrow \infty }} P(\mathcal {R}_{n}(x,y)) \end{aligned}$$

(136)

(cf. Lemma 2.1).

Note that in Framework 2.10 above, for every $d\in \mathbb {N}$, every closed set $D\subseteq \mathbb {R}^d$ with a smooth boundary $\partial _D$, every suitable outer unit normal vector field $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$, and every $a\in D\backslash \partial _D$, $b\in \mathbb {R}^d\backslash D$ we have

• (i) that $\mathfrak c(a,b)$ is the point closest to a on the line segment from a to b which lies on $\partial _D$ and

• (ii) that $\mathscr {R}(a,b)$ is the reflection of b on the hyperplane through $\mathfrak c(a,b)$ tangent to $\partial _D$ (cf. Fig. 1).

In view of this, we can, roughly speaking, think of R(a, b) as the point where a particle that travels a length of $\Vert {b-a} \Vert$ starting in a going towards b and getting reflected every time it hits the boundary of D, ends up; cf. Fig. 1.

Fig. 1

Two illustrations for Framework 2.10. The diagram on the left shows the reflection of a line segment from a to b on a hyperplane with unit normal vector n. The diagram on the right illustrates the recursive definition of the functions $\mathcal R_n:(\mathbb {R}^d)^2\rightarrow (\mathbb {R}^d)^2$, $n\in \mathbb {N}_0$, and $R:(\mathbb {R}^d)^2\rightarrow \mathbb {R}$ defined in Framework 2.10 in the case where $d=2$ and $D\subseteq \mathbb {R}^d$ is a closed rectangle

Also, observe that in Framework 2.10 above, we have used the vague notions of “sufficiently regular set” and “suitable outer unit normal vector field”. Corollaries 2.7 and 2.9 and Proposition 2.4 above provide more information on two particular special cases of the construction in Framework 2.10. More specifically, we consider the conditions satisfied in (at least) the following two cases:

• (a) The case where $D=\{x\in \mathbb {R}^d:\Vert {x} \Vert = 1\}$ and where $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$ satisfies for every $x\in \partial _D=\{x\in \mathbb {R}^d:\Vert {x} \Vert =1\}$ that $\textbf{n}(x) = x$. Note that in this case, Proposition 2.4 demonstrates that the limit in (136) exists.

• (b) The case where for every $k\in \{1,2,\dots ,d\}$ there exist $\mathfrak {a}_k^0\in \mathbb {R}$, $\mathfrak {a}_k^1\in (\mathfrak {a}_k^0,\infty )$ such that $D=[\mathfrak {a}_1^0,\mathfrak {a}_1^1]\times [\mathfrak {a}_2^0,\mathfrak {a}_2^1]\times \cdots \times [\mathfrak {a}_d^0,\mathfrak {a}_d^1]$, where $e_1=(1,0,0,\dots ,0)$, $e_2=(0,1,0,\dots ,0)$, $\dots$, $e_d=(0,\dots ,0,0,1)\in \mathbb {R}^d$, and where $\textbf{n}:\partial _D\rightarrow \mathbb {R}^d$, satisfies for every $x=(x_1,\dots ,x_d)\in \partial _D=\{x=(x_1,\dots ,x_d)\in D:(\exists \, k\in \{1,2,\dots ,d\}:x_k\in \{\mathfrak {a}_k^0,\mathfrak {a}_k^1\})\}$, $k\in \{1,2,\dots ,d\}$ with $k=\min \{l\in \{1,2,\dots ,d\}:x_l\in \{\mathfrak {a}_l^0,\mathfrak {a}_l^1\}\}$ that

  $$\begin{aligned} \begin{aligned} \textbf{n}(x) = {\left\{ \begin{array}{ll} -e_k&{}:x_k=\mathfrak {a}_k^0\\ e_k&{}:x_k=\mathfrak {a}_k^1. \end{array}\right. } \end{aligned} \end{aligned}$$

  (137)

  Note that in this case, Corollary 2.7 demonstrates that the limit in (136) exists and Corollary 2.9 shows how the function R can be practically computed (up to a zero set).

2.3 Description of the proposed approximation method in a special case

Framework 2.11

(Special case of the machine learning-based approximation method) Assume Framework 2.10, let $T,\gamma \in (0,\infty )$, $N,M,K \in \mathbb {N}$, $g \in C^2(\mathbb {R}^d,\mathbb {R})$, $\mathfrak d,\mathfrak {h} \in \mathbb {N}\backslash \{1\}$, $t_0,t_1,\ldots ,t_N\in [0,T]$ satisfy $\mathfrak {d} = \mathfrak {h}(N+1)d(d+1)$ and

$$\begin{aligned} 0 = t_0< t_1< \cdots < t_N = T , \end{aligned}$$

(138)

let $\tau _0, \tau _1, \dots ,\tau _N \in [0,T]$ satisfy for every $n \in \{0,1,\dots ,N\}$ that $\tau _n= T-t_{N-n}$, let $f :\mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ be measurable, let $(\Omega ,{\mathcal {F}},\mathbb {P},(\mathcal {F}_t)_{t\in [0,T]})$ be a filtered probability space, let $\xi ^{m}:\Omega \rightarrow \mathbb {R}^d$, $m\in \mathbb {N}$, be i.i.d. $\mathcal {F}_0$/$\mathcal {B}(\mathbb {R}^d)$-measurable random variables, let $W^{m}:[0,T]\times \Omega \rightarrow \mathbb {R}^d$, $m\in \mathbb {N}$, be i.i.d. standard $(\mathcal {F}_t)_{t\in [0,T]}$-Brownian motions, for every $m\in \mathbb {N}$ let $\mathcal {Y}^{m}:\{0,1,\ldots ,N\}\times \Omega \rightarrow \mathbb {R}^d$ be the stochastic process which satisfies for every $n\in \{0,1,\ldots ,N-1\}$ that $\mathcal {Y}^{m}_0 = \xi ^{m}$ and

$$\begin{aligned} \mathcal {Y}^{m}_{n+1} = R\big ({\mathcal {Y}^{m}_{n}, \mathcal {Y}^{m}_{n} + \sqrt{2} (W^{m}_{\tau _{n+1}}-W^{m}_{\tau _{n}})}\big ) , \end{aligned}$$

(139)

let $\mathcal {L} :\mathbb {R}^d \rightarrow \mathbb {R}^d$ satisfy for every $x = ( x_1, \dots , x_d ) \in \mathbb {R}^d$ that

$$\begin{aligned} \mathcal {L}( x ) = \bigg (\frac{\exp (x_1)}{\exp (x_1)+1},\dots ,\frac{\exp (x_d)}{\exp (x_d)+1}\bigg ), \end{aligned}$$

(140)

for every $\theta = ( \theta _1, \dots , \theta _{ \mathfrak {d} } ) \in \mathbb {R}^{ \mathfrak {d} }$, $k, l, v \in \mathbb {N}$ with $v + l (k + 1 ) \le \mathfrak {d}$ let $A^{ \theta , v }_{ k, l } :\mathbb {R}^k \rightarrow \mathbb {R}^l$ satisfy for every $x = ( x_1, \dots , x_k )\in \mathbb {R}^k$ that

$$\begin{aligned} A^{ \theta , v }_{ k, l }( x ) = \bigg ({ \theta _{v+kl+1}+ \left[ {\textstyle \sum \limits _{i=1}^ k x_i\, \theta _{v+i}}\right] , \dots , \theta _{v+kl+l} + \left[ {\textstyle \sum \limits _{i=1}^ k x_i\, \theta _{v+(l-1)k+i}}\right] }\bigg ) , \end{aligned}$$

(141)

let ${\mathbb {V}}_n:\mathbb {R}^{\mathfrak {d}}\times \mathbb {R}^d\rightarrow \mathbb {R}$, $n\in \{0,1,\ldots ,N\}$, satisfy for every $n\in \{1,2,\ldots ,N\}$, $\theta \in \mathbb {R}^{\mathfrak {d}}$, $x \in \mathbb {R}^d$ that ${\mathbb {V}}_0(\theta ,x) = g(x)$ and

$$\begin{aligned}&{\mathbb {V}}_{ n }(\theta ,x) = \nonumber \\&\big ({A^{ \theta , (\mathfrak {h}n+\mathfrak {h}-1)d(d+1) }_{ d, 1 } \circ \mathcal {L} \circ A^{ \theta , (\mathfrak {h}n+\mathfrak {h}-2)d(d+1) }_{ d, d } \circ \cdots \circ \mathcal {L} \circ A^{ \theta , (\mathfrak {h}n+1)d(d+1) }_{ d, d } \circ \mathcal {L} \circ A^{ \theta , \mathfrak {h}nd(d+1) }_{ d, d }}\big )(x) , \end{aligned}$$

(142)

let $\nu _x :\mathcal {B}( D)\rightarrow [0,1]$, $x \in D$, be probability measures, for every $x \in D$ let $Z^{ n, m }_{ x, k } :\Omega \rightarrow D$, $k, n, m \in \mathbb {N}$, be i.i.d. random variables which satisfy for every $A \in \mathcal {B}( D)$ that $\mathbb {P}( Z_{ x, 1 }^{ 1, 1 } \in A ) = \nu _x( A )$, let $\Theta ^{n}:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\mathfrak {d}}$, $n \in \{0,1,\ldots ,N\}$, be stochastic processes, for every $n \in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$ let $\phi ^{n,m}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}$ satisfy for every $\theta \in \mathbb {R}^{\mathfrak {d}}$, $\omega \in \Omega$ that

$$\begin{aligned} \begin{aligned}&\phi ^{n,m}(\theta ,\omega ) = \left[ {\mathbb {V}}_n\big ({\theta ,\mathcal {Y}^{m}_{N-n}(\omega )}\big ) - {\mathbb {V}}_{n-1}\big ({\Theta ^{n-1}_M(\omega ),\mathcal {Y}^{m}_{N-n+1}(\omega )}\big )\right. \\&\left. \quad - \tfrac{(t_{n}-t_{n-1})}{K} \left[ {\textstyle \sum \limits _{k=1}^{K} f\big ({{\mathbb {V}}_{n-1}(\Theta ^{n-1}_M(\omega ),\mathcal {Y}^{m}_{N-n+1}(\omega )),{\mathbb {V}}_{n-1}(\Theta ^{n-1}_M(\omega ),Z_{ \mathcal {Y}^m_{ N - n + 1 }(\omega ), k }^{ n, m }(\omega )) }\big ) }\right] \right] ^{2}, \end{aligned}\nonumber \\ \end{aligned}$$

(143)

for every $n\in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$ let $\Phi ^{n,m}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}^{\mathfrak {d}}$ satisfy for every $\theta \in \mathbb {R}^{\mathfrak {d}}$, $\omega \in \Omega$ that $\Phi ^{n,m}(\theta ,\omega ) = (\nabla _{\theta }\phi ^{n,m})(\theta ,\omega )$, and assume for every $n\in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$ that

$$\begin{aligned} \Theta ^{n}_{m} = \Theta ^{n}_{m-1} - \gamma \,\Phi ^{n,m}(\Theta ^{n}_{m-1}) . \end{aligned}$$

(144)

As indicated in Sect. 2.1 above, the algorithm described in Framework 2.11 computes an approximation for a solution of the PDE in (1), i.e., a function $u\in C^{1,2}([0,T]\times D,\mathbb {R})$ which has at most polynomially growing derivatives, which satisfies for every $t\in (0,T]$, $x\in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and which satisfies for every $t\in [0,T]$, $x\in D$ that $u(0,x)=g(x)$, $\int _D|{f(u(t,x), u(t,\textbf{x})) } | \, \nu _x(\textrm{d}\textbf{x}) < \infty$, and

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x)&= (\Delta _x u)(t,x) + \int _{D} f(u(t,x),u(t,\textbf{x})) \, \nu _x(\textrm{d}\textbf{x}). \end{aligned} \end{aligned}$$

(145)

Let us now add some explanatory comments on the objects and notations employed in Framework 2.11 above. The algorithm in Framework 2.11 decomposes the time interval [0, T] into N subintervals at the times $t_0,t_1,t_2,\dots ,t_{N}\in [0,T]$ (cf. (138)). For every $n\in \{1,2,\dots ,N\}$ we aim to approximate the function $\mathbb {R}^d\ni x\mapsto u(t_n,x)\in \mathbb {R}$ by a suitable (realization function of a) fully-connected feedforward neural network. Each of these neural networks is an alternating composition of $\mathfrak h-1$ affine linear functions from $\mathbb {R}^d$ to $\mathbb {R}^d$ (where we think of $\mathfrak h\in \mathbb {N}\backslash \{1\}$ as the length or depth of the neural network), of $\mathfrak h-1$ instances of a d-dimensional version of the standard logistic function, and finally of an affine linear function from $\mathbb {R}^d$ to $\mathbb {R}$. Every such neural network can be specified by means of $(\mathfrak h-1)(d^2+d)+d+1\le \mathfrak hd(d+1)$ real parameters and so $N+1$ of these neural networks can be specified by a parameter vector of length $\mathfrak d=\mathfrak h(N+1)d(d+1)\in \mathbb {N}$. Note that $\mathcal L:\mathbb {R}^d\rightarrow \mathbb {R}^d$ in Framework 2.11 above denotes the d-dimensional version of the standard logistic function (cf. (140)) and for every $k,l,v\in \mathbb {N}$, $\theta =(\theta _1,\dots ,\theta _{\mathfrak d})\in \mathbb {R}^{\mathfrak d}$ with $v+kl+l\le \mathfrak d$ the function $A^{\theta ,v}_{k,l}:\mathbb {R}^k\rightarrow \mathbb {R}^l$ in Framework 2.11 denotes an affine linear function specified by means of the parameters $\theta _{v+1},\theta _{v+2},\dots ,\theta _{v+kl+l}$ (cf. (141)). Furthermore, observe that for every $n\in \{1,2,\dots ,N\}$, $\theta \in \mathbb {R}^{\mathfrak d}$ the function

$$\begin{aligned} \mathbb {R}^d\ni x\mapsto \mathbb V_n(\theta ,x)\in \mathbb {R}\end{aligned}$$

(146)

denotes a neural network specified by means of the parameters $\mathfrak {h}nd(d+1)+1, \mathfrak {h}nd(d+1)+2,\dots ,(\mathfrak {h}n+\mathfrak {h}-1)d(d+1)+d+1$.

The goal of the optimization algorithm in Framework 2.11 above is to find a suitable parameter vector $\theta \in \mathbb {R}^{\mathfrak {d}}$ such that for every $n\in \{1,2,\dots ,N\}$ the neural network $\mathbb {R}^d\ni x\mapsto \mathbb {V}_n(\theta ,x)\in \mathbb {R}$ is a good approximation for the solution $\mathbb {R}^d\ni x\mapsto u(t_n,x)\in \mathbb {R}$ to the PDE in (145) at time $t_n$. This is done by performing successively for each $n\in \{1,2,\dots ,N\}$ a plain vanilla stochastic gradient descent (SGD) optimization on a suitable loss function (cf. (144)).

Observe that for every $n\in \{1,2,\dots ,N\}$ the stochastic process $\Theta ^n:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\mathfrak {d}}$ describes the successive estimates computed by the SGD algorithm for the parameter vector that represents (via $\mathbb {V}_n:\mathbb {R}^{\mathfrak {d}}\times \mathbb {R}^d\rightarrow \mathbb {R}$) a suitable approximation to the solution $\mathbb {R}^d\ni x\mapsto u(t_n,x)\in \mathbb {R}$ of the PDE in (145) at time $t_n$. Next note that $M\in \mathbb {N}$ in Framework 2.11 above denotes the number of gradient descent steps taken for each $n\in \{1,2,\dots ,N\}$ and that $\gamma \in (0,\infty )$ denotes the learning rate employed in the SGD algorithm. Moreover, observe that for every $n\in \{1,2,\dots ,N\}$, $m\in \{1,2,\dots ,M\}$ the function $\phi ^{n,m}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}$ denotes the loss function employed in the $m\hbox {th}$ gradient descent step during the approximation of the solution of the PDE in (145) at time $t_n$ (cf. (143)). The loss functions employ a family of i.i.d. time-discrete stochastic processes $\mathcal Y^m:\{0,1,\dots N\}\times \Omega \rightarrow \mathbb {R}^d$, $m\in \mathbb {N}$, which we think of as discretizations of suitable reflected Brownian motions (cf. (139)). In addition, for every $n\in \{1,2,\dots ,N\}$, $m\in \{1,2,\dots ,M\}$, $x\in D$ the loss function $\phi ^{n,m}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}$ employs a family of i.i.d. random variables $Z^{n,m}_{x,k}:\Omega \rightarrow D$, $k\in \mathbb {N}$, which are used for the Monte Carlo approximation of the non-local term in the PDE in (145) whose solution we are trying to approximate. The number of samples used in these Monte Carlo approximations is denoted by $K\in \mathbb {N}$ in Framework 2.11 above.

Finally, for sufficiently large $N,M,K\in \mathbb {N}$ and sufficiently small $\gamma \in (0,\infty )$ the algorithm in Framework 2.11 above yields for every $n\in \{1,2,\dots ,N\}$ a (random) parameter vector $\Theta ^n_M:\Omega \rightarrow \mathbb {R}^{\mathfrak d}$ which represents a function $\mathbb {R}^d\times \Omega \ni (x,\omega )\mapsto \mathbb V_n(\Theta ^n_M(\omega ),x)\in \mathbb {R}$ that we think of as providing for every $x\in D$ a suitable approximation

$$\begin{aligned} \mathbb V_n(\Theta ^n_M,x) \approx u(t_n,x) . \end{aligned}$$

(147)

3 Machine learning-based approximation method in the general case

In this section we describe in Framework 3.1 in Sect. 3.2 below the full version of our deep learning-based method for approximating solutions of non-local nonlinear PDEs with Neumann boundary conditions (see Sect. 3.1 for a description of the class of PDEs our approximation method applies to), which generalizes the algorithm introduced in Framework 2.11 in Sect. 2.3 above and which we apply in Sect. 5 below to several examples of non-local nonlinear PDEs.

3.1 PDEs under consideration

Let $T \in (0,\infty )$, $d \in \mathbb {N}$, let $D\subseteq \mathbb {R}^d$ be a closed set with sufficiently smooth boundary $\partial _D$, let $\textbf{n} :\partial _D\rightarrow \mathbb {R}^d$ be an outer unit normal vector field associated to $D$, let $g:D\rightarrow \mathbb {R}$, $\mu :D\rightarrow \mathbb {R}^d$, and $\sigma :D\rightarrow \mathbb {R}^{ d \times d }$ be continuous, let $\nu _x :\mathcal {B}(D) \rightarrow [0,1]$, $x \in D$, be probability measures, let $f :[0,T] \times D\times D\times \mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ be measurable, let $u= (u(t,x))_{(t,x)\in [0,T]\times D}\in C^{1,2}([0,T]\times D,\mathbb {R})$ have at most polynomially growing partial derivatives, assume for every $t\in [0,T]$, $x\in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$, and assume for every $t\in [0,T]$, $x\in D$ that $u(0,x)=g(x)$, $\int _D\big |{f\big ({t,x,\textbf{x}, u(t,x),u(t,\textbf{x}) }\big ) }\big | \, \nu _x(\textrm{d}\textbf{x}) < \infty$, and

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x)&= \int _{D} f\big ({t,x,\textbf{x}, u(t,x),u(t,\textbf{x}) }\big ) \, \nu _x(\textrm{d}\textbf{x}) \\&\qquad + \big \langle {\mu (x), ( \nabla _x u )( t,x ) }\big \rangle + \tfrac{ 1 }{ 2 } {{\,\textrm{Trace}\,}}\big ({ \sigma (x) [ \sigma (x) ]^* ( {{\,\textrm{Hess}\,}}_x u)( t,x ) }\big ). \end{aligned} \end{aligned}$$

(148)

Our goal is to approximately calculate under suitable hypotheses the solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (148).

3.2 Description of the proposed approximation method in the general case

Framework 3.1

(General case of the machine learning-based approximation method) Assume Framework 2.10, let $T \in (0,\infty )$, $N, \varrho , \mathfrak {d}, \varsigma \in \mathbb {N}$, $(M_n)_{n\in \mathbb {N}_0}\subseteq \mathbb {N}$, $(K_n)_{n\in \mathbb {N}}\subseteq \mathbb {N}$, $(J_m)_{m \in \mathbb {N}} \subseteq \mathbb {N}$, $t_0,t_1,\ldots ,t_N\in [0,T]$ satisfy

$$\begin{aligned} 0 = t_0< t_1< \ldots < t_N = T , \end{aligned}$$

(149)

let $\tau _0, \tau _1, \dots ,\tau _N \in [0,T]$ satisfy for every $n \in \{0, 1, \dots , N\}$ that $\tau _n= T-t_{N-n}$, let $\nu _x :\mathcal {B}( D)\rightarrow [0,1]$, $x \in D$, be probability measures, for every $x \in D$ let $Z^{ n, m,j }_{ x, k } :\Omega \rightarrow D$, $k, n, m, j \in \mathbb {N}$, be i.i.d. random variables which satisfy for every $A \in \mathcal {B}( D)$ that $\mathbb {P}( Z_{ x, 1 }^{ 1, 1,1 } \in A ) = \nu _x( A )$, let $f:[0,T] \times D\times D\times \mathbb {R}\times \mathbb {R}\rightarrow \mathbb {R}$ be measurable, let $( \Omega , {\mathcal {F}}, \mathbb {P}, ( \mathcal {F}_t )_{ t \in [0,T] } )$ be a filtered probability space, for every $n \in \{1,2,\ldots ,N\}$ let $W^{n,m,j} :[0,T] \times \Omega \rightarrow \mathbb {R}^d$, $m,j \in \mathbb {N}$, be i.i.d. standard $( \mathcal {F}_t )_{ t \in [0,T] }$-Brownian motions, for every $n \in \{1, 2, \ldots ,N\}$ let $\xi ^{n,m,j}:\Omega \rightarrow \mathbb {R}^d$, $m, j \in \mathbb {N}$, be i.i.d. $\mathcal {F}_0$/$\mathcal {B}(\mathbb {R}^d)$-measurable random variables, let $H:[0,T]^2\times \mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}^d$ be a function, for every $j\in \mathbb {N}$, $\textbf{s}\in \mathbb {R}^\varsigma$, $n\in \{0, 1, \dots ,N\}$ let ${\mathbb {V}}^{j,\textbf{s}}_n:\mathbb {R}^{\mathfrak {d}}\times \mathbb {R}^d\rightarrow \mathbb {R}$ be a function, for every $n \in \{1,2, \ldots ,N\}$, $m,j \in \mathbb {N}$ let $\mathcal {Y}^{n,m,j}:\{0,1,\ldots ,N\}\times \Omega \rightarrow \mathbb {R}^d$ be a stochastic process which satisfies for every $k\in \{0,1,\ldots ,N-1\}$ that $\mathcal {Y}^{n,m,j}_0 = \xi ^{ n, m, j }$ and

$$\begin{aligned} \mathcal {Y}^{n,m,j}_{k+1} = H\big (\tau _{k+1},\tau _{k},\mathcal {Y}^{n,m,j}_k,W^{n,m,j}_{\tau _{k + 1}} - W^{n,m,j}_{\tau _{k}}\big ) , \end{aligned}$$

(150)

let $\Theta ^{n}:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\mathfrak {d}}$, $n \in \{0, 1, \dots , N\}$, be stochastic processes, for every $n\in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$, $\textbf{s}\in \mathbb {R}^{\varsigma }$ let $\phi ^{n,m,\textbf{s}}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}$ satisfy for every $\theta \in \mathbb {R}^{\mathfrak {d}}$, $\omega \in \Omega$ that

$$\begin{aligned} \begin{aligned} \phi ^{n,m,\textbf{s}}(\theta ,\omega ) =&\frac{1}{J_m}\sum _{j=1}^{J_m} \left[ {\mathbb {V}}^{j,\textbf{s}}_n\big ({\theta ,\mathcal {Y}^{n,m,j}_{N-n}(\omega )}\big )- {\mathbb {V}}^{j,\textbf{s}}_{n-1}\big ({\Theta ^{n-1}_{M_{n-1}}(\omega ), \mathcal {Y}^{n,m,j}_{N-n+1}(\omega )}\big )\right. \\&- \tfrac{(t_n-t_{n-1})}{K_n} \Bigg [ \textstyle \sum \limits _{k=1}^{K_n} f\Big (t_{n-1}, \mathcal {Y}^{n,m,j}_{N-n+1}(\omega ), Z_{ \mathcal {Y}^{n,m,j}_{ N - n + 1 }(\omega ), k }^{ n, m,j }(\omega ),\\&\left. bV^{j,\textbf{s}}_{n-1} \big ({\Theta ^{n-1}_{M_{n-1}}(\omega ),\mathcal {Y}^{n,m,j}_{N-n+1}(\omega )}\big ), {\mathbb {V}}^{j,\textbf{s}}_{n-1}\big ({\Theta ^{n-1}_{M_{n-1}}(\omega ), Z_{ \mathcal {Y}^{n,m,j}_{ N - n + 1 }(\omega ), k }^{ n, m,j }(\omega )}\big ) \Big )\Bigg ] \right] ^2, \end{aligned} \end{aligned}$$

(151)

for every $n\in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$, $\textbf{s}\in \mathbb {R}^{\varsigma }$ let $\Phi ^{n,m,\textbf{s}}:\mathbb {R}^{\mathfrak {d}}\times \Omega \rightarrow \mathbb {R}^{\mathfrak {d}}$ satisfy for every $\omega \in \Omega$, $\theta \in \{\vartheta \in \mathbb {R}^{\mathfrak {d}}:(\mathbb {R}^{\mathfrak d}\ni \eta \mapsto \phi ^{n,m,\textbf{s}}(\eta ,\omega )\in \mathbb {R})$ is differentiable at $\vartheta \}$ that

$$\begin{aligned} \Phi ^{n,m,\textbf{s}}(\theta ,\omega ) = (\nabla _{\theta }\phi ^{n,m,\textbf{s}})(\theta ,\omega ) , \end{aligned}$$

(152)

let $\mathcal {S}^n:\mathbb {R}^{\varsigma }\times \mathbb {R}^{\mathfrak {d}}\times (\mathbb {R}^d)^{\{0,1,\ldots ,N\}\times \mathbb {N}}\rightarrow \mathbb {R}^{\varsigma }$, $n\in \{1,2,\ldots ,N\}$, be functions, for every $n\in \{1,2,\ldots ,N\}$, $m\in \mathbb {N}$ let $\psi ^n_m:\mathbb {R}^{\varrho }\rightarrow \mathbb {R}^{\mathfrak {d}}$ and $\Psi ^n_m:\mathbb {R}^{\varrho }\times \mathbb {R}^{\mathfrak {d}}\rightarrow \mathbb {R}^{\varrho }$ be functions, and for every $n\in \{1,2,\ldots ,N\}$ let $\mathbb {S}^{n}:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\varsigma }$ and $\Xi ^{n}:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\varrho }$ be stochastic processes which satisfy for every $m\in \mathbb {N}$ that

$$\begin{aligned} \mathbb {S}^{n}_{m}= & {} \mathcal {S}^{n}\big ({\mathbb {S}^{n}_{m-1}, \Theta ^{n}_{m-1}, (\mathcal {Y}_k^{n,m,i})_{(k,i)\in \{0,1,\ldots ,N\}\times \mathbb {N}}}\big ) , \end{aligned}$$

(153)

$$\begin{aligned} \Xi ^n_{m}= & {} \Psi ^n_{m}(\Xi ^n_{m-1},\Phi ^{n,m,\mathbb {S}^n_{m}}(\Theta ^n_{m-1})) , \qquad \text {and}\qquad \Theta ^{n}_{m} = \Theta ^{n}_{m-1} - \psi ^n_{m}(\Xi ^n_{m}) . \end{aligned}$$

(154)

In the setting of Framework 3.1 above we think under suitable hypotheses for sufficiently large $N \in \mathbb {N}$, sufficiently large $(M_n)_{n\in \mathbb {N}_0} \subseteq \mathbb {N}$, sufficiently large $(K_n)_{n\in \mathbb {N}} \subseteq \mathbb {N}$, every $n \in \{0, 1, \dots , N\}$, and every $x \in D$ of $\mathbb {V}^{1,\mathbb {S}_{M_n}^n}_n(\Theta ^n_{M_n},x) :\Omega \rightarrow \mathbb {R}$ as a suitable approximation

$$\begin{aligned} \mathbb {V}^{1,\mathbb {S}_{M_n}^n}_n(\Theta ^n_{M_n},x) \approx u(t_n,x) \end{aligned}$$

(155)

of $u(t_n,x)$ where $u=(u(t,x))_{(t,x)\in [0,T]\times \mathbb {R}^d}\in C^{1,2}([0,T]\times \mathbb {R}^d,\mathbb {R})$ is a function with at most polynomially growing derivatives which satisfies for every $t\in (0,T]$, $x\in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and which satisfies for every $t\in [0,T]$, $x\in D$ that $u(0,x)=g(x)$, $\int _D\big |{f\big ({t,x,\textbf{x}, u(t,x), u(t,\textbf{x}) }\big ) }\big | \, \nu _x(\textrm{d}\textbf{x}) < \infty$, and

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x)&= \int _{D} f\big ({t,x,\textbf{x}, u(t,x),u(t,\textbf{x}) }\big ) \, \nu _x(\textrm{d}\textbf{x}) \\&\quad + \big \langle {\mu (x), ( \nabla _x u )( t,x ) }\big \rangle + \tfrac{ 1 }{ 2 } {{\,\textrm{Trace}\,}}\big ({ \sigma (x) [ \sigma (x) ]^* ( {{\,\textrm{Hess}\,}}_x u)( t,x ) }\big ) \end{aligned} \end{aligned}$$

(156)

(cf. (148)). Compared to the simplified algorithm in Framework 2.11 above, the major new elements introduced in Framework 3.1 are the following:

• (a) The numbers of gradient descent steps taken to compute approximations for the solution of the PDE at the times $t_n$, $n\in \{1,2,\dots ,N\}$, are allowed to vary with n, and so are specified by a sequence $(M_n)_{n\in \mathbb {N}_0}\subseteq \mathbb {N}$ in Framework 3.1 above.

• (b) The numbers of samples used for the Monte Carlo approximation of the non-local term in the approximation for the solution of the PDE at the times $t_n$, $n\in \{1,2,\dots ,N\}$, are allowed to vary with n, and so are specified by a sequence $(K_n)_{n\in \mathbb {N}_0}\subseteq \mathbb {N}$ in Framework 3.1 above.

• (c) The approximating functions $\mathbb V^{j,\textbf{s}}_n$, $(j,\textbf{s},n)\in \mathbb {N}\times \mathbb {R}^\varsigma \times \{0,1,\dots ,N\}$, in Framework 3.1 above are not specified concretely in order to allow for a variety of neural network architectures. For the concrete choice of these functions employed in our numerical simulations, we refer the reader to Sect. 5.

• (d) For every $m\in \{1,2,\dots ,M\}$ the loss function used in the $m\hbox {th}$ gradient descent step may be computed using a minibatch of samples instead of just one sample (cf. (151)). The sizes of these minibatches are specified by a sequence $(J_m)_{m\in \mathbb {N}}\subseteq \mathbb {N}$.

• (e) Compared to Framework 2.11 above, the more general form of the PDEs considered in this section (cf. (156)) requires more flexibility in the definition of the time-discrete stochastic processes $\mathcal Y^{n,m,j}:\{0,1,\dots ,N\}\times \Omega \rightarrow \mathbb {R}^d$, $(n,m,j)\in \{1,2,\dots ,N\}\times \mathbb {N}\times \mathbb {N}$, which are specified in Framework 3.1 above in terms of the Brownian motions $W^{n,m,j}:[0,T]\times \Omega \rightarrow \mathbb {R}^d$, $(n,m,j)\in \{1,2,\dots ,N\}\times \mathbb {N}\times \mathbb {N}$, via a function $H:[0,T]^2\times \mathbb {R}^d\times \mathbb {R}^d\rightarrow \mathbb {R}^d$ (cf. (150)). We refer the reader to (181) in Sect. 5.1 below, (183) in Sect. 5.2 below, (185) in Sect. 5.3 below, (206) in Sect. 5.4 below, and (211) in Sect. 5.5 below for concrete choices of H in the approximation of various example PDEs.

• (f) For every $n\in \{1,2,\dots ,N\}$, $m\in \mathbb {N}$ the optimization step in (154) in Framework 3.1 above is specified generically in terms of the functions $\psi ^n_m:\mathbb {R}^{\varrho }\rightarrow \mathbb {R}^{\mathfrak {d}}$ and $\Psi ^n_m:\mathbb {R}^{\varrho }\times \mathbb {R}^{\mathfrak {d}}\rightarrow \mathbb {R}^{\varrho }$ and the random variable $\Xi ^n_m:\Omega \rightarrow \mathbb {R}^{\varrho }$. This generic formulation covers a variety of SGD based optimization algorithms such as Adagrad [95], RMSprop, or Adam [96]. For example, in order to implement the Adam optimization algorithm, for every $n\in \{1,2,\dots ,N\}$, $m\in \mathbb {N}$ the random variable $\Xi ^n_m$ can be used to hold suitable first and second moment estimates (see (175) and (176) in Sect. 5 below for the concrete specification of these functions implementing the Adam optimization algorithm).

• (g) The processes $\mathbb {S}^n:\mathbb {N}_0\times \Omega \rightarrow \mathbb {R}^{\varsigma }$, $n\in \{1,2,\ldots ,N\}$, and functions $\mathcal {S}^n:\mathbb {R}^{\varsigma }\times \mathbb {R}^{\mathfrak {d}}\times (\mathbb {R}^d)^{\{0,1,\dots ,N\}\times \mathbb {N}}\rightarrow \mathbb {R}^\varsigma$, $n\in \{1,2,\dots ,N\}$, in Framework 3.1 above can be used to implement batch normalization; see [97] for details. Loosely speaking, for every $n\in \{1,2,\dots ,N\}$, $m\in \mathbb {N}$ the random variable $\mathbb {S}^n_m:\Omega \rightarrow \mathbb {R}^\varsigma$ then holds mean and variance estimates of the outputs of each layer of the approximating neural networks related to the minibatches that are used as inputs to the neural networks in computing the loss function at the corresponding gradient descent step.

4 Multilevel Picard approximation method for non-local PDEs

In this section we introduce in Framework 4.1 in Sect. 4.1 below our extension of the full history recursive multilevel Picard approximation method for approximating solutions of non-local nonlinear PDEs with Neumann boundary conditions. The MLP method was first introduced in E et al. [71] and Hutzenthaler et al. [69] and later extended in a number of directions; see E et al. [98] and Beck et al. [53] for recent surveys. We also refer the reader to Becker et al. [99] and E et al. [70] for numerical simulations illustrating the performance of MLP methods across a range of example PDE problems.

In Sect. 4.2 below, we will specify five concrete examples of (non-local) nonlinear PDEs and describe how Framework 4.1 can be specialized to compute approximate solutions to these example PDEs. These computations will be used in Sect. 5 to obtain reference values to compare the deep learning-based approximation method proposed in Sect. 3 above against.

4.1 Description of the proposed approximation method

Framework 4.1

(Multilevel Picard approximation method) Assume Framework 2.10, let $c,T\in (0,\infty )$, $\mathfrak {I}= \bigcup _{n\in \mathbb {N}} \mathbb {Z}^n$, $f \in C([0,T]\times D \times D \times \mathbb {R}\times \mathbb {R},\mathbb {R})$, $g\in C(D,\mathbb {R})$, $u \in C([0,T]\times D, \mathbb {R})$, assume $u\vert _{[0,T)\times D}\in C^{1,2}([0,T)\times D,\mathbb {R})$, let $\nu _x :\mathcal {B}( D)\rightarrow [0,1]$, $x \in D$, be probability measures, for every $x \in D$ let $Z^{\mathfrak {i}}_{ x } :\Omega \rightarrow D$, $\mathfrak {i}\in \mathfrak {I}$, be i.i.d. random variables, assume for every $A \in \mathcal {B}( D)$, $\mathfrak {i}\in \mathfrak {I}$ that $\mathbb {P}( Z_{ x }^{ \mathfrak {i}} \in A ) = \nu _x( A )$, for every $r_1\in [-\infty ,\infty )$, $r_2\in [r_1,\infty ]$ let $\phi _{r_1,r_2} :\mathbb {R}\rightarrow \mathbb {R}$ satisfy for every $y \in \mathbb {R}$ that

$$\begin{aligned} \phi _{r_1,r_2}(y) = \min \{r_2,\max \{r_1,y\}\}, \end{aligned}$$

(157)

let $(\Omega ,\mathcal {F}, \mathbb {P})$ be a probability space, let ${\mathcal {V}}^\mathfrak {i}:\Omega \rightarrow (0,1),$ $\mathfrak {i}\in \mathfrak {I}$, be independent $\mathcal {U}_{(0,1)}$-distributed random variables, let $V^\mathfrak {i}:[0,T]\times \Omega \rightarrow [0,T]$, $\mathfrak {i}\in \mathfrak {I}$, satisfy for every $t\in [0,T]$, $\mathfrak {i}\in \mathfrak {I}$ that

$$\begin{aligned} V^\mathfrak {i}_{t} = t+ (T-t){\mathcal {V}}^\mathfrak {i}, \end{aligned}$$

(158)

let $W^\mathfrak {i}:[0,T]\times \Omega \rightarrow \mathbb {R}^d$, $\mathfrak {i}\in \mathfrak {I}$, be independent standard Brownian motions, assume $({\mathcal {V}}^\mathfrak {i})_{\mathfrak {i}\in \mathfrak {I}}$ and $(W^\mathfrak {i})_{\mathfrak {i}\in \mathfrak {I}}$ are independent, let $\mu :\mathbb {R}^{d} \rightarrow \mathbb {R}^{d}$ and $\sigma :\mathbb {R}^{d}\rightarrow \mathbb {R}^{d\times d}$ be globally Lipschitz continuous, for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$ let $X^{x,\mathfrak {i}}_{t} = (X^{x,\mathfrak {i}}_{t,s})_{s\in [t,T]} :[t,T] \times \Omega \rightarrow \mathbb {R}^d$ be a stochastic process with continuous sample paths, let $(K_{n,l,m})_{n,l,m\in \mathbb {N}_0} \subseteq \mathbb {N}$, for every $\mathfrak {i}\in \mathfrak {I}$, $n,M \in \mathbb {N}_0$, $r_1\in [-\infty ,\infty )$, $r_2\in [r_1,\infty ]$ let $U^\mathfrak {i}_{n,M,r_1,r_2}:[0,T]\times \mathbb {R}^d\times \Omega \rightarrow \mathbb {R}^k$ satisfy for every $t\in [0,T]$, $x\in \mathbb {R}^d$ that

$$\begin{aligned} {\begin{matrix} &{} U^\mathfrak {i}_{n,M,r_1,r_2}(t,x) = \left[ \right. \textstyle \sum \limits _{l=0}^{n-1} \frac{(T-t)}{M^{n-l}} \textstyle \sum \limits _{m=1}^{M^{n-l}} \frac{1}{K_{n,l,m}} \textstyle \sum \limits _{k=1}^{K_{n,l,m}} \bigg [ f \Big ( V_t^{(\mathfrak {i},l,m)}, X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}}, Z^{(\mathfrak {i},l,m,k) }_{ X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}} },\\ &{}\quad \phi _{r_1,r_2}\Big ({U^{(\mathfrak {i},l,m)}_{l,M,r_1,r_2}\big ({V_t^{(\mathfrak {i},l,m)}, X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}}}\big )}\Big ), \phi _{r_1,r_2}\Big ({U^{(\mathfrak {i},l,m)}_{l,M,r_1,r_2}\big ({V_t^{(\mathfrak {i},l,m)}, Z^{(\mathfrak {i},l,m,k) }_{ X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}}}}\big )}\Big ) \Big )\\ &{}\quad - \mathbb {1}_\mathbb {N}(l) \, f \Big ( V_t^{(\mathfrak {i},l,m)}, X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}}, Z^{(\mathfrak {i},l,m,k)}_{ X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}} }, \phi _{r_1,r_2}\Big ({U^{(\mathfrak {i},l,-m)}_{\max \{l-1,0\},M,r_1,r_2}\big ({V_t^{(\mathfrak {i},l,m)}, X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}}}\big )}\Big ),\\ &{}\quad \phi _{r_1,r_2}\Big ({U^{(\mathfrak {i},l,-m)}_{\max \{l-1,0\},M,r_1,r_2} \big ({V_t^{(\mathfrak {i},l,m)},Z^{(\mathfrak {i},l,m,k) }_{ X^{x,(\mathfrak {i},l,m)}_{t,V_t^{(\mathfrak {i},l,m)}} }}\big )}\Big ) \Big )\bigg ]\left. \right] + \frac{\mathbb {1}_{\mathbb {N}}(n)}{M^n} \left[ {\textstyle \sum \limits _{m=1}^{M^n} g\big ({X^{x,(\mathfrak {i},0,-m)}_{t,T}}\big ) }\right] , \end{matrix}} \end{aligned}$$

(159)

assume for every $t \in [0,T)$, $x \in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$, and assume for every $t\in [0,T)$, $x \in D$ that $\Vert {u(t,x)} \Vert \le c(1+\Vert {x} \Vert ^{c})$, $u(T,x) = g(x)$, and

$$\begin{aligned}{} & {} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) +\tfrac{1}{2} {{\,\textrm{Trace}\,}}\big ({\sigma (x)[\sigma (x)]^{*}({{\,\textrm{Hess}\,}}_{x} u )(t,x)}\big ) + \langle {\mu (x), (\nabla _x u) (t,x)} \rangle \\{} & {} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\qquad + \int _D f (t,x,\textbf{x},u(t,x),u(t,\textbf{x})) \, \nu _x(\textrm{d}\textbf{x}) = 0 .\nonumber \end{aligned}$$

(160)

4.2 Examples for the approximation method

Example 4.2

(Fisher–KPP PDEs with Neumann boundary conditions) In this example we specialize Framework 4.1 to the case of certain Fisher–KPP PDEs with Neumann boundary conditions (cf., e.g., Bian et al. [36] and Wang et al. [40]).

Assume Framework 4.1, let $\epsilon \in (0,\infty )$, assume for every $t \in [0,T]$, $x,\textbf{x} \in D$, $y,\textbf{y} \in \mathbb {R}$, $v \in \mathbb {R}^d$ that $g(x)= \exp \big (- \tfrac{1}{4}\Vert {x} \Vert ^2\big )$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v = \epsilon v$, and $f(t,x,\textbf{x},y,\textbf{y})= y(1-y)$, and assume that for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$, $s\in [t,T]$ it holds $\mathbb {P}$-a.s. that

$$\begin{aligned} X^{x,\mathfrak {i}}_{t,s} = R\Bigg (x,x + \int _{t}^{s} \mu \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}r + \int ^{s}_{t} \sigma \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}W^{\mathfrak {i}}_{r} \Bigg ) = R(x,x+\epsilon (W^\mathfrak {i}_s-W^\mathfrak {i}_t)) . \end{aligned}$$

(161)

The solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (160) then satisfies that for every $t\in [0,T)$, $x\in \partial _D$ it holds that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and that for every $t\in [0,T)$, $x\in D$ it holds that $u(T,x) = \exp (- \tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) + \tfrac{\epsilon ^2}{2}(\Delta _x u) (t,x) + u(t,x)\big ({1 - u(t,x) }\big ) = 0 . \end{aligned}$$

(162)

Example 4.3

(Non-local competition PDEs) In this example we specialize Framework 4.1 to the case of certain non-local competition PDEs (cf., e.g., Doebeli and Ispolatov [47], Berestycki et al. [38], Perthame and Génieys [37], and Génieys et al. [42]).

Assume Framework 4.1, let $\mathfrak s,\epsilon \in (0,\infty )$, assume for every $x \in \mathbb {R}^d$, $A \in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A) = \pi ^{-\nicefrac {d}{2}}\mathfrak {s}^{-d}\int _A \exp \bigl (-\mathfrak {s}^{-2}\Vert {x - \textbf{x}} \Vert ^2\bigr )\,\textrm{d}\textbf{x}$, assume for every $t \in [0,T]$, $v,x,\textbf{x} \in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$ that $g(x)= \exp (- \tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v = \epsilon v$, and $f(t,x,\textbf{x},y,\textbf{y})= y(1 -\textbf{y}\pi ^{\nicefrac {d}{2}}\mathfrak {s}^d)$, and assume that for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$, $s\in [t,T]$ it holds $\mathbb {P}$-a.s. that

$$\begin{aligned} X^{x,\mathfrak {i}}_{t,s} = x + \int _{t}^{s} \mu \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}r + \int ^{s}_{t} \sigma \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}W^{\mathfrak {i}}_{r} = x+\epsilon (W^\mathfrak {i}_s-W^\mathfrak {i}_t) . \end{aligned}$$

(163)

The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (160) then satisfies that for every $t\in [0,T)$, $x\in \mathbb {R}^d$ it holds that $u(T,x) = \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) + \tfrac{\epsilon ^2}{2}(\Delta _x u) (t,x) + u(t,x)\left( 1 - \int _{\mathbb {R}^d} u(t,\textbf{x})\,\exp \big ({-\tfrac{\Vert {x-\textbf{x}} \Vert ^2}{\mathfrak {s}^2}}\big ) \, \textrm{d}\textbf{x} \right) = 0 . \end{aligned}$$

(164)

Example 4.4

(Non-local sine-Gordon PDEs) In this example we specialize Framework 4.1 to the case of certain non-local sine-Gordon type PDEs (cf., e.g., Hairer and Shen [9], Barone et al. [6], and Coleman [8]).

Assume Framework 4.1, let $\mathfrak s,\epsilon \in (0,\infty )$ , assume for every $x \in \mathbb {R}^d$, $A \in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A) = \pi ^{-\nicefrac {d}{2}}\mathfrak {s}^{-d}\int _A \exp \left( -\mathfrak {s}^{-2}\Vert {x - \textbf{x}} \Vert ^2\right) \,\textrm{d}\textbf{x}$, assume for every $t \in [0,T]$, $v,x,\textbf{x} \in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$ that $g(x)= \exp (- \tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v = \epsilon v$, and $f(t,x,\textbf{x},y,\textbf{y})= \sin (y) -\textbf{y}\pi ^{\nicefrac {d}{2}}\mathfrak {s}^d$, and assume that for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$, $s\in [t,T]$ it holds $\mathbb {P}$-a.s. that

$$\begin{aligned} X^{x,\mathfrak {i}}_{t,s} = x + \int _{t}^{s} \mu \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}r + \int ^{s}_{t} \sigma \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}W^{\mathfrak {i}}_{r} = x+\epsilon (W^\mathfrak {i}_s-W^\mathfrak {i}_t) . \end{aligned}$$

(165)

The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (160) then satisfies that for every $t\in [0,T)$, $x\in \mathbb {R}^d$ it holds that $u(T,x) = \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) + \tfrac{\epsilon ^2}{2}(\Delta _x u)(t,x) + \sin ( u(t,x) ) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, \exp \big ({-\tfrac{\Vert {x-\textbf{x}} \Vert ^2}{\mathfrak {s}^2}}\big )\,\textrm{d}\textbf{x} = 0 . \end{aligned}$$

(166)

Example 4.5

(Replicator-mutator PDEs) In this example we specialize Framework 4.1 to the case of certain d-dimensional replicator-mutator PDEs (cf., e.g., Hamel et al. [26]).

Assume Framework 4.1, let $\mathfrak {m}_1, \mathfrak {m}_2, \dots ,\mathfrak {m}_d, \mathfrak {s}_1, \mathfrak {s}_2, \dots , \mathfrak {s}_d,\mathfrak {u}_1, \mathfrak {u}_2,\dots ,\mathfrak {u}_d \in \mathbb {R}$ , let $a :\mathbb {R}^d \rightarrow \mathbb {R}$ satisfy for every $x \in \mathbb {R}^d$ that $a(x) = -\frac{1}{2}\Vert {x} \Vert ^2$, assume for every $x \in \mathbb {R}^d$, $A \in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A) = \int _{A\cap [-\nicefrac 12,\nicefrac 12]^d} \textrm{d}{\textbf{x}}$, assume for every $t \in [0,T]$, $v= (v_1,\dots ,v_d),\,x = (x_1,\dots ,x_d)\in \mathbb {R}^d$, $\textbf{x} \in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$ that $g(x)= (2\pi )^{-\nicefrac {d}{2}} \big [{\prod _{ i = 1 }^d |{\mathfrak {s}_i} |^{-\nicefrac {1}{2}}}\big ] \exp \big ({-\sum _{i = 1}^d \, \frac{(x_i - \mathfrak {u}_i )^2}{2\mathfrak {s}_i}}\big )$, $\mu (x)=(0,\dots ,0)$, $\sigma (x)v=(\mathfrak {m}_1 v_1, \dots , \mathfrak {m}_d v_d)$, and

$$\begin{aligned} f(t,x,\textbf{x},y,\textbf{y}) = y \big (a(x) - \textbf{y} a({\textbf{x}}) \big ) , \end{aligned}$$

(167)

and assume that for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$, $s\in [t,T]$ it holds $\mathbb {P}$-a.s. that

$$\begin{aligned} X^{x,\mathfrak {i}}_{t,s} = x + \int _{t}^{s} \mu \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}r + \int ^{s}_{t} \sigma \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}W^{\mathfrak {i}}_{r} = x+\sigma (0)(W^\mathfrak {i}_s-W^\mathfrak {i}_t) . \end{aligned}$$

(168)

The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (160) then satisfies that for every $t\in [0,T)$, $x = (x_1,\dots ,x_d) \in \mathbb {R}^d$ it holds that $u(T,x)= (2\pi )^{-\nicefrac {d}{2}}\big [{ \prod _{ i = 1 }^d |{\mathfrak {s}_i} |^{-\nicefrac {1}{2}}}\big ] \exp \big ({-\sum _{i = 1}^d \, \frac{(x_i - \mathfrak {u}_i )^2}{2\mathfrak {s}_i}}\big )$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) + u(t,x)\Bigg (a(x) - \int _{[-\nicefrac 12,\nicefrac 12]^d} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} \Bigg ) + \sum _{i=1}^{d} \tfrac{1}{2} |{\mathfrak {m}_i} |^2 \big ({\tfrac{\partial ^2 }{\partial x_i^2} u}\big ) (t,x) = 0 . \end{aligned}$$

(169)

Example 4.6

(Allen–Cahn PDEs with conservation of mass) In this example we specialize Framework 4.1 to the case of certain Allen–Cahn PDEs with cubic nonlinearity, conservation of mass, and no-flux boundary conditions (cf., e.g., Rubinstein and Sternberg [10]).

Assume Framework 4.1, let $\epsilon \in (0,\infty )$ , assume for every $x \in D$, $A \in \mathcal {B}(D)$ that $\nu _x(A) = \int _A \textrm{d}\textbf{x}$, assume for every $t \in [0,T]$, $x,\textbf{x} \in D$, $y,\textbf{y} \in \mathbb {R}$, $v \in \mathbb {R}^d$ that $g(x)= \exp (- \tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v = \epsilon v$, and $f(t,x,{\textbf{x}},y,{\textbf{y}})= y - y^3 - (\textbf{y} - {\textbf{y}}^3)$, and assume that for every $x\in \mathbb {R}^{d}$, $\mathfrak {i}\in \mathfrak {I}$, $t\in [0,T]$, $s\in [t,T]$ it holds $\mathbb {P}$-a.s. that

$$\begin{aligned} X^{x,\mathfrak {i}}_{t,s} = R\Bigg (x,x + \int _{t}^{s} \mu \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}r + \int ^{s}_{t} \sigma \big ({X^{x,\mathfrak {i}}_{t,r}}\big ) \, \textrm{d}W^{\mathfrak {i}}_{r} \Bigg ) = R(x,x+\epsilon (W^\mathfrak {i}_s-W^\mathfrak {i}_t)) . \end{aligned}$$

(170)

The solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (160) then satisfies that for every $t\in [0,T)$, $x\in \partial _D$ it holds that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and that for every $t\in [0,T)$, $x\in D$ it holds that $u(T,x) = \exp (- \tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) + \tfrac{\epsilon ^2}{2} (\Delta _x u)(t,x) + u(t,x) - [u(t,x)]^3 - \int _{[-\nicefrac {1}{2},\nicefrac {1}{2}]^d} u(t,\textbf{x}) - [u(t,\textbf{x})]^3\, \textrm{d}\textbf{x} = 0 . \end{aligned}$$

(171)

5 Numerical simulations

In this section we illustrate the performance of the machine learning-based approximation method proposed in Framework 3.1 in Sect. 3.2 above by means of numerical simulations for five concrete (non-local) nonlinear PDEs; see Sects. 5.1, 5.2, 5.3, 5.4, and 5.5 below. In each of these numerical simulations we employ the general machine learning-based approximation method proposed in Framework 3.1 with certain 4-layer neural networks in conjunction with the Adam optimizer (cf. (175) and (176) in Framework 5.1 below and Kingma and Ba [96]).

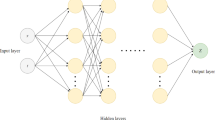
More precisely, in each of the numerical simulations in Sects. 5.1, 5.2, 5.3, 5.4, and 5.5 the functions ${\mathbb {V}}^{j,\textbf{s}}_n:\mathbb {R}^{\mathfrak d}\times \mathbb {R}^d\rightarrow \mathbb {R}$ with $n \in \{ 1, 2, \dots , N\}$, $j \in \{ 1, 2, \dots , 8000 \}$, $\textbf{s} \in \mathbb {R}^{\varsigma }$ are implemented as N fully-connected feedforward neural networks. These neural networks consist of 4 layers (corresponding to 3 affine linear transformations in the neural networks) where the input layer is d-dimensional (with d neurons on the input layer), where the two hidden layers are both $(d+50)$-dimensional (with $d+50$ neurons on each of the two hidden layers), and where the output layer is 1-dimensional (with 1 neuron on the output layer). We refer to Fig. 2 for a graphical illustration of the neural network architecture used in the numerical simulations in Sects. 5.1, 5.2, 5.3, 5.4, and 5.5.

Fig. 2

Graphical illustration of the neural network architecture used in the numerical simulations. In Sects. 5.1, 5.2, 5.3, 5.4, and 5.5 we employ neural networks with 4 layers (corresponding to 3 affine linear transformations in the neural networks) with d neurons on the input layer (corresponding to a d-dimensional input layer), with $d + 50$ neurons on the 1st hidden layer (corresponding to a $(d+50)$-dimensional 1st hidden layer), with $d + 50$ neurons on the 2nd hidden layer (corresponding to a $(d+50)$-dimensional 2nd hidden layer), and with 1 neuron on the output layer (corresponding to a 1-dimensional output layer) in the numerical simulations

As activation functions just in front of the two hidden layers we employ, in Sects. 5.1, 5.2, 5.3, and 5.4 below, multidimensional versions of the hyperbolic tangent function

$$\begin{aligned} \mathbb {R}\ni x \mapsto (e^x + e^{-x})^{-1} (e^{x} - e^{-x}) \in \mathbb {R}, \end{aligned}$$

(172)

and we employ, in Sect. 5.5 below, multidimensional versions of the ReLU function

$$\begin{aligned} \mathbb {R}\ni x\mapsto \max \{x,0\}\in \mathbb {R}. \end{aligned}$$

(173)

In addition, in Sects. 5.1, 5.2, and 5.4 we use the square function and $\mathbb {R}\ni x \mapsto x^2 \in \mathbb {R}$ as activation function just in front of the output layer and in Sects. 5.3 and 5.5 we use the identity function $\mathbb {R}\ni x \mapsto x \in \mathbb {R}$ as activation function just in front of the output layer. Furthermore, we employ Xavier initialization to initialize all neural network parameters; see Glorot and Bengio [100] for details. We did not employ batch normalization in our simulations.

Each of the numerical experiments presented below was performed with the Julia library HighDimPDE.jl on a NVIDIA TITAN RTX GPU with 1350 MHz core clock and 24 GB GDDR6 memory with 7000 MHz clock rate where the underlying system consisted of an AMD EPYC 7742 64-core CPU with 2TB memory running Julia 1.7.2 on Ubuntu 20.04.3.

The algorithms proposed in Framework 3.1 and Sect. 4.1 have been implemented as a Julia library named HighDimPDE, which belongs to the SciML software ecosystem. The library is listed in the official registry of general Julia packages, and its source code can be accessed at https://github.com/SciML/HighDimPDE.jl. The exact source code we used for the simulations in this section is available from two sources: It is included (along with the source code of the library) in the arXiv version of this article available at https://arxiv.org/abs/2205.03672 where the source files can be downloaded by choosing “Other sources” under “Download” and then following the link “Download sources” (or using the URL https://arxiv.org/e-print/2205.03672). Additionally, the specific Julia source code used for the simulations in this section can be found in a dedicated Github repository located at https://github.com/vboussange/HighDimPDE_examples.

Framework 5.1

Assume Framework 3.1, assume $\mathfrak {d}=(d+50)(d+1)+ (d+50)(d+51)+(d+51)$, let $\varepsilon ,\beta _1,\beta _2\in \mathbb {R}$, $(\gamma _m)_{m\in \mathbb {N}}\subseteq (0,\infty )$ satisfy $\varepsilon =10^{-8}$, $\beta _1 = \tfrac{9}{10}$, and $\beta _2 = \tfrac{999}{1000}$, let $g:D \rightarrow \mathbb {R}$, $\mu :D\rightarrow \mathbb {R}^d$, and $\sigma :D\rightarrow \mathbb {R}^{d\times d}$ be continuous, let $u=(u(t,x))_{(t,x) \in [0,T]\times D} \in C^{1,2}([0,T]\times D,\mathbb {R})$ have at most polynomially growing partial derivatives, assume for every $t\in (0,T]$, $x\in \partial _D$ that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$, assume for every $t\in [0,T]$, $x\in D$, $j \in \mathbb {N}$, $\textbf{s} \in \mathbb {R}^\varsigma$ that $u(0,x)=g(x) = \mathbb V^{ j, \textbf{s} }_0( \theta , x )$, $\int _D\big |{f\big ({t,x,\textbf{x}, u(t,x),u(t,\textbf{x}) }\big ) }\big | \, \nu _x(\textrm{d}\textbf{x}) < \infty$, and

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x)&= \tfrac{ 1 }{ 2 } {{\,\textrm{Trace}\,}}\big ({\sigma (x) [ \sigma (x) ]^*( {{\,\textrm{Hess}\,}}_x u)( t,x )}\big ) + \big \langle { \mu (x), ( \nabla _x u )( t,x ) }\big \rangle \\&\quad + \int _{D} f\big ({t,x,\textbf{x}, u(t,x),u(t,\textbf{x}) }\big ) \, \nu _x(\textrm{d}\textbf{x}) , \end{aligned} \end{aligned}$$

(174)

assume for every $m\in \mathbb {N}$, $i\in \{0,1,\ldots ,N\}$ that $J_m = 8000$, $t_i = \tfrac{iT}{N}$, and $\varrho = 2 \mathfrak {d}$, and assume for every $n \in \{1,2,\dots ,N\}$, $m\in \mathbb {N}$, $x=(x_1, \ldots , x_{\mathfrak {d}})$, $y=(y_1, \ldots , y_{\mathfrak {d}})$, $\eta = ( \eta _1, \ldots , \eta _{\mathfrak {d}} )\in \mathbb {R}^{\mathfrak {d}}$ that

$$\begin{aligned} \Xi ^n_0(x,y,\eta ) = 0,\quad \Psi ^n_m ( x , y , \eta ) = \big ({\beta _1 x + (1-\beta _1) \eta , \beta _2 y + (1-\beta _2) ((\eta _1)^2,\ldots ,(\eta _{\mathfrak {d}})^2)}\big ),\nonumber \\ \end{aligned}$$

(175)

and

$$\begin{aligned} \psi ^n_m ( x,y ) = \bigg ({ \Big [{ \sqrt{\tfrac{|{y_1} |}{1-(\beta _2)^m}} + \varepsilon }\Big ]^{-1} \frac{\gamma _m x_{1}}{1-(\beta _1)^m}, \ldots , \Big [{ \sqrt{\tfrac{|{y_{\mathfrak {d}}} |}{1-(\beta _2)^m}} + \varepsilon }\Big ]^{-1} \frac{\gamma _m x_{\mathfrak {d}}}{1-(\beta _1)^m} }\bigg ) . \end{aligned}$$

(176)

In Sects. 5.1, 5.2, 5.3, 5.4, and 5.5 below, we use the machine learning-based approximation method in Framework 5.1 to approximately calculate the solutions to a variety of PDEs with a non-local term and/or Neumann boundary conditions in dimension $d\in \{1,2,5,10\}$ and with time horizon $T\in \{\nicefrac 15,\nicefrac 12,1\}$. We evaluate these approximations by comparing them to a reference solution. Specifically, in Sects. 5.1, 5.2, 5.3, and 5.5 we use the multilevel Picard approximation method presented in Framework 4.1 to compute an approximation for $u(T,(0,\dots ,0))$ which we use as the reference solution to approximate the unknown exact solution $u(T,(0,\dots ,0))$. For the PDEs treated in Sect. 5.4 we can compute the exact solution directly and use this exact solution as the reference solution. In all cases, we run the simulation 5 times, for each value of d and for each value of T, thus obtaining 5 independent realizations of the random variable ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We use these to approximately compute and report, in Tables 1, 2, 3, 4, and 7 below, the mean

$$\begin{aligned} \mathbb E\big [{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))\big ], \end{aligned}$$

(177)

the standard deviation

$$\begin{aligned} \Bigl ( \mathbb {E}\big [|{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0)) - \mathbb {E}[{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))]} |^2\big ] \Bigr )^{\!\nicefrac 12}, \end{aligned}$$

(178)

the relative $L^1$-approximation error

$$\begin{aligned} \mathbb {E}\Biggl [\tfrac{|{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0)) - u(T,(0,\dots ,0))} |}{|{u(T,(0,\dots ,0))} |}\Biggr ], \end{aligned}$$

(179)

the standard deviation

$$\begin{aligned} \biggl (\mathbb {E}\biggl [\Bigg |{\tfrac{|{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0)) - u(T,(0,\dots ,0))} |}{|{u(T,(0,\dots ,0))} |} - \mathbb {E}\Biggl [\tfrac{|{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0)) - u(T,(0,\dots ,0))} |}{|{u(T,(0,\dots ,0))} |}\Biggr ]}\Bigg |^2\biggr ] \biggr )^{\!\!\nicefrac 12} \end{aligned}$$

(180)

of the relative $L^1$-approximation error, as well as the average of the runtimes of the 5 independent runs. This runtime is measured from the start of the training of the first neural network until the end of the training of the final neural network (note that the time required for the evaluation of the neural networks is negligible).

5.1 Fisher–KPP PDEs with Neumann boundary conditions

In this subsection we use the machine learning-based approximation method in Framework 5.1 to approximately calculate the solutions of certain Fisher–KPP PDEs with Neumann boundary conditions (cf., e.g., Bian et al. [36] and Wang et al. [40]).

Assume Framework 5.1, let $\epsilon \in (0,\infty )$ satisfy $\epsilon = \tfrac{1}{10}$, assume $d\in \{1,2,5,10\}$, $D = [-\nicefrac {1}{2},\nicefrac {1}{2}]^d$, $T\in \{\nicefrac {1}{5},\nicefrac {1}{2},1\}$, $N=10$, $K_1 = K_2 = \ldots = K_N= 1$, and $M_1 = M_2 = \ldots = M_N = 500$, assume for every $n,m,j\in \mathbb {N}$, $\omega \in \Omega$ that $\xi ^{n,m,j}(\omega )=(0,\dots ,0)$, assume for every $m \in \mathbb {N}$ that $\gamma _m = 10^{-2}$, and assume for every $s,t \in [0,T]$, $x,\textbf{x} \in D$, $y,\textbf{y} \in \mathbb {R}$, $v \in \mathbb {R}^d$ that $g(x)= \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v =\epsilon v$, $f(t,x,\textbf{x},y,\textbf{y} )= y(1-y)$, and

$$\begin{aligned} H(t,s,x,v) = R(x,x+\mu (x)(t-s)+\sigma (x)v) = R(x,x+\epsilon v) \end{aligned}$$

(181)

(cf. (139) and (150)). The solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (174) then satisfies that for every $t\in (0,T]$, $x\in \partial _D$ it holds that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and that for every $t\in [0,T]$, $x\in D$ it holds that $u(0,x) = \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) = \tfrac{\epsilon ^2}{2}(\Delta _x u) (t,x) + u(t,x)\big ({1 - u(t,x) }\big ) . \end{aligned}$$

(182)

In (182) the function $u:[0,T]\times D\rightarrow \mathbb {R}$ models the proportion of a particular type of alleles in a biological population spatially structured over D. For every $t\in [0,T]$, $x\in \mathbb {R}^d$ the number $u(t,x) \in \mathbb {R}$ describes the proportion of individuals with a particular type of alleles located at position $x = (x_1, \dots , x_d) \in \mathbb {R}^d$ at time $t \in [0,T]$.

For each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 15,\nicefrac 12,1\}$ we approximate the unknown value $u(T,(0,\dots ,0))$ by computing 5 independent realizations of ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We report in Table 1 approximations of the mean and the standard deviation of this random variable as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error (see the discussion below Framework 5.1 for more details). For the latter two statistics, the reference value which is used as an approximation for the unknown value $u(T,(0,\ldots ,0))$ of the exact solution of the PDE in (182) is computed via the MLP approximation method for non-local nonlinear PDEs in Framework 4.1 as described in Example 4.2 (cf. Beck et al. [101, Remark 3.3]). More precisely, we apply Example 4.2 with $d\in \{1,2,5,10\}$, $T\in \{\nicefrac 15, \nicefrac 12, 1\}$, $D=[-\nicefrac 12,\nicefrac 12]^d$, $\epsilon =\frac{1}{10}$ in the notation of Example 4.2 and we use the mean of 5 independent realizations of $U^{(0)}_{5,5,0,\infty }(0,(0,\dots ,0))$ as the reference value.

Table 1 Numerical simulations for the approximation method in Framework 3.1 in the case of the Fisher–KPP PDEs with Neumann boundary conditions in (182) in Sect. 5.1

5.2 Non-local competition PDEs

In this subsection we use the machine learning-based approximation method in Framework 5.1 to approximately calculate the solutions of certain non-local competition PDEs (cf., e.g., Doebeli and Ispolatov [47], Berestycki et al. [38], Perthame and Génieys [37], and Génieys et al. [42]).

Assume Framework 5.1, let $\mathfrak s,\epsilon \in (0,\infty )$ satisfy $\mathfrak {s} = \epsilon =\tfrac{1}{10}$, assume $d\in \{1,2,5,10\}$, $D= \mathbb {R}^d$, $T\in \{\nicefrac {1}{5},\nicefrac {1}{2},1\}$, $N=10$, $K_1 = K_2 = \cdots = K_N= 1$, and $M_1 = M_2 = \cdots = M_N = 500$, assume for every $n,m,j\in \mathbb {N}$, $\omega \in \Omega$ that $\xi ^{n,m,j}(\omega )=(0,\dots ,0)$, assume for every $m \in \mathbb {N}$ that $\gamma _m = 10^{-2}$, and assume for every $s,t \in [0,T]$, $v,x,\textbf{x}\in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$, $A \in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A) = \pi ^{-\nicefrac {d}{2}}\mathfrak {s}^{-d}\int _A \exp \big (-\mathfrak {s}^{-2}\Vert {x - \textbf{x}} \Vert ^2\big )\,\textrm{d}\textbf{x}$, $g(x)= \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v=\epsilon v$, $f(t,x,\textbf{x},y,\textbf{y})= y(1 - \textbf{y} \mathfrak {s}^d\pi ^{\nicefrac {d}{2}})$, and

$$\begin{aligned} H(t,s,x,v) = x + \mu (x)(t-s)+ \sigma (x)v = x+\epsilon v \end{aligned}$$

(183)

(cf. (139) and (150)). The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (174) then satisfies that for every $t\in [0,T]$, $x\in \mathbb {R}^d$ it holds that $u(0,x)=\exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) = \tfrac{\epsilon ^2}{2}(\Delta _x u)(t,x) + u(t,x) \Bigg (1 - \int _{\mathbb {R}^d} u(t,\textbf{x}) \exp \big ({-\tfrac{\Vert {x-\textbf{x}} \Vert ^2}{\mathfrak {s}^2} }\big ) \, \textrm{d}\textbf{x} \Bigg ) . \end{aligned}$$

(184)

In (184) the function $u:[0,T]\times \mathbb {R}^d\rightarrow \mathbb {R}$ models the evolution of a population characterized by a set of d biological traits under the combined effects of selection, competition, and mutation. For every $t\in [0,T]$, $x\in \mathbb {R}^d$ the number $u(t,x) \in \mathbb {R}$ describes the number of individuals with traits $x = (x_1, \dots , x_d) \in \mathbb {R}^d$ at time $t \in [0,T]$.

For each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 15,\nicefrac 12,1\}$ we approximate the unknown value $u(T,(0,\dots ,0))$ by computing 5 independent realizations of ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We report in Table 2 approximations of the mean and the standard deviation of this random variable as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error (see the discussion below Framework 5.1 for more details). For the latter two statistics, the reference value which is used as an approximation for the unknown value $u(T,(0,\ldots ,0))$ of the exact solution of the PDE in (184) is computed via the MLP approximation method for non-local nonlinear PDEs in Framework 4.1 as described in Example 4.3 (cf. Beck et al. [101, Remark 3.3]). More precisely, we apply Example 4.3 with $d\in \{1,2,5,10\}$, $T\in \{\nicefrac 15, \nicefrac 12, 1\}$, $D=\mathbb {R}^d$, $\mathfrak s=\epsilon =\frac{1}{10}$ in the notation of Example 4.3 and we use the mean of 5 independent realizations of $U^{(0)}_{5,5,0,\infty }(0,(0,\dots ,0))$ as the reference value.

Table 2 Numerical simulations for the approximation method in Framework 3.1 in the case of the non-local competition PDEs in (184) in Sect. 5.2

5.3 Non-local sine-Gordon type PDEs

In this subsection we use the machine learning-based approximation method in Framework 5.1 to approximately calculate the solutions of non-local sine-Gordon type PDEs (cf., e.g., Hairer and Shen [9], Barone et al. [6], and Coleman [8]).

Assume Framework 5.1, let $\mathfrak s,\epsilon \in (0,\infty )$ satisfy $\mathfrak {s} = \epsilon =\tfrac{1}{10}$, assume $d\in \{1,2,5,10\}$, $D= \mathbb {R}^d$, $T\in \{\nicefrac {1}{5},\nicefrac {1}{2},1\}$, $N=10$, $K_1 = K_2 = \cdots = K_N= 1$, and $M_1 = M_2 = \cdots = M_N = 500$, assume for every $n,m,j\in \mathbb {N}$, $\omega \in \Omega$ that $\xi ^{n,m,j}(\omega )=(0,\dots ,0)$, assume for every $m \in \mathbb {N}$ that $\gamma _m = 10^{-3}$, and assume for every $s,t \in [0,T]$, $v,x,\textbf{x} \in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$, $A \in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A) = \pi ^{-\nicefrac {d}{2}}\mathfrak {s}^{-d}\int _A \exp \big (-\mathfrak {s}^{-2}\Vert {x - \textbf{x}} \Vert ^2\big )\,\textrm{d}\textbf{x}$, $g(x)= \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0,\dots ,0)$, $\sigma (x) v = \epsilon v$, $f(t,x,\textbf{x},y,\textbf{y})= \sin (y) - \textbf{y} \pi ^{\nicefrac {d}{2}}\mathfrak {s}^d$, and

$$\begin{aligned} H(t,s,x,v) = x + \mu (x)(t-s)+ \sigma (x)v = x+\epsilon v \end{aligned}$$

(185)

(cf. (139) and (150)). The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (174) then satisfies that for every $t\in [0,T]$, $x\in \mathbb {R}^d$ it holds that $u(0,x)=\exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) = \tfrac{\epsilon ^2}{2}(\Delta _x u)(t,x) + \sin ( u(t,x) ) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, \exp \big ({-\tfrac{\Vert {x-\textbf{x}} \Vert ^2}{\mathfrak {s}^2}}\big )\,\textrm{d}\textbf{x} . \end{aligned}$$

(186)

For each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 15,\nicefrac 12,1\}$ we approximate the unknown value $u(T,(0,\dots ,0))$ by computing 5 independent realizations of ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We report in Table 3 approximations of the mean and the standard deviation of this random variable as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error (see the discussion below Framework 5.1 for more details). For the latter two statistics, the reference value which is used as an approximation for the unknown value $u(T,(0,\ldots ,0))$ of the exact solution of the PDE in (186) is computed via the MLP approximation method for non-local nonlinear PDEs in Framework 4.1 as described in Example 4.4 (cf. Beck et al. [101, Remark 3.3]). More precisely, we apply Example 4.4 with $d\in \{1,2,5,10\}$, $T\in \{\nicefrac 15, \nicefrac 12, 1\}$, $D=\mathbb {R}^d$, $\mathfrak s=\epsilon =\frac{1}{10}$ in the notation of Example 4.4 and we use the mean of 5 independent realizations of $U^{(0)}_{5,5,-\infty ,\infty }(0,(0,\dots ,0))$ as the reference value.

Table 3 Numerical simulations for the approximation method in Framework 3.1 in the case of the non-local sine-Gordon PDEs in (186) in Sect. 5.3

5.4 Replicator-mutator PDEs

In this subsection we use both the machine learning-based approximation method in Framework 5.1 and the MLP approximation method in Framework 4.1 to approximately calculate the solutions of certain replicator-mutator PDEs describing the dynamics of a phenotype distribution under the combined effects of selection and mutation (cf., e.g., Hamel et al. [26]). The solutions to the PDEs we are trying to approximate in this subsection can be represented explicitly (cf., e.g., Lemma 5.2 below). The gives us the opportunity to compare the performance of the two approximation methods presented here and it also allows us to evaluate the capability of the machine learning-based approximation method in Framework 5.1 to produce approximations on an entire subset of the domain.

Exact solutions. The following results, Lemma 5.2 below, give an explicit representation of the exact solutions of certain replicator-mutator PDEs. In (190) the function $u:[0,T]\times \mathbb {R}^d\rightarrow \mathbb {R}$ models the evolution of the phenotype distribution of a population composed of a set of d biological traits under the combined effects of selection and mutation. For every $t\in [0,T]$, $x\in \mathbb {R}^d$ the number $u(t,x) \in \mathbb {R}$ describes the number of individuals with traits $x = (x_1, \dots , x_d) \in \mathbb {R}^d$ at time $t \in [0,T]$. The function a models a quadratic fitness function.

Lemma 5.2

Let $d \in \mathbb {N}$, $\mathfrak {u}_1,\mathfrak {u}_2, \dots ,\mathfrak {u}_d\in \mathbb {R}$, $\mathfrak {m}_1,\mathfrak {m}_2, \dots ,\mathfrak {m}_d, \mathfrak {s}_1,\mathfrak {s}_2, \dots ,\mathfrak {s}_d \in (0,\infty )$, let $a :\mathbb {R}^d \rightarrow \mathbb {R}$ satisfy for every $x \in \mathbb {R}^d$ that $a(x) = -\frac{1}{2} \Vert {x} \Vert ^2$, for every $i \in \{1,2,\dots ,d\}$ let $\mathfrak {S}_i :[0,\infty ) \rightarrow (0,\infty )$ and $\mathfrak {U}_i :[0,\infty ) \rightarrow \mathbb {R}$ satisfy for every $t \in [0,\infty )$ that

$$\begin{aligned}{} & {} \mathfrak {S}_i(t) = \mathfrak {m}_i \left[ { \frac{\mathfrak {m}_i \sinh (\mathfrak {m}_i t) + \mathfrak {s}_i \cosh (\mathfrak {m}_i t)}{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)}}\right] \nonumber \\{} & {} \quad \text {and} \quad \mathfrak {U}_i(t) = \frac{\mathfrak {m}_i \mathfrak {u}_i}{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)} , \end{aligned}$$

(187)

and let $u :[0,\infty ) \times \mathbb {R}^d \rightarrow \mathbb {R}$ satisfy for every $t \in [0,\infty )$, $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ that

$$\begin{aligned} u(t,x) = (2\pi )^{- \nicefrac {d}{2}} {\left[ \prod _{ i = 1 }^d |{\mathfrak {S}_i(t)} |^{- \nicefrac {1}{2}}\right] } \exp \bigg (-\sum _{i = 1}^d \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}\bigg ) . \end{aligned}$$

(188)

Then

• (i) it holds that $u \in C^{1,2}([0,\infty )\times \mathbb {R}^d,\mathbb {R})$,

• (ii) it holds for every $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ that

  $$\begin{aligned} u(0,x) = (2\pi )^{-\nicefrac {d}{2}} \left[ {\prod _{ i = 1 }^d |{\mathfrak {s}_i} |^{-\nicefrac {1}{2}}}\right] \exp \bigg (-\sum _{i = 1}^d \frac{(x_i - \mathfrak {u}_i )^2}{2\mathfrak {s}_i}\bigg ),\nonumber \\ \end{aligned}$$

  (189)

  and

• (iii) it holds for every $t \in [0,\infty )$, $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ that

  $$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) = u(t,x)\Bigg (a(x) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x}\Bigg ) + \sum _{i=1}^{d} \tfrac{1}{2} |{\mathfrak {m}_i} |^2\big ({\tfrac{\partial ^2 }{\partial x_i^2} u}\big ) (t,x) . \end{aligned}$$

  (190)

Proof of Lemma 5.2

First, note that the fact that for every $i \in \{1,2,\dots ,d\}$ it holds that $\mathfrak {S}_i \in C^{\infty }([0,\infty ),(0,\infty ))$, the fact that for every $i \in \{1,2,\dots ,d\}$ it holds that $\mathfrak {U}_i \in C^{\infty }([0,\infty ),\mathbb {R})$, and (188) establish item (i). Moreover, observe that the fact that for every $i \in \{1,2,\dots ,d\}$ it holds that $\mathfrak {S}_i(0) = \mathfrak {s}_i$, the fact that for every $i \in \{1,2,\dots ,d\}$ it holds that $\mathfrak {U}_i(0) = \mathfrak {u}_i$, and (187) prove item (ii). Next note that (188) ensures that for every $t \in [0,\infty )$, $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} u(t,x) = \prod _{i=1}^d \Bigg [ (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \Bigg ( - \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}\Bigg ) \Bigg ] . \end{aligned}$$

(191)

The product rule hence implies that for every $t \in [0,\infty )$, $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&\big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) \\&=\frac{\partial }{\partial t} \left( \prod _{i=1}^d \Bigg [ (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \Bigg ( - \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)} \Bigg )\Bigg ] \right) \\&= \sum _{i=1}^d \left[ \left[ \prod \nolimits _{ j \in \{ 1,\dots ,d \} \backslash \{i\}} \left( (2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \left( -\frac{(x_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)}\right) \right) \right] \right. \\&\quad \left. \cdot \left[ \frac{\partial }{\partial t} \left( (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( - \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}\right) \right) \right] \right] . \end{aligned} \end{aligned}$$

(192)

The chain rule, the product rule, and (191) therefore show that for every $t \in [0,\infty )$, $x = (x_1,\dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned}{} & {} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) \nonumber \\{} & {} \quad = \sum _{i=1}^d \left[ \left[ { \prod \nolimits _{ j \in \{ 1,\dots ,d \} \backslash \{i\}} \Bigg ( (2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \Bigg ( - \frac{(x_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)}\Bigg ) \Bigg )}\right] \right. \nonumber \\{} & {} \qquad \cdot \biggl [\left( { \frac{\partial }{\partial t} \left( { (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} }\right) }\right) \, \exp \left( {- \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \nonumber \\{} & {} \qquad \left. + (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \left( { \frac{\partial }{\partial t} \left( { - \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)} }\right) }\right) \,\exp \left( {- \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \biggr ] \right] \nonumber \\{} & {} \quad = \sum _{i=1}^d \left[ \left[ { \prod \nolimits _{ j \in \{ 1, \dots ,d \} \backslash \{i\}} \left( { (2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(x_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)}}\right) }\right) }\right] \right. \nonumber \\{} & {} \qquad \left. \cdot \biggl [ - (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \left[ {\frac{\big ( \tfrac{\partial }{\partial t}\mathfrak {S}_i\big ) (t)}{2\mathfrak {S}_i(t)}}\right] \exp \left( {- \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \right. \nonumber \\{} & {} \qquad \left. + (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \biggl ( \frac{ 2\big ({\tfrac{\partial }{\partial t}\mathfrak {U}_{i}}\big )(t)(x_i-\mathfrak {U}_{i}(t))}{2\mathfrak {S}_i(t)} \right. \nonumber \\{} & {} \qquad \left. + \frac{(x_i-\mathfrak {U}_i(t))^2 \big ({\tfrac{\partial }{\partial t}\mathfrak {S}_i}\big )(t)}{2|{\mathfrak {S}_i(t)} |^{2}} \biggr ) \exp \left( {- \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \biggr ] \right] \nonumber \\{} & {} \quad = u(t,x) \left[ { \sum _{i=1}^d\left( { \frac{-\big ({\tfrac{\partial }{\partial t}\mathfrak {S}_i}\big ) (t)}{2\mathfrak {S}_i(t)} + \frac{ 2\mathfrak {S}_i(t) \big ({\tfrac{\partial }{\partial t}\mathfrak {U}_i}\big )(t)(x_i-\mathfrak {U}_{i}(t)) + (x_i-\mathfrak {U}_i(t))^2 \big ({\tfrac{\partial }{\partial t}\mathfrak {S}_i}\big )(t)}{2|{\mathfrak {S}_i(t)} |^{2}}}\right) }\right] .\nonumber \\ \end{aligned}$$

(193)

Moreover, observe that (187), the chain rule, and the product rule ensure that for every $i \in \{1, \dots ,d\}$, $t \in [0,\infty )$ it holds that

$$\begin{aligned} \begin{aligned} \big ({\tfrac{\partial }{\partial t}\mathfrak {U}_i}\big )(t)&= \frac{\partial }{\partial t} \left( { \frac{\mathfrak {m}_i \mathfrak {u}_i}{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)} }\right) \\&= - |{\mathfrak {m}_i} |^2 \mathfrak {u}_i \left[ { \frac{\mathfrak {m}_i \sinh (\mathfrak {m}_i t) + \mathfrak {s}_i \cosh (\mathfrak {m}_i t)}{\left[ { \mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)}\right] ^2} }\right] \\&= - \mathfrak {S}_i(t) \mathfrak {U}_i(t) \end{aligned} \end{aligned}$$

(194)

and

$$\begin{aligned} \begin{aligned}&\big ({\tfrac{\partial }{\partial t}\mathfrak {S}_i}\big )(t) \\&\quad = \frac{\partial }{\partial t} \left( { \mathfrak {m}_i \left[ { \frac{\mathfrak {m}_i \sinh (\mathfrak {m}_i t) + \mathfrak {s}_i \cosh (\mathfrak {m}_i t)}{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)}}\right] }\right) \\&\quad = |{\mathfrak {m}_i} |^2 \left[ { \frac{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)}{\mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)}}\right] - |{\mathfrak {m}_i} |^2\left[ { \frac{\mathfrak {m}_i \sinh (\mathfrak {m}_i t) + \mathfrak {s}_i \cosh (\mathfrak {m}_i t)}{ \mathfrak {m}_i \cosh (\mathfrak {m}_i t) + \mathfrak {s}_i \sinh (\mathfrak {m}_i t)} }\right] ^2 \\&\quad = |{\mathfrak {m}_i} |^2 - |{\mathfrak {S}_i(t)} |^2 . \end{aligned} \end{aligned}$$

(195)

Combining this with (193) implies that for every $i \in \{1, 2,\dots ,d\}$, $t \in [0,\infty )$ it holds that

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x)&= \frac{u(t,x)}{2} \sum _{i=1}^d\left[ \frac{-\big [{|{\mathfrak {m}_i} |^2 - |{\mathfrak {S}_i(t)} |^2}\big ]}{\mathfrak {S}_i(t)} \right. \nonumber \\&\quad \left. + \frac{ 2|{\mathfrak {S}_i(t)} |^2 \mathfrak {U}_i(t) (\mathfrak {U}_{i}(t) - x_i) + (x_i-\mathfrak {U}_i(t))^2 (|{\mathfrak {m}_i} |^2 - |{\mathfrak {S}_i(t)} |^2)}{|{\mathfrak {S}_i(t)} |^{2}}\right] \nonumber \\&= \frac{u(t,x)}{2} \sum _{i=1}^d\Biggl [ |{\mathfrak {m}_i} |^2 \left( { \bigg ({\frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)}}\bigg )^{2} - \frac{1}{\mathfrak {S}_i(t)} }\right) \nonumber \\&\quad + \mathfrak {S}_i(t) + 2\big (|{\mathfrak {U}_i(t)} |^2 - \mathfrak {U}_i(t)\, x_i\big ) - \big (|{x_i} |^2 -2 \mathfrak {U}_i(t) \, x_i + |{\mathfrak {U}_i(t)} |^2 \big ) \Biggr ] \nonumber \\&= \frac{u(t,x)}{2} \sum _{i=1}^d \left[ { |{\mathfrak {m}_i} |^2 \left( { \bigg ({\frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)}}\bigg )^{2} - \frac{1}{\mathfrak {S}_i(t)} }\right) + \mathfrak {S}_i(t) + |{\mathfrak {U}_i(t)} |^2 - |{x_i} |^2 }\right] . \end{aligned}$$

(196)

Furthermore, note that (191) and the product rule show that for every $i \in \{1,2, \dots ,d\}$, $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned} \big ({ \tfrac{\partial }{\partial x_i} u}\big )(t,x)&= \frac{\partial }{\partial x_i} \left[ \prod _{j = 1}^d\left[ {(2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(x_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)}}\right) }\right] \right] \\ {}&= \left[ { \frac{\partial }{\partial x_i} \left[ {(2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(x_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)} }\right) }\right] }\right] \\&\quad \cdot \prod _{ j \in \{ 1,2, \dots ,d \} \backslash \{i\}} \left[ { (2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(x_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)} }\right) }\right] \\ {}&= - u(t,x) \bigg ({ \frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)} }\bigg ) = u(t,x) \bigg ({ \frac{\mathfrak {U}_i(t) - x_i }{\mathfrak {S}_i(t)} }\bigg ) . \end{aligned} \end{aligned}$$

(197)

The product rule therefore assures that for every $i \in \{1,2, \dots ,d\}$, $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned}{} & {} \big ({ \tfrac{\partial ^2 }{\partial x_i^2} u }\big )(t,x) = \frac{\partial }{\partial x_i} \left( {u(t,x) \bigg ({ \frac{ \mathfrak {U}_i(t) - x_i}{\mathfrak {S}_i(t)} }\bigg )}\right) \nonumber \\{} & {} \quad = \big ({\tfrac{\partial }{\partial x_i} u}\big )(t,x)\bigg ({ \frac{\mathfrak {U}_i(t) - x_i }{\mathfrak {S}_i(t)} }\bigg ) - \frac{u(t,x)}{\mathfrak S_i(t)} = u(t,x) \left[ { \bigg ({\frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)}}\bigg )^{2} - \frac{1}{\mathfrak {S}_i(t)} }\right] .\nonumber \\ \end{aligned}$$

(198)

Hence, we obtain that for every $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^d \left[ { \tfrac{1}{2} |{\mathfrak {m}_i} |^2\big ({\tfrac{\partial ^2 }{\partial x_i^2} u}\big ) (t,x) }\right] = \frac{u(t,x)}{2} \sum _{i=1}^d \left[ { |{\mathfrak {m}_i} |^2 \left( { \bigg ({\frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)}}\bigg )^{2} - \frac{1}{\mathfrak {S}_i(t)} }\right) }\right] . \end{aligned} \end{aligned}$$

(199)

Next observe that (191) and Fubini’s theorem ensure that for every $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&u(t,x)\left( { a(x) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} }\right) \\&\quad = u(t,x) \left( { - \frac{1}{2} \left[ {\sum _{i=1}^d |{x_i} |^2 }\right] - \int _{\mathbb {R}^d} - \frac{1}{2} \left[ { \sum _{i=1}^d |{\textbf{x}_i} |^2 }\right] u(t,\textbf{x}) \, \textrm{d}\textbf{x} }\right) \\&\quad = \frac{u(t,x)}{2} \left( - \left[ {\sum _{i=1}^d |{x_i} |^2 }\right] \right. \\&\left. \quad \quad + \sum _{i=1}^d \biggl [ \int _\mathbb {R}|{\textbf{x}_i} |^2 \, (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(\textbf{x}_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \, \textrm{d}\textbf{x}_i \right. \\&\left. \quad \quad \cdot \bigg ({\prod \nolimits _{ j \in \{ 1,2, \dots ,d \} \backslash \{i\}} \int _\mathbb {R}(2\pi \mathfrak {S}_j(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(\textbf{x}_j -\mathfrak {U}_j(t) )^2}{2\mathfrak {S}_j(t)}}\right) \, \textrm{d}{\textbf{x}_j} }\bigg ) \biggr ] \right) . \end{aligned} \end{aligned}$$

(200)

This and the fact that for every $i \in \{1,2, \dots , d\}$, $t \in [0,\infty )$ it holds that

$$\begin{aligned} \int _\mathbb {R}(2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{( x -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \, \textrm{d}x = 1 \end{aligned}$$

(201)

imply that for every $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&u(t,x)\left( { a(x) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} }\right) \\&\quad = \frac{u(t,x)}{2} \sum _{i=1}^d \left[ {- |{x_i} |^2 + \int _\mathbb {R}|{\textbf{x}_i} |^2 \, (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{(\textbf{x}_i -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) \,\textrm{d}\textbf{x}_i }\right] . \end{aligned} \end{aligned}$$

(202)

Next observe that the integral transformation theorem demonstrates that for every $i \in \{1,2, \dots ,d\}$, $t \in [0,\infty )$ it holds that

$$\begin{aligned} \begin{aligned}&\int _\mathbb {R}x^2 \left[ { (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{( x -\mathfrak {U}_i(t) )^2}{2\mathfrak {S}_i(t)}}\right) }\right] \textrm{d}x \\&\quad = \int _\mathbb {R}(x + \mathfrak {U}_i(t))^2 \left[ { (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{x^2}{2\mathfrak {S}_i(t)}}\right) }\right] \textrm{d}x\\&\quad = \int _\mathbb {R}x ^2 \left[ { (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{x^2}{2\mathfrak {S}_i(t)}}\right) }\right] \textrm{d}x \\&\quad \quad + \int _\mathbb {R}|{\mathfrak {U}_i(t)} |^2 \left[ { (2\pi \mathfrak {S}_i(t))^{-\nicefrac {1}{2}} \exp \left( { - \frac{x^2}{2\mathfrak {S}_i(t)}}\right) }\right] \textrm{d}x \\&\quad = \mathfrak {S}_i(t) + |{\mathfrak {U}_i(t)} |^2 . \end{aligned} \end{aligned}$$

(203)

Combining this with (202) ensures that for every $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&u(t,x)\left( { a(x) - \int _{\mathbb {R}^d} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} }\right) = \frac{u(t,x)}{2} \sum _{i=1}^d \left( { \mathfrak {S}_i(t) + |{\mathfrak {U}_i(t)} |^2 - |{x_i} |^2 }\right) . \end{aligned} \end{aligned}$$

(204)

This and (199) demonstrate that for every $t \in [0,\infty )$, $x = (x_1, \dots ,x_d)\in \mathbb {R}^d$ it holds that

$$\begin{aligned} \begin{aligned}&u(t,x)\left( {a(x) - \int _{D} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} }\right) + \sum _{i=1}^{d} \tfrac{1}{2} |{\mathfrak {m}_i} |^2 \big ({\tfrac{\partial ^2 }{\partial x_i^2} u}\big ) (t,x) \\&\quad = \frac{u(t,x)}{2} \sum _{i=1}^d \left[ { |{\mathfrak {m}_i} |^2 \left( { \bigg ({\frac{x_i - \mathfrak {U}_i(t)}{\mathfrak {S}_i(t)}}\bigg )^{2} - \frac{1}{\mathfrak {S}_i(t)} }\right) + \mathfrak {S}_i(t) + |{\mathfrak {U}_i(t)} |^2 - |{x_i} |^2 }\right] . \end{aligned} \end{aligned}$$

(205)

Combining this with (196) proves item (iii). The proof of Lemma 5.2 is thus complete. $\square$

Machine-learning based approximations. Assume Framework 5.1, let $\mathcal D\subseteq \mathbb {R}^d$, $\mathfrak {m}_1,\mathfrak {m}_2,\dots ,\mathfrak {m}_d,\mathfrak {s}_1,\mathfrak {s}_2,\dots ,\mathfrak {s}_d,\mathfrak {u}_1, \mathfrak {u}_2, \dots ,\mathfrak {u}_d,\mathfrak t \in \mathbb {R}$ satisfy for every $k \in \{1,2,\dots ,d\}$ that $\mathfrak {m}_k = \tfrac{1}{10}$, $\mathfrak {s}_k = \tfrac{1}{20}$, $\mathfrak {u}_k = 0$, and $\mathfrak t=\tfrac{1}{50}$, assume $d\in \{1,2,5,10\}$, $D= \mathbb {R}^d$, $T\in \{\nicefrac 1{10},\nicefrac {1}{5},\nicefrac {1}{2}\}$, $N=10$, $K_1 = K_2 = \cdots = K_N= 1$, let $a\in C(\mathbb {R}^d,\mathbb {R})$, $\delta \in C(\mathbb {R}^d,(0,\infty ))$ satisfy for every $x \in \mathbb {R}^d$ that $a(x) = -\frac{1}{2}\Vert {x} \Vert ^2$, and assume for every $s,t \in [0,T]$, $v= (v_1,\dots ,v_d),\,x = (x_1,\dots ,x_d)\in \mathbb {R}^d$, $\textbf{x} \in \mathbb {R}^d$, $y,\textbf{y} \in \mathbb {R}$, $A\in \mathcal {B}(\mathbb {R}^d)$ that $\nu _x(A)=\int _{A\cap \mathcal D}\delta (\textbf{x})\,\textrm{d}\textbf{x}$, $g(x)= (2\pi )^{-\nicefrac {d}{2}}\big [{ \prod _{ i = 1 }^d |{\mathfrak {s}_i} |^{-\nicefrac {1}{2}}}\big ] \exp \big ({-\sum _{i = 1}^d \frac{(x_i - \mathfrak {u}_i )^2}{2\mathfrak {s}_i}}\big )$, $\mu (x)=(0,\dots ,0)$, $\sigma (x)v=(\mathfrak {m}_1 v_1, \dots , \mathfrak {m}_d v_d)$, $f(t,x,\textbf{x},y,\textbf{y}) = y(a(x)-\textbf{y a}(\textbf{x})[\delta (\textbf{x})]^{-1})$, and

$$\begin{aligned} H(t,s,x,v) = x + \mu (x)(t-s)+ \sigma (x)v = x+(\mathfrak m_1v_1,\dots ,\mathfrak m_dv_d) \end{aligned}$$

(206)

(cf. (139) and (150)). The solution $u:[0,T]\times \mathbb {R}^d \rightarrow \mathbb {R}$ of the PDE in (174) then satisfies that for every $t\in [0,T]$, $x = (x_1, \dots , x_d) \in \mathbb {R}^d$ it holds that

$$\begin{aligned} u(0,x)= (2\pi )^{-\nicefrac {d}{2}}\left[ { \prod _{ i = 1 }^d |{\mathfrak {s}_i} |^{-\nicefrac {1}{2}}}\right] \exp \bigg ({-\sum _{i = 1}^d \tfrac{(x_i - \mathfrak {u}_i )^2}{2\mathfrak {s}_i}}\bigg ) \end{aligned}$$

(207)

and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big ) (t,x) = u(t,x) \bigg ({a(x) - \int _\mathcal {D} u(t,\textbf{x})\, a(\textbf{x}) \, \textrm{d}\textbf{x} }\bigg ) + \sum _{i=1}^{d} \tfrac{1}{2} |{\mathfrak {m}_i} |^2 \left( {\tfrac{\partial ^2 }{\partial x_i^2} u}\right) (t,x) . \end{aligned}$$

(208)

For Table 4, we approximate for each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 15,\nicefrac 12,1\}$ the value $u(T,(0,\dots ,0))$ by computing 5 independent realizations of ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We report in Table 4 approximations of the mean and the standard deviation of this random variable as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error (see the discussion below Framework 5.1 for more details). For the latter two statistics, the reference value $u(T,(0,\ldots ,0))$ has been calculated using Lemma 5.2 above which provides an explicit representation of the exact solution of the PDE in (208).

Table 4 Numerical simulations for the approximation method in Framework 3.1 in the case of the replicator-mutator PDEs in (208) in Sect. 5.4 where we approximate the value of $u(T,(0,\dots ,0))$, assuming for every $n,m,j\in \mathbb {N}$, $\textbf{x}\in \mathbb {R}^d$ that $\mathcal D=\mathbb {R}^d$, $\xi ^{n,m,j}=0$, $\gamma _m = 10^{-3}$, $M_n=1000$, and $\delta (\textbf{x})=(2\pi )^{-\nicefrac d2}\mathfrak t^{-d}\exp \big ({-\tfrac{\Vert {\textbf{x}} \Vert ^2}{2\mathfrak t^2}}\big )$

Table 5 Numerical simulations for the approximation method in Framework 3.1 in the case of the replicator-mutator PDEs in (208) in Sect. 5.4 where we approximate the function $[-1,1]^d\ni x\mapsto u(T,x)\in \mathbb {R}$, assuming for every $n,m,j\in \mathbb {N}$, $\textbf{x}\in \mathbb {R}^d$ that $\mathcal D=[-1,1]^d$, $\xi ^{n,m,j}=0$, $\gamma _m = 10^{-2}\mathbb {1}_{[0,1000]}(m)+10^{-3}\mathbb {1}_{[1001,2000]}(m)$, $M_n=2000$, and $\delta (\textbf{x})=2^{-d}$

In Table 5 we report statistics on the capability of the approximation method in Framework 3.1 to approximate the solution of the PDE in (208) on an entire subset of the domain. More specifically, for Table 5, we approximate for each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 1{10},\nicefrac 15,\nicefrac 12\}$ the function $[-1,1]^d\ni x\mapsto u(T,x)\in \mathbb {R}$ by computing 5 independent realizations of $[-1,1]^d\ni x\mapsto {\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},x)\in \mathbb {R}$. We report in Table 4 an estimate of the $L^2$-approximation error

$$\begin{aligned} \mathbb {E}\Bigl [\textstyle \bigl (\int _{[-1,1]^d} |{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},x) - u(T,x)} |^2\,\textrm{d}x\bigr )^{\nicefrac 12}\Bigr ] \end{aligned}$$

(209)

and of the standard deviation

$$\begin{aligned}{} & {} \biggl (\mathbb {E}\biggl [ \Bigl ( \textstyle \bigl (\int _{[-1,1]^d} |{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},x) - u(T,x)} |^2\,\textrm{d}x\bigr )^{\nicefrac 12} - \mathbb {E}\Bigl [\textstyle \bigl (\int _{[-1,1]^d} |{{\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},x) - u(T,x)} |^2\,\textrm{d}x\bigr )^{\nicefrac 12}\Bigr ] \Bigr )^2 \biggr ]\biggr )^{\!\!\nicefrac 12}\nonumber \\ \end{aligned}$$

(210)

of the error. The integrals appearing in (209) and (210) have been computed by means of a standard Monte Carlo approximation using the exact solution of the PDE as provided by Lemma 5.2 above.

Fig. 3

Plot of a machine learning-based approximation of the solution of the replicator-mutator PDE in (208) in the case $d=5$, $T=\nicefrac 12$, and $\mathcal D=\mathbb {R}^d$. The left-hand side shows a plot of $[-\nicefrac {1}{4}, \nicefrac {1}{4}] \ni x \mapsto {\mathbb {V}}_n^{1,0}(\Theta ^n_{M_n}(\omega ),(x, 0, \dots ,0)) \in \mathbb {R}$ for $n\in \{0,1,2,3\}$ and one realization $\omega \in \Omega$ where the functions $\mathbb {R}^d\ni x\mapsto {\mathbb {V}}_n^{1,0}(\Theta ^n_{M_n}(\omega ),x)\in \mathbb {R}$ for $n\in \{0,1,2,3\}$, $\omega \in \Omega$ were computed via Framework 5.1 as an approximation of the solution of the PDE in (208) with $d=5$, $T=\nicefrac 12$, and $\mathcal D=[-\nicefrac 12,\nicefrac 12]^d$ where we take $M_1=M_2=\cdots =M_N=2000$, $\gamma _1=\gamma _2=\cdots =\gamma _{2000}=\nicefrac {1}{200}$, and $\delta =\mathbb {1}_{\mathbb {R}^d}$ and where we take $\xi ^{n,m,j}:\Omega \rightarrow \mathbb {R}^d$, $n, m, j \in \mathbb {N}$, to be independent $\mathcal {U}_{[-\nicefrac {1}{2},\nicefrac {1}{2}]^d}$-distributed random variables. The right-hand side of Fig. 3 shows a plot of $[-\nicefrac {1}{4}, \nicefrac {1}{4}] \ni x \mapsto u(t, (x, 0, \dots ,0)) \in \mathbb {R}$ for $t\in \{0,0.05,0.1,0.15\}$ where u is the exact solution of the PDE in (208) with $d=5$, $T=\nicefrac 12$, and $\mathcal D=\mathbb {R}^d$

Figure 3 provides a graphical illustration of an approximation to a solution of the PDEs in (208) computed by means of the the method in Framework 5.1 compared to the exact solution. More specifically, in Fig. 3 we use the machine learning-based method in Framework 5.1 to approximate the solution $u:[0,T]\times \mathbb {R}^d\rightarrow \mathbb {R}$ of the PDE in (208) above with $d=5$, $T=\nicefrac 12$, and $\mathcal D=\mathbb {R}^d$. The right-hand side of Fig. 3 shows a plot of $[-\nicefrac {1}{4}, \nicefrac {1}{4}] \ni x \mapsto u(t, (x, 0, \dots ,0)) \in \mathbb {R}$ for $t\in \{0,0.05,0.1,0.15\}$ where u is the exact solution of the PDE in (208) with $d=5$, $T=\nicefrac 12$, and $\mathcal D=\mathbb {R}^d$ computed via (188) in Lemma 5.2 below. The left-hand side of Fig. 3 shows a plot of $[-\nicefrac {1}{4}, \nicefrac {1}{4}] \ni x \mapsto {\mathbb {V}}_n^{1,0}(\Theta ^n_{M_n}(\omega ),(x, 0, \dots ,0)) \in \mathbb {R}$ for $n\in \{0,1,2,3\}$ and one realization $\omega \in \Omega$ where the functions $\mathbb {R}^d\ni x\mapsto {\mathbb {V}}_n^{1,0}(\Theta ^n_{M_n}(\omega ),x)\in \mathbb {R}$ for $n\in \{0,1,2,3\}$, $\omega \in \Omega$ were computed via Framework 5.1 as an approximation of the solution of the PDE in (208) with $d=5$, $T=\nicefrac 12$, and $\mathcal D=[-\nicefrac 12,\nicefrac 12]^d$. For the approximation, we take $M_1=M_2=\cdots =M_N=2000$, $\gamma _1=\gamma _2=\cdots =\gamma _{2000}=\nicefrac {1}{200}$, and $\delta =\mathbb {1}_{\mathbb {R}^d}$ and we take $\xi ^{n,m,j}:\Omega \rightarrow \mathbb {R}^d$, $n, m, j \in \mathbb {N}$, to be independent $\mathcal {U}_{[-\nicefrac {1}{2},\nicefrac {1}{2}]^d}$-distributed random variables. Note that the solution of the PDE in (208) in the case $\mathcal D=[-R,R]^d$ with $R\in (0,\infty )$ sufficiently large is a good approximation of the solution $u:[0,T]\times \mathbb {R}^d\rightarrow \mathbb {R}$ of the PDE in (208) in the case $\mathcal D=\mathbb {R}^d$ since we have that for every $t\in [0,T]$ the value u(t, x) of the solution u of the PDE in (208) in the case $\mathcal D=\mathbb {R}^d$ sufficiently quickly tends to 0 as $\Vert {x} \Vert$ tends to $\infty$.

MLP approximations.

For Table 6, we use the approximation method presented in Framework 4.1 to compute approximations of the PDEs in (208) by applying Example 4.5 with $\mathfrak m_1=\mathfrak m_2=\cdots =\mathfrak m_d=\frac{1}{10}$, $\mathfrak s_1=\mathfrak s_2=\cdots =\mathfrak s_d=\frac{1}{20}$, and $\mathfrak u_1=\mathfrak u_2=\cdots =\mathfrak u_d=0$. We compute 5 independent realizations of $U^{(0)}_{5,5,0,\infty }(0,(0,\dots ,0))$ as approximations of the value at (0, x) of the solution u of the PDE in (166) in Example 4.5 above (note that this is the value at $(T,x)\in [0,T]\times \mathbb {R}^d$ of the solution u of the PDE in (208) above; cf., e.g., Beck et al. [101, Remark 3.3]). Based on these realizations, we report in Table 6 approximations of the mean and the standard deviation of the random variable $U^{(0)}_{5,5,0,\infty }(0,(0,\dots ,0))$ as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error. For the latter two statistics, the reference value has been calculated using Lemma 5.2 above which provides an explicit representation of the exact solution of the PDE in (208) above (and hence of the exact solution of the PDE in (166) in Example 4.5 above).

Table 6 Numerical simulations for the approximation method in Framework 4.1 in the case of the replicator-mutator PDE in (208) in Sect. 5.4 (cf. Beck et al. [101, Remark 3.3] and Example 4.5 applied with $\mathfrak {m}_1\curvearrowleft \tfrac{1}{10}, \mathfrak {m}_2\curvearrowleft \tfrac{1}{10}, \dots ,\mathfrak {m}_d\curvearrowleft \tfrac{1}{10}, \mathfrak {s}_1\curvearrowleft \tfrac{1}{20}, \mathfrak {s}_2\curvearrowleft \tfrac{1}{20}, \dots , \mathfrak {s}_d\curvearrowleft \tfrac{1}{20}, \mathfrak {u}_1\curvearrowleft 0, \mathfrak {u}_2\curvearrowleft 0,\dots ,\mathfrak {u}_d\curvearrowleft 0$ )

Comparison of the two methods.

In Fig. 4 below we compare the performance of the machine learning-based approximation method in Framework 5.1 to the MLP approximation method in Framework 4.1 when computing approximations to the solution of the PDE in (208) with $d=5$, $\mathcal D=[-1,1]^d$, and $T=0.2$. A straightforward runtime comparison between these two methods is difficult, as the machine learning-based method is highly parallelizable, with our simulations running to a large part on the GPU, whereas the MLP approximation method cannot be parallelized as easily and in our simulations is performed entirely on the CPU. As a consequence, comparisons of the runtimes to a large degree reflect the relative performance of the GPU compared to the CPU of the test system. In Fig. 4 we instead use the number of evaluations of one-dimensional standard normal random variables as a proxy for the complexity and we plot this measure against the relative $L^1$-approximation error of the approximation method. For the MLP approximation method, we obtained the four different measurements by computing 5 realizations each of $U^{(0)}_{n,n,0,\infty }(0,(0,\dots ,0))$ for $n\in \{2,3,4,5\}$. For the machine learning-based approximation method in Framework 5.1, we similarly obtained the four different measurements by computing 5 realizations each of $\mathbb {V}^{1,0}_{N}(\Theta ^N_{M_N},(0,\dots ,0))$ varying the number of time steps (with $N\in \{1,2,3,4\}$), the number of neurons in each of the two hidden layers (with the number of neurons in each hidden layer chosen from $\{10, 20, 30, 40\}$), and the batch sizes (with $\forall \,k\in \mathbb {N}:J_k=J_1\in \{10^1,10^2,10^3,10^4\}$).

Fig. 4

Comparison of the machine learning-based method in Framework 3.1 and the MLP approximation method in Framework 2.10 when computing approximations to the solution of the PDE in (208) with $d=5$, $\mathcal D=[-1,1]^d$, and $T=0.2$

5.5 Allen–Cahn PDEs with conservation of mass

In this subsection we use the machine learning-based approximation method in Framework 5.1 to approximately calculate the solutions of certain Allen–Cahn PDEs with cubic nonlinearity, conservation of mass, and no-flux boundary conditions (cf., e.g., Rubinstein and Sternberg [10]).

Assume Framework 5.1, let $\epsilon \in (0,\infty )$ satisfy $\epsilon = \tfrac{1}{10}$, assume $d\in \{1,2,5,10\}$, $D= [-\nicefrac 12,\nicefrac 12]^d$, $T\in \{\nicefrac {1}{5},\nicefrac {1}{2},1\}$, $N=10$, $K_1 = K_2 = \cdots = K_N= 5$, and $M_1 = M_2 = \cdots = M_N = 500$, assume $\xi ^{n,m,j}, n, m, j \in \mathbb {N}$, are independent $\mathcal {U}_{D}$-distributed random variables, assume for every $m \in \mathbb {N}$ that $\gamma _m =10^{-2}$, and assume for every $s,t \in [0,T]$, $x,\textbf{x}\in D$, $y,\textbf{y} \in \mathbb {R}$, $v\in \mathbb {R}^d$, $A \in \mathcal {B}(D)$ that $\nu _x(A) = \int _A \textrm{d}\textbf{x}$, $g(x)= \exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$, $\mu (x)=(0, \dots , 0)$, $\sigma (x) v = \epsilon v$, $f(t,x,\textbf{x},y,\textbf{y})= y - y^3 - \big ( \textbf{y} - \textbf{y}^3\big )$, and

$$\begin{aligned} H(t,s,x,v) = R(x,x+\mu (x)(t-s)+\sigma (x)v) = R(x,x+\epsilon v) \end{aligned}$$

(211)

(cf. (139) and (150)). The solution $u:[0,T]\times D\rightarrow \mathbb {R}$ of the PDE in (174) then satisfies that for every $t\in (0,T]$, $x\in \partial _D$ it holds that $\langle {\textbf{n}(x) ,(\nabla _x u)(t,x)} \rangle = 0$ and that for every $t\in [0,T]$, $x\in D$ it holds that $u(0,x)=\exp (-\tfrac{1}{4}\Vert {x} \Vert ^2)$ and

$$\begin{aligned} \big ({\tfrac{\partial }{\partial t}u}\big )(t,x) = \tfrac{\epsilon ^2}{2} (\Delta _x u)(t,x) + u(t,x) - [u(t,x)]^3 - \int _{[-\nicefrac 12,\nicefrac 12]^d} u(t,\textbf{x}) - [u(t,\textbf{x})]^3 \,\textrm{d}\textbf{x} . \end{aligned}$$

(212)

Table 7 Numerical simulations for the approximation method in Framework 3.1 in the case of the Allen–Cahn PDEs with conservation of mass in (212) in Sect. 5.5

For each choice of $d\in \{1,2,5,10\}$ and $T\in \{\nicefrac 15,\nicefrac 12,1\}$ we approximate the unknown value $u(T,(0,\dots ,0))$ by computing 5 independent realizations of ${\mathbb {V}}^{1,0}_N(\Theta ^N_{M_N},(0,\ldots ,0))$. We report in Table 7 approximations of the mean and the standard deviation of this random variable as well as approximations of the relative $L^1$-approximation error and the uncorrected sample standard deviation of the approximation error (see the discussion below Framework 5.1 for more details). For the latter two statistics, the reference value which is used as an approximation for the unknown value $u(T,(0,\ldots ,0))$ of the exact solution of the PDE in (212) is computed via the MLP approximation method for non-local nonlinear PDEs in Framework 4.1 as described in Example 4.6 (cf. Beck et al. [101, Remark 3.3]). More precisely, we apply Example 4.6 with $d\in \{1,2,5,10\}$, $T\in \{\nicefrac 15, \nicefrac 12, 1\}$, $D=[-\nicefrac 12,\nicefrac 12]^d$ in the notation of Example 4.6 and we use the mean of 5 independent realizations of $U^{(0)}_{5,5,0,\infty }(0,(0,\dots ,0))$ as the reference value.

Fig. 5

Influence of various hyperparameters on the performance of the machine learning-based approximation method

5.6 Influence of hyperparameters

For both the machine learning-based approximation method and the MLP approximation method proposed above, several hyperparameters need to be chosen. More precisely, for the machine learning-based approximation method described in Framework 3.1, we need, e.g., to decide on the number of discrete time steps used in the approximation (denoted by $N\in \mathbb {N}$ in Framework 3.1 above), the numbers of samples used in the Monte Carlo approximation of the nonlocal term (denoted by $(K_n)_{n\in \mathbb {N}}\subseteq \mathbb {N}$ in Framework 3.1 above), the optimization algorithm used (represented by the functions $\Psi ^n_m:\mathbb {R}^\varrho \times \mathbb {R}^{\mathfrak d}\rightarrow \mathbb {R}^\varrho$, $n\in \{1,2,\dots ,N\}$, $m\in \mathbb {N}$, in Framework 3.1 above), the batch sizes used in the optimization algorithm (denoted by $(J_m)_{m\in \mathbb {N}}\subseteq \mathbb {N}$ in Framework 3.1 above), and the architecture of the employed neural networks (i.e., in the case of fully connected feedforward neural networks, the number of hidden layers and the number of neurons in each hidden layer). For the MLP approximation method introduced in Framework 4.1 above, we need, e.g., to decide on the numbers of samples used in the Monte Carlo approximation of the nonlocal term (denoted by $(K_{n,l,m})_{n,l,m\in \mathbb {N}_0}\subseteq \mathbb {N}$ in Framework 4.1 above) and which iteration to use as an approximation of the unknown PDE solution (i.e., for which $n,M\in \mathbb {N}_0$ to compute $U^{(0)}_{n,M,r_1,r_2}(t,x)$ in (159) in Framework 4.1 above).

In Figs. 5 and 6 we examine the influence of some of these choices on the accuracy and runtime of the proposed approximation methods when computing approximate solutions to the replicator-mutator PDEs in (208) where $d=5$, where $\mathcal D=[-1,1]^d$, and where for every $\textbf{x}\in \mathbb {R}^d$ it holds that $\delta (\textbf{x})=2^{-d}$. More specifically, in Fig. 5 we show the effect on the $L^1$-approximation error and on the runtime of the machine learning-based approximation method in Framework 5.1 when varying, respectively (from left to right and top to bottom), the number of samples used in the Monte Carlo approximation of the nonlocal term, the batch size, the number of time steps, the number of neurons in each of the hidden layers, and the number of hidden layers. In Fig. 6 we show the effect on the $L^1$-approximation error and on the runtime of the MLP approximation method in Framework 4.1 (cf. Example 4.5) when varying, respectively (from left to right), the number of samples used to compute the Monte Carlo approximation of the nonlocal term and the number of iteration steps.

Fig. 6

Influence of various hyperparameters on the performance of the MLP approximation method