Convergence of Hyperbolic Neural Networks Under Riemannian Stochastic Gradient Descent

Abstract

We prove, under mild conditions, the convergence of a Riemannian gradient descent method for a hyperbolic neural network regression model, both in batch gradient descent and stochastic gradient descent. We also discuss a Riemannian version of the Adam algorithm. We show numerical simulations of these algorithms on various benchmarks.

1 Introduction

In machine learning, we routinely encode data as vectors in the Euclidean space. However, some data have a latent geometric structure which is not suited to Euclidean embedding, and instead can be represented more faithfully in other geometries. In particular, hyperbolic embeddings have recently gained momentum, especially for data with latent hierarchical or tree-like structure, like synonym or type hierarchies [3]. Just as ordinary neural networks can be used to interpolate functions of data in the Euclidean space, a hyperbolic neural network can be used to interpolate functions on data embedded in the hyperbolic space.

Hyperbolic feed-forward neural networks, or HFFNNs, were introduced in [4], and generalizations to Riemannian manifolds for common training methods like the gradient descent were introduced in [1, 2]. It is known that HFFNNs can outperform conventional FFNNs on some problems such as textual entailment and noisy-prefix recognition [4], and a universal approximation theorem for HFFNNs was proved in [6]. However, little is known about their convergence under the gradient descent.

In this paper, we show that under natural conditions, the training of an HFFNN under Riemannian gradient descent will indeed converge. We also present numerical results of training a network under Riemannian gradient descent versus Riemannian Adam (RAdam), showing that it provides the accelerated convergence in practice. Previous papers have examined only networks of limited depth or which are fully linear, while our result applies to nonlinear HFFNNs of arbitrary depth, in exchange for requiring an adaptive step size to be computed at each iteration of training.

2 Background

2.1 Hyperbolic Neural Networks

Here we summarize some facts about gyrovector spaces and hyperbolic neural networks which we will need for our main result. A more complete introduction of hyperbolic neural networks can be found in [4], and of gyrovector spaces in [12].

The hyperbolic space, denoted as ${\mathbb {D}}_{c}^n$, can be modeled in several ways. We use the Poincaré ball model, which is the Riemannian manifold $({\mathbb {D}}^n_c,g^{{\mathbb {D}}})$ where

$$\begin{aligned} {\mathbb {D}}^n_c= & {} \{x\in {\mathbb {R}}^n{:} \; c||x||^2<1\}, \\ g_x^{{\mathbb {D}}}= & {} (\lambda ^c_x)^2{\textbf {I}}_n, \text { where }\lambda ^c_x=2/(1-c||x||^2). \end{aligned}$$

This model has the benefit of being conformal to the Euclidean space, as well as allowing us to use the closed-form expressions from [4] for certain operations. Other models have advantages of their own. In particular, the Lorentz half-sheet model can avoid the numerical instability that is encountered in the Poincaré model [11].

In ${\mathbb {R}}^n$ considered as a Riemannian manifold, vector addition can be written as $x+y=\exp ^c_x(P_{0\rightarrow x}\log ^c_0(y))$, where $P_{0\rightarrow x}$ is the parallel transport from 0 to x—this is simply the “tip-to-tail” method of vector addition often taught to students, restated in the language of manifolds. Analogously, we can define the operation of Möbius addition in ${\mathbb {D}}^n_c$ by $x\oplus _c y=\exp ^c_x(P_{0\rightarrow }\log ^c_0(y))$, where now the parallel transport is taken along the Levi-Civita connection of ${\mathbb {D}}^n_c$. This can be computed explicitly by

$$\begin{aligned} x\oplus _c y=\frac{(1+2c\langle x,y\rangle +c||y||^2)x +(1-c||x||^2)y}{1+2c\langle x,y\rangle +c^2||x||^2||y||^2}. \end{aligned}$$

Note in particular that $x\oplus _c y$ is a rational function in the coordinates of x and y, and by Cauchy-Schwarz the denominator is nonvanishing in ${\mathbb {D}}^n_c$, so gyrovector addition is smooth, a fact which we will use later.

Analogously we can define Möbius scalar multiplication by

$$\begin{aligned} r\otimes _c x=\exp ^c_0(r\log ^c_0(x)), \end{aligned}$$

and ${\mathbb {D}}^n_c$ equipped with the operations $\oplus _c,\otimes _c$ is called a gyrovector space. More generally, given any function $f{:}\;{\mathbb {R}}^n\rightarrow {\mathbb {R}}^m$, we can define its Möbius version $f^{\otimes _c}{:}\;{\mathbb {D}}^n_c\rightarrow {\mathbb {D}}^m_c$ by

$$\begin{aligned} f^{\otimes _c}(x)=\exp ^c_0(f(\log ^c_0(x))). \end{aligned}$$

In particular, we will discuss the Möbius version of an activation function $\sigma$ and of a matrix W acting as a linear map, which we denote by $\sigma ^{\otimes _c}$ and $W^{\otimes _c}$, respectively. Since we are working in the Poincaré ball model, we may use the coordinates of the model to unambiguously identify linear maps with matrices, so henceforth we will not mention the distinction.

With these definitions in hand, a hyperbolic neural network layer with the weight matrix W, the bias b, and the activation function $\sigma$ is given by $x\mapsto \sigma ^{\otimes _c}(W^{\otimes _c} x\oplus _c b)$, analogous to a Euclidean network layer $x\mapsto \sigma (Wx+b)$, and a network f of k hidden layers of $n_i$ neurons is given by

$$\begin{aligned} f(x)&=f_k\circ f_{k-1}\circ \cdots \circ f_2\circ f_1(x),\nonumber \\ f_i(x)&=\sigma _i^{\otimes _c}(W_i^{\otimes _c}x \oplus _c b_i),\quad 1 \leqslant i \leqslant k, \end{aligned}$$

(1)

such a network has parameters ${\textbf {W}}=(W_1,b_1,\cdots ,W_k,b_k)$ with $W_i\in {\mathbb {R}}^{n_i\times n_{i-1}}$, $b_i\in {\mathbb {D}}^{n_i}_{c}$. Euclidean and hyperbolic layers can be used in sequence by applying $\log ^c_0$ or $\exp ^c_0$ to move from ${\mathbb {D}}_{c}^n$ to ${\mathbb {R}}^n$ or vice versa, respectively. Note that unlike the Euclidean case, an HFFNN is always nonlinear, and thus a non-identity activation function is not strictly necessary to fit nonlinear data and may not even improve the performance.

2.2 Riemannian Training

Stochastic gradient descent, or SGD, is perhaps the most straightforward way to train a model. Although the use of the Poincaré ball model allows us to embed ${\mathbb {D}}_{c}^n$ into ${\mathbb {R}}^n$ and thus we could compute a gradient in the Euclidean sense, this is not geometrically meaningful, and can behave badly near the boundary. In fact, an ordinary gradient update could even send the bias outside ${\mathbb {D}}^n_c$, which is clearly undesirable. Bonnabel [2] introduced the algorithm of Riemannian stochastic gradient descent, or RSGD, to address this problem on a Riemannian manifold. Analogous to gradient descent in ${\mathbb {R}}^n$ which proceeds by $w_{t+1}=w_t -\gamma _t\nabla {\mathcal {L}}({\textbf {X}}_t,w_t)=\exp ^c_{w_t} (-\gamma _t\nabla {\mathcal {L}}({\textbf {X}}_t,w_t))$ where ${\textbf {X}}_t$ is the stochastically chosen sample from the dataset ${\textbf {X}}$ and $\nabla {\mathcal {L}}$ is the gradient in the calculus sense, the RSGD proceeds by

$$\begin{aligned} w_{t+1}=\exp ^c_{w_t}(-\gamma _t{{\,\textrm{grad}\,}}{\mathcal {L}}({\textbf {X}}_t,w_t)), \end{aligned}$$

(2)

where ${{\,\textrm{grad}\,}}{\mathcal {L}}$ is the gradient as a vector field on the manifold. Naturally, we require the samples to be chosen in such a way that ${\mathcal {L}}({\textbf {X}},w)={\mathbb {E}}[{\mathcal {L}} ({\textbf {X}}_t,w)]$.

A common modification of gradient descent is to implement momentum, which can accelerate the convergence and help escape saddle points. The Adam algorithm [5] uses momentum as a second-moment estimate. Bécigneul and Ganea [1] generalized these algorithms to Riemannian manifolds as well, interpreting Adam’s adaptivity in each coordinate as the adaptivity in the components of a product of manifolds. This is well-suited to our approach, since training a hyperbolic neural network with m layers of sizes $n_1,\cdots ,n_m$ is precisely an optimization problem on a product manifold of the form ${\mathbb {R}}^{n_1\times n_0}\times {\mathbb {D}}_{c}^{n_1}\times \cdots \times {\mathbb {R}}^{n_m\times n_{m-1}}\times {\mathbb {D}}_{c}^{n_m}.$ We restate these algorithms below, alongside the Euclidean versions for comparison.

As in Euclidean training, it is often helpful to examine whether a Riemannian gradient is Lipschitz. We use a generalization of the notion of a Lipschitz vector field, introduced in [9].

Definition 1

A function $f{:}\;(M,g)\rightarrow {\mathbb {R}}$ is said to have C-Lipschitz gradient if for any two points $a,b\in M$,

$$\begin{aligned} {|}{{\,\textrm{grad}\,}}f(b)-P_{a\rightarrow b}{{\,\textrm{grad}\,}}f(a)|_g \leqslant C{{\,\textrm{dist}\,}}_M(a,b). \end{aligned}$$

As one would hope, a Lipschitz Riemannian gradient guarantees that a sufficiently small step size will cause the loss to decrease, as shown in the following proposition.

Proposition 1

Let $f{:}\;M\rightarrow {\mathbb {R}}$ be a differentiable function on a manifold M, and denote the Levi-Civita connection by $P_{a\rightarrow b}$. If f has C-Lipschitz gradient in the above sense, then $f(b)-f(a)\leqslant \langle {{\,\textrm{grad}\,}}f(a),\log _a(b)\rangle _g+\frac{C}{2}{{\,\textrm{dist}\,}}(a,b)^2.$

Proof

Let $\gamma {:}\;[0,1]\rightarrow M$ be the geodesic curve from a to b. (Note that in general, such paths are not unique, but on the manifolds under consideration in this paper, they are.)

$$\begin{aligned} f(b)-f(a)&=\int _\gamma \,{{\,\textrm{grad}\,}}f \text { by the fundamental theorem of line integrals}\\&=\int _0^1\langle {{\,\textrm{grad}\,}}f(\gamma (t)),\gamma^{ \prime}(t)\rangle _g\,\textrm{d}t\\&=\int _0^1\langle P_{a\rightarrow \gamma (t)}{{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(t)\rangle _g\,\textrm{d}t\\&\quad +\int _0^1\langle {{\,\textrm{grad}\,}}f(\gamma (t))-P_{a\rightarrow \gamma (t)} {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(t)\rangle _g\,\textrm{d}t\\&=\int _0^1\langle {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(0)\rangle _g\,\textrm{d}t +\int _0^1\langle {{\,\textrm{grad}\,}}f(\gamma (t))-P_{a\rightarrow \gamma (t)} {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(t)\rangle _g\,\textrm{d}t\\ &\hspace{-45pt}\text { since}\ \gamma \ \text {a geodesic and} \ P_{a\rightarrow \gamma (t)}\ \text {metric-preserving}\\&=\langle {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(0)\rangle _g\cdot \text {length}(\gamma )\\&\quad +\int _0^1\langle {{\,\textrm{grad}\,}}f(\gamma (t))-P_{a\rightarrow \gamma (t)} {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(t)\rangle _g\,\textrm{d}t\\&=\langle {{\,\textrm{grad}\,}}f(a),\log _a(b)\rangle _g+\int _0^1 \langle {{\,\textrm{grad}\,}}f(\gamma (t))-P_{a\rightarrow \gamma (t)} {{\,\textrm{grad}\,}}f(a),\gamma ^{ \prime}(t)\rangle _g\,\textrm{d}t\\&\leqslant \langle {{\,\textrm{grad}\,}}f(a),\log _a(b)\rangle _g +\int _0^1 |{{\,\textrm{grad}\,}}f(\gamma (t))-P_{a\rightarrow \gamma (t)} {{\,\textrm{grad}\,}}f(a)|_g|\gamma ^{ \prime}(t)|_g\,\textrm{d}t\\&\leqslant \langle {{\,\textrm{grad}\,}}f(a),\log _a(b)\rangle _g +\int _0^1 C{{\,\textrm{dist}\,}}(a,\gamma (t))|\gamma ^{ \prime}(t)|_g\,\textrm{d}t\\&=\langle {{\,\textrm{grad}\,}}f(a),\log _a(b)\rangle _g+\frac{C}{2}{{\,\textrm{dist}\,}}(a,b)^2. \end{aligned}$$

In particular, in RGD since $w_{t+1}=\exp _{w_t}(-\gamma _t{{\,\textrm{grad}\,}}f(w_t)),$ the distance is ${{\,\textrm{dist}\,}}(w_{t+1},w_t)=\gamma _t|{{\,\textrm{grad}\,}}f(w_t)|_g$, so we obtain

$$\begin{aligned} f(w_{t+1})-f(w_t)& \leqslant \langle {{\,\textrm{grad}\,}}f(w_t), -\gamma _t{{\,\textrm{grad}\,}}f(w_t)\rangle _g +\frac{C}{2}|\gamma _t{{\,\textrm{grad}\,}}f(w_t)|^2_g\nonumber \\&=\left( -\gamma _t+\frac{C}{2}\gamma _t^2\right) |{{\,\textrm{grad}\,}}f(w_t)|^2_g. \end{aligned}$$

(3)

From this, we recover the familiar condition that if $\gamma _t<\frac{2}{C}$, then $f(w_{t+1})<f(w_t)$.

3 Convergence of HFFNNs Under RSGD

An HFFNN layer has two kinds of parameters: the weight matrix W, which is an ordinary $m\times n$ matrix, and the bias b which is a gyrovector in the Poincaré ball. As such, the gradient descent must be performed in a hybrid fashion. The weights are Euclidean and thus can be updated in the usual fashion, but since the biases are in the hyperbolic space rather than ${\mathbb {R}}^n$, we use the RSGD. This hybrid gradient descent scheme is equivalent to the RSGD on the product manifold $\prod _{i=1}^n{\mathbb {R}}^{n_{i+1}\times n_i}\times {\mathbb {D}}_{c}^{n_{i+1}}$, and so we will consider this unified interpretation.

We will show that an HFFNN converges under the RGD or the RSGD using any $C^2$ activation functions.¹ We rely on the following theorem from [2].

Theorem

(Bonnabel 2013) Assume that

$$\begin{aligned} \sum \gamma _t^2<\infty ,\sum \gamma _t=\infty . \end{aligned}$$

Suppose there exists a compact set K such that $w_t\in K$ for all $t \geqslant 0$, and that the gradient of the loss ${{\,\textrm{grad}\,}}{\mathcal {L}}$ is bounded on K. Then under the RSGD, the loss ${\mathcal {L}}(w_t)$ converges almost surely, and ${{\,\textrm{grad}\,}}{\mathcal {L}}(w_t)$ converges almost surely to zero.

It is worth noting that, because this theorem is so general, it gives only a weak notion of the convergence, and in particular does not guarantee that the weights themselves converge to any sort of critical point.

Theorem 1

Consider an HFFNN of arbitrarily many layers as described above, with loss given by

$$\begin{aligned} {\mathcal {L}}({\textbf {X}},{\textbf {W}}) =\frac{1}{k}\sum _{x\in {\textbf {X}}}(f(x; \;{\textbf {W}})-y_i)^2 +\lambda |{\textbf {W}}|_2^2 \end{aligned}$$

(4)

for the dataset ${\textbf {X}}$ and parameters ${\textbf {W}}$, with any $C^2$ activation functions. Let $C_p$ denote the local Lipschitz constant of ${\mathcal {L}}$ on the ball of radius 1 around p established in Lemma 1. If we select the step size by

$$\begin{aligned} \gamma _t \leqslant \min \left( \frac{2}{C_{{\textbf {W}}_{t-1}}}, \frac{1}{|{{\,\textrm{grad}\,}}_{{\textbf {W}}} {\mathcal {L}}({\textbf {X}}, {\textbf {W}}_{t-1})|_g},\frac{1}{t}\right) \end{aligned},$$

then under non-stochastic Riemannian gradient descent, the loss ${\mathcal {L}}({\textbf {W}}_t)$ converges, and its gradient converges to 0.

Proof

The loss has locally Lipschitz gradient by Lemma 1, so by (dynamically) selecting a sufficiently small step size—small enough to not leave a compact neighborhood of the current parameters (say, a ball of radius 1, which $\gamma _t \leqslant \frac{1}{{{\,|\textrm{grad}\,}}{\mathcal {L}} ({\textbf {X}}_t,{\textbf {W}}_{t-1})|_g}$ is sufficient to guarantee), and smaller than $2/C_t$ where $C_t$ is the local Lipschitz constant on this ball—we can guarantee that the loss decreases at each step by (3). Furthermore, we restrict these step sizes $\gamma _t$, so that $\gamma _t \leqslant 1/t$, which enforces the condition that $\sum \gamma _t^2<\infty$. If $\sum \gamma _t<\infty$ as well, then the weights converge absolutely, which gives us an even better result than expected.

Otherwise $\sum \gamma _t=\infty$ and we are in the case examined by [2]. In this case, the sequence of loss values is decreasing and in particular is bounded. Thanks to its $L^2$ regularization term, the loss ${\mathcal {L}}$ is coercive, so the sequence of weights is also bounded, and in particular they lie in a compact set, and since ${\mathcal {L}}$ is smooth, it is certainly bounded on this set. By the theorem of Bonnabel from [2], the loss converges and the gradient of the loss converges to zero.

Theorem 2

Consider an HFFNN as in Theorem 1, with the stochastic objective function ${\mathcal {L}}_\theta$ satisfying ${\mathbb {E}}_\theta [{\mathcal {L}}_\theta ]={\mathcal {L}}$. Let $C^\theta _{{\textbf {W}}_{t-1}}$ be the local Lipschitz constant of ${\mathcal {L}}_\theta$ in the unit ball around ${\textbf {W}}_{t-1}$. If the step size $\gamma _t$ is selected to satisfy

$$\begin{aligned} \gamma _t \leqslant \min \left( \frac{2}{C^\theta _{{\textbf {W}}_{t-1}}}, \frac{1}{|{{\,\textrm{grad}\,}}_{{\textbf {W}}} {\mathcal {L}}_\theta ({\textbf {X}},{\textbf {W}}_{t-1})|_g}, \frac{1}{t}\right) , \end{aligned}$$

then under RSGD, the loss ${\mathcal {L}}({\textbf {W}}_t)$ converges almost surely, and the gradient of the loss converges almost surely to zero.

Proof

Again by (3) above, we see that for any fixed $\theta$, we must have ${\mathcal {L}}_{\theta }({\textbf {X}},{\textbf {W}}_{t+1})\leqslant {\mathcal {L}}_{\theta }({\textbf {X}},{\textbf {W}}_t)$, and thus

$$\begin{aligned} {\mathcal {L}}({\textbf {X}},{\textbf {W}}_{t+1})={\mathbb {E}}_\theta [{\mathcal {L}}_\theta ({\textbf {X}},{\textbf {W}}_{t+1})] \leqslant {\mathbb {E}}_\theta [{\mathcal {L}}_\theta ({\textbf {X}},{\textbf {W}}_t)]={\mathcal {L}}({\textbf {X}},{\textbf {W}}_t). \end{aligned}$$

This shows that ${\mathcal {L}}({\textbf {X}},{\textbf {W}}_t)$ is decreasing, and thus the same argument as in Theorem 1 above goes through.

Lemma 1

If the activation functions $\sigma _i$ are $C^2$, then the loss function ${\mathcal {L}}$ (4) has a locally Lipschitz gradient.

Proof

Denote $M=\prod _{i=1}^n{\mathbb {R}}^{n_{i+1}\times n_i}\times {\mathbb {D}}_{c}^{n_{i+1}}$, the Riemannian manifold containing the parameters of the network. Let $K\subset \prod _{i=1}^n{\mathbb {R}}^{n_{i+1}\times n_i}\times {\mathbb {D}}_{c}^{n_{i+1}}$ be a compact set, and without loss of generality, a rectangle (i.e., $K=\prod _{i=1}^n R_i\times H_i$, for some compact sets $R_i\subset {\mathbb {R}}^{n_{i+1}\times n_i}$ and $H_i\subset {\mathbb {D}}_{c}^{n_{i+1}}$). We will work in the standard coordinates for the Poincaré ball. As before, we use $\nabla$ to denote the gradient in the calculus sense, while ${{\,\textrm{grad}\,}}$ denotes the gradient in the manifold sense, and similarly we will use $||\cdot ||$ to denote the Euclidean norm when identifying a tangent space of ${\mathbb {D}}_{c}^n$ with ${\mathbb {R}}^n$.

Since we are performing gradient descent on the product manifold M, it will be helpful to consider the gradients separately with respect to the weight matrices $W^i\in {\mathbb {R}}^{n_{i+1}\times n_i}$ and the biases $b^i\in {\mathbb {D}}_{c}^{n_i}$. Specifically, by Proposition 1, we have

$$\begin{aligned} {{\,\textrm{grad}\,}}{\mathcal {L}}=({{\,\textrm{grad}\,}}_{W^1}{\mathcal {L}},{{\,\textrm{grad}\,}}_{b^1}{\mathcal {L}}, \cdots ,{{\,\textrm{grad}\,}}_{W^n}{\mathcal {L}},{{\,\textrm{grad}\,}}_{b^n}{\mathcal {L}}). \end{aligned}$$

Furthermore, recall that on a product manifold $N=\prod N_i$, $|v|_{g_N}=\sqrt{\sum |v|^2_{g_i}}$ where $g_i$ is the metric in the component $N_i$, and likewise that ${{\,\textrm{dist}\,}}_N(a,b)=\sqrt{\sum {{\,\textrm{dist}\,}}_{N_i}(a_i,b_i)^2}$. Note in particular that this implies that for any i,

$$\begin{aligned} {{\,\textrm{dist}\,}}_{N_i}(a_i,b_i)\leqslant{{\,\textrm{dist}\,}}_N(a,b). \end{aligned}$$

(5)

It is elementary that if each of a family of functions $f_i$ are $C_i$-Lipschitz, respectively, then $\sqrt{\sum f_i^2}$ is $\sqrt{\sum C_i^2}$-Lipschitz, so we will show that the components of the gradient are each locally Lipschitz on their respective components of the product to show that the entire gradient is Lipschitz as well.

For a bias component $b_i^t\in {\mathbb {D}}_{c}^{n_i}$ at the iteration t, we can write down the following:

$$\begin{aligned}&\quad|{{\,\textrm{grad}\,}}_{b_i} {\mathcal {L}}(b_i^{t+1})-P_{b_i^t\rightarrow b_i^{t+1}} {{\,\textrm{grad}\,}}_{b_i} {\mathcal {L}}(b_i^t)|_{g(b_i^{t+1})}\\& =(\lambda ^c_{b_i^{t+1}})^2||(\lambda ^c_{b_i^{t+1}})^{-2} \nabla _{b_i} {\mathcal {L}}(b_i^{t+1})-P_{b_i^t\rightarrow b_i^{t+1}} (\lambda ^c_{b_i^t})^{-2}\nabla _{b_i} {\mathcal {L}}(b_i^t)||\\& \leqslant (\lambda ^c_{b_i^{t+1}})^2 \Big [||(\lambda ^c_{b_i^{t+1}})^{-2} \nabla _{b_i} {\mathcal {L}}(b_i^{t+1}) -(\lambda ^c_{b_i^{t+1}})^{-2}\nabla _{b_i} {\mathcal {L}}(b_i^t)||\\& \quad +||(\lambda ^c_{b_i^{t+1}})^{-2}\nabla _{b_i} {\mathcal {L}} (b_i^t)-(\lambda ^c_{b_i^t})^{-2}\nabla _{b_i} {\mathcal {L}}(b_i^t)||\\&\quad +||(\lambda ^c_{b_i^t})^{-2}\nabla _{b_i}{\mathcal {L}}(b_i^t) -P_{b_i^t\rightarrow b_i^{t+1}}(\lambda ^c_{b_i^t})^{-2} \nabla _{b_i} {\mathcal {L}}(b_i^t)||\Big ]\\& =||\nabla _{b_i} {\mathcal {L}}(b_i^{t+1}) -\nabla _{b_i} {\mathcal {L}}(b_i^t)||+\left| 1 -\left( \frac{\lambda ^c_{b_i^{t+1}}}{\lambda ^c_{b_i^t}} \right) ^2\right| ||\nabla _{b_i}{\mathcal {L}}(b_i^t)||\\&\quad +\left( \frac{\lambda ^c_{b_i^{t+1}}}{\lambda ^c_{b_i^t}} \right) ^2|I-P_{b_i^t\rightarrow b_i^{t+1}}|\,||\nabla _{b_i} {\mathcal {L}}(b_i^t)||. \end{aligned}$$

We will control these three terms. By compactness, on $H_i$, the Euclidean and hyperbolic distances differ by at most a constant factor $C_1$. Together with (5), it thus suffices to bound these quantities by a multiple of $||b_i^{t+1}-b_i^t||$, since

$$\begin{aligned} ||b_i^{t+1}-b_i^t||\leqslant C_1{{\,\textrm{dist}\,}}_{{\mathbb {D}}_{c}^n}(b_i^{t+1},b_i^t) \leqslant {{\,\textrm{dist}\,}}_M({\textbf {W}}_{t+1},{\textbf {W}}_t). \end{aligned}$$

First recall that the Möbius addition is given by

$$\begin{aligned} x\oplus _c y=\frac{(1-2c\langle x,y\rangle +c||y||^2)x +(1-c||x||^2)y}{1+2c\langle x,y\rangle +c^2||x||^2||y^2||}, \end{aligned}$$

which is a rational function in the components of x and y, and so it is smooth except at its poles. Moreover, by Cauchy-Schwarz, the denominator is nonvanishing when $||x||<1/\sqrt{c}$ and $||y||<1/\sqrt{c}$. Thus, the Möbius addition is smooth on the Poincaré ball. Also, by Lemma 2 from [4], we have

$$\begin{aligned} \exp ^c_x(v)= & {} x\oplus _c\left( \tanh \left( \sqrt{c} \frac{\lambda ^c_x||v||}{2}\right) \frac{v}{\sqrt{c}||v||}\right), \\ \log ^c_x(y)= & {} \frac{2}{\sqrt{c}\lambda ^c_x}\tanh ^{-1} (\sqrt{c}||-x\oplus _c y||)\frac{-x\oplus _c y}{||-x\oplus _c y||}, \end{aligned}$$

which are smooth as well. Inspecting (1) and (4), and since $W^{\otimes _c} x=\exp ^c_0(W\log ^c_0(x))$, we see that ${\mathcal {L}}$ is written as compositions of these functions and the $C^2$ activation functions $\sigma _i$, plus a smooth regularization term, and so ${\mathcal {L}}$ is $C^2$ on ${\mathbb {D}}_{c}^{n_i}$. Thus, its Hessian (in the calculus sense) is continuous and thus bounded on compact sets, so $\nabla {\mathcal {L}}$ is locally $C_2$-Lipschitz in the Euclidean sense for some constant $C_2$. Thus, we obtain a control on the first term by

$$\begin{aligned} ||\nabla _{b_i} {\mathcal {L}}(b_i^{t+1})-\nabla _{b_i} {\mathcal {L}}(b_i^t)|| \leqslant C_2||b_i^{t+1}-b_i^t|| .\end{aligned}$$

Now since $\lambda ^c_x=\frac{2}{1-c||x||^2}$, the coefficient of the second term can be rewritten as

$$\begin{aligned} 1-\left( \frac{\lambda ^c_{b_i^{t+1}}}{\lambda ^c_{b_i^t}}\right) ^2&=1-\frac{1-c||b_i^t||^2}{1-c||b_i^{t+1}||^2}\\&=\frac{c||b_i^t||^2-c||b_i^{t+1}||^2}{1-c||b_i^{t+1}||^2}\\&=\frac{c||b_i^t||+c||b_i^{t+1}||}{1-c||b_i^{t+1}||^2} (||b_i^t||-||b_i^{t+1}||)\\& \leqslant C_3||b_i^{t+1}-b_i^t||, \end{aligned}$$

where $C_3$ is a bound on the coefficient term in $H_i$ since it is continuous.

For the third term, by the continuity we immediately can bound

$$\begin{aligned} \left( \frac{\lambda ^c_{b_i^{t+1}}}{\lambda ^c_{b_i^t}}\right) ^2|| \nabla _{b_i}{\mathcal {L}}(b_i^t)|| \leqslant C_4 \end{aligned}$$

on $H_i$, so we turn our attention to the remaining factor $|I-P_{b_i^t\rightarrow b_i^{t+1}}|$. Since parallel transport along the Levi-Civita connection is metric preserving, we can write $P_{b_i^t\rightarrow b_i^{t+1}}=\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}U$ for U a rotation. Then we decompose

$$\begin{aligned} |I-P_{b_i^t\rightarrow b_i^{t+1}}|&=\left| I-\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}U\right| \\& \leqslant \left| I-\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}I\right| +\left| \frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}I -\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}U\right| \\&=\left( 1-\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}\right) +\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}|I-U|. \end{aligned}$$

Analogous to the above, on $H_i$ we have

$$\begin{aligned}{} & {} 1-\frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}} =\frac{c||b_i^{t+1}||^2-c||b_i^t||^2}{1-c||b_i^t||^2} \leqslant C_5||b_i^{t+1}-b_i^t||,\\{} & {} \frac{\lambda ^c_{b_i^t}}{\lambda ^c_{b_i^{t+1}}}\leqslant C_6. \end{aligned}$$

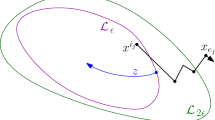
As we said, U is a rotation. The geodesic through $b_i^t$ and $b_i^{t+1}$ is an arc of a circle, which crosses the boundary perpendicularly, and so the center of this circle is outside the unit ball. In particular, if r is the radius of this circle, then $r>d={{\,\textrm{dist}\,}}_{{\mathbb {R}}^{n_i}}(H_i,\partial {\mathbb {D}}_{c}^{n_i})$. The angle $\theta$ by which U rotates is precisely the central angle of the arc $\widehat{b_i^t b_i^{t+1}}$ (see Fig. 1). For any unit vector x, we have

$$\begin{aligned} |(I-U)x|=\frac{||b_i^{t+1}-b_i^t||}{r}\leqslant \frac{||b_i^{t+1}-b_i^t||}{d}, \end{aligned}$$

which shows that this term is Lipschitz as well, and specifically that

$$\begin{aligned} \left( \frac{\lambda ^c_{b_i^{t+1}}}{\lambda ^c_{b_i^t}}\right) ^2|I -P_{b_i^t\rightarrow b_i^{t+1}}|\,||\nabla _{b_i} {\mathcal {L}}(b_i^t)|| \leqslant C_4(C_5+C_6/d)||b_i^{t+1}-b_i^t||. \end{aligned}$$

Therefore, ${{\,\textrm{grad}\,}}_{b_i}{\mathcal {L}}$ is Lipschitz on K in the Riemannian sense, with the coefficient $C_1(C_2+C_3+C_4(C_5+C_6/d))$.

For the weights, ${{\,\textrm{grad}\,}}_{W_i}{\mathcal {L}} =\nabla _{W_i}{\mathcal {L}}$ since the weights are Euclidean. By the same considerations as above, the loss function is $C^2$ with respect to W as well, so we immediately obtain that ${{\,\textrm{grad}\,}}_W{\mathcal {L}}$ is locally Lipschitz since its Hessian is continuous, and thus bounded on compact sets.

Fig. 1

The transported vector is rotated by angle $\theta$

4 Experiments

We evaluate these methods on two benchmarks: the realizable case where the ground-truth output is given by another network, the MNIST dataset, and the WordNet dataset [7]. Note that, although we required a dynamic choice of step size above, our results here all use a constant step size, which suggests that a dynamic step size is not fundamentally required.

4.1 Realizable Case

We train by RSGD a model f with hidden hyperbolic layers and a Euclidean output layer, with labels $y_i$ generated by a ground-truth network $y_i=f({\textbf {W}}^*,x_i)$ of the same architecture. The dataset is $x_i\sim \exp ^c_0({\mathcal {N}}(0,I))$. (This is the pseudohyperbolic Gaussian [8].)

Our results for networks with various depth and width are shown in Fig. 2. We can see that training does appear to converge regardless of depth.

Fig. 2

Training by RSGD in the realizable case

Although losses appear to decrease smoothly over epochs, by inspecting samples within an epoch, the stochasticity can be observed (Fig. 3).

Fig. 3

Loss after each sample in one epoch of training

4.2 WordNet

WordNet is a large database of English noun synsets (collections of synonyms), together with hyponymy relations (“is-a” relationships). This means that the WordNet dataset has the hierarchical structure of a directed tree, which is the type of problem on which we expect hyperbolic networks to perform well in practice. We first generate a hyperbolic embedding of the transitive closure of the WordNet mammal subtree into ${\mathbb {D}}^2$, as in [10].

We then train a classifier with 2 hyperbolic hidden layers of width 32 to determine whether a given point in the embedding represents an aquatic mammal (i.e., is a child node of the aquatic_mammal synset), using each of the training algorithms discussed in this paper. Results are shown in Fig. 4. As expected, we see that each algorithm does converge, with RAdam converging much faster and achieving much better results before plateauing.

Fig. 4

Training by RGD, RSGD, and RAdam on WordNet mammals

5 Conclusion

We showed that HFFNNs are guaranteed to converge under training by RSGD, given some natural conditions, regardless of the choice of curvature or the number or size of layers. Experimentally, we use our own implementation to show that the convergence rate is reasonable. Furthermore, we implement RAdam and show that it provides substantial speedup in practice.