Skip to main content
SpringerLink
Log in

Two-Dimensional Riemann Problems: Transonic Shock Waves and Free Boundary Problems

  • Review Article
  • Published:
Communications on Applied Mathematics and Computation Aims and scope Submit manuscript

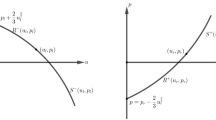
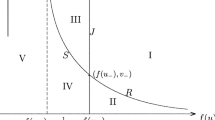
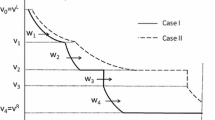
Abstract

We are concerned with global solutions of multidimensional (M-D) Riemann problems for nonlinear hyperbolic systems of conservation laws, focusing on their global configurations and structures. We present some recent developments in the rigorous analysis of two-dimensional (2-D) Riemann problems involving transonic shock waves through several prototypes of hyperbolic systems of conservation laws and discuss some further M-D Riemann problems and related problems for nonlinear partial differential equations. In particular, we present four different 2-D Riemann problems through these prototypes of hyperbolic systems and show how these Riemann problems can be reformulated/solved as free boundary problems with transonic shock waves as free boundaries for the corresponding nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear partial differential equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Agarwal, R., Halt, D.: A modified CUSP scheme in wave/particle split form for unstructured grid Euler flows. In: Caughey, D.A., Hafez, M.M. (eds.) Frontiers of Computational Fluid Dynamics, 155–163. World Scientific, Singapore (1994)

  2. Bae, M., Chen, G.-Q., Feldman, M.: Regularity of solutions to regular shock reflection for potential flow. Invent. Math. 175(3), 505–543 (2009)

    MathSciNet  MATH  Google Scholar 

  3. Bae, M., Chen, G.-Q., Feldman, M.: Prandtl-Meyer Reflection Configurations, Transonic Shocks, and Free Boundary Problems, Research Monograph, 233 pages. Memoirs of the American Mathematical Society, Providence, RI (2023)

    Google Scholar 

  4. Bargman, V.: On nearly glancing reflection of shocks. Office Sci. Res. and Develop. Rep. No. 5117 (1945)

  5. Ben-Dor, G.: Shock Wave Reflection Phenomena. Springer, New York (1991)

    MATH  Google Scholar 

  6. Bressan, A., Chen, G.-Q., Lewicka, M., Wang, D.-H.: Nonlinear Conservation Laws and Applications. The IMA Volumes in Mathematics and Its Applications, vol. 153, Springer, New York (2011)

  7. Canic, S., Keyfitz, B.L., Kim, E.H.: Free boundary problems for nonlinear wave systems: Mach stems for interacting shocks. SIAM J. Math. Anal. 37(6), 1947–1977 (2006)

    MathSciNet  MATH  Google Scholar 

  8. Chang, T., Chen, G.-Q.: Diffraction of planar shock along the compressive corner. Acta Math. Sci. 6, 241–257 (1986)

    MATH  Google Scholar 

  9. Chang, T., Chen, G.-Q., Yang, S.: \(2\)-D Riemann problem in gas dynamics and formation of spiral. In: Nonlinear Problems in Engineering and Science—Numerical and Analytical Approach (Beijing, 1991), pp. 167–179, Science Press, Beijing (1992)

  10. Chang, T., Chen, G.-Q., Yang, S.: On the 2-D Riemann problem for the compressible Euler equations. I. Interaction of shocks and rarefaction waves. Discrete Contin. Dynam. Syst. 1, 555–584 (1995)

    MathSciNet  MATH  Google Scholar 

  11. Chang, T., Chen, G.-Q., Yang, S.: On the 2-D Riemann problem for the compressible Euler equations. II. Interaction of contact discontinuities. Discrete Contin. Dynam. Syst. 6, 419–430 (2000)

    MATH  Google Scholar 

  12. Chang, T., Hsiao, L.: The Riemann problem and interaction of waves in gas dynamics. Longman Scientific & Technical, Harlow; John Wiley & Sons, Inc, New York (1989)

  13. Chen, G.-Q.: Euler equations and related hyperbolic conservation laws. Chapter 1. In: Dafermos, C.M., Feireisl, E. (eds.) Handbook of Differential Equations, Evolutionary Equations, Vol. 2, Elsevier, Amsterdam (2005)

  14. Chen, G.-Q.: Supersonic flow onto solid wedges, multidimensional shock waves and free boundary problems. Sci. Chin. Math. 60(8), 1353–1370 (2017)

    MathSciNet  MATH  Google Scholar 

  15. Chen, G.-Q., Chen, J., Xiang, W.: Stability of attached transonic shocks in steady potential flow past three-dimensional wedges. Commun. Math. Phys. 387, 111–138 (2021)

    MathSciNet  MATH  Google Scholar 

  16. Chen, G.-Q., Cliffe, A., Huang, F., Liu, S., Wang, Q.: On the Riemann problem with four-shock interaction for the Euler equations for potential flow, Preprint (2022)

  17. Chen, G.-Q., Deng, X., Xiang, W.: Shock diffraction by convex cornered wedges for the nonlinear wave system. Arch. Ration. Mech. Anal. 211, 61–112 (2014)

    MathSciNet  MATH  Google Scholar 

  18. Chen, G.-Q., Fang, B.-X.: Stability of transonic shock-fronts in steady potential flow past a perturbed cone. Discrete Contin. Dyn. Syst. 23, 85–114 (2009)

    MathSciNet  MATH  Google Scholar 

  19. Chen, G.-Q., Fang, B.-X.: Stability of transonic shocks in steady supersonic flow past multidimensional wedges. Adv. Math. 314, 493–539 (2017)

    MathSciNet  MATH  Google Scholar 

  20. Chen, G.-Q., Feldman, M.: Multidimensional transonic shocks and free boundary problems for nonlinear equations of mixed type. J. Am. Math. Soc. 16, 461–494 (2003)

    MathSciNet  MATH  Google Scholar 

  21. Chen, G.-Q., Feldman, M.: Global solutions to shock reflection by large-angle wedges for potential flow. Ann. Math. 171, 1019–1134 (2010)

    MathSciNet  Google Scholar 

  22. Chen, G.-Q., Feldman, M.: Mathematics of Shock Reflection-Diffraction and von Neumann’s Conjecture. Research Monograph, Annals of Mathematics Studies, 197. Princeton University Press, Princetion (2018)

    Google Scholar 

  23. Chen, G.-Q., Feldman, M.: Multidimensional transonic shock waves and free boundary problems. Bull. Math. Sci. 12(1), Paper No. 2230002 (2022)

  24. Chen, G.-Q., Feldman, M., Hu, J., Xiang, W.: Loss of regularity of solutions of the shock diffraction problem by a convex cornered wedge for the potential flow equation. SIAM J. Math. 52(2), 1096–1114 (2020)

    MathSciNet  MATH  Google Scholar 

  25. Chen, G.-Q., Feldman, M., Xiang, W.: Convexity of self-similar transonic shock waves for potential flow. Arch. Ration. Mech. Anal. 238, 47–124 (2020)

    MathSciNet  MATH  Google Scholar 

  26. Chen, G.-Q., Feldman, M., Xiang, W.: Uniqueness of regular shock reflection/diffraction configurations for potential flow, Preprint (2022)

  27. Chen, G.-Q., Kuang, J., Zhang, Y.: Stability of conical shocks in the three-dimensional steady supersonic isothermal flows past Lipschitz perturbed cones. SIAM J. Math. Anal. 53, 2811–2862 (2021)

    MathSciNet  MATH  Google Scholar 

  28. Chen, G.-Q., LeFloch, P.: Entropy flux-splittings for hyperbolic conservation laws. Comm. Pure Appl. Math. 48, 691–729 (1995)

    MathSciNet  MATH  Google Scholar 

  29. Chen, G.-Q., Li, D., Tan, D.-C.: Structure of the Riemann solutions for two-dimensional scalar conservation laws. J. Differ. Equ. 127(1), 124–147 (1996)

    MATH  Google Scholar 

  30. Chen, G.-Q., Shahgholian, H., Vázquez, J.-V.: Free boundary problems: the forefront of current and future developments. In: Free Boundary Problems and Related Topics. Theme Volume: Phil. Trans. R. Soc. A. 373, 20140285. The Royal Society, London (2015)

  31. Chen, G.-Q., Wang, Q., Zhu, S.-G.: Global solutions of a two-dimensional Riemann problem for the pressure gradient system. Comm. Pure Appl. Anal. 20, 2475–2503 (2021)

    MathSciNet  MATH  Google Scholar 

  32. Chen, S.-X.: Mathematical Analysis of Shock Wave Reflection. Series in Contemporary Mathematics 4, Shanghai Scientific and Technical Publishers, China; Springer Nature Singapore Pte Ltd., Singapore (2020)

  33. Chiodaroli, E., De Lellis, C., Kreml, O.: Global ill-posedness of the isentropic system of gas dynamics. Comm. Pure Appl. Math. 68, 1157–1190 (2015)

    MathSciNet  MATH  Google Scholar 

  34. Courant, R., Friedrichs, K.O.: Supersonic Flow and Shock Waves. Springer, New York (1948)

    MATH  Google Scholar 

  35. Dafermos, C.M.: Hyperbolic Conservation Laws in Continuum Physics. 4th edn. Springer, Berlin (2016)

    MATH  Google Scholar 

  36. Elling, V.: Non-existence of strong regular reflections in self-similar potential flow. J. Differ. Eqs. 252, 2085–2103 (2012)

    MathSciNet  MATH  Google Scholar 

  37. Elling, V., Liu, T.-P.: Supersonic flow onto a solid wedge. Comm. Pure Appl. Math. 61, 1347–1448 (2008)

    MathSciNet  MATH  Google Scholar 

  38. Fletcher, C.H., Taub, A.H., Bleakney, W.: The Mach reflection of shock waves at nearly glancing incidence. Rev. Modern Phys. 23(3), 271–286 (1951)

    MathSciNet  MATH  Google Scholar 

  39. Fletcher, C.H., Weimer, D.K., Bleakney, W.: Pressure behind a shock wave diffracted through a small angle. Phys. Rev. 78(5), 634–635 (1950)

    Google Scholar 

  40. Friedman, A.: Variational Principles and Free-Boundary Problems. 2nd edn. Robert E. Krieger Publishing Co., Inc., Malabar, Florida, (1988) [First edition, John Wiley & Sons, Inc., New York, 1982]

  41. Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order.  2nd edn. Springer-Verlag, Berlin (1983)

    MATH  Google Scholar 

  42. Glimm, J.: Solutions in the large for nonlinear hyperbolic systems of equations. Comm. Pure Appl. Anal. 18, 697–715 (1965)

    MathSciNet  MATH  Google Scholar 

  43. Glimm, J., Klingenberg, C., McBryan, O., Plohr, B., Sharp, D., Yaniv, S.: Front tracking and two-dimensional Riemann problems. Adv. Appl. Math. 6, 259–290 (1985)

    MathSciNet  MATH  Google Scholar 

  44. Glimm, J., Majda, A.: Multidimensional Hyperbolic Problems and Computations. The IMA Volumes in Mathematics and Its Applications, vol. 29. Springer, New York (1991)

    MATH  Google Scholar 

  45. Guckenheimer, J.: Shocks and rarefactions in two space dimensions. Arch. Ration. Mech. Anal. 59, 281–291 (1975)

    MathSciNet  MATH  Google Scholar 

  46. Guderley, K.G.: The Theory of Transonic Flow. Translated from German by Moszynski, J.R. Pergamon Press, New York (1962)

  47. Harabetian, E.: Diffraction of a weak shock by a wedge. Comm. Pure Appl. Math. 40, 849–863 (1987)

    MathSciNet  MATH  Google Scholar 

  48. Hunter, J.K., Keller, J.B.: Weak shock diffraction. Wave Motion 6, 79–89 (1984)

    MathSciNet  MATH  Google Scholar 

  49. Keller, J.B., Blank, A.A.: Diffraction and reflection of pulses by wedges and corners. Comm. Pure Appl. Math. 4, 75–94 (1951)

    MathSciNet  MATH  Google Scholar 

  50. Kim, E.H.: A global sub-sonic solution to an interacting transonic shock of the self-similar nonlinear wave equation. J. Differ. Equ. 248, 2906–2930 (2010)

    MATH  Google Scholar 

  51. Klingenberg, C., Kreml, O., Mácha, V., Markfelder, S.: Shocks make the Riemann problem for the full Euler system in multiple space dimensions ill-posed. Nonlinearity 33, 6517–6540 (2020)

    MathSciNet  MATH  Google Scholar 

  52. Kurganov, A., Tadmor, E.: Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers. Numer. Methods Partial Differ. Eqs. 18, 584–608 (2002)

    MathSciNet  MATH  Google Scholar 

  53. Lai, G., Sheng, W.: Two-dimensional pseudosteady flows around a sharp corner. Arch. Ration. Mech. Anal. 241, 805–884. (2021)

    MathSciNet  MATH  Google Scholar 

  54. Lax, P. D.: Shock waves and entropy. In: Zarantonllo, E.A. (ed.) Contributions to Nonlinear Functional Analysis, pp. 603–634. Academic Press, New York (1971)

  55. Lax, P.D.: Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves, CBMS-RCSM. SIAM, Philiadelphia (1973)

    Google Scholar 

  56. Lax, P.D., Liu, X.-D.: Solution of two-dimensional Riemann problems of gas dynamics by positive schemes. SIAM J. Sci. Comput. 19, 319–340 (1998)

    MathSciNet  MATH  Google Scholar 

  57. LeVeque, R.J.: Numerical Methods for Conservation Laws. Birkhäuser, Basel (1992)

    MATH  Google Scholar 

  58. Li, J., Yang, Z., Zheng, Y.: Characteristic decompositions and interactions of rarefaction waves of 2-D Euler equations. J. Differ. Equ. 250, 782–798 (2011)

    MathSciNet  MATH  Google Scholar 

  59. Li, J., Zhang, T., Yang, S.: The Two-Dimensional Riemann Problem in Gas Dynamics. Longman Scientific & Technical, Harlow (1998)

    MATH  Google Scholar 

  60. Li, J., Zheng, Y.: Interaction of rarefaction waves of the two-dimensional self-similar Euler equations. Arch. Ration. Mech. Anal. 193, 623–657 (2009)

    MathSciNet  MATH  Google Scholar 

  61. Li, J., Zheng, Y.: Interaction of four rarefaction waves in the bi-symmetric class of the two-dimensional Euler equations. Commun. Math. Phys. 296, 303–321 (2010)

    MathSciNet  MATH  Google Scholar 

  62. Li, Y.F., Cao, Y.M.: Large-particle difference method with second-order accuracy in gas dynamics. Sci. Chin. 28A, 1024–1035 (1985)

    MATH  Google Scholar 

  63. Lighthill, M.J.: The diffraction of a blast I. Proc. R. Soc. Lond. 198A, 454–470 (1949)

    MathSciNet  MATH  Google Scholar 

  64. Lighthill, M.J.: The diffraction of a blast II. Proc. R. Soc. Lond. 200A, 554–565 (1950)

    MathSciNet  Google Scholar 

  65. Lindquist, W.B.: Scalar Riemann problem in two spatial dimensions: piecewise smoothness of solutions and its breakdown. SIAM J. Math. Anal. 17, 1178–1197 (1986)

    MathSciNet  MATH  Google Scholar 

  66. Liu, T.-P.: Admissible Solutions of Hyperbolic Conservation Laws. Memoirs of the American Mathematical Society, 30(240), 1–78 (1981)

  67. Lock, G.D., Dewey, J.M.: An experimental investigation of the sonic criterion for transition from regular to Mach reflection of weak shock waves. Exp. Fluids 7, 289–292 (1989)

    Google Scholar 

  68. Mach, E.: Über den verlauf von funkenwellenin der ebene und im raume. Sitzungsber. Akad. Wiss. Wien 78, 819–838 (1878)

    Google Scholar 

  69. Majda, A.: Compressible Fluid Flow and Systems of Conservation Laws in Several Space Variables. Springer, New York (1984)

    MATH  Google Scholar 

  70. Menikoff, R., Plohr, B.: Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 61, 75–130 (1989)

    MathSciNet  MATH  Google Scholar 

  71. Meyer, Th.: Über zweidimensionale Bewegungsvorgänge in einem Gas, das mit Überschallgeschwindigkeit strömt. Dissertation, Göttingen, 1908. Forschungsheft des Vereins deutscher Ingenieure, vol. 62, pp. 31–67, Berlin (1908)

  72. Morawetz, C.S.: Potential theory for regular and Mach reflection of a shock at a wedge. Comm. Pure Appl. Math. 47, 593–624 (1994)

    MathSciNet  MATH  Google Scholar 

  73. Prandtl, L.: Allgemeine Überlegungen über die Strömung zusammendrückbarer Fluüssigkeiten. Z. Angew. Math. Mech. 16, 129–142 (1938)

    MATH  Google Scholar 

  74. Riemann, B.: Über die Fortpflanzung ebener Luftvellen von endlicher Schwingungsweite. Gött. Abh. Math. Cl. 8, 43–65 (1860)

    Google Scholar 

  75. Schulz-Rinne, C.W.: Classification of the Riemann problem for two-dimensional gas dynamics. SIAM J. Math. Anal. 24, 76–88 (1993)

    MathSciNet  MATH  Google Scholar 

  76. Schulz-Rinne, C.W., Collins, J.P., Glaz, H.M.: Numerical solution of the Riemann problem for two-dimensional gas dynamics. SIAM J. Sci. Comput. 14, 1394–1414 (1993)

    MathSciNet  MATH  Google Scholar 

  77. Serre, D.: Shock reflection in gas dynamics. In: Handbook of Mathematical Fluid Dynamics, vol. 4, pp. 39–122. Elsevier, North-Holland (2007)

  78. Shu, C.-W.: Essentially non-oscillatory and weighted essentially non-oscillatory schemes. Acta Numer. 29, 701–762 (2020)

    MathSciNet  MATH  Google Scholar 

  79. Smoller, J.: Shock Waves and Reaction-Diffusion Equations. Springer, New York (1982)

    MATH  Google Scholar 

  80. Tan, D.C., Zhang, T.: Two-dimensional Riemann problem for a hyperbolic system of nonlinear conservation laws (I)–(II). J. Differ. Equ. 111, 203–282 (1994)

    MATH  Google Scholar 

  81. Van Dyke, M.: An Album of Fluid Motion. The Parabolic Press, Stanford (1982)

    Google Scholar 

  82. Von Neumann, J.: Theory of shock waves, Progress Report. U.S. Dept. Comm. Off. Tech. Serv. No. PB32719, Washington, DC (1943)

  83. Von Neumann, J.: Oblique reflection of shocks, Explo. Res. Rep. 12. Navy Department, Bureau of Ordnance, Washington, DC (1943)

  84. Von Neumann, J.: Refraction, intersection, and reflection of shock waves, NAVORD Rep. 203-45. Navy Department, Bureau of Ordnance, Washington, DC (1945)

  85. Von Neumann, J.: Collected Works, vol. 6. Pergamon, New York (1963)

    MATH  Google Scholar 

  86. Von Neumann, J.: Discussion on the existence and uniqueness or multiplicity of solutions of the aerodynamical equation [Reprinted from MR0044302 (1949)]. Bull. Amer. Math. Soc. (N.S.), 47, 145–154 (2010)

  87. Wagner, D.H.: The Riemann problem in two space dimensions for a single conservation laws. SIAM J. Math. Anal. 14, 534–559 (1983)

    MathSciNet  MATH  Google Scholar 

  88. Wendroff, B.: The Riemann problem for materials with nonconvex equations of state: I. Isentropic flow. J. Math. Anal. Appl. 38, 454–466 (1972)

  89. Wendroff, B.: The Riemann problem for materials with nonconvex equations of state: II. General flow. J. Math. Anal. Appl. 38, 640–658 (1972)

  90. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  91. Woodward, P., Colella, P.: The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comp. Phys. 54, 115–173 (1984)

    MathSciNet  MATH  Google Scholar 

  92. Zhang, P., Li, J., Zhang, T.: On two-dimensional Riemann problem for pressure-gradient equations of the Euler system. Discrete Contin. Dynam. Systems 4, 609–634 (1998)

    MathSciNet  MATH  Google Scholar 

  93. Zhang, T., Zheng, Y.: Two-dimensional Riemann problem for a scalar conservation law. Trans. Am. Math. Soc. 312, 589–619 (1989)

    MATH  Google Scholar 

  94. Zhang, T., Zheng, Y.: Conjecture on the structure of solutions of the Riemann problem for two-dimensional gas dynamics. SIAM J. Math. Anal. 21, 593–630 (1990)

    MathSciNet  MATH  Google Scholar 

  95. Zheng, Y.: Existence of solutions to the transonic pressure gradient equations of the compressible Euler equations in elliptic regions. Commun. Partial Differ. Equ. 22, 1849–1868 (1997)

    MathSciNet  MATH  Google Scholar 

  96. Zheng, Y.: A global solution to a two-dimensional Riemann problem involving shocks as free boundaries. Acta Math. Appl. Sin. 19(4), 559–572 (2003)

    MathSciNet  MATH  Google Scholar 

  97. Zheng, Y.: Two-dimensional regular shock reflection for the pressure gradient system of conservation laws. Acta Math. Appl. Sin. 22(2), 177–210 (2006)

    MathSciNet  MATH  Google Scholar 

  98. Zheng, Y.: Systems of Conservation Laws: Two-Dimensional Riemann Problems, vol. 38. Springer, New York (2012)

    Google Scholar 

Download references

Acknowledgements

This paper is dedicated to Professor Tong Zhang (Tung Chang) on the occasion of his 90th birthday, who has been one of the pioneers and main contributors in the analysis of the 2-D Riemann problems; see for example [8,9,10,11,12, 59, 80, 92,93,94] and the references cited therein. The research of Gui-Qiang G. Chen was supported in part by the UK Engineering and Physical Sciences Research Council Awards EP/L015811/1, EP/V008854/1, EP/V051121/1, and the Royal Society-Wolfson Research Merit Award WM090014.

Author information

Authors and Affiliations

  1. Oxford Centre for Nonlinear PDE, Mathematical Institute, University of Oxford, Oxford, OX2 6GG, UK

    Gui-Qiang G. Chen

Authors
  1. Gui-Qiang G. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Gui-Qiang G. Chen.

Ethics declarations

Conflict of Interest

There is no conflict of interest.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, GQ.G. Two-Dimensional Riemann Problems: Transonic Shock Waves and Free Boundary Problems. Commun. Appl. Math. Comput. 5, 1015–1052 (2023). https://doi.org/10.1007/s42967-022-00210-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42967-022-00210-4

Keywords

Mathematics Subject Classification

Search

Navigation