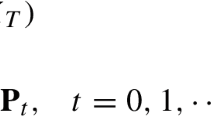Abstract
In contrast to traditional financial advising, robo-advising needs to elicit investors’ risk profile via several simple online questions and provide advice consistent with conventional investment wisdom, e.g., rich and young people should invest more in risky assets. To meet the two challenges, we propose to do the asset allocation part of robo-advising using a dynamic mean-variance criterion over the portfolio’s log returns. We obtain analytical and time-consistent optimal portfolio policies under jump-diffusion models and regime-switching models.




Similar content being viewed by others
Notes
Of course, for the last two rules to hold, one needs some reasonable assumptions.
Here we assume the square integrability of \(\hat{\pi }\) under some mild conditions on \(\mu (\cdot , \cdot ;\, i)\) and \(\sigma (\cdot ,\cdot ; \, i)\).
We assume that the investor using our system knows the meaning of the average and the standard deviation and understands the basic trade-off between risk and return; otherwise, it is perhaps better for the investor to seek advice from a professional financial advisor directly or to buy other financial products such as fixed annuity contracts, rather than using the robo-advising.
References
Ang, A., & Bekaert, G. (2002). International asset allocation with regime shifts. Review of Financial Studies, 15, 1137–1187.
Basak, S., & Chabakauri, G. (2010). Dynamic mean-variance asset allocation. Review of Financial Studies, 23, 2970–3016.
Björk, T., Khapko, M., & Murgoc, A. (2017). On time-inconsistent stochastic control in continuous time. Finance and Stochastics, 21(2), 331–360.
Björk, T., Murgoci, A., & Zhou, X. Y. (2014). Mean-variance portfolio optimization with state-dependent risk aversion. Mathematical Finance, 24, 1–24.
Capponi, A., Olafsson, S., & Zariphopoulou, T. (2019). Personalized robo-advising: Enhancing investment through client interaction. arXiv:1911.01391.
Cai, J., Chen, X., & Dai, M. (2017). Portfolio selection with capital gains tax, recursive utility, and regime switching. Management Science,64(5), 2308–2324.
Chacko, G., & Viceira, L. M. (2005). Dynamic consumption and portfolio choice with stochastic volatility in incomplete markets. Review of Financial Studies,18, 1369–402.
Dai, M., Jin, H. Q., Kou, S., & Xu, Y. H. (2020). A dynamic mean-variance analysis for log returns. Management Science. https://doi.org/10.1287/mnsc.2019.3493.
Campbell, J. Y., & Viceira, L. M. (1999). Consumption and portfolio decisions when expected returns are time varying. Quarterly Journal of Economics,114, 433–495.
Kim, T. S., & Omberg, E. (1996). Dynamic nonmyopic portfolio behavior. Review of Financial Studies,9, 141–161.
Liu, J., Longstaff, F. A., & Pan, J. (2003). Dynamic asset allocation with event risk. The Journal of Finance,58(1), 231–259.
Liu, J. (2001). Dynamic portfolio choice and risk aversion. Working Paper, UCLA, SSRN-id287095.
Markowitz, H. (1952). Portfolio selection. The Journal of Finance, 7, 77–91.
Merton, R. C. (1971). Optimum consumption and portfolio rules in a continuous-time model. Journal of Economic Theory,3, 373–413.
Strub, M. S., Li, D., & Cui, X. Y. (2019). An enhanced mean-variance framework for robo-advising applications. Available at SSRN: https://ssrn.com/abstract=3302111.
Wachter, J. A. (2002). Portfolio and consumption decisions under mean-reverting returns: An explicit solution for complete market. Journal of Financial and Quantitative Analysis, 37, 63–91.
Zhou, X. Y., & Yin, G. (2003). Markowitz’s mean-variance portfolio selection with regime switching: A continuous-time model. SIAM Journal on Control and Optimization, 42(4), 1466–1482.
Funding
Funded by National Natural Science Foundation of China 11671292, 11871050, and 12071333, Singapore Academic Research Fund R-703-000-032-112, R-146-000-306-114, and R-146-000-311-114.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Proofs for results in section 2
Proofs for results in section 2
Proofs of proposition 1.
The value function is defined as \(V\left( t,R_{t}\right) =\mathrm {E} _{t}(R_{T}^{*})-\frac{\gamma }{2}\mathrm {Var}_{t}(R_{T}^{*})\), where \(R^{*}\) is the log return with equilibrium \(\hat{\pi }\). Let \(g\left( t,R_{t}\right) :=\mathrm {E}_{t}\left[ R_{T}^{*}\right]\). By the structures of \(R_{T}^{*}\) and the conditional expectation and the conditional variance, we consider the forms
Furthermore, we have, via the general extended HJB in Björk et al. (2017), that
subject to \(V(T,R)=R\), where \(\mathcal {D}\) is the Dynkin operator. For a function F of \(\left( t,R\right)\), \(\mathcal {D}F\left( t,R\right) =\frac{\partial F}{\partial t}+\left( r+\left( \mu -r\right) \pi -\frac{1}{2}\sigma ^{2}\pi ^{2}\right) \frac{\partial F}{\partial R}+\frac{1}{2}\sigma ^{2}\pi ^{2}\frac{\partial ^{2} F}{\partial R^{2}}+\int _{\mathbb {R}}\left[ F\left( t,R_{t^{-}}+\ln \left( 1+\beta \pi \right) \right) -F\left( t,R_{t^{-}}\right) \right] \lambda \left( \mathrm{d}z\right)\). Incorporating the special forms (18) and (19), we have
We then obtain the equilibrium strategy (5) by the first-order condition. \(\square\)
Proof of Proposition 2.
For any proportional portfolio \(\pi\), by the dynamics of the log return process \(\{R(t;\pi )\}\), we have, given \(R(t,\pi )=R\), that
and the objective function is to maximize
Let \(\hat{\pi }(t, R, x, i)\) be an equilibrium feedback proportional allocation, \(\{R(s)\}\) be the resulted log return process, \(\{\hat{\pi }_s\}\) be the proportional portfolio process, and V(t, R, x, i) be the value function. Define
It is easy to see that \(J(t,R,X_t;\pi , \alpha (t))-R\) is not explicitly dependent on R, this gives us the conjecture that V(t, R, x, i) admits the form
By this form and the definition of equilibrium solution, we then obtain the PDE
subject to \(\tilde{V}(T,x,i)=0\), where we used the simplified notations \(\mu ^i:=\mu (t, x; i), \sigma ^i:=\sigma (t, x; i), m_i:=m( x; i), \nu _i=\nu (x;i)\), and
If \(\tilde{V}\) is a solution to this equation, then the optimal \(\pi ^*=\hat{\pi }(t,x;i)\) will be the equilibrium feedback strategy.
By the first-order condition, an equilibrium optimal trading strategy is as given in (7). Substituting \(\hat{\pi }\) into \(f^{i}\) gives
with some abusing of notations \(r_s=r(s,X_s;\alpha (s)), \mu _s=\mu (s, X_s;\alpha (s)), \sigma _s=\sigma (s,X_s;\alpha (s))\) and \(m_s=m(X_s;\alpha (s)), \nu _s=\nu (X_s;\alpha (s))\).
By the Feynman-Kac formula, we infer that \(f^{i}\) satisfies (8). \(\square\)
Proof of Corollary 1: For conciseness, we use \(f^i\) to mean the function \(f(\cdot , \cdot ; i)\). For the Gaussian mean returns model, the PDE (8) becomes
Consider a solution of the following quadratic form:
Substituting this into (21) and by separating variables, we obtain the following ODE system:
Hence, by Proposition 2, the equilibrium strategy is as given in (11). \(\square\)
Proof of Corollary 2: Note that in the stochastic volatility model, \(\mu (i)-r_{i}=\delta _{i} x^{\frac{1+\beta }{2\beta }},\ \sigma (i)=x^{\frac{1}{2\beta }},\ m_{i} =\lambda (i)\bar{X}(i)-\lambda (i)x\), and \(\nu (i)=\bar{\nu }(i)x^{\frac{1}{2}}\). Then PDE (8) becomes
We try a solution of the following linear form:
Substituting this into (22) and by separating variables, we obtain the following ODE system:
Hence, by Proposition 2, the equilibrium strategy is as given in (16). \(\square\)
Rights and permissions
About this article
Cite this article
Dai, M., Jin, H., Kou, S. et al. Robo-advising: a dynamic mean-variance approach. Digit Finance 3, 81–97 (2021). https://doi.org/10.1007/s42521-021-00028-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42521-021-00028-4