Bayesian Analysis of First-Order Markov Models for Autocorrelated Binary Responses

Abstract

In many clinical trials, patient outcomes are often binary-valued which are measured asynchronously over time across various dose levels. To account for autocorrelation among such longitudinally observed outcomes, a first-order Markov model for binary data is developed. Moreover, to account for the asynchronously observed time points, nonhomogeneous models for the transition probabilities are proposed. The transition probabilities are modeled using B-spline basis functions after suitable transformations. Additionally, if the underlying dose-response curve is assumed to be non-decreasing, our model allows for the estimation of any underlying non-decreasing curve based on suitably constructed prior distributions. We also extended our model to the mixed effect model to incorporate individual-specific random effects. Numerical comparisons with traditional models are provided based on simulated data sets, and also practical applications are illustrated using real data sets.

1 Introduction

In many clinical trials, patient outcomes are often binary-valued that are measured asynchronously over time across various dose levels. For example, for patients with toenail infection, a popular measure of clinical efficacy of treatment for the nail is a 4-point scale (cleared, minimal symptoms, slightly improved, failure). A significant improvement is defined as cleared or minimal clinical symptoms at the end of the study. Thus, the efficacy outcome is a binary random variable, with 1 indicating significant improvement and 0 otherwise. As these binary-valued responses measured over time for each patient are likely to be different for different patients and expected to be correlated over time, a first-order Markov model that allows capturing such autocorrelations is often used to analyze the data sets.

In most of the common modeling approaches, the Markov chain is often considered to be time-homogeneous. That is, the transition probability from one state to another (e.g., a value of 1 to 0 in the case of binary data) depends only on the difference between state values and is independent of the time index. For example, Shoko and Chikobvu [1] used the time-homogeneous Markov process to model HIV/AIDS progression using a cohort study. Similarly, Ma et al. [2] developed a Bayesian approach using the log transformation of $S \times S$ transition probability matrix, where S is the total number of observed outcomes of all subjects, assuming the time-homogeneous Markov process.

However, it is more natural in general to assume that the probability of state-to-state jumps may change as time goes on. For example, the probability of showing improvement would depend on how long the patient has been on treatment. However, modeling a nonhomogeneous Markov chain is relatively difficult as the common stationary property does not hold and the dimension of parameters to estimate is large. Previously, Jackson et al. [3] reviewed various Markov models and their extension to fit a continuous-time panel data, but this approach for the time nonhomogeneous model is restricted to piecewise-constant transition probabilities. Hubbard et al. [4] proposed the time nonhomogeneous models by transforming the time scale of the nonhomogeneous Markov process to the time scale of the homogeneous process. However, these models relied on the assumption that the ratio of transition probabilities stays constant over time. Jones et al. [5] modeled the nonhomogeneous transition probabilities of longitudinal binary data as exponential functions. Zeng and Cook [6] proposed an estimation and inference method for transition probability using Generalized Estimating Equation approaches and logistic regression. However, these models may be inconsistent if the true transition probability functions are different from their assumed models. B-spline basis functions can be used to model smooth curves. For example, Andersen et al. [7] modeled occupancy in an office environment using the nonhomogeneous Markov model where the transition probabilities are estimated using B-splines and exponential smoothing. Similarly, Iversen et al. [8] proposed a non-homogeneous Markov model using logit transformation and the B-spline basis to describe driving patterns of electric vehicles. However, these models lack solving the missingness, which is often the case in clinical outcome data.

The proposed model provides a Bayesian approach for the flexible non-homogeneous Markov model for autocorrelated binary responses. One major disadvantage of the common nonhomogeneous Markov model is that there are a large number of parameters to be estimated. In our model, B-spline basis functions are used to reduce the number and to estimate a smooth transition probability curve without any assumptions about the shape of the curve. Our proposed model, using a Bayesian framework, allows dealing with non-ignorable missingness and unbalance problems with ease based on suitably constructed prior distributions.

This paper is organized as follows: Sect. 2 introduces the proposed non-homogeneous Markov model for asynchronous data. In Sect. 3, numerical results are provided. Section 4 illustrates practical applications using toenail clinical trial data and Dow Jones stock market data. Section 5 concludes the paper with some discussion.

2 Non-homogeneous Markov Model for Asynchronous Data

2.1 Constructing Markov Properties

Suppose there are $i=1,....,n$ subjects and $Y_{i0}^{obs} = Y_i^{\textrm{obs}}(t_{i0})$ is the initial outcome of a subject i at initial time $t_0$. Also, suppose that each subject i has been measured at $J_i$ time points afterward. Let $t_{ij}$ be the jth time of subject i and $Y_{ij}^{\textrm{obs}} = Y_i^{\textrm{obs}}(t_{ij})$ be a binary outcome of the subject i at time $t_{ij}$, where $t_{i0}< t_{i1}< \cdots < t_{iJ_i}$. That is, for subject $i=1,...,n$ with $j=0,1,...,J_i$ observed time points,

$$\begin{aligned} Y_{ij}^{\textrm{obs}} = {\left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ the } \text{ subject } i \text{ had } \text{ an } \text{ event } \text{ at } \text{ time } t_{ij}\\ 0 &{} \text{ otherwise } \end{array}\right. }. \end{aligned}$$

Let $T_A = \sum _{i=1}^n J_i$ be the total number of observed time points of n subjects after initial time $t_0$, and let’s assume that among $T_A$ time points, there are T distinct time points where $\max _i(J_i) \le T \le T_A$. Also, let $\textbf{t}=(t_0, t_1,...,t_T)$ be the vector of all distinct ordered time points of length $T + 1$. In order to define the Markov property, we reconstruct the binary response outcome based on the all distinct time $\textbf{t}$. Specifically, for subjects i, the new outcome $Y_{ik}$, $k \in \textbf{t}$ is defined as $Y_{ik} = Y_{ij}^{\textrm{obs}}$ if $k = j$ for some $j = 1,...,J_i$, and missing if the subject i does not have an outcome at time k.

Figure 1 illustrates the construction of Markov properties on asynchronous data. Suppose that the first patient was observed four times and the corresponding outcome is $\textbf{y}_1 = (y_{11}^{\textrm{obs}},y_{12}^{\textrm{obs}},y_{13}^{\textrm{obs}},y_{14}^{\textrm{obs}})^{\textrm{T}}$. Similarly, the second patient has three outcomes and the third patient has 4 outcomes. The outcomes under the same vertical dashed line imply those were obtained at the same time. Since there are six distinct time points, we reconstruct the new response variable Y as,

$$\begin{aligned} Y = \begin{pmatrix} \textbf{y}_{1}\\ \textbf{y}_{2}\\ \textbf{y}_{3} \end{pmatrix} = \begin{pmatrix} y_{11}^{\textrm{obs}} &{} y_{12}^{\textrm{obs}} &{}. &{} y_{13}^{\textrm{obs}} &{}. &{} y_{14}^{\textrm{obs}}\\ y_{21}^{\textrm{obs}} &{} y_{22}^{\textrm{obs}} &{}. &{}. &{} y_{23}^{\textrm{obs}} &{}.\\ y_{31}^{\textrm{obs}} &{}. &{} y_{32}^{\textrm{obs}} &{}. &{} y_{33}^{\textrm{obs}} &{} y_{34}^{\textrm{obs}}\\ \end{pmatrix} = \begin{pmatrix} y_{11} &{} y_{12} &{}. &{} y_{14} &{}. &{} y_{16}\\ y_{21} &{} y_{22} &{}. &{}. &{} y_{25} &{}.\\ y_{31} &{}. &{} y_{33} &{}. &{} y_{35} &{} y_{36}\\ \end{pmatrix}. \end{aligned}$$

Fig. 1

Illustration of Markov chain construction. See the text for further details

When time points are different for every patient but close, we can reconstruct the outcome vector by applying a common practice in clinical trial studies that specifies an appropriate range of time, or visit window, to allow feasible scheduling of visit. For example, a week 4 visit can be defined as 4 weeks post study enrollment ± 1 week, and similarly for the week 8 and week 12 visits. In this way, such time points that are different but close can be grouped into a few pre-specified visits. In general, a similar time windowing strategy is applicable based on the research interest and subject matter knowledge.

For the reconstructed the outcome vector $Y_i = \{Y_{i0}, Y_{i1},...,Y_{iT} \}^{\textrm{T}}$, we assume that $Y_{i0}, Y_{i1},...,Y_{iT}$ has Markov properties. By the definition of the first-order Markov chain that the event at the current time only depends on the event at an immediate past time, two transition probability functions are defined as,

$$\begin{aligned} p(Y_{ij} = 1 \mid Y_{i,j-1}=1)&= \theta _{i1}(t_j) \\ p(Y_{ij} = 1 \mid Y_{i,j-1}=0)&= \theta _{i0}(t_j), \end{aligned}$$

for $j=1,...,T$. The initial probability is $\theta _{i,00} = p(Y_{i0}=1)$. In general, the transition probabilities may depend on individual i, but for simplicity, we begin with the setting that $\theta _{il}(t_j) = \theta _{l}(t_j)$ for $l = 0, 1$ and $j= 1,...,T$. By assuming that each individual is independent of each other, the corresponding generic model for a subject can be expressed by the following hierarchical model,

$$\begin{aligned} Y_0&\sim Ber(\theta _{00}) \\ Y_1 \mid Y_0&\sim Ber\left( \theta _1(t_1)Y_0 + \theta _0(t_1)(1-Y_0)\right) \\ Y_2 \mid Y_1&\sim Ber\left( \theta _1(t_2)Y_1 + \theta _0(t_2)(1-Y_1)\right) \\&\vdots \\ Y_{T} \mid Y_{{T}-1}&\sim Ber\left( \theta _{1}(t_{T})Y_{{T}-1} + \theta _{0}(t_{T})(1-Y_{{T}-1})\right) . \end{aligned}$$

In some applications such as dose-response model, it is natural to assume that the true transition probability function $\theta _l(t), ~l=0,1$ satisfies the non-decreasing condition: $\theta _l(t_0) \le \theta _l(t_1) \le \cdots$ for $t_0 \le t_1 \le t_2 \le \cdots$. Note that this condition is not necessary for our model development and can be relaxed or modified depending on the background information that we may have from the data.

2.2 Modeling Transition Probabilities with B-splines

As the observed data over time can be asynchronous, we would like to estimate the transition probabilities as smooth functions for any time $t \in [t_0,t_T]$. It is well known (see [9]) that if the underlying true transition probability $\theta _l(t)$ is smooth, then it can be uniformly approximated by a sequence of B-splines by choosing the appropriately large number of knots. In practice, the selection of the knots and number of knots are based on observed time points and the sample sizes making it data adaptive.

Let $\varvec{\kappa }$ be the vector of non-decreasing knots that $\kappa _0 = \min (\textbf{t}) \le \kappa _1 \le ... \le \kappa _{m} = \max (\textbf{t})$. The k-th B-spline basis functions of degree q with m internal knots at time t, written as $B_{k,q}(t)$, are recursive functions that are constructed as

$$\begin{aligned} B_{k,0}(t)&= {\left\{ \begin{array}{ll}1, &{} t \in [\kappa _{k},\kappa _{k+1}) \\ 0, &{} \text{ otherwise } \end{array}\right. }\\ B_{k,q}(t)&= \frac{t - \kappa _k}{\kappa _{k+q} - \kappa _k}B_{k,q-1}(t) + \frac{\kappa _{k+q+1}-t}{\kappa _{k+q+1}-\kappa _{k+1}}B_{k+1,q-1}(t), \text{ when } q \ge 1, \end{aligned}$$

where $k = 0,..., M = m + q$ and $\varvec{\kappa } = (\kappa _0,...,\kappa _M)$ is a vector of knots such that $\kappa _0 \le \kappa _1 \le ... \le \kappa _{M}$. The first knot $\kappa _0$ and the last knot $\kappa _M$ are boundary knots, and the first B-spline term $B_{0,q}$ is often regarded as the intercept. Using B-spline approximation, the transition probability function $\theta _l(t)$ can be estimated as a linear combination of a B-spline basis given by

$${\theta }_l(t)= \sum _{k=0}^{M}\beta _{lk}B_{k,q}(t) = \textbf{B}_M(t)^T\varvec{\beta }_l, ~ t \in [\kappa _0, \kappa _m],$$

where $\textbf{B}_M(t) = \{B_{0,q}(t),...,B_{M,q}(t) \} ^ {\textrm{T}}$ and $\varvec{\beta }_l = \{\beta _{l0},...,\beta _{lM} \}^{\textrm{T}}.$

For a fixed number of internal knots m and a spline degree q, B-spline basis functions form a partition of unity, i.e.,

$$\begin{aligned} \sum _{k=0}^{M} B_{k,q}(t) = 1, \text{ for } \text{ all } t, q. \end{aligned}$$

Therefore, if the coefficients $\beta _{lk}$s are restricted to be in the interval [0, 1] then ${\theta }_l(t) \in [0,1]$ for any $m \ge 1$ and $q \ge 1$. Typically, cubic spline with $q=3$ is used for the most practical applications.

Using the partition of unity property, the proposed model with the B-spline approximation is as follows,

$$\begin{aligned} Y_{i0}&\sim \text {Ber}(\theta _{00}) \text { where } \theta _{00} \sim \text {Beta}(1,1) \nonumber \\ Y_{ij} \mid Y_{i,j-1}&\sim \text {Ber}\left( \theta _{1}(t_j)Y_{i,j-1} + \theta _{0}(t_j)(1-Y_{i,j-1})\right) , ~~ j=1,...,T \nonumber \\ \theta _l(t_j)&= \sum _{k=1}^{M}\beta _{lk}B_{k,q}(t_j), ~~l=0,1 \nonumber \\ \beta _{lk}&\overset{\text {ind}}{\sim } \text {Beta}(\mu _k \tau ,(1-\mu _k)\tau ), ~ \forall l,k \nonumber \\ {}&\mu _k \overset{\text {ind}}{\sim } \text {Beta}(1,1) \nonumber \\ {}&\tau \sim \text {Unif}(0.1,10). \end{aligned}$$

(1)

The coefficients $\beta _{lk}$s were given a Beta prior to ensure that the transition probability function $\theta _l(t) \in [0,1]$ for $l = 0,1$ and for all t. The hyper-parameters $\mu _k$s, $k = 1,..,M$ represent the mean of the prior distribution of $\beta _{lk}$, and $\tau$ controls the variance of the distribution.

Alternatively, the logit transformation for $\varvec{\theta }_l$ can be used considering $\beta _{lk}$s as logistic regression coefficients. The primary advantage of using the logit transformation is that we no longer need any restriction on the coefficients $\beta _{lk}$s. This can be modeled as

$$\begin{aligned} Y_{i0}&\sim \text {Ber}(\theta _{00}) \text { where } \theta _{00} \sim \text {Beta}(1,1) \nonumber \\ Y_{it} \mid Y_{i,j-1}&\sim \text {Ber}\left( \theta _{1}(t_j)Y_{i,j-1} + \theta _{0}(t_j)(1-Y_{i,j-1})\right) , ~~ j=1,...,T \nonumber \\ \theta _l(t_j)&= \left[ 1 + \exp \left\{ - \sum _{k=1}^{M}\beta _{lk}B_{k,q}(t_j) \right\} \right] ^{-1}, ~~l=0,1 \nonumber \\ \beta _{lk}&\overset{\text {ind}}{\sim } N(\mu _k,\tau ) ~\forall k,l \nonumber \\ {}&\mu _k \overset{\text {iid}}{\sim } N(0,10^3) \nonumber \\ {}&\tau \sim IG(2,1). \end{aligned}$$

(2)

We refer to (1) as linear link model and (2) as logit link model. Our simulation studies in Sect. 3 show that the performance of both models is similar. Analogous to the linear link model, the hyper-parameters $\mu _k$s and $\tau$ represent the mean and variance of the prior distribution of $\beta _{lk}$s, respectively. However, as $\beta _{lk}$s are not restricted to the interval [0, 1], we give Gaussian prior to $\mu _k$s and the conjugate Inverse Gamma prior to $\tau$, i.e.,

$$\begin{aligned} \tau \mid \alpha ,\beta \sim IG(\alpha ,\beta ), ~~ p(\tau \mid \alpha , \beta ) = \frac{\beta ^{\alpha }}{\Gamma (\alpha )}\tau ^{-\alpha -1}\exp (-\beta /\tau ). \end{aligned}$$

Both models in (1) and (2) allow flexible estimation of the transition probability functions $\theta _l(t)$ for $l = 0, 1$ for autocorrelated and asynchronous binary outcomes.

In addition, one can consider probit link model by representing the transition probability functions as

$$\begin{aligned} \theta _l(t) = \Phi \left\{ \sum _{k=1}^{M}\beta _{lk}B_{k,q}(t) \right\} , ~~l=0,1, \end{aligned}$$

where $\Phi (\cdot )$ is a Gaussian CDF function. However, as we are using a nonparametric model, the results will not be sensitive with the choice of the link function because the function space spanned by either the use of logit or probit or any other CDF will be the same.

2.3 Non-decreasing Constraints

In many cases, the true transition probability curves are assumed to be non-decreasing functions. For example, the probability of transitioning from a severe symptom to a mild symptom would likely to be non-decreasing with respect to the time a patient was on a treatment. In such cases, our model allows for the estimation of the underlying non-decreasing curve. Meyer [10] proved that the non-decreasing constraint on $\beta _{lk}$ imposes the non-decreasing shape constraints on $\theta _l(t)$.

The linear link model (1) can easily be extended to incorporate non-decreasing constraints using the reparametrization technique following Shin and Ghosh [11] and Cutis and Ghosh [12]. Even though their method was applied to Bernstein polynomials [13], a similar technique can be applied to the B-spline basis functions. We consider the difference of the two consecutive coefficients, $\gamma _{lk} = \beta _{lk} - \beta _{l, k-1}$ and the partial sum of B-spline functions, $F_{k,q}(t) = \sum _{k=l}^MB_{k,q}(t)$ for $t \in [t_{k-1}, t_k] \text{ and } M = m + q + 1$. Then, we can represent the transition probability function $\theta _l(t)$ with non-decreasing constraints in terms of $\gamma _{lk}$ and $F_{kq}(t)$ as follows,

$$\begin{aligned} \theta _l(t)&= \textbf{B}_M(t)^T\varvec{\beta }_l= \textbf{F}_M(t)^T\varvec{\gamma }_l \text{ for } l=0,1 \nonumber \\&\text{ s.t. } ~ \begin{pmatrix} \textbf{I}_M \\ -\textbf{1}^T_M \end{pmatrix}{\varvec{\gamma }}_l \ge \begin{pmatrix} \textbf{0}_M \\ -1 \end{pmatrix}, \end{aligned}$$

(3)

where $\textbf{F}_M(t) = \{F_{0,q}(t),...,F_{M,q}(t) \} ^ T$ and $\varvec{\gamma }_l = \{\gamma _{l0},...,\gamma _{lM} \}^{\textrm{T}}$. The constraints in (3) imply $\gamma _{lk} \ge 0$ and $\sum _{k=1}^M\gamma _{lk} = \beta _{lM} \le 1$ for all $l = 0,1$ and $k = 1,...,M$, resulting in the non-decreasing $\beta _{lk}$. The full Bayesian model with this non-decreasing restriction is

$$\begin{aligned} Y_{i1}&\sim \text {Ber}(\theta _{00}) \text { where } \theta _{00} \sim \text {Beta}(1,1) \nonumber \\ Y_{ij} \mid Y_{i,j-1}&\sim \text {Ber}\left( \theta _{1}(t_j)Y_{i,j-1} + \theta _{0}(t_j)(1-Y_{i,j-1})\right) , ~~ j=1,...,T \nonumber \\ \theta _l(t_j)&= \sum _{k=1}^M\gamma _{lk}F_{k,q}(t_j), ~~l=0,1. \end{aligned}$$

(4)

For the prior distribution of $\gamma _{lk}$, following Shin and Ghosh [11], we consider the following reparametrization,

$$\begin{aligned} \gamma _{l1}=\delta _{l1} \text{ and } \gamma _{lk} = \delta _{lk}\prod _{j=1}^{k-1}(1-\delta _{lj}), ~~k=2,...,m, \end{aligned}$$

which is similar to the stick-breaking representation. Using this reparametrization, $\gamma _{lk}$s satisfy constraint in (3) as long as $\delta _{lk}$s $\in [0,1]$. Therefore, for $\delta _{lk}$, Bernoulli-Beta mixture prior were given that

$$\begin{aligned} \delta _{lk}&= {\left\{ \begin{array}{ll} 0 &{} \text{ with } \text{ probability } 1 - \psi _{lk}\\ \nu _{lk} &{} \text{ with } \text{ probability } \psi _{lk} \end{array}\right. }, \end{aligned}$$

with

$$\begin{aligned} \psi _{lk} \sim \textrm{Beta}(0.5,0.5) \text{ and } \nu _{lk} \sim \textrm{Beta}(1,1). \end{aligned}$$

This representation allows estimating ‘flat’ transition probability curves as $\delta _{lk} = 0$ implies $\beta _{l,k-1} = \beta _{lk}$ for $t \in [t_{k-1},t_k]$. Note that even though the primary focus of this paper is on the non-decreasing constraints, the proposed model would also work for non-increasing constraints with minor modifications by simply redefining the $\gamma _{lk}=\beta _{l,k-1} -\beta _{lk}$.

2.4 Penalized B-Splines

For B-spline basis models, choosing the appropriate number of knots and selecting their locations are not trivial problems. Eilers and Marx [14] proposed penalized B-splines, also known as P-splines, which is a combination of B-spline basis functions and penalization to optimize the number and location of knots. Lang and Brezger [15] extended the P-splines in a Bayesian framework.

Currie and Durban [16] proposed a mixed model approach to estimate the Pspline coefficients, and Kauermann et al. [17] proved the asymptotic properties of P-splines when the number of bases increases with the sample size. Large sample consistencies of the proposed spline-based estimators of the transition probabilities can be established by applying some of the above mentioned methods under both frequentist and Bayesian framework, which we omit in this work and rather our focus is in the finite sample performances of the proposed methodologies using extensive simulation studies that we present later.

Following [16], under a frequentist framework with $E(\varvec{\theta }_l) = g(\textbf{B}\varvec{\beta }_l)$, a general P-spline approach is to find $\varvec{\beta }_l$ such that

$$\begin{aligned} \min ~ \left( \varvec{\theta }_l - g(\textbf{B}\varvec{\beta }_l)\right) ^{\textrm{T}}\left( \varvec{\theta }_l - g(\textbf{B}\varvec{\beta }_l)\right) + \lambda _l \varvec{\beta }_l^{\textrm{T}}\textbf{D}_{\nu }^{\textrm{T}}\textbf{D}_{\nu }\varvec{\beta }_l \end{aligned}$$

where g(x) is a link function and $\textbf{D}_{\nu } \in \mathbb {R}^{(M-\nu )\times M}$ denotes the $\nu$th order difference matrix. For example, the first-order and the second-order difference matrix are constructed as

$$\begin{aligned} \textbf{D}_1 = \begin{pmatrix} -1 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} -1 &{} 1 &{} \cdots &{} 0 &{} 0\\ \vdots &{} &{} &{} &{} \vdots &{} \\ 0 &{} 0 &{} 0 &{} \cdots &{} -1 &{} 1 \end{pmatrix}_{(M-1)\times M}, \textbf{D}_2 = \begin{pmatrix} 1 &{} -2 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} -2 &{} 1 &{} \cdots &{} 0 &{} 0 &{} 0\\ \vdots &{} &{} &{} &{} &{} \vdots &{} \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 1 &{} -2 &{} 1 \end{pmatrix}_{(M-2)\times M}. \end{aligned}$$

In our context of Bayesian Markov models, we extend the logit link model specified in (2) to incorporate P-splines as mixed models, similar to [16]. We represent $\varvec{\beta }_l = \textbf{G}\textbf{b}_l + \textbf{Z}\textbf{u}_l$, where $\textbf{Z}=\textbf{D}_{\nu }^{\textrm{T}} \left( \textbf{D}_{\nu }\textbf{D}_{\nu }^{\textrm{T}}\right) ^{-1} \in \mathbb {R}^{M\times (M-\nu )}$ and $\textbf{u}_l \sim N(\textbf{0}, \sigma _{u,l}^2\textbf{I})$. A common choice of $\textbf{G}$ is $\textbf{G} = \{\textbf{1},\textbf{g},...,\textbf{g}^{\nu -1}\}$ where $\textbf{g} = \{1,...,M\}$. Since it is natural to assume that $\textbf{b}_l$ are independent, we give a prior distribution $\textbf{b}_l \sim N(0,\sigma _b^2)$ with large $\sigma _b^2$. The smoothing parameter $\lambda _l$ is $\lambda _l = 1/\sigma _{u,l}^2$, and we assign a conjugate prior $\sigma _{u,l}^2 \sim IG(a_u, b_u)$. A small $\lambda _l$ indicates undersmoothing, and a large $\lambda _l$ indicates oversmoothing.

The proposed P-splines model with logit link is

$$\begin{aligned} Y_{i0}&\sim \textrm{Ber}(\theta _{00}) \text{ where } \theta _{00} \sim \textrm{Beta}(1,1)\nonumber \\ Y_{ij} \mid Y_{i,j-1}&\sim \textrm{Ber}\left( \theta _{1}(t_j)Y_{i,j-1} + \theta _{0}(t_j)(1-Y_{i,j-1})\right) , ~~ j=1,...,T \nonumber \\ \theta _l(t_j)&= \left[ 1 + \exp \left\{ - \sum _{k=1}^{M}\beta _{lk}B_{k,q}(t_j) \right\} \right] ^{-1}, ~~l=0,1 \nonumber \\ \varvec{\beta }_l&= \{\beta _1,...,\beta _M \} = \textbf{G}\textbf{b}_l + \textbf{Z}\textbf{u}_l. \end{aligned}$$

(5)

The linear link model specified in (1) can also be extended to the P-spline model. However, it is less straightforward than that of the logit link model as the coefficients $\beta _{lk}$s are restricted to be in the interval [0, 1] for (1).

Kauermann et al. [17] proved a general consistency of P-splines for the generalized linear model (GLM) that when the dimension of the spline basis increases as the order of $\mathcal {O}(n^{1/(2q+3)})$ and the smoothing parameter $\sigma _{u,l}^{-2} = \mathcal {O}(n^r), r \le 2/(2q+3)$, under mild regularity conditions, $\widehat{\theta }_l(t_j)$ are consistent estimators of $\theta _l(t_j)$, for $l = 0,1, j = 1,...,T$. Yoshida and Naito [18] discussed asymptotic properties of P-splines in generalized additive models; their approach could be used to establish consistency by utilizing the GLM framework of our proposed model.

2.5 Subject Specific B-Spline Model

In addition to the mean transition probability, one could be interested in estimating the transition probability of a set of specific subjects. Therefore, it is natural to extend the previously proposed models (1)–(5) with an additional hierarchy, assuming that each subject has his/her own transition probability functions which deviate from the mean transition probability. This relationship is analogous to that of population-mean models and subject-specific models from several longitudinal studies [e.g., 19, 20]. This extension allows us to estimate individual-specific transition probabilities as well as overall mean transition probabilities.

Here we only consider the extension of the linear link B-spline model in (1), but other models such as the logit link model or P-spline model can easily be extended. We assume that at time $t_0$, the initial probability of having an event for subject i is $\theta _{i,00}$ such that

$$\begin{aligned} Y_{i0}&\sim \text {Ber}(\theta _{i,00}) \text { where } \theta _{i,00} \sim \text {Beta}(\mu _{00}\tau _0,(1-\mu _{00})\tau _0) \nonumber \\ {}&\mu _{00} \sim \text {Beta}(1,1) \nonumber \\ {}&\tau _0 \sim \text {Unif}(0.1,10), \end{aligned}$$

(6)

where $\mu _{00}$ is the mean of $\theta _{i,00}$, which implies the overall initial probability of having an event across subjects.

For a subject i, let $\theta _{i,1}(t_j)$ denote the true transition probability from 1 to 1 and $\theta _{i,0}(t_j)$ denote the true transition probability from 0 to 1 for $j = 1,...,T$. Then the subject-specific transition probability curve $\theta _{i,l}(t_j), l = 0, 1$ can be written as a linear combination of B-splines basis functions.

$$\begin{aligned} Y_{ij} \mid Y_{i,j-1}&\sim \text {Ber}\left( \theta _{i,1}(t_j)Y_{i,j-1} + \theta _{i,0}(t_j)(1-Y_{i,j-1})\right) , ~~ j=1,...,T \nonumber \\ \theta _{i,l}(t_j)&= \sum _{k=1}^{m_l+q+1}\beta _{i,lk}B_{k,q}(t_j), ~~l=0,1, i=1,...,n \nonumber \\ \beta _{i,lk}&\sim \text {Beta}(\mu _{i,k} \tau _i,(1-\mu _{i,k})\tau _i), ~ \forall i,l,k \nonumber \\ {}&\mu _{i,k} \sim \text {Beta}(a_k b_k, (1-a_k)b_k) \nonumber \\ {}&\tau _i \sim \text {Unif}(0.1,10) \nonumber \\ {}&a_k \sim \text {Beta}(1,1) \nonumber \\ {}&b_k \sim \text {Unif}(0.1,10). \end{aligned}$$

(7)

Similar to (1), the hyper-parameter $\mu _{i,k}$s represent the mean of the subject-specific prior distributions of $\beta _{i,lk}$, and $\tau _i$s control the variance of the distributions. Note that $\mu _{i,k}$ deviates from the common $a_k$ and $b_k$, for all $i = 1,...,n$ and $k = 1,...,M$.

3 Simulation Study

In this section, we conduct multiple sets of simulation studies to evaluate the finite-sample performance of the proposed models. Section 3.1 compares the performance of the B-spline models and that with monotone increasing constraints when the true data were generated from the exponential decay, log-logistic and S/U-shaped functions. In Sect. 3.2, we present the performance of P-spline models with penalties of different orders.

3.1 B-Spline Models

Monte Carlo simulations were conducted to assess the performance of the proposed nonparametric B-spline models and a B-spline model with monotone increasing constraints with two common parametric models, i.e., log-logistic model and exponential decay model. The log-logistic model, which is also known as the Fisk distribution in Economics, is widely used in survival analysis. The transition probability under the log-logistic model is

$$\begin{aligned} \theta _l(t) = (1+\exp (\alpha _l-\beta _l\log (t)))^{-1}, \end{aligned}$$

where $\alpha _l \in \mathbb {R}$ and $\beta _l \ge 0$, $\forall l = 0, 1$. Another popular parametric model is the exponential decay model which is often used to model the decay of a quantity when it decreases at a rate that is proportional to the amount at time t, such as the chemical compound decay. The corresponding transition probability can be written in the form of

$$\begin{aligned} \theta _l(t) = \alpha _l(1-\exp (-\beta _l(t)), \end{aligned}$$

where $\alpha _l \in [0,1]$ and $\beta _l \ge 0$, $\forall l = 0, 1$.

In this simulation, we consider the exponential decay model and log-logistic model as the true transition probability curves. In addition to these concave models, we also consider S-shaped and U-shaped functions to assess the flexibility of our proposed model. We choose the S/U-shaped curves because they resemble the Toenail data that we will analyze in Sect. 4.1. The three sets of underlying true transition probability curves are as follows,

• Exponential decay:

  $$\begin{aligned} \theta _0(t)&= 0.65(1-\exp (-0.1 t))+0.1\\ \theta _1(t)&= 0.85(1-\exp (-0.05 t))+0.1 \end{aligned}$$

• Log-logistic:

  $$\begin{aligned} \theta _0(t)&= (1+\exp (1.5-0.6\log (t)))^{-1}+0.1\\ \theta _1(t)&= (1+\exp (1-0.75\log (t)))^{-1}+0.1 \end{aligned}$$

• S/U-shaped:

  $$\begin{aligned} \theta _0(t)&= 0.04t - 6\cdot 10^{-5} \cdot t^2 + 0.1 \\ \theta _1(t)&= 0.4(0.25\sqrt{t}-0.9)^3+0.3916. \end{aligned}$$

For all three curves, the true intercept is set as $\theta _{00} = 0.1$. The illustration of the true data-generating curves is provided in Appendix A.1

For each true transition probability curve, we fit five different models, i.e., linear link model, logit link model, linear link model with non-decreasing constraints, parametric exponential decay model, and parametric log-logistic model. All models were implemented using the Bayesian MCMC algorithm using R-Jags. All simulations are based on 500 Monte Carlo replications. In each replication, we ran two chains for each model, discarded the first 2,000 iterations of each chain as burn-in, and used the next 8,000 iterations as posterior samples. In order to generate realistic data, we choose the number of subjects $n = 100$ and 12 observed time points after the initial time point, t $= (0,2,4,8,12,20,24,36,44,48,52,56,60)^{\textrm{T}}$, which is motivated from the Toenail data that we will present in Sect. 4.1. For simplicity, all subjects have the same time points. For B-splines, we choose $\lfloor \sqrt{T} \rfloor = 3$ internal knots and cubic splines.

To compare the model fit, the root mean integrated squared error (RMISE), Watanabe–Akaike information criterion [WAIC; 21], and Leave-One-Out information criterion [LOOIC; 22] were computed. The RMISE of an estimate $\hat{\theta }(t)$ is defined as

$$\begin{aligned} \text {RMISE} = \sqrt{\frac{1}{t_T}\int _0^{t_T} \left( \theta (s) - \hat{\theta }(s) \right) ^2ds} \approx \sqrt{\frac{1}{t_T} \sum _{i=1}^h \left( \theta (s_i) - \hat{\theta }(s_i) \right) ^2 \Delta s_i}. \end{aligned}$$

For our simulation, ${t_T} = 60$, and we choose $h = 100$ and equidistant $\Delta s_i$.

WAIC is an extension of the Akaike Information Criterion (AIC) and an improvement of Deviance Information Criterion (DIC) in a fully Bayesian approach. WAIC is obtained as $WAIC = -2(lppd - p_{\text{ waic }})$ where lppd refers to log pointwise predictive density which measures the predictive accuracy of the fitted model [23]. The lppd which is originally defined by the posterior distribution $p(\theta \mid y)$ can be computed using posterior samples $\theta ^{(s)}, s=1,...,S$, by $lppd = \sum _{i=1}^n \log \int p(y_i \mid \theta ) p(\theta \mid y) d \theta \approx \sum _{i=1}^n \log \left( \frac{1}{S} \sum _{s=1}^S\Pr (y_i \mid \theta ^{(s)})\right)$, where n is the number of data points. Moreover, the quantity $p_{WAIC}$ represent the ‘effective’ number of parameters, which measures the complexity of the model. Specifically, as the parameters are random within a Bayesian model, the $p_{WAIC}$ approximates the number of unconstrained parameters in the model; each parameter counts as 1 if it is estimated with no constraints or weakly informative prior, 0 if fully constrained or prior distributions are informative, or an intermediate value if in between them [24]. The quantity is calculated as $p_{\text{ waic }}= \sum _{i=1}^nVar_s(\log (\Pr (y_i \mid \theta ^{(s)})))$, with $Pr(y_i \mid \theta ^{(s)})$ representing the posterior predictive likelihood. WAIC is a more robust criterion compared to AIC and DIC, as it averages over the posterior distribution. Alternative to WAIC, Vehtari et al., [22] approximate Leave-One-Out CV (LOOCV) using importance weights. Even though WAIC is asymptotically equal to Leave-One-Out CV, according to [22], the LOOCV approach could be more robust. Note that the model with a small value of the RMISE, WAIC, or LOO is considered to be better in terms of model fit.

All of the previously mentioned criteria, however, do not take into account the auto-correlative characteristics of the Markov models. Therefore, we consider another criterion suggested by Geweke and Amisano [25] that evaluates the predictive performance of the sequential prediction. Specifically, the one-step-ahead predictive likelihood at time t is defined as

$$\begin{aligned} PL(t){} & {} = p(y_{t+1}\mid y_{1:t}) = \int p(y_{t+1} \mid y_{1:t}, \varvec{\theta })p(\varvec{\theta } \mid y_{1:t})d\varvec{\theta } \\{} & {} \approx \frac{1}{S}\sum _{s=1}^S p\left( y_t \mid y_{1:t}, \varvec{\theta }^{(s)} \right) . \end{aligned}$$

Consequently, we define the one-step-ahead negative cumulative log predictive likelihood (NCLPL) as

$$\begin{aligned} \text{ NCLPL } = - \sum _{t=H+1}^{T-1} \log PL(t), \end{aligned}$$

where H is a pre-specified time point. A model with the smaller $\text{ NCLPL }$ better explains the data.

Moreover, since we make predictions of binary outcomes, we compare the accuracy of our prediction which is the proportion of correct prediction out of total prediction. By averaging by the number of subjects and the number of MCMC samples S, the accuracy is calculated as

$$\begin{aligned} \text{ Accuracy } = \frac{1}{nS(T-H)} \sum _{s=1}^S \sum _{i=1}^{n} \sum _{t=H+1}^T I\left( y_{it} = \hat{y}_{it}^{(s)}\right) , \end{aligned}$$

where $y_{it}$ denotes the observed outcome of subject i at time t, and $\hat{y}_{it}^{(s)}$ denotes the predicted value of the sth MCMC sample. In order to be consistent with other model fit criteria that the smaller value implies the better fit, we calculate the error rate defined as 1-Accuracy. For the NCLPL and error rate, we set $H = T - 4$.

Figure 2 displays the simulation results with boxplots based on 500 Monte Carlo repetitions; the numerical results are provided in Appendix A.1 The LOOIC and WAIC show very similar results. When the true transition probability curves are exponential decay or log-logistic, then parametric models show the smaller WAIC, LOOIC, RMISEs, NCLPL, and error rate, as expected. In fact, exponential decay or log-logistic have similar concave shapes, and we found that the log-logistic model performs well under both exponential decay and log-logistic true curves. The proposed nonparametric models showed comparable performance. Particularly, the linear link model with non-decreasing constraints showed better performance than models without the constraints and sometimes even better than parametric models.

On the other hand, when the true transition probability curves are S-shaped or U-shaped, i.e., if the true curves do not have concave shapes, the performance of the parametric models is poor. The nonparametric model with non-decreasing constraints estimates $\theta _{1}$ well but did not for $\theta _{0}$, as the former has non-decreasing increasing shapes whereas the latter does not. These simulation results show the robustness of our nonparametric models regardless of the shape of true functions, whereas parametric models showed poor performance when the model is misspecified. Also, the nonparametric model with non-decreasing constraints shows the best performance in general under all three scenarios where the true probability curves are non-decreasing.

Fig. 2

Boxplots of various model evaluation criteria under three different true models; a Exponential Decay, b Log-Logistic, c S/U shaped

3.2 Knot Selection

In this section, we compare the model fit of the proposed P-spline models to assess the appropriate number of internal knots and orders of penalty. The data sets are generated from the following transition probability curves when $t \in (0,100]$,

• $\theta _0(t) = 0.9 - 0.8 \left[ 1+\exp \{-1.5\cos (3\pi t/50)\}\right] ^{-1}$

• $\theta _1(t) = 1-\left[ 1+\exp \{1.5\sin (4\pi \times (t+5)/50)\}\right] ^{-1},$

and $\theta _{00} = \theta _0(0) = \theta _1(0) = 0.2$. The illustration of the true transition probability curves is provided in Appendix A.2. Given the number of subjects $n = 100$ and the time range $t \in [0,100]$, we choose the number of distinct time points $T = 25$ where $\textbf{t} = (t_1,...,t_T)$ are equidistant in [1, 100], and $t_0 = 0$.

We compare the model fit of the P-spline model with different orders of penalty, i.e., no penalty and penalties of orders 1, 2, and 4. For each penalty level, we consider internal knots with four different sizes, 5, 10, 15, and 20. We use the same five model comparison criteria in Sect. 3.1 based on 500 Monte Carlo repetitions. In addition to the one-step-ahead PL, we consider d-step-ahead prediction and compare the corresponding NCLPL and error rate. The d-step-ahead predictive likelihood at time t is calculated as

$$\begin{aligned} PL_d(t) = p(y_{t+1:t+d}\mid y_{1:t}) \approx \frac{1}{S}\sum _{s=1}^S p\left( y_{t+1:t+d}\mid y_{1:t}, \varvec{\theta }^{(s)} \right) . \end{aligned}$$

and similarly,

$$\begin{aligned} \text{ NCLPL}_d = - \sum _{t=H}^{{T-d}} \log PL_d(t). \end{aligned}$$

We set $H = T - 4$ and $d = 4$. The average error rate at each predicted time point $H+1$,...,$H+d$ is also calculated.

Fig. 3

Boxplots of various model evaluation criteria under different number of internal knots

Figures 3 and 4 display the results with boxplots; numerical results are provided in Appendix A.2. Under the small number of internal knots, the model with no penalty performs the best, and under the large number of internal knots, the model with a high order of penalty performs well in general. The performance of all four models under the internal knots of size 5 is relatively poor compared to the higher number of internal knots. However, all models show similar performance when the number of internal knots is greater than 10. Under each of the different internal knot settings, the model with penalty order 2 performs the best in general. Figure 4 illustrates the 4-step-ahead error rate at each time point under the different number of internal knots. As expected, the error rate increases as we predict the later time point, and the model with the penalty order of 2 shows the smallest increase in general. Therefore, from the simulation, the number of the internal knot around 10 was found to be sufficient, and the model with the penalty order of 2 was found to be the best in general.

Fig. 4

4-step-ahead error rate comparison under different number of internal knots

4 Real Data Analysis

In this section, we apply the proposed models to analyze two data sets, the toenail clinical trial data and the Dow Jones data, a stock market index.

4.1 Toenail Data

We first analyze a randomized clinical trial comparing two competing oral treatments, Terbinafine and Itraconazole, for toenail infection. Details of the study are described in De Backer et al. [26], and the dataset is available from R-package HSAUR3. The dichotomous outcome variable is the severity of toenail infection, with 0 denoting a moderate or severe symptom and 1 denoting a none or mild symptom. Patients had oral treatments for 12 weeks, and the follow-up visits were scheduled at weeks 4, 8, 12, 24, 36, and 48. Among 294 enrolled patients, 148 patients were on Terbinafine and 146 patients were on Itraconazole; the data are not complete as 31 patients on Terbinafine and 29 patients on Itraconazole did not complete all seven scheduled visits.

We are interested in analyzing the probability that the toenail infection is mitigated after treatment begins for each treatment. Let’s define $\varvec{\theta }_{ab}(t)$ be the transition probability from status a to status b at time t. Among the four possible transition probabilities, the most interesting one is $\varvec{\theta }_{01}(t)$, which indicates the transition probability from moderate or severe to none or mild at time t. In addition, $\varvec{\theta }_{11}(t)$, the probability of continuing to have none or mild symptom, is also our interest.

We used the proposed B-spline model with the linear link, the B-spline model with non-decreasing restriction, and the subject-specific B-spline model to fit the data. The monotone increasing assumption is reasonable because the probability of getting better would increase as patients kept receiving treatments. For both treatments, cubic splines with m internal knots are used, where $m = \lfloor \sqrt{6} \rfloor = 2$. Two chains were used, and for each chain, 25,000 MCMC samples were used for posterior inference after discarding the first 5,000 samples.

For the model fit comparison, note that RMISEs cannot be computed for real data as we do not have true parameter values unless we use cross-validation my holding out data. On the other hand, we provide several predictive criteria to evaluate the model performance that can be computed based on real data. Similar to the simulation studies in Sect. 3, we compared model fits using the WAIC, LOOIC, NCLPL, and error rate. Due to the small number of visits, we conducted one-step-ahead predictions from visit 5 (week 24) to visit 7 (week 48). Table 1 shows the model fit comparisons for the toenail data. The error rate is the average of three one-step-ahead predictions. For Terbinafine, the linear link B-spline model was found to be the best model, whereas for Itraconazole, the subject-specific model was the best. Figure 5 shows the estimated transition probability curves from moderate or severe to none or mild and continuing to have none or mild symptom, using the selected model, i.e., the linear link model for Terbinafine and subject-specific model for Itraconazole. For the transition probability from moderate or severe to none or mild, both treatments show increasing trends at first and then decreasing. These trends are reasonable because the patients were on treatments for 12 weeks, and their symptoms were measured during and afterward. On the other hand, the transition probabilities of continuing to have none or mild symptom are very high for both treatments. In both cases, it can be seen from the wide overlapping credible intervals that the two treatments are comparable.

Table 1 Model fit comparisons for toenail dataset; bold numbers imply the best model fit, i.e., the smaller the better

Fig. 5

Estimated transition probabilities curves of two treatments; a transition probabilities from moderate or severe to none or mild, b probability of continuing to have none or mild symptom

4.2 Dow Jones Index

In Econometrics, a Markov model has been widely applied to analyze stock price index data. Hamilton [27] initially proposed an auto-regressive framework using a first-order Markov chain and extended it with an autoregressive conditional heteroskedasticity [28]. De Angelis and Pass [29] proposed a framework to investigate the dynamic patterns of stock markets by exploiting the latent Markov model and applied this framework to the U.S. stock market indices. Similarly, Sasikumar and Abdullah [30] used Hidden Markov Model to make inferences regarding stock market trends, and Cheng et al. [31] proposed a state-varying endogenous regime-switching model and analyzed Chinese stock market returns.

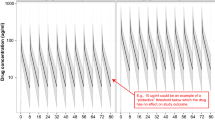
One of the most commonly used stock indices is the Dow Jones Industrial Average which measures the stock performance of 30 blue-chip companies in the USA. It is one of the most-watched stock indexes in the world, containing companies such as Apple, Boeing, Microsoft, etc. [32]. Our analysis is based on daily log returns for the 30 companies in the Dow Jones Index, defined as $lr(t) = \log (p_{t}/p_{t-1})$,where $p_t$ denotes the price of the stock on day t. The data set is obtained from get.hist.quote function in R-package tseries for the period from July 1, 2019 to November 15, 2020, which includes $T = 348$ time points. Figure 6 illustrates the trend of daily log returns of each stock included in the Dow Jones Index, which shows high volatility that makes it difficult to assess the stock trend.

Fig. 6

The trend of daily log returns of each stock included in the Dow Jones Index from Jul. 2019 to Nov. 2020

We applied the proposed Markov models to investigate the behavior of the 30 blue-chip companies included in the Dow Jones Index. In particular, we are interested in the behavior in terms of “safety” during the recent COVID-19 pandemic. In this regard, two states of log return are defined as loss - “negative or zero log return” or gain - “positive log return”. The zero return can be considered the negative return because it is the loss of money considering that one could earn at least some interest instead if one had deposited the money in the bank account.

Using R-jags, we fitted four different models; the linear link model, the subject-specific linear link model, and the penalized B-spline model with penalties of orders 1 and 2. We ran two chains for each model, discarded the first 5,000 iterations of each chain as burn-in, and used the next 10,000 iterations as the posterior sample. For the B-spline models (the first and the second models), we used $\lfloor \sqrt{T} \rfloor = \lfloor \sqrt{348} \rfloor = 18$ internal knots, and for the P-spline models (the third and the fourth), we used 35 internal knots. Similarly to Sect. 3, we use the WAIC, LOOIC, NCLPL, and error rates to compare the model fit. For NCLPL, in addition to the $\text{ NCLPL}_1$ with one-step-ahead predictions, we conduct five-step-ahead predictions and calculate the $\text{ NCLPL}_5$, since the week ahead prediction is one of the common interests in the stock market. With $H = {T - 10}$, the $\text{ NCLPL}_1$ is the sum of 10 one-step-ahead predictions, and the $\text{ NCLPL}_5$ is the sum of 6 five-step-ahead predictions. For error rates, we use $H = {T - 10}$.

Table 2 Model fit comparisons for the Dow Jones Index data; bold numbers imply the best model fit, i.e., the smaller the better

Fig. 7

Estimated transition probability curves and 95% credible intervals from the P-spline model with order 1

Table 2 compares the model fits of the four models. All five criteria suggest that the P-spline model with the order of 1 is the best model to fit the Dow Jones data. Figure 7 illustrates estimated transition probability curves and 95% credible intervals from the P-spline with order 1 model. The solid black lines indicate the transition probabilities of the overall Dow Jones Index, and the dashed lines represent the 95% upper and lower credible bounds. Blue areas indicate the periods when the estimated curves are greater than 0.5 with 95% probability, and red areas indicate the period when the estimated curves are less than 0.5 with at least 95% probability.

Fig. 8

Estimated overall mean vs. individual stock transition probability curves using the subject-specific model; a transition probability from loss to gain, b probability of being gain

The upper plot presents the estimated transition probability curves from the loss stage to gain stage. In general, the overall Dow Jones Index shows a high transition probability from the loss to gain, since the estimated transition probability is around or greater than 0.5 in general. The periods with high transition probability from loss to gain include ‘2019-08-12 - 2019-09-11’, ‘2020-03-16 - 2020-04-20’, ‘2020-06-26 - 2020-07-17’, and ‘2020-09-25 - 2020-10-15’. The bottom plot represents the estimated probability curve of being gain stage. The overall trend shows that Dow Jones Index is a safe index since the probability is around 0.5 or greater. However, in the period of ‘2020-02-13 - 2020-04-09’, the probability of being gain was less than 0.5, with the lowest probability of 0.13 (95% CI: 0.09 - 0.19) on ‘2020-03-09’. This could be due to the anxiety about the pandemic since COVID-19 started widely spreading in this period.

If one is interested in estimating the trend of an individual stock, the proposed subject-specific model allows estimating the individual transition probability curves as well as the overall transition probability curves. Figure 8 shows the estimated overall mean vs. individual stock transition probability curves using the subject-specific model. The colored curves are the transition probabilities of individual stocks, and the black curves are the overall mean probability curves. While the behavior of 30 stocks is similar to the overall mean in general, these individual stock transition probability curves enable us to identify which stocks are safer and which are riskier than other stocks.

Fig. 9

True transition probability curves under three different scenarios; exponential decay, log-logistic, and S/U shaped

Table 3 Simulation results under three sets of true transition curves; bold numbers imply the best model fit, i.e., the smaller the better

Fig. 10

True transition probabilities for knot selection

Table 4 Simulation results under the different number of internal knots; bold numbers imply the best model fit, i.e., the smaller the better

5 Discussion

In this paper, we have proposed a flexible Bayesian nonparametric approach for nonhomogeneous Markov model when the response variable is autocorrelated and dichotomous. We use B-spline basis functions to reduce the number of parameters to estimate, and also to estimate smooth transition probability curves. Our model allows imposing non-decreasing restrictions or estimating individual-specific curves. Simulation studies show the robustness of our models under the various shapes of the true transition probability functions.

Within a frequentist framework, our proposed models can possibly be estimated using some optimization methods, e.g., the popular quadratic programming method as we have illustrated (see Sect. 2.4). However, as is well known the frequentist framework is particularly complicated when faced with missing (or censored) values in the data. Whereas within a Bayesian framework, under the usual assumption of missing at random (MAR), the posterior predictive distribution of the missing (or censored) values conditional only on the observed values can be sampled easily to do the imputation on the fly while drawing samples from the posterior distribution. Moreover, within a Bayesian framework the quantification of uncertainty (e.g., standard errors) of the parameter estimates can be obtained rather easily; and in fact the entire posterior or predictive distribution can be estimated using the samples generated by the MCMC methods.

Our proposed models are based on the nonhomogeneous Markov assumption of the binary response $Y_t$. It is natural to extend these models under the hidden Markov assumption [see, e.g., 33] that the Markov process is not observable. Also, under the assumption of the non-decreasing transition probability curves, we impose monotone increasing shape restrictions. To better estimate the true curves, other shape constraints such as convex, concave, S-shaped, and U-shaped, can also be imposed, [e.g., 34], based on subject matter knowledge. As mentioned earlier, the primary focus of this work is to explore the finite sample performances of the proposed dynamic models for transition probabilities, but it would be desirable to establish theoretical large sample properties of the proposed estimators under some technical regularity conditions by applying some of the existing theory for penalized splines models. However, verification of such technical conditions is often not possible in practice, especially those that are based on realistic scenarios.

Details of Simulation Studies

This section provides additional details of the simulation studies in Sect. 3, including the illustration of the true data generating functions and the numerical results of the simulation studies.

1.1 Details of the Simulation of the B-Spline Models in 3.1

Figure 9 illustrates the three underlying true transition probability curves for simulation studies of the B-spline models in section 3.1. Solid dots indicate the 13 observed time points.

Table 3 summarizes the simulation results based on the model fit criteria described in 3.1. The average WAIC, LOOIC, RMISE, NCLPL, and error rate are summarized with corresponding Monte Carlo standard errors in the parenthesis. Similar to Fig. 2, parametric models show better model fits when the true transition probability curves are exponential decay or log-logistic. However, the proposed B-spline basis models show comparable performance. On the other hand, when the true transition probability curves have non-concave shapes such as S-shaped or U-shaped, the nonparametric B-spline models significantly outperform the parametric models.

1.2 Details of the Simulation of Knot Selection in 3.2

Figure 10 illustrates the true transition probability curves to evaluate the performance of P-spline models in 3.2.

Table 4 summarizes the simulation results. Analogous to Fig. 3 and Fig. 4 in the main paper, P-spline models with higher orders of penalty perform better under a large number of internal knots. The internal knot of size 10 was found to be sufficient, and the P-spline model with penalty order 2 performs the best in general.