1 Introduction

Energy efficiency with high speed in low-power ultra-large-scale integrated circuits has attracted the attention of researchers in the nanometer regime according to [1], as this is the prime need for modern electronic devices to prolong the battery life. The feature size of metal oxide semiconductor devices is improving (miniaturization) day by day consequently. With improved scaling in deep sub-micrometer regime, leakage current is becoming considerable, as it contributes a sizable fraction to the total power dissipation of a chip mentioned in [2]. The low-power electronic industry is progressing by leaps and bounds with the high demand for portable electronic devices. These devices consist of high-speed data processors that perform complex operations employing MOS as fundamental blocks. Large-scale industrial automation, space applications, image processing, modern warfare industry, biomedical implantable devices, and other modern miniaturized electronic devices consist of digital signal processing (DSP) units [3]. These units are used to perform arithmetic and logical operations utilizing multiplier and high-speed adders. Therefore, the selection of adder topologies becomes the prime concern for the designer to make the system energy efficient with high speed, particularly in multipliers. Various increasing limitations of decreasing nanometer technologies have attracted the researcher’s attention to the search for new hybrid circuits and techniques for electronic devices. The adiabatic logic technique is one of the prominent techniques of power reduction [4]. In the literature, various techniques have been reported which are used to implement the adders for modern electronic systems. Some have limitations of the area, and some other has limitations of delay, capacitance, and swing in output voltage [5]. Conventional static CMOS-based circuits occupy a large area of the chip and increased leakage currents with improved scaling. A hybrid adder based on complementary pass transistor (CPL) logic has been reported in [6]. In this circuit, the first part consists of X-OR/ X-NOR which consists of NMOS with one inverter. Reduced delay in this circuit is advantageous, but it dissipates more power as in [7] and [8]. An approximate 4–2 compressor circuit has been reported in [9] which reduces the number of adders required, but approximate compressors are erroneous. A fourth passive element memristor-based adder has been presented in [10] with some constraints such as commercial availability and speed as compared to MOS devices. Another hybrid full adder with a strong driver and good voltage swing has been reported in [11]. However, the functioning of hybrid adders requires less power, but their decreased speed and increased number of transistors become a constraint for high-frequency computations [7]. In this paper, the novelty of these new proposed designs of full adder circuits is based on parallel computing. These adders compute the sum parallelly which results in very high speed with reduced power dissipation. In A-I, carry is separately computed with three transistors-based X-OR gate [12] and multiplexer (MUX). In the second design A-II, two-phase clocked adiabatic static CMOS logic (2PASCL) [13] has been used, whereas A-III computes carry and sum both parallel.

2 Fundamental concepts and related terminologies

2.1 Mechanism of power dissipation in a CMOS

There are three dominant sources of power dissipation in a MOS device, which are responsible for the draining of the battery. This dissipated power further increases the temperature of the integrated circuits. This increased temperature affects the performance of the device in ON and OFF states [14] and [15].

Total power dissipation in a MOS device is the combination of these three components [16] .

  • Dynamic power dissipation

  • Short circuit power dissipation

  • Static power dissipation.

$$P_{T } = {\text{P}}_{{\text{D}}} + {\text{P}}_{{{\text{SC}}}} + {\text{P}}_{{\text{S}}}$$
(1)

where PT is the total power dissipation of a MOS device.

2.2 Logical composition of full adder

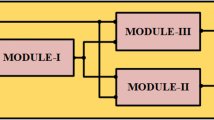
Logically the architecture of full adder consists of three blocks as shown in Fig. 1. It consists of three modules: the first module consists of X-OR/X-NOR gates and second consists of X-OR/X-NOR/multiplexer (MUX) which gives a final sum with a MUX for carry generation. Functionally full adder has three inputs bits (A, B, Cin) and gives two outputs sum and carry out as shown in Fig. 1. Truth “Table 1” represents all possible three-bit combinations of A, B, and, Cin as input with sum and carry as output for a full adder. The basic functionality of a full adder in terms of its input and outputs is governed by the following equations.

$$Sum = A \oplus B \oplus Cin$$
(2)
$$Carry = (\overline{A\Theta B) \times } C + (A\Theta B)\, \times\, A$$
(3)
Fig. 1
figure 1

Basic structure of full adder

Full size image
Table 1  Truth table of full adder
Full size table

2.3 Adiabatic logic and 2PASCL

Adiabatic fundamentally represents the recycling of stored charge at capacitive nodes. For charging and discharging of a conventional CMOS inverter, the output node capacitance (C) needs some energy equivalent to CV2dd from the power supply where Vdd is the supply voltage. Half of this energy 1/2CV2dd is stored by the node capacitance, and the rest half is dissipated by the PMOS ON state resistance during the charging of node capacitance [4]. The stored energy in node capacitance goes to the ground through NMOS during the discharging process and wasted away, whereas in adiabatic logic circuits, this stored energy recycled back to the power supply which decreases power consumption. Charging and discharging adiabatically can be represented by an RC model as shown in Fig. 2.

Fig. 2
figure 2

Adiabatic charging

Full size image

The node capacitance in this RC model is represented by C which is charged through a MOS transistor, whereas R represents the ON-state resistance of MOS with a constant current source I(t) which is used to charge the capacitance instead of a fixed voltage Vdd in CMOS inverter. Assuming the initial charge on the capacitor is zero then the voltage across capacitor Vc(t) is given by the following expression

$$V_{c} (t) = \frac{1}{C}i(t) * t$$
(4)

and,

$$i(t) = C\frac{{V_{c} (t)}}{t}$$
(5)

The energy dissipation can be approximated by the following equation

$$E_{{{\text{diss}}}} = R\int\limits_{0}^{T} {i^{2} (t)dt = Ri^{2} (t) * T = \frac{{{\text{RC}}}}{T}{\text{CV}}_{c}^{2} (T)}$$
(6)

where Vc(T) is the voltage across the capacitor for time T. It is depicted from “Eq. (6)” that the energy loss can be decreased by keeping T > 2RC as compared to conventional charging at Vdd supply voltage. Further, the energy loss can be minimized by reducing R and by using a slowly time-varying voltage supply, i.e., by increasing T.

The operation of basic CMOS inverter using 2PASCL [13] can be explained with the help of Fig. 3. Here, two extra MOS transistors are used with complementary power supply clocks PC and \(\overline{{{\text{PC}}}}\). Both power clock supplies are complementary with each other, and the voltage magnitude of both power clock supplies is governed by “Eqs. (7) and (8)” [13].

$$V_{{\text{PC }}} = \, \frac{{V_{{{\text{DD}}}} }}{4}\sin (\omega t + \theta ) + \frac{3}{4}V_{{{\text{DD}}}}$$
(7)
$$V_{{\overline{{{\text{PC}}}} }} = \, \frac{{V_{{{\text{DD}}}} }}{4}\sin (\omega t + \theta ) + \frac{1}{4}V_{{{\text{DD}}}}$$
(8)
Fig. 3
figure 3

a 2PASCL-based inverter b Power clock supplies

Full size image

The magnitude of \(V_{{{\text{PC}}}} V_{{{\text{PC}}}}\) is twice of \(V_{{\overline{{{\text{PC}}}} }} V_{{\overline{{{\text{PC}}}} }}\) to reduce the voltage difference between the electrodes which results in decreased power dissipation. In the proposed circuit split level clock supply charges/discharges the load capacitance slowly as compared to other clock pulse used in adiabatic logic. This also minimizes energy loss. The operation of this circuit is divided into two steps, i.e., evaluation and hold.

  • During evaluation when output is low and pull-up network turns ON, the load capacitance CL charged through PMOS and output goes HIGH. When the output is high and pull-down network turns ON, discharging of load capacitance takes place via NMOS and D2.

  • In the hold step, if no transition takes place at the input side, the output will be held by the load capacitance, consequently, reduces switching activity and results in decreased energy loss.

3 Proposed work and logical composition of full adder

The proposed logical structure of the full adder is shown in Fig. 4. The sum has been computed in a single module without any gate as compared to the conventional three-module approach as shown in Fig. 4a. Carry generation has been achieved separately by using the conventional method with the X-OR gate and with adiabatic logic circuit also following the logical structure given in Fig. 4b. In A-II, adiabatic logic has been used to increase the power efficiency. Two more transistors have been used in A-II as compared to A-I. In the proposed design A-III carry generation has been achieved parallelly as shown in Fig. 4c.

Fig. 4
figure 4

Logical composition of proposed full adder design, a for SUM, b for conventional carry, c for parallelly computed carry

Full size image

3.1 Proposed adder–I (A-I)

The proposed design of full adder (A-I) is shown in Fig. 5. In this proposed architecture, all the inputs are applied simultaneously and SUM is computed in a single module parallelly with only two-transistor delay. Carry generation has been achieved with the help of the 3 T X-OR gate and MUX. The design consists of a series of complementary transistors, two PMOS for the upper part, and two NMOS below the PMOS. The operation of the circuit is based on the working of the pass transistor. Operation of this design can be explained as; if the input combinations A, B, and Cin are 110 applied, then the transistor P1, P2 will be OFF and Cin is low; therefore, whatever charge is present at SUM node will be pulled down through the ON transistors N1, N2 by Cin and SUM will be computed zero. Following this operation, we can verify all three-bit (A, B, Cin) possible input combinations for SUM. This design requires twenty-one transistors which is less than conventional CMOS-based design.

Fig. 5
figure 5

Full adder design for A-I

Full size image

3.2 Proposed adder–II (A-II)

In this approach, two-phase clocked adiabatic static COMS logic has been used and the architecture is given in Fig. 6. Two more transistors have been used in addition to the architecture used in A-I. The working for SUM computations is the same as explained in the previous design. Operation of carry generation using adiabatic logic reduces the power requirement up to a great extent, and its operation is based on the inverter operation which is explained in Sect. 2.3 with the help of Fig. 3. Two-phase clocked supply has been used as PC and \(\overline{{{\text{PC}}}}\); both are complementary with each other. The magnitude of \(\overline{{{\text{PC}}}}\) has been kept half as that of PC to reduce the difference in node voltages and consequently reduces power dissipation. In Fig. 6, we have used the SPICE-based Mentor EDA tool for simulating the circuit. It is used due to the only available licensed simulating software that can be accessed by a research scholar in our university.

Fig. 6
figure 6

Full adder design for A-II

Full size image

3.3 Proposed adder–III (A-III)

This approach used the idea of parallel computing for carry generation as shown in Fig. 7. In this design, carry is generated parallelly which takes maximum three transistor delay which increases speed. The operation of this circuit is based on the working of the pass transistor. It can be explained as follows: if the input combination for A, B, and Cin is 111, then the transistors N10, N11, N12 will be ON and all PMOS except P12 and P13 will remain OFF. Therefore the “carry1” node will be pulled up by Cin through N10, N11, N12 and carry output will be computed as “1” which is theoretically expected. However, the penalty for increased transistor count has been overcome with fast speed. Buffer has been used to increase the drive capability which also provides full voltage swing at the carry output.

Fig. 7
figure 7

Full adder design for A-III

Full size image

4 Results and performance analysis of proposed designs

The proposed designs have been simulated in 0.18 µm CMOS technology. All the proposed designs have been simulated with varying supply voltages and temperatures. Obtained results of the proposed designs in terms of power, delay, and PDP are given in the tabular form and also analyzed graphically. The carry generation path is the longest in all designs; therefore, the delay for carry generation has been considered for all designs for the worst-case delay. Table 2 shows the obtained results for A-I and A-II with a varying supply voltage of 1.2 to 2.4 V, whereas Table 3 represents the results with varying temperatures (10 to 45 °C).

Table 2 Power, delay and, PDP results with varying supply voltage
Full size table
Table 3 Power, delay and, PDP results with varying temperature
Full size table

Figures 8 and 9 show the power delay product (PDP) which is considered a figure of merit for the electronic circuits. Figure 8 shows the effect of varying supply voltage on PDP, whereas Fig. 9 shows the effect of varying temperature on PDP.

Fig. 8
figure 8

PDP results of A-I and A-II with variable supply voltage

Full size image
Fig. 9
figure 9

PDP results of A-I and A-II with varying temperature

Full size image

The results in terms of power, delay, and PDP for the proposed design A-III are tabulated in Tables 4 and 5. It is depicted from the tabulated data in Table 4 that carry has been computed at very high speed with a delay of 2.33 ps without a buffer at the standard supply voltage of 1.8 V. Table 5 shows the power and delay results with varying temperature conditions. However, the insertion of buffers increases the delay and area, but it restores the signal swing which proves the good drive capability and functionality of the proposed design.

Table 4 Power, delay and, PDP results with varying supply for A-III
Full size table
Table 5 Power, delay and, PDP results with temperature for A-III
Full size table

The effect of buffer insertion on delay is depicted in the given figures below. Figure 10 shows that the proposed design achieved very high speed utilizing parallel computing concepts with varying voltage, whereas Fig. 11 shows the delay with and without buffer with varying temperatures.

Fig. 10
figure 10

Delay trends with varying voltage

Full size image
Fig. 11
figure 11

Delay trends with varying voltage for A-III

Full size image

4.1 Comparison with existing designs

The proposed designs have been compared with best-reported designs in literature in terms of device count, power, delay, and PDP with technology. The proposed designs show better performance in terms of speed and power. Table 6 shows the comparison with existing designs.

Table 6 Comparison with existing designs
Full size table

The performance of the proposed designs has been compared and represented graphically as shown in Fig. 12 based on average power, worst-case delay, and technology used. It is depicted from Fig. 12 that the proposed designs perform better as compared to the latest designs reported in the literature.

Fig.12
figure 12

Comparison with existing designs in terms of avg. power, delay and, technology

Full size image

4.2 Waveforms

The output waveform in Fig. 13 given below clearly shows that the signal swing achieved is sufficient for switching purposes. Figure 13a shows graphically all the three-bit possible combinations for a full adder, whereas Fig. 13b shows the output logic waveforms of the proposed circuit A-I for carry and sum. Figure 13c represents the output logic waveforms of proposed circuit A-II for carry and sum. Figure 13d shows the output logic waveforms of proposed circuit A-III for V(carry) and sum, whereas V(carry2) represents the output with buffer and restores the logic completely. Output waveforms of simulated circuits verify the functioning of the proposed design with output voltage level, above 1.14 V for high logic, and below 0.78 V for low logic, which is sufficient for adiabatic logic families for digital switching circuits as reported in the literature.

Fig. 13
figure 13

Waveforms of a Three-bit input combinations, carry and the sum of a full adder with b A-I c A-II d A-III

Full size image

5 The layout of the proposed design A-III

The layout of the proposed design A-III has been generated according to the flowchart as given in Fig. 14. The layout of the new design A-III has been simulated to verify the functionality of our proposed logic of parallel computing. Figure 15 shows the layout of design A-III with an area of 192.68 µm2 including a buffer. Post-layout design A-III consumes the power of 0.526 µw with a delay of 64.23 × 10–3 ns with a buffer with 1.8 V supply. This layout has been designed using HSPICE and at 0.18 µm technology. This software and technology have been used as at this technology node the leakage currents are less as compared to small technology nodes.

Fig. 14
figure 14

Flowchart of layout generation

Full size image
Fig. 15
figure 15

The layout of design A-III

Full size image

6 Conclusion

In this article, implementation of parallel computing with adiabatic logic has been demonstrated for full adder designs. The work done in this article has been simulated in 0.18 µm CMOS technology. The proposed approach mitigates the issue of large propagation delay and achieves a signal restoration with a buffer. The presented designs perform better in terms of power dissipation, delay, and the number of transistors used as compared with the existing designs which are reported in the literature. It is evident from the results that the overall power efficiency of the proposed designs is good as compared to existing designs. Implemented new circuits work fairly with varying voltage and temperature conditions. The proposed designs with adiabatic logic also perform better with sufficient output voltage levels. These improvements in performance with high speed make proposed full adders better candidates for ultra-low-power applications. As a future work, author is working actively toward the implementation of this approach in sequential circuits.