1 Introduction

The dynamic relationship between predators and their prey has been one of the dominant themes in mathematical ecology. A major concern is to understand how the population of a given species influences the dynamics of other species. Organisms at the lowest trophic levels have to deal with a high risk of predation and to defend themselves against predation which is the main driving force in their evolutionary histories [1]. Planktons are the basis of the aquatic food chain, and its importance for the marine ecosystem is widely recognized [2]. Antigrazer responses of phytoplankton have been widely documented and vary with external abiotic factors [3]. Algal species are highly flexible in their morphology, growth and production of toxin and deterrent compounds and have been interpreted as defense mechanisms against grazing [4]. Production of toxin has great impact on phytoplankton–zooplankton dynamics [5,6,7]. A study demonstrates that the toxin-producing antipredator defense by phytoplankton may sometimes act as a biocontrol by the stabilizing effect towards the plankton population [8]. Bloom of such algal and fish predation on zooplankton has a strong negative effect on zooplankton and marine ecosystem.

Diel vertical migration (DVM) of zooplankton may be one of the most widely studied defensive strategies [9,10,11]. But at high predation risk, zooplankton benefits from antipredator defense such as morphological, behavioral, or life history changes to balance the reduction in growth [12, 13]. The ability to defend from predator attack is an important trait shaping individual fitness, population dynamics and, in consequence, the structure of zooplankton communities [14]. But it has been observed that certain adaptations such as dormancy enable the organism to reduce and manage the environmental stress [15,16,17]. Adapting dormancy for the evolution of zooplankton is sometimes beneficial to maintain the optimal population size in the environment, i.e., its carrying capacity [19, 20]. The capability of prey towards the defense provides a new area to analyze the prey–predator model more closely [21, 22]. An experiment shows that at high concentration of filamentous blue-green algae, the reproduction of Daphnia ceases and its population disappears from the environments in few days [23].

One more important parameter that may cause instability and influctuation in stable equilibrium is a time delay relevant for the large number of biological systems; for example, some time is required to digest food by the animals before further activities [24,25,26]. Time delay affects the stability of positive equilibrium which fluctuates the population causing Hopf bifurcation [28]. It has been observed that time delay has a great influence in any biological process and increasing its value may cause a stable equilibrium to unstable or fluctuation in population [29, 30]. Rehim and Imran [31] investigated the impact of gestation delay on the phytoplankton–zooplankton system which initially imparts stability and then makes the whole system unstable. Recently, a delayed nutrient cycle model for the plankton system elaborated that delay in decomposition of litter does not influence the stability of the system [32]. Singh and Gakkar [33] observed the rich dynamics including chaos in discrete time delay toxin-producing phytoplankton–zooplankton dynamics. From the last two decades, the researchers have demonstrated very complex models that arise in three or more species food chain models [34,35,36]. In marine ecosystem, much attention has been paid to top-down and down-top effects on plankton–fish dynamics [37,38,39,40,41]. But the combined study of a time delay with defense (i.e., phytoplankton uses toxicity and zooplankton uses DVM strategy) in plankton–fish interaction is still absent. A number of papers focused on effect of toxic and time delay on the dynamics of plankton system [42,43,44]. Saha and Bandyopadhyay [45] considered a phytoplankton–zooplankton model system with an additional term which represents extra morality of zooplankton due to toxicity of phytoplankton and studied the phenomenon of stability switching by choosing time delay as a bifurcation parameter. Sharma et al. [46] observed that the digestion time delay has the potential to destabilize the system dynamics in a plankton–fish interaction model. Pal and Chatterjee [47] have discussed the impact of time delay on stability behavior among phytoplankton, zooplankton and fish where the time delay is considered on planktivorous fish due to gestation delay. Liao et al. [48] studied a delayed phytoplankton–zooplankton interaction with Crowley–Martin functional response and revealed that delay can accelerate the procedure of its stability.

Recently, a number of developments have been addressed in the area of population dynamics focused on effect of time delay. Many scholars are excited about solving the system constituting with single or multiple time delays. Chen and Wang [18] investigated the impact of two different time delays on a prey–predator system with Monod–Haldane response function and showed the existence of Hopf bifurcation for possible combinations of two delays. Juneja et al. [27] studied a prey–predator system along with predator harvesting at different harvesting rates through time delay and found the prominent role of time delay in periodic oscillations. Liu and Jiang [37] studied a Gause-type predator–prey model with its biological implications and observed that time delay can switch stability and induced small amplitude oscillations. Time delay in the gestation of the predator is much effective than the feedback time delay of the prey [38]. Kumar et al. [52] explored the complex dynamics by incorporating time delay in the dissemination of information in a SIRS model and discussed its possible insight.

With this motivation, we consider three interacting components consisting of phytoplankton, zooplankton and planktivorous fish in our model system and incorporating discrete-time delay in the dynamics of zooplankton. The main objective of the current study is to closely observe the consequences of time delay on the plankton–fish interaction model where phytoplankton through the production of toxic substances and zooplankton through DVM exhibiting defense towards its predator and the structure of our paper is as follows: In Sect. 2, we have proposed a model system in which time delay is incorporated. Section 3 deals with the analytical methodologies for the proposed model system which includes the positivity and boundedness conditions, equilibria analysis, local stability analysis of positive equilibria and its transversality condition carried out by using its obtained characteristic equation, and at last global stability analysis followed by stability and direction of Hopf bifurcation. In Sect. 4, we have described numerical results to support our analytical findings. In Sect. 5, a discussion is presented for illustrating the biological relevance of our study. Finally, a conclusion is derived in the last section of the paper.

2 Model formulation

We consider a model for plankton–fish interaction with Monod–Haldane (MH)-type functional response. The model describes the interaction of prey, specialist predator and top specialist predator. At any time t, the phytoplankton x(t) is the favorite food of zooplankton y(t), which serves as favorite food for the fish z(t). We assume that the dynamics of the system arise from the coupling of interacting species where fish population z(t) depends only on zooplankton y(t) and zooplankton y(t) on plankton x(t). In the absence of a predator, the prey population grows logistic with carrying capacity K and intrinsic growth rate r. Interaction between (x, y) and (y, z) follows MH-type functional response which shows that phytoplankton and zooplankton both are equipped with defense mechanisms. The discrete-time delay has been incorporated in the model system. Under the above consideration, model system satisfies the following:

$$\begin{aligned} \begin{aligned} \frac{{\text {d}}x}{{\text {d}}t}&= rx \bigg (1-\frac{x}{K}\bigg )-\frac{c_1xy}{b_1x^2+m_1},\\ \frac{{\text {d}}y}{{\text {d}}t}&= -{\text {d}}_1y + \frac{e_1c_1x(t-\tau )y(t-\tau )}{b_1x^2(t-\tau )+m_1} -\frac{c_2yz}{b_2y^2+m_2},\\ \frac{{\text {d}}z}{{\text {d}}t}&= -{\text {d}}_2z+\frac{e_2c_2yz}{b_2y^2+m_2}. \end{aligned} \end{aligned}$$
(2.1)

The constant r and K represent the intrinsic growth rate and carrying capacity of prey, respectively. Different parameters used in the model represent different properties for prey and predators; that is, \(m_1\) and \(m_2\) are the half-saturation constant of prey and middle predator, \(b_1\) and \(b_2\) are the inverse measure of inhibitory effect of middle predator and top predator, \(c_1\) and \(c_2\) are the maximum value which can be attained by prey and middle predator for per capita reduction rate, \(d_1\) and \(d_2\) are the death rate of middle and top predator, and similarly, \(e_1\) and \(e_2\) are the conversion coefficient from individuals of prey to individuals of middle predator and individuals of middle predator to individuals of top predator, respectively.

Here the values of \(x,y,z,K,m_1\) and \(m_2\) are measured in number per unit area, values of \(r,c_1,c_2,d_1\) and \(d_2\) are measured in per day, and values of \(b_1\) and \(b_2\) are measured in per day\(^{-1}\).

The initial conditions of the system (2.1) are given as

$$\begin{aligned}&x(\theta ) =\phi _1(\theta ), y(\theta ) =\phi _2(\theta ), z(\theta ) =\phi _3(\theta ) \ \text {for all} ~\theta \in [-\tau ,0], \end{aligned}$$

where

$$\begin{aligned} (\phi _1,\phi _2,\phi _3)\in C([-\tau ,0],\mathfrak {R}_+^3), \ \phi _1(0),\phi _2(0),\phi _3(0) > 0. \end{aligned}$$

3 Analytical methodologies

3.1 Positive invariance and boundedness of the solutions

In this subsection, we demonstrate the positivity and boundedness conditions for the model system (2.1). For this purpose, we define the nonnegative cone by \(\mathfrak {R}_+^3=\{ (x, y, z)\in \mathfrak {R}_+^3 | x \ge 0;~ y \ge 0;~ z \ge 0\}\) and positive cone by int \((\mathfrak {R}_+^3)=\{ (x, y, z)\in \mathfrak {R}_+^3 | x> 0;~ y> 0;~ z > 0\}\).

Theorem 1

The positive cone for the system (2.1) with initial conditions is invariant.

Proof

To show the positivity condition, we have from the system (2.1),

$$\begin{aligned} x(t)&=x(0)\exp \Bigg \{\int _{0}^{t}\left( r \bigg (1-\frac{x(s)}{K}\bigg )-\frac{c_1y(s)}{b_1x^2(s)+m_1} \right) {\text {d}}s\Bigg \},\\ y(t)&=y(0)\exp \Bigg \{\int _{0}^{t}\left( -d_1 + \frac{e_1c_1x(s-\tau )y(s-\tau )}{y(s)(b_1x^2(s-\tau )+m_1)} \right.\\ &\left. \quad -\frac{c_2z(s)}{b_2y^2(s)+m_2}\right) {\text {d}}s\Bigg \},\\ z(t)&=z(0)\exp \Bigg \{\int _{0}^{t}\left(-d_2+\frac{e_2c_2y(s)}{b_2y^2(s)+m_2} \right) {\text {d}}s\Bigg \}, \end{aligned}$$

which shows that, \(x(t)>0\), \(y(t)>0\), \(z(t)>0\) if \(x(0)>0\), \(y(0)>0\), \(z(0)>0\). Therefore, the positive cone \(\mathfrak {R}_+^3\) is an invariant region. \(\square\)

Theorem 2

Let \(\Omega (t)=(x(t),y(t),z(t))\) be any positive solution of the system (2.1) , then there exists a \(T>0\) such that \(0 \le x(t) \le M\), \(0 \le y(t) \le M'\) and \(0 \le z(t) \le M''\), for \(t>T\), where

$$\begin{aligned} M&= K,\\ M'&= \frac{e_1rK}{4d_1},\\ M''&= e_2 \bigg ( \frac{e_1rK}{4b}-M' \bigg ). \end{aligned}$$

Proof

We already proved (x(t), y(t), z(t)) remains nonnegative in Theorem 1. So we only need to show that \(x(t) \le M\), \(y(t) \le M'\) and \(z(t) \le M''\).

From the first equation of the system (2.1), we have

$$\begin{aligned} \frac{{\text {d}}x}{{\text {d}}t} \le rx\bigg (1-\frac{x}{K}\bigg ),\ x(0)>0, \end{aligned}$$

thus, by simple calculation, we get

$$\begin{aligned} \lim \limits _{t\longrightarrow \infty } \sup x(t)\le K =M. \end{aligned}$$

Now we define a function

$$\begin{aligned} \chi (t) = x(t-\tau )+\frac{y(t)}{e_1}. \end{aligned}$$

Differentiating with respect to t, we get

$$\begin{aligned}&\frac{{\text {d}}\chi }{{\text {d}}t} =\frac{{\text {d}}x(t-\tau )}{{\text {d}}t}+\frac{1}{e_1} \frac{{\text {d}}y(t)}{{\text {d}}t},\\&\quad =rx(t-\tau )\bigg (1-\frac{x(t-\tau )}{K}\bigg )-\frac{c_1x(t-\tau )y(t-\tau )}{b_1x^2(t-\tau )+m_1}\\&\qquad -\frac{d_1}{e_1}y(t)+\frac{c_1x(t-\tau )y(t-\tau )}{b_1x^2(t-\tau )+m_1}\\&\qquad -\frac{c_2y(t)z(t)}{e_1(b_2y^2(t)+m_2)},\\&\frac{{\text {d}}\chi }{{\text {d}}t} \le rx(t-\tau )\bigg (1-\frac{x(t-\tau )}{K}\bigg )-\frac{d_1}{e_1}y(t)-d_1x(t-\tau )\\&\qquad +d_1x(t-\tau ),\\&\frac{{\text {d}}\chi }{{\text {d}}t} +d_1\chi (t) \le \frac{rK}{4}+d_1K, \ {\text {since,}} \ \max x\bigg (1-\frac{x}{K}\bigg ) =\frac{K}{4}. \end{aligned}$$

By comparison lemma for \(t \ge {\tilde{T}} \ge 0\), we obtain

$$\begin{aligned} \chi (t) \le \frac{rK}{4d_1}+K-\bigg ( \frac{rK}{4d_1}+K-\chi ({\tilde{T}}) \bigg ) {\text {e}}^{-d_1(t-{\tilde{T}})}, \end{aligned}$$

If \({\tilde{T}}=0\), then

$$\begin{aligned} \chi (t) \le \frac{rK}{4d_1}+K-\bigg ( \frac{rK}{4d_1}+K-\chi (0) \bigg ) {\text {e}}^{-d_1t}. \end{aligned}$$

For the large value of t, we have

$$\begin{aligned} x(t-\tau )+\frac{y(t)}{e_1}&\le \frac{rK}{4d_1}+K,\\ \frac{y(t)}{e_1}&\le \frac{rK}{4d_1}. \end{aligned}$$

Therefore,

$$\begin{aligned} y(t)\le \frac{e_1rK}{4d_1}=M'. \end{aligned}$$

Again, we define a function

$$\begin{aligned} \rho (t) = e_1x(t-\tau )+y(t)+\frac{z(t)}{e_2}. \end{aligned}$$

Differentiating with respect to t, we get

$$\begin{aligned} \frac{{\text{d}}\rho }{{\text{d}}t}&=e_1\frac{{\text{d}}x(t-\tau )}{{\text{d}}t}+\frac{dy(t)}{{\text{d}}t}+\frac{1}{e_2} \frac{{\text{d}}z(t)}{{\text{d}}t},\\&=e_1rx(t-\tau )\bigg (1-\frac{x(t-\tau )}{K}\bigg )\\&\quad -\frac{e_1c_1x(t-\tau )y(t-\tau )}{b_1x^2(t-\tau )+m_1}-d_1y(t)+\frac{e_1c_1x(t-\tau )y(t-\tau )}{b_1x^2(t-\tau )+m_1}\\&\quad -\frac{c_2y(t)z(t)}{b_2y^2(t)+m_2}-\frac{d_2}{e_2}z(t)+\frac{c_2y(t)z(t)}{b_2y^2(t)+m_2},\\ \frac{{\text{d}}\rho }{{\text{d}}t}&=e_1rx(t-\tau )\bigg (1-\frac{x(t-\tau )}{K}\bigg )-d_1y(t)-\frac{d_2}{e_2}z(t),\\ \frac{{\text{d}}\rho }{{\text{d}}t}&\le \frac{e_1rK}{4}-d_1y(t)-\frac{d_2}{e_2}z(t), \ \text {since,} \ \max x\bigg (1-\frac{x}{K}\bigg )=\frac{K}{4}. \end{aligned}$$

Taking \(b=\min \{d_1,d_2\}\), which implies

$$\begin{aligned} \frac{{\text{d}}\rho }{{\text{d}}t}&\le \frac{e_1rK}{4}-b\bigg (y(t)+\frac{z(t)}{e_2}\bigg )-be_1x(t-\tau )+be_1x(t-\tau ),\\ \frac{{\text{d}}\rho }{{\text{d}}t}&+b\rho \le \frac{e_1rK}{4}+be_1K. \end{aligned}$$

By comparison lemma for \(t \ge {\tilde{T}} \ge 0\), we obtain

$$\begin{aligned} \rho \le \frac{e_1rK}{4b}+e_1K-\bigg (\frac{e_1rK}{4b}+e_1K-\rho ({\tilde{T}}) \bigg ) {\text {e}}^{-b(t-{\tilde{T}})}, \end{aligned}$$

If \({\tilde{T}}=0\), then

$$\begin{aligned} \rho \le \frac{e_1rK}{4b}+e_1K-\bigg (\frac{e_1rK}{4b}+e_1K-\rho (0) \bigg ) {\text {e}}^{-bt}, \end{aligned}$$

For the large value of t, we have

$$\begin{aligned} e_1x(t-\tau )+y(t)+\frac{z(t)}{e_2}&\le \frac{e_1rK}{4b}+e_1K,\\ y(t)+\frac{z(t)}{e_2}&\le \frac{e_1rK}{4b}. \end{aligned}$$

Therefore,

$$\begin{aligned} z(t) \le e_2 \bigg ( \frac{e_1rK}{4b}-M' \bigg )=M'' \ \text {such that} \ e_1rK>4b M'. \end{aligned}$$

Thus all species are uniformly bounded for initial value in \(\mathfrak {R}_+^3\). This completes the proof of Theorem 2. \(\square\)

3.2 Equilibrium analysis

In this subsection, the existence of possible equilibria and stability condition corresponding to the different equilibrium points is investigated. It is clear that model system (2.1) possesses four nonnegative equilibrium points, namely \(E_0(0,0,0)\), \(E_x(K,0,0)\), \(E_{xy}(x_3,y_3,0)\) and \(E^*(x^*,y^*,z^*)\).

  1. (i)

    Existence of \(E_0(0,0,0)\) as trivial equilibrium point. The eigenvalues of the variational matrix around \(E_0\) are r, \(-d_1\) and \(-d_2\). The variational matrix has a positive root and two negative roots. Hence, \(E_0\) is a is saddle point with two-dimensional stable manifold in yz-plane and one-dimensional unstable manifold in x-direction.

  2. (ii)

    Existence of \(E_x(K,0,0)\) as predator free equilibrium point. The eigenvalues of the variational matrix around \(E_x\) are \(-r\), \(-d_1+\frac{e_1c_1K}{b_1K^2+m_1}\) and \(-d_2\). The variational matrix has two negative roots. Hence, \(E_x\) is also a saddle point with two-dimensional stable manifold in xz-plane and one-dimensional unstable manifold in y-direction if \(e_1c_1K>d_1(b_1K^2+m_1)\). \(E_x\) is locally asymptotically stable, if \(e_1c_1K<d_1(b_1K^2+m_1)\).

  3. (iii)

    Existence of \(E_{xy}(x_3,y_3,0)\) as top-predator free equilibrium point, where \(x_3\) and \(y_3\) are obtained by the following relations;

    $$\begin{aligned}&x_3 =\frac{\frac{e_1c_1}{b_1d_1}\pm \sqrt{\big (\frac{e_1c_1}{b_1d_1}\big )^2-\frac{4m_1}{b_1}}}{2},\\&y_3 =\frac{r}{c_1}\bigg ( 1-\frac{x_3}{K} \bigg )(b_1x^{2}_{3}+m_1). \end{aligned}$$

    If \(\big (\frac{e_1c_1}{b_1d_1}\big )^2\ge \frac{4m_1}{b_1}\) then \(E_{xy}\) is positive and real, provided \(K>x_3\). The variational matrix around \(E_{xy}\) satisfies the following:

    $$\begin{aligned} \lambda _1+\lambda _2&=-\frac{rx_3}{K}+\frac{2b_1c_1x_3^2y_3}{(b_1x^2_3+m_1)^2}, \\ \lambda _1\lambda _2&=\frac{(m_1-b_1x_3^2)e_1c_1^2x_3y_3}{(b_1x_3^2+m_1)^2}, \\ \lambda _3&= -d_2+\frac{e_2c_2y_3}{b_2y_3^2+m_2}. \end{aligned}$$

    Two eigenvalues \(\lambda _1\) and \(\lambda _2\) have negative real parts if \(\lambda _1+\lambda _2<0\) and \(\lambda _1\lambda _2>0\). Hence, the equilibrium point \(E_{xy}\) is locally asymptotically stable, if \(\frac{rx_3}{K}>\frac{2b_1c_1x_3^2y_3}{(b_1x^2_3+m_1)^2}\), \(m_1-b_1x_3^2>0\) and \(\frac{e_2c_2y_3}{b_2y_3^2+m_2}>d_2\) holds.

  4. (iv)

    Existence of coexistence equilibrium point \(E^*(x^*,y^*,z^*)\), where \(x^*\) is the positive root of the following equation

    $$\begin{aligned} x^{*3}-Kx^{*2}+\frac{m_1}{b_1}x^*+\frac{K}{b_1}\bigg ( \frac{c_1y^*}{r}-m_1 \bigg )=0. \end{aligned}$$
    (3.1)

    Let \(f(x^*)=x^{*3}-Kx^{*2}+\frac{m_1}{b_1}x^*+\frac{K}{b_1}\bigg ( \frac{c_1y^*}{r}-m_1 \bigg )\), then \(f(0)=\frac{K}{b_1}\bigg ( \frac{c_1y^*}{r}-m_1 \bigg )\), \(f(0)<0\) if \(y^*<\frac{m_1r}{c_1}\) and \(f(K)=\frac{c_1Ky^*}{rb_1}>0\). Since \(f(0)f(K)<0\), by intermediate value theorem, Eq. (3.1) has a positive root lies in (0, K) when

    $$\begin{aligned} y^*<\frac{m_1r}{c_1}. \end{aligned}$$
    (3.2)

    \(y^*\) is a positive root of the quadratic equation

    $$\begin{aligned} g(y^*) = y^*-\frac{e_2c_2}{b_2d_2}y^*+\frac{m_2}{b_2}=0. \end{aligned}$$
    (3.3)

    Roots of \(g(y^*) = 0\) take the form \(y^* =\frac{\frac{e_2c_2}{b_2d_2}\pm \sqrt{\big (\frac{e_2c_2}{b_2d_2}\big )^2-\frac{4m_2}{b_2}}}{2}\), out of which at least one will be positive provided one of the following conditions holds:

    $$\begin{aligned} \begin{aligned}&\text {(a)} \ \frac{e_2c_2}{b_2d_2}>0 \ \text {and} \ \frac{m_2}{b_2}<0,\\&\text {(b)} \ \frac{e_2c_2}{b_2d_2}>0, \frac{m_2}{b_2}>0 \ \text {and} \ \bigg (\frac{e_2c_2}{b_2d_2}\bigg )^2-\frac{4m_2}{b_2}>0,\\&\text {(c)} \ \frac{e_2c_2}{b_2d_2}<0 \ \text {and} \ \frac{m_2}{b_2}<0. \end{aligned} \end{aligned}$$
    (3.4)

    \(z^*\) is given by the equation

    $$\begin{aligned} z^*=\frac{1}{c_2}\bigg (-d_1+\frac{e_1c_1x^*}{b_1x^{*2}+m_1}\bigg ) (b_2y^{*2}+m_2), \end{aligned}$$
    (3.5)

    where \(z^*>0\) if

    $$\begin{aligned} d_1<\frac{e_1c_1x^*}{b_1x^{*2}+m_1}. \end{aligned}$$
    (3.6)

    Hence, the coexistence equilibrium \(E^*(x^*,y^*,z^*)\) exists if the conditions (3.2), (3.4) and (3.6) hold.

3.3 Local stability analysis about \(E^*(x^*,y^*,z^*)\)

Now we focus on the study of local stability around the positive equilibria \(E^*(x^*,y^*,z^*)\) and occurrence of Hopf bifurcation of the system (2.1). For this, let \(x(t)=x^*+X(t)\), \(y(t)=y^*+Y(t)\) and \(z(t)=z^*+Z(t)\). This helps to perturb the system (2.1) and we get a new system of equations as follows:

$$\begin{aligned} \frac{d}{{\text{d}}t}\left( \begin{array}{c} X(t) \\ Y(t) \\ Z(t) \end{array}\right) =J\left( \begin{array}{c} X(t) \\ Y(t) \\ Z(t) \end{array}\right) +J'\left( \begin{array}{c} X(t-\tau ) \\ Y(t-\tau ) \\ Z(t-\tau ) \end{array}\right) , \end{aligned}$$
(3.7)

where

$$\begin{aligned} J=\left( \begin{array}{ccc} a &{} b &{} 0 \\ 0 &{} c &{} d \\ 0 &{} e &{} 0 \end{array}\right) \quad and \quad J'=\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ f &{} g &{} 0 \\ 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

in which

$$\begin{aligned} a&= -\frac{rx^*}{K}+\frac{2b_1c_1x^{*2}y^*}{(b_1x^{*2}+m_1)^2},\\ b&= -\frac{c_1x^*}{b_1x^{*2}+m_1},\\ c&= -d_1-\frac{(m_2-b_2y^{*2})c_2z^*}{(b_2y^{*2}+m_2)^2},\\ d&= -\frac{c_2y^*}{b_2y^{*2}+m_2},\\ e&= \frac{(m_2-b_2y^{*2})e_2c_2z^*}{(b_2y^{*2}+m_2)^2},\\ f&= \frac{(m_1-b_1x^{*2})e_1c_1y^*}{(b_1x^{*2}+m_1)^2},\\ g&= \frac{e_1c_1x^*}{b_1x^{*2}+m_1}. \end{aligned}$$

The characteristic equation of the delayed system (2.1) takes the form

$$\begin{aligned}&\lambda ^3+A\lambda ^2+B\lambda +C+{\text {e}}^{-\lambda \tau }(D\lambda ^2\nonumber +E\lambda )=0, \end{aligned}$$
(3.8)

where

$$\begin{aligned} A&=-(a+c), \\ B&=ac-de, \\ C&=ade, \\ D&=-g,\\ E&=ag-bf. \end{aligned}$$

When \(\tau =0\), we get the characteristic equation of delay free system, which is given by

$$\begin{aligned} \lambda ^3+(A+D)\lambda ^2+(B+E)\lambda +C=0. \end{aligned}$$
(3.9)

Therefore, the stability conditions for \(E^*(x^*,y^*,z^*)\) are defined by the following hypothesis;

Hypothesis (\(\varvec{H}_{{\mathbf{1}}}\))

$$\begin{aligned} {(A+D)>0, C>0,} \end{aligned}$$

Hypothesis (\(\varvec{H}_{{\mathbf{2}}}\))

$$\begin{aligned} (A+D)(B+E)-C>0. \end{aligned}$$

Then, by Routh–Hurwitz criterion, we state that:

Lemma 1

If Hypotheses (\(H_1\)) and (\(H_2\)) hold, then all the roots of Eq. (3.9) have negative real parts which show that the coexistence equilibrium \(E^*(x^*,y^*,z^*)\) is locally asymptotically stable for \(\tau =0\).

For occurrence of Hopf bifurcation, it can be assumed that Eq. (3.8) has a pair of purely imaginary roots. Let this root be \(\lambda = i\omega _0\), \(\tau =\tau _0\) and putting this into Eq. (3.8), for simplicity, referring \(\omega _0\) and \(\tau _0\) by \(\omega ,\tau\), respectively, we obtained

$$\begin{aligned} \begin{aligned}&-i\omega ^3-A\omega ^2+iB\omega +C-D\omega ^2\cos \omega \tau +iE\omega \cos \omega \tau \\&\quad +iD\omega ^2\sin \omega \tau +E\omega \sin \omega \tau =0. \end{aligned} \end{aligned}$$
(3.10)

Separating the real and imaginary parts, we have

$$\begin{aligned} -A\omega ^2+C=D\omega ^2\cos \omega \tau -E\omega \sin \omega \tau , \end{aligned}$$
(3.11)
$$\begin{aligned} -\omega ^3+B\omega =-E\omega \cos \omega \tau -D\omega ^2\sin \omega \tau . \end{aligned}$$
(3.12)

Now, squaring and adding leads the following six-degree equation;

$$\begin{aligned} \begin{aligned} \omega ^6+(A^2-2B-D^2)\omega ^4+(B^2-2AC-E^2)\omega ^2+C^2=0. \end{aligned} \end{aligned}$$
(3.13)

By simple algebraic calculation and taking \(u=\omega ^2\), Eq. (3.13) becomes

$$\begin{aligned} u^3+Q_1u^2+Q_2u+Q_3=0, \end{aligned}$$
(3.14)

where

$$\begin{aligned} Q_1&=(A^2-2B-D^2),\\ Q_2&=(B^2-2AC-E^2),\\ Q_3&=C^2. \end{aligned}$$

For the roots distribution, let

$$\begin{aligned} H(u)=u^3+Q_1u^2+Q_2u+Q_3, \end{aligned}$$
(3.15)

then

$$\begin{aligned} H'(u)=3u^2+2Q_1u+Q_2. \end{aligned}$$
(3.16)

Hence, \(H'(u)=0\) has two roots, which are given by

$$\begin{aligned} u_{1}^{*}&=\frac{-Q_1+\sqrt{(Q_1^2-3Q_2)}}{3},\\ u_{2}^{*}&=\frac{-Q_1-\sqrt{(Q_1^2-3Q_2)}}{3}. \end{aligned}$$

Now, we make the hypothesis which is given below;

Hypothesis (\(\varvec{H}_{{\mathbf{3}}}\))

$$\begin{aligned} u_{1}^{*}>0, \ H(u_{1}^{*})<0, \ {Q_1^2-3Q_2\geqslant 0}. \end{aligned}$$

Since \(Q_3>0\), Eq. (3.14) has no real positive roots if \(Q_1-3Q_2<0\) (see lemma 2.1 in [49]) and two real positive roots if Hypothesis (\(H_3\)) holds and these roots be \(\omega _j(j=1,2)\). Let \(\omega _1<\omega _2\) then \(H'(\omega _1)<0\) and \(H'(\omega _2)>0\) (see lemma 3.2 in [50]).

By Eqs. (3.11) and (3.12), we obtained following equation,

$$\begin{aligned} \cos \omega \tau = \frac{(E-AD)\omega ^2+(CD-BE)}{D^2\omega ^2+E^2}. \end{aligned}$$
(3.17)

The critical value of time delay is given by

$$\begin{aligned} \tau ^{k}_{j}= \frac{1}{\omega _j}\bigg [ \arccos \bigg \{ \frac{(E-AD)\omega ^{2}_{j}+(CD-BE)}{D^2\omega ^{2}_{j}+E^2} \bigg \} +2k\pi \bigg ], \end{aligned}$$
(3.18)

where j = 1, 2, k = 0, 1, 2,...

Lemma 2

If Hypothesis (\(H_3\)) holds, then Eq. (3.8) has a pair of pure imaginary roots \(\pm i\omega _j\) and all other roots have nonzero real parts at \(\tau =\tau _j^k(j=1,2,k=0,1,2,\ldots )\).

In addition, we define \(\tau _0 = \min _{j=1, 2}\{ \tau _j^0 \}\), i.e., \(\tau _0\) represents the smallest positive value of \(\tau _{j}^{0}, j=1,2\) given by Eq. (3.18) and \(\omega _0=\omega _{j_0}\).

Lemma 3

If Hypothesis (\(H_3\)) holds, then we have the following two transversality conditions:

\({ sign}\bigg \{\frac{{\text {d}}\mathfrak {R}\lambda (\tau )}{{\text {d}}\tau }\bigg \}_{\tau =\tau _{1}^{k}}<0\)  and  \({ sign}\bigg \{\frac{{\text {d}}\mathfrak {R}\lambda (\tau )}{{\text {d}}\tau }\bigg \}_{\tau =\tau _{2}^{k}}>0\),  where k=0,1,2...

Proof

Differentiating Eq. (3.8) w.r.t. \(\tau\), we obtained

$$\begin{aligned} \bigg ( \frac{{\text{d}}\lambda }{{\text{d}}\tau } \bigg )^{-1}=\frac{(3\lambda ^2+2A\lambda +B){\text {e}}^{\lambda \tau }}{\lambda (D\lambda ^2+E\lambda )}+\frac{(2D\lambda +E)}{\lambda (D\lambda ^2+E\lambda )}- \frac{\tau }{\lambda }. \end{aligned}$$

Then,

$$\begin{aligned} \bigg [ \mathfrak {R}\bigg ( \frac{{\text{d}}\lambda }{{\text{d}}\tau } \bigg )^{-1} \bigg ]_{\tau =\tau _j} = \frac{H'(\omega ^{2}_{j})}{V_j\omega ^{2}_{j}}, \end{aligned}$$

where

$$\begin{aligned} V_j= D^2\omega ^{2}_{j}+E^2, \end{aligned}$$

where j = 1, 2.

Therefore, the required transversality condition is obtained if \(H'(\omega ^{2}_{1})<0\) and \(H'(\omega ^{2}_{2})>0\). \(\square\)

3.4 Global stability analysis about \(E^*(x^*,y^*,z^*)\)

For global stability analysis, we have following theorem:

Theorem 3

If \(\min {\alpha _1,\alpha _2,\alpha _3}>0\), with

$$\begin{aligned} \begin{aligned} \alpha _1&=\Bigg \{\bigg (\frac{r}{K}-\frac{c_1y^*}{mb_1x^{*2}}-\frac{c_1y^*}{m_1x^*}\bigg )-\frac{2e_1c_1y^*}{m'b_1x^*}\bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )\Bigg \},\\ \alpha _2&=\Bigg \{\frac{c_1}{m_1}+\frac{e_1c_1}{M'b_1x^*}-\frac{c_2z^*}{m'b_2y^{*2}}-\frac{c_2z^*}{m_2y^*}-\frac{e_1c_1}{m'b_1x^*}\\&\quad -\frac{e_1c_1M'\tau }{m'b_1x^*y^*}\bigg (\frac{e_1c_1y^*}{M'b_1x^*}+\frac{c_2z^*}{m'b_2y^*}+\frac{c_2z^*}{m_2}\bigg )-\frac{2e_2c_2z^*}{m''b_2y^{*2}}\Bigg \},\\ \alpha _3&=\Bigg \{-\frac{c_2}{m_2}\bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )+\frac{e_2c_2}{M''b_2y^*}-\frac{e_2c_2}{m''b_2y^*}\Bigg \}, \end{aligned} \end{aligned}$$

where \(m<x(t)<M,m'<y(t)<M'\) and \(m''<z(t)<M''\) for \(t>0\), then the interior equilibrium \(E^*\) of the model system (2.1) is globally asymptotically stable.

Proof

A suitable Lyapunov function is constructed for proving the theorem. This function should guarantee the global stability of the positive interior of equilibrium \(E^*(x^*,y^*,z^*)\) for system model (2.1). We transform the variables by using the following substitutions:

$$\begin{aligned} x=x^*{\text {e}}^{X(t)}, \quad y=y^*{\text {e}}^{Y(t)}, \quad z=z^*{\text {e}}^{Z(t)}. \end{aligned}$$
(3.19)

The interior equilibrium \(E^*\) for trivial equilibrium condition \(X(t),Y(t),Z(t)=0\) for all value of \(t>0\) is transformed by the above-mentioned coordinates. Reduced model system (2.1) is as follows:

$$\begin{aligned}&\begin{aligned} \frac{{\text{d}}X}{{\text{d}}t} =&{} -\frac{rx^*}{K}({\text {e}}^{X(t)}-1)\\&-\frac{c_1y^*(b_1x^{*2}+m_1)}{(b_1x^{2}+m_1)(b_1x^{*2}+m_1)}({\text {e}}^{Y(t)}-1)\\&+\frac{b_1c_1xy^*x^*}{(b_1x^{2}+m_1)(b_1x^{*2}+m_1)}({\text {e}}^{X(t)}-1)\\&+\frac{b_1c_1x^{*2}y^*}{(b_1x^{2}+m_1)(b_1x^{*2}+m_1)}({\text {e}}^{X(t)}-1), \end{aligned} \end{aligned}$$
(3.20)
$$\begin{aligned}&\begin{aligned} \frac{{\text{d}}Y}{{\text{d}}t} =&{} -\frac{e_1c_1x^*y^*}{y(b_1x^{*2}+m_1)}({\text {e}}^{Y(t)}-1)\\&+\frac{e_1c_1x(t-\tau )y^*}{y(b_1x^2(t-\tau )+m_1)}({\text {e}}^{Y(t-\tau )}-1)\\&+\frac{e_1c_1x^*y^*(m_1-b_1x^*x(t-\tau ))}{y(b_1x^{*2}+m_1)(b_1x^2(t-\tau )+m_1)}\\&\times ({\text {e}}^{X(t-\tau )}-1) \\&+\frac{b_2c_2yy^*z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}({\text {e}}^{Y(t)}-1) \\&+\frac{b_2c_2y^{*2}z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}({\text {e}}^{Y(t)}-1)\\&-\frac{c_2z^*(b_2y^{*2}+m_2)}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)} ({\text {e}}^{Z(t)}-1), \end{aligned} \end{aligned}$$
(3.21)
$$\begin{aligned}&\begin{aligned} \frac{{\text{d}}Z}{{\text{d}}t} =&{} -\frac{e_2c_2y^*z^*}{z(b_2y^{*2}+m_2)}({\text {e}}^{Z(t)}-1)\\&+\frac{e_2c_2yz^*(b_2y^{*2}+m_2)}{z(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}({\text {e}}^{Z(t)}-1)\\&+\frac{e_2c_2y^*z^*(m_2-b_2yy^*)}{z(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}\\&\times ({\text {e}}^{Y(t)}-1). \end{aligned} \end{aligned}$$
(3.22)

Let \(V_1(t)=|X(t)|\). Evaluating the upper right derivative of \(V_1(t)\) along the obtained results of (2.1), we get

$$\begin{aligned} \begin{aligned} D^+V_1(t) \le&-\frac{rx^*}{K}|{\text {e}}^{X(t)}-1|\\&-\frac{c_1y^*}{(b_1x^{2}+m_1)}|{\text {e}}^{Y(t)}-1| \\&+\frac{b_1c_1xy^*x^*}{(b_1x^{2}+m_1)(b_1x^{*2}+m_1)}|{\text {e}}^{X(t)}-1|\\&+\frac{b_1c_1x^{*2}y^*}{(b_1x^{2}+m_1)(b_1x^{*2}+m_1)}|{\text {e}}^{X(t)}-1|,\\ \le&-\frac{rx^*}{K}|{\text {e}}^{X(t)}-1|-\frac{c_1y^*}{m_1} |{\text {e}}^{Y(t)}-1|\\&+\frac{c_1y^*}{mb_1x^*}|{\text {e}}^{X(t)}-1|+\frac{c_1y^*}{m_1} |{\text {e}}^{X(t)}-1|\\ =&-\bigg (\frac{rx^*}{K}-\frac{c_1y^*}{mb_1x^*}-\frac{c_1y^*}{m_1}\bigg ) |{\text {e}}^{X(t)}-1|\\&-\frac{c_1y^*}{m_1}|{\text {e}}^{Y(t)}-1|. \end{aligned} \end{aligned}$$
(3.23)

Now, Eq.(3.21) can be rewritten as

$$\begin{aligned} \begin{aligned} \frac{{\text{d}}Y}{{\text{d}}t} ={}& \,-\frac{e_1c_1x^*y^*}{y(b_1x^{*2}+m_1)}({\text {e}}^{Y(t)}-1)\\&+ \frac{e_1c_1x^*y^*(m_1-b_1x^*x(t-\tau ))}{y(b_1x^{*2}+m_1)(b_1x^2(t-\tau )+m_1)}({\text {e}}^{X(t-\tau )}-1)\\&+\frac{b_2c_2yy^*z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}({\text {e}}^{Y(t)}-1)\\&+ \frac{b_2c_2y^{*2}z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}({\text {e}}^{Y(t)}-1)\\&-\frac{c_2z^*(b_2y^{*2}+m_2)}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)} ({\text {e}}^{Z(t)}-1) \\&+\frac{e_1c_1x(t-\tau )y^*}{y(b_1x^2(t-\tau )+m_1)}({\text {e}}^{Y(t)}-1)\\&-\frac{e_1c_1x(t-\tau )y^*}{y(b_1x^2(t-\tau )+m_1)}\\&\int _{t-\tau }^{t} {\text {e}}^{Y(s)} \Bigg \{-\frac{e_1c_1x^*y^*}{y(b_1x^{*2}+m_1)}({\text {e}}^{Y(s)}-1)\\&+\frac{e_1c_1x^*y^*(m_1-b_1x^*x(t-\tau ))}{y(b_1x^{*2}+m_1)(b_1x^2(t-\tau )+m_1)}({\text {e}}^{X(s-\tau )}-1)\\&+\frac{b_2c_2yy^*z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}\\&\times ({\text {e}}^{Y(s)}-1)+\frac{b_2c_2y^{*2}z^*}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)} ({\text {e}}^{Y(s)}-1)\\&-\frac{c_2z^*(b_2y^{*2}+m_2)}{(b_2y^{2}+m_2)(b_2y^{*2}+m_2)}\\&\times ({\text {e}}^{Z(s)}-1) +\frac{e_1c_1x(t-\tau )y^*}{y(b_1x^2(t-\tau )+m_1)} ({\text {e}}^{Y(s-\tau )}-1)\Bigg \}{\text {d}}s. \end{aligned} \end{aligned}$$
(3.24)

In the above equation, we use the following relation

$$\begin{aligned} {\text {e}}^{Y(t-\tau )}={\text {e}}^{Y(t)}-\int _{t-\tau }^{t} {\text {e}}^{Y(s)}\frac{{\text{d}}Y}{{\text {d}}s}{\text {d}}s. \end{aligned}$$
(3.25)

Let \(V_2(t)=|Y(t)|\). Evaluating the upper right derivative of \(V_2(t)\) along the obtained results of (2.1), following from Eq. (3.21), we get

$$\begin{aligned} \begin{aligned} D^+V_2(t)&\le -\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(t)}-1|+\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(t-\tau )}-1|\\&+\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(t)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(t)}-1|\\&+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(t)}-1|+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(t)}\\&-1|+\frac{e_1c_1y^*}{m'b_1x^*}\int _{t-\tau }^{t} {\text{e}}^{Y(s)} \Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(s)}-1|\\&+\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(s-\tau )}-1|+\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(s)}-1|\\&+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(s)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(s)}-1|\\&+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(s-\tau )}-1|\Bigg \}. \end{aligned} \end{aligned}$$
(3.26)

We find that there exists a \(T>0\), such that \(y^*{\text{e}}^{Y(t)}<M'\) for all \(t>T\), and for \(t>T+\tau\), we get

$$\begin{aligned} \begin{aligned} D^+V_2(t) \le&-\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(t)}-1|+\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(t-\tau )}-1|\\&+\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(t)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(t)}-1|\\&+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(t)}-1|+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(t)}-1| \\&+\frac{e_1c_1M'}{m'b_1x^*}\int _{t-\tau }^{t} \Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(s)}-1|\\&+\frac{2e_1c_1y^*}{m'b_1x^*}\\&\times |{\text{e}}^{X(s-\tau )}-1| +\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(s)}-1| \\&+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(s)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(s)}-1|\\&+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(s-\tau )}-1|\Bigg \}{\text {d}}s. \end{aligned} \end{aligned}$$
(3.27)

Again due to structure of (3.27), we consider the following functional

$$\begin{aligned} \begin{aligned} V_{22}(t) =&V_2(t)+\frac{e_1c_1M'}{m'b_1x^*}\int _{t-\tau }^{t}\int _{Y}^{t}\Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(s)}-1|\\&+\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(s-\tau )}-1|\\&+\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(s)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(s)}-1|\\&+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(s)}-1|+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(s-\tau )}-1|\Bigg \}dsdY\\&+\frac{2e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}\int _{t-\tau }^{t}|{\text{e}}^{X(s)}-1|{\text {d}}s\\&+\frac{e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}\int _{t-\tau }^{t}|{\text{e}}^{Y(s)}-1|{\text {d}}s\\&+\frac{2e_1c_1y^*}{m'b_1x^*}\int _{t-\tau }^{t}|{\text{e}}^{X(s)}-1|{\text {d}}s, \end{aligned} \end{aligned}$$
(3.28)

whose upper right derivative along the solutions of the system (2.1) is given by

$$\begin{aligned}&D^+V_{22}(t) \\&\quad = D^+V_2+\frac{e_1c_1M'\tau }{m'b_1x^*}\Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(t)}-1|\\&\qquad +\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(t-\tau )}-1|+\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(t)}-1|\\&\qquad +\frac{c_2z^*}{m_2}|{\text{e}}^{Y(t)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Z(t)}-1|\\&\qquad +\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(t-\tau )}-1|\Bigg \}-\frac{e_1c_1M'}{m'b_1x^*}\\&\qquad \times \int _{t-\tau }^{t}\Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(s)}-1| +\frac{2e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{X(s-\tau )}-1|\\&\qquad +\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(s)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(s)}-1|\\&\qquad +\frac{c_2z^*}{m_2}|{\text{e}}^{Z(s)}-1|+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(s-\tau )}-1|\Bigg \}\\&\qquad +\frac{e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}[|{\text{e}}^{X(t)}-1|-|{\text{e}}^{X(t-\tau )}-1|]\\&\qquad +\Bigg \{\frac{e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}[|{\text{e}}^{X(t)}-1|-|{\text{e}}^{Y(t)}-1|]\\&\qquad -\frac{e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}[|{\text{e}}^{X(t-\tau )}-1|-|{\text{e}}^{Y(t-\tau )}-1|]\Bigg \}\\&\qquad +\frac{2e_1c_1y^*}{m'b_1x^*}[|{\text{e}}^{X(t)}-1|-|{\text{e}}^{X(t-\tau )}-1|], \end{aligned}$$

which implies

$$\begin{aligned} \begin{aligned}&D^+V_{22}(t)\\&\quad \le -\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(t)}-1| +\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(t)-1}|\\&\qquad +\frac{c_2z^*}{m_2}|{\text{e}}^{Y(t)}-1|+\frac{e_1c_1y^*}{m'b_1x^*}|{\text{e}}^{Y(t)}-1|\\&\qquad +\frac{c_2z^*}{m_2}|{\text{e}}^{Z(t)}-1| +\frac{e_1c_1M'\tau }{m'b_1x^*}\Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}|{\text{e}}^{Y(t)}-1|\\&\qquad +\frac{c_2z^*}{m'b_2y^*}|{\text{e}}^{Y(t)}-1|+\frac{c_2z^*}{m_2}|{\text{e}}^{Y(t)}-1|\\&\qquad +\frac{c_2z^*}{m_2}|{\text{e}}^{Z(t)}-1|\Bigg \}+\frac{2e_1^2c_1^2M'y^*\tau }{m'^2b_1^2x^{*2}}|{\text{e}}^{X(t)}-1|\\&\quad =\frac{2e_1c_1y^*}{m'b_1x^*}\Bigg (1 +\frac{e_1c_1M'\tau }{m'b_1x^*}\Bigg )|{\text{e}}^{X(t)}-1|\\&\qquad +\Bigg [-\frac{e_1c_1y^*}{M'b_1x^*}+\frac{c_2z^*}{m'b_2y^*}\\&\qquad +\frac{c_2z^*}{m_2}+\frac{e_1c_1y^*}{m'b_1x^*}+\frac{e_1c_1M'\tau }{m'b_1x^*}\Bigg \{\frac{e_1c_1y^*}{M'b_1x^*}+\frac{c_2z^*}{m'b_2y^*}\\&\qquad +\frac{c_2z^*}{m_2}\Bigg \}\Bigg ]+\frac{c_2z^*}{m_2}\Bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\Bigg )|{\text{e}}^{Z(1)}-1|. \end{aligned} \end{aligned}$$
(3.29)

Again, Let \(V_3(t)=|Z(t)|\). Evaluating the upper right derivative of \(V_3(t)\) along the obtained results of (2.1), we get

$$\begin{aligned} \begin{aligned} D^+V_3(t)&\le -\frac{e_2c_2z^*}{b_2y^*z}|{\text{e}}^{Z(t)}-1|+\frac{e_2c_2z^*}{b_2y^*z}|{\text{e}}^{Z(t)}-1|\\&\quad +\frac{2e_2c_2z^*}{b_2y^*z}|{\text{e}}^{Y(t)}-1|\\&\le -\frac{e_2c_2z^*}{b_2y^*M''}|{\text{e}}^{Z(t)}-1|+\frac{e_2c_2z^*}{b_2y^*m''}|{\text{e}}^{Z(t)}-1|\\&\quad +\frac{2e_2c_2z^*}{b_2y^*m''}|{\text{e}}^{Y(t)}-1|. \end{aligned} \end{aligned}$$
(3.30)

We define a Lyapunov functional V(t) as

$$\begin{aligned} V(t)=V_1(t)+V_{22}(t)+V_3(t)>|X(t)|+|Y(t)|+|Z(t)|. \end{aligned}$$
(3.31)

Evaluating the upper right derivative of V(t) along the obtained results of system (2.1), and by using Eqs. (3.23), (3.29) and (3.30), we get

$$\begin{aligned} \begin{aligned}&D^+V(t) \\&\quad =D^+V_1(t)+D^+V_{22}(t)+D^+V_3(t)\\&\quad \le \Bigg \{-\bigg (\frac{r}{K}-\frac{c_1y^*}{mb_1x^{*2}} -\frac{c_1y^*}{m_1x^*}\bigg ) \\&\qquad +\frac{2e_1c_1y^*}{m'b_1x^*} \bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )\Bigg \}|{\text{e}}^{X(t)}-1|+\Bigg \{-\frac{c_1}{m_1}\\&\qquad -\frac{e_1c_1}{M'b_1x^*}-\frac{c_2z^*}{m'b_2y^{*2}}-\frac{c_2z^*}{m_2y^*}-\frac{e_1c_1}{m'b_1x^*}\\&\qquad -\frac{e_1c_1M'\tau }{m'b_1x^*y^*}\bigg (\frac{e_1c_1y^*}{M'b_1x^*}+\frac{c_2z^*}{m'b_2y^*}+\frac{c_2z^*}{m_2}\bigg )\\&\qquad +\frac{2e_2c_2z^*}{m''b_2y^{*2}}\Bigg \}|{\text{e}}^{Y(t)}-1|+\Bigg \{\frac{c_2}{m_2}\bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )\\&\qquad -\frac{e_2c_2}{M''b_2y^*}+\frac{e_2c_2}{m''b_2y^*}\Bigg \}|{\text{e}}^{Z(t)}-1|\\&\quad \le -\alpha _1X^*|{\text{e}}^{X(t)}-1|-\alpha _2Y^*|{\text{e}}^{Y(t)}-1| \\&\qquad -\alpha _3Z^*|{\text{e}}^{Z(t)}-1|, \end{aligned} \end{aligned}$$
(3.32)

where

$$\begin{aligned} \begin{aligned} \alpha _1&=\Bigg \{\bigg (\frac{r}{K}-\frac{c_1y^*}{mb_1x^{*2}}-\frac{c_1y^*}{m_1x^*}\bigg )\\&\quad -\frac{2e_1c_1y^*}{m'b_1x^*}\bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )\Bigg \}>0,\\ \alpha _2&=\Bigg \{\frac{c_1}{m_1}+\frac{e_1c_1}{M'b_1x^*}-\frac{c_2z^*}{m'b_2y^{*2}}-\frac{c_2z^*}{m_2y^*}-\frac{e_1c_1}{m'b_1x^*}\\&\quad -\frac{e_1c_1M'\tau }{m'b_1x^*y^*}\bigg (\frac{e_1c_1y^*}{M'b_1x^*}+\frac{c_2z^*}{m'b_2y^*}+\frac{c_2z^*}{m_2}\bigg )\\&\quad -\frac{2e_2c_2z^*}{m''b_2y^{*2}}\Bigg \}>0,\\ \alpha _3&=\Bigg \{-\frac{c_2}{m_2}\bigg (1+\frac{e_1c_1M'\tau }{m'b_1x^*}\bigg )+\frac{e_2c_2}{M''b_2y^*}-\frac{e_2c_2}{m''b_2y^*}\Bigg \}>0. \end{aligned} \end{aligned}$$

Since the model system (2.1) is positive invariant, for all \(t>T^*\), we have

$$\begin{aligned} x^*|{\text{e}}^{X(t)}|=x(t)>m, \quad y^*|{\text{e}}^{Y(t)}|=y(t)>m', \quad z^*|{\text{e}}^{Z(t)}|=z(t)>m''. \end{aligned}$$

Using mean value theorem, we have

$$\begin{aligned} x^*|{\text{e}}^{X(t)}-1|&=x^*{\text{e}}^{\theta _1(t)}|X(t)|>m|X(t)|,\\ y^*|{\text{e}}^{Y(t)}-1|&=y^*{\text{e}}^{\theta _1(t)}|Y(t)|>m'|Y(t)|,\\ z^*|{\text{e}}^{Z(t)}-1|&=z^*{\text{e}}^{\theta _1(t)}|Z(t)|>m''|Z(t)|, \end{aligned}$$

where \(x^*{\text{e}}^{\theta _1(t)}\) lies between \(x^*\) and x(t), \(y^*{\text{e}}^{\theta _1(t)}\) lies between \(y^*\) and y(t) and \(z^*{\text{e}}^{\theta _1(t)}\) lies between \(z^*\) and z(t). Therefore,

$$\begin{aligned} D^+V(t)&\le -\alpha _1m|X(t)|-\alpha _2m'|Y(t)|-\alpha _3m''|Z(t)|\nonumber \\&\le -\gamma (|X(t)|+|Y(t)|+|Z(t)|), \end{aligned}$$
(3.33)

where \(\gamma = \min \{\alpha _1 m,\alpha _2 m',\alpha _3 m''\}\).

Noting that \(V(t)>|X(t)|+|Y(t)|+|Z(t)|\). Hence, by using Eq. (3.33) and Lyapunov’s direct method, we can conclude that the zero solution of the reduced system (3.20)–(3.22) is globally asymptotically stable. Therefore, the positive equilibrium of the original model system (2.1) is globally asymptotically stable. \(\square\)

3.5 Stability and direction of the Hopf bifurcation

This section is based on the numerical analysis of Hopf bifurcation theory by using center manifold theorem and normal form theory [51], where the critical value of time delay is denoted by \(\tau =\tau _0\) at which Eq. (3.8) has a pair of purely imaginary roots \(\pm i\omega _0\) and system undergoes a Hopf bifurcation at equilibrium \(E^*\).

Let \(x_1=x-x^*\) , \(x_2=y-y^*\) , \(x_3=z-z^*\) , \(\mu =\tau -\tau _0\) where \(\mu \in \mathfrak {R}\). Rescaling the time by \(t \longrightarrow \frac{t}{\tau }\), the system (2.1) can be written into the following continuous real-valued functions \(C=([-1,0],\mathfrak {R}^3)\) as

$$\begin{aligned} \begin{aligned} {\dot{x}}(t)=L_\mu (x_t)+f(\mu ,x_t), \end{aligned} \end{aligned}$$
(3.34)

where \(x(t)=(x_1(t),x_2(t),x_3(t))^T\in \mathfrak {R}^3, \ x_t(\theta ) = x(t+\theta ), \ \theta \in [-1,0]\) and \(L_\mu :C\rightarrow \mathfrak {R}^3, \ f:\mathfrak {R}\times C\rightarrow \mathfrak {R}^3\) are given, respectively,

$$\begin{aligned} L_\mu (\phi )=(\tau _0+\mu )[J \phi (0)+J' \phi (-1)], \end{aligned}$$
(3.35)

such that

$$\begin{aligned} J = \left( \begin{array}{ccc} \begin{aligned}-\frac{rx^*}{K}+\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}-\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ 0 &{} \begin{aligned}-d_1+\frac{\delta _4c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}-\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}-\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} 0 \end{array}\right) , \end{aligned}$$
$$\begin{aligned} J'=\left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ \\ \begin{aligned}-\frac{\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{e_1c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ 0 &{} 0 &{} 0 \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned}&f(\mu ,\phi )\nonumber \\&\quad =(\tau _0+\mu )\left( \begin{array}{c} \begin{aligned} \bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg ) \phi _{1}^{2}(0) + \frac{\delta _2c_1}{\gamma _1^2}\phi _1(0) \phi _2(0)\end{aligned} \\ \\ \begin{aligned} \frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}\phi _{1}^{2}(-1) -\frac{\delta _2e_1c_1}{\gamma _1^2} \phi _1(-1)\phi _2(-1) +\frac{\delta _4c_2}{\gamma _2^2}\phi _2(0)\phi _3(0) -\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3} \phi _2^2(0) \end{aligned}\\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}\phi _{2}^{2}(0)-\frac{\delta _4e_2c_2}{\gamma _2^2}\phi _2(0)\phi _3(0)\end{aligned} \end{array}\right) , \end{aligned}$$
(3.36)

where \(\delta _1=(b_1x^{*2}-3m_1)\), \(\delta _2=(b_1x^{*2}-m_1)\), \(\delta _3=(b_2y^{*2}-3m_2)\), \(\delta _4=(b_2y^{*2}-m_2)\), \(\gamma _1=(b_1x^{*2}+m_1)\), \(\gamma _2=(b_2y^{*2}+m_2)\) and \(\phi (\theta )=(\phi _1(\theta ),\phi _2(\theta ),\phi _3(\theta ))^T \in C([-1,0],\mathfrak {R}^3)\).

By the Riesz representation theorem, there exists a function \(\eta (\theta ,\mu )\) of bounded variation for \(\theta \in [-1,0]\), such that

$$\begin{aligned} L_\mu \phi = \int _{-1}^{0} {\text{d}}\eta (\theta ,\mu )\phi (\theta ), \quad for \quad \phi \in C. \end{aligned}$$
(3.37)

In fact, we can take

$$\begin{aligned} \eta (\theta ,\mu )=(\tau _0+\mu )[J \delta (\theta )+J' \delta (\theta +1)], \end{aligned}$$
(3.38)

where \(\delta (\theta )\) is the Dirac delta function.

For \(\phi \in C([-1,0],\mathfrak {R}^3)\), define

$$\begin{aligned} A(\mu )\phi = {\left\{ \begin{array}{ll} \frac{{\text{d}}\phi (\theta )}{{\text{d}}\theta }, &{} \theta \in [-1,0),\\ \\ \int _{-1}^{0} \phi (s) {\text{d}}\eta (s,\mu ), &{} \theta =0, \end{array}\right. } \end{aligned}$$
(3.39)

and

$$\begin{aligned} R(\mu )\phi = {\left\{ \begin{array}{ll} 0, &{} \theta \in [-1,0),\\ \\ f(\mu ,\phi ), &{} \theta =0. \end{array}\right. } \end{aligned}$$
(3.40)

Then, Eq. (3.34) equivalent to the following equation,

$$\begin{aligned} \dot{x_t}=A(\mu ) x_t +R(\mu ) x_t, \end{aligned}$$
(3.41)

where \(x_t(\theta )=x(t+\theta )\) for \(\theta \in [-1,0]\).

For \(\psi \in C^1([0,1],(\mathfrak {R}^3)^*)\), we define the adjoint of A as

$$\begin{aligned} A^* \psi (s)= {\left\{ \begin{array}{ll} -\frac{{\text{d}}\psi (s)}{{\text {d}}s} &{} s\in (0,1],\\ \\ \int _{-1}^0 \psi (-t){\text{d}}\eta ^T (t,0), &{} s = 0, \end{array}\right. } \end{aligned}$$
(3.42)

and a bilinear inner product is given by

$$\begin{aligned} \langle \psi (s), \phi (\theta ) \rangle ={\bar{\psi }}(0)\phi (0)-\int _{-1}^0 \int _0^\theta {\bar{\psi }}(\xi -\theta ) {\text{d}}\eta (\theta )\phi (\xi ){\text{d}}\xi , \end{aligned}$$
(3.43)

where \(\eta (\theta )=\eta (\theta ,0)\). Then, A(0) and \(A^*\) are adjoint operators.

For further calculation, we assume that \(i\omega _0\tau _0\) and \(-i\omega _0\tau _0\) are eigenvalues of A(0) and \(A^*\), respectively. Now, let \(q(\theta )=(1,\alpha _2,\alpha _3)^T {\text{e}}^{i\omega _0\tau _0\theta }\) and \(q^*(s)=N (1,\alpha _2^*,\alpha _3^*) {\text{e}}^{i\omega _0\tau _0 s}\) are the eigenvector of A(0) and \(A^*(0)\) corresponding to \(+i\omega _0\tau _0\) and \(-i\omega _0\tau _0\), respectively.

Then,

$$\begin{aligned} Aq(\theta )=i\omega _0\tau _0q(\theta ), \end{aligned}$$
(3.44)

for \(\theta =0\), we obtained

$$\begin{aligned}&\tau _0\left( \begin{array}{ccc} \begin{aligned}i\omega _0+\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ \begin{aligned}{\text{e}}^{-i\omega _0\tau _0}\frac{\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}i\omega _0-\frac{\delta _4c_2z^*}{\gamma _2^2} +d_1 -{\text{e}}^{-i\omega _0\tau _0}\frac{e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}i\omega _0\end{aligned} \end{array}\right) q(0)\nonumber =\left( \begin{array}{ccc} 0 \\ \\ 0 \\ \\ 0 \end{array}\right) . \end{aligned}$$
(3.45)

Solving the system of equations, we get

$$\begin{aligned} \alpha _2=\frac{2b_1x^*y^*}{\gamma _1}-\frac{r\gamma _1}{Kc_1}-\frac{i\omega _0\gamma _1}{c_1x^*}, \end{aligned}$$

and

$$\begin{aligned} \alpha _3=-\frac{\alpha _2\delta _4e_2c_2z^*}{i\omega _0\gamma _2^2}. \end{aligned}$$

Similarly, let

$$\begin{aligned} A^*q^*(s)=-i\omega _0\tau _0q^*(s), \end{aligned}$$
(3.46)

where

$$\begin{aligned} \begin{aligned} \alpha _{2}^{*}=\frac{2b_1x^{*2}}{{\text{e}}^{-i\omega _0\tau _0}\delta _2e_1}-\frac{rx^*\gamma _1^2}{{\text{e}}^{-i\omega _0\tau _0}\delta _2Ke_1c_1y^*}+\frac{i\omega _0\gamma _1^2}{{\text{e}}^{-i\omega _0\tau _0}\delta _2e_1c_1y^*}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \alpha _{3}^{*}=\frac{c_2y^*\alpha _{2}^{*}}{i\omega _0\gamma _2}. \end{aligned}$$

Under the normalization condition \(\langle q^*(s),q(\theta ) \rangle = 1\), we have

$$\begin{aligned} N=\frac{1}{{\overline{D}}}, \end{aligned}$$

where

$$\begin{aligned} D=1+\alpha _2{\bar{\alpha }}_{2}^{*}+\alpha _3{\bar{\alpha }}_{3}^{*}+\tau _0{\bar{\alpha }}_{2}^{*}\Bigg [ -\frac{\delta _2e_1c_1y^*}{\gamma _1^2}+\alpha _2\frac{e_1c_1x^*}{\gamma _1} \Bigg ]{\text{e}}^{-i\omega _0\tau _0}. \end{aligned}$$

Now in the remainder section, following in the same manner as given in [51], we obtained

$$\begin{aligned}&g(z,{\bar{z}})\nonumber \\&\quad =\tau _0 {\bar{N}} (1,{\bar{\alpha }}_2^*, {\bar{\alpha }}_3^*) \left( \begin{array}{c} \begin{aligned} \bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg ) \phi _{1}^{2}(0) + \frac{\delta _2c_1}{\gamma _1^2}\phi _1(0) \phi _2(0)\end{aligned} \\ \\ \begin{aligned} \frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}\phi _{1}^{2}(-1) -\frac{\delta _2e_1c_1}{\gamma _1^2} \phi _1(-1)\phi _2(-1) +\frac{\delta _4c_2}{\gamma _2^2}\phi _2(0)\phi _3(0) -\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3} \phi _2^2(0) \end{aligned}\\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}\phi _{2}^{2}(0)-\frac{\delta _4e_2c_2}{\gamma _2^2}\phi _2(0)\phi _3(0)\end{aligned} \end{array}\right), \end{aligned}$$
(3.47)

such that

$$\begin{aligned} \phi _1(0)&= z+ {\bar{z}} + W_{20}^{(1)} (0) \frac{z^2}{2} + W_{11}^{(1)} (0) z {\bar{z}} + W_{02}^{(1)} (0) \frac{{\bar{z}}^2}{2} \\&\quad +\ldots ,\\ \phi _2(0)&= \alpha _2 z+ {\bar{\alpha }}_2 {\bar{z}} + W_{20}^{(2)} (0) \frac{z^2}{2} + W_{11}^{(2)} (0) z {\bar{z}} + W_{02}^{(2)} (0) \frac{{\bar{z}}^2}{2} \\&\quad +\ldots ,\\ \phi _3(0)&=\alpha _3z+{\bar{\alpha }}_3{\bar{z}}+W_{20}^{(3)}(0)\frac{z^2}{2}+W_{11}^{(3)}(0)z{\bar{z}}+W_{02}^{(3)}(0)\frac{{\bar{z}}^2}{2}\\&\quad +\ldots ,\\ \phi _1(-1)&= z {\text{e}}^{-i\omega _0 \tau _0} + {\bar{z}} {\text{e}}^{i\omega _0 \tau _0} + W_{20}^{(1)} (-1) \frac{z^2}{2} + W_{11}^{(1)} (-1) z {\bar{z}} \\&\quad + W_{02}^{(1)} (-1) \frac{{\bar{z}}^2}{2} +\ldots ,\\ \phi _2(-1)&=\alpha _2z {\text{e}}^{-i\omega _0 \tau _0} + {\bar{\alpha }}_2{\bar{z}} {\text{e}}^{i\omega _0 \tau _0} + W_{20}^{(2)} (-1) \frac{z^2}{2} \\&\quad + W_{11}^{(2)} (-1) z {\bar{z}} + W_{02}^{(2)} (-1) \frac{{\bar{z}}^2}{2} +\ldots . \end{aligned}$$

From Eq. (3.47), we have the following quantities:

$$\begin{aligned} \begin{aligned} g_{20} &=2\tau _0{\bar{N}}\Bigg [ \bigg (\bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg ) \nonumber \\ &\quad +\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}{\bar{\alpha }}_{2}^{*}{\text{e}}^{-2i\omega _0\tau _0}\bigg ) \\&\quad +\alpha _2\bigg (\frac{\delta _2c_1}{\gamma _1^2}-\frac{\delta _2e_1c_1}{\gamma _1^2}{\bar{\alpha }}_{2}^{*}{\text{e}}^{-2i\omega _0\tau _0}\bigg )\\&\quad + \alpha _2\alpha _3 \bigg (\frac{\delta _4c_2}{\gamma _2^2}{\bar{\alpha }}_{2}^{*}-\frac{\delta _4e_2c_2}{\gamma _2^2}{\bar{\alpha }}_{3}^{*}\bigg ) \\&\quad +\alpha _2^2\bigg (-\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{2}^{*}+\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{3}^{*}\bigg ) \Bigg ], \end{aligned} \end{aligned}$$
(3.48)
$$\begin{aligned} \begin{aligned} g_{11}&=2\tau _0{\bar{N}}\Bigg [ \bigg (\bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg ) +\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}{\bar{\alpha }}_{2}^{*}\bigg ) \\&\quad +Re(\alpha _2)\bigg (\frac{\delta _2c_1}{\gamma _1^2}-\frac{\delta _2e_1c_1}{\gamma _1^2}{\bar{\alpha }}_{2}^{*}\bigg ) + Re(\alpha _2{\bar{\alpha }}_3) \bigg (\frac{\delta _4c_2}{\gamma _2^2}{\bar{\alpha }}_{2}^{*}-\frac{\delta _4e_2c_2}{\gamma _2^2}{\bar{\alpha }}_{3}^{*}\bigg ) \\&\quad +\alpha _2{\bar{\alpha }}_2\bigg (-\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{2}^{*} +\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{3}^{*}\bigg ) \Bigg ],\\ g_{02}&=2\tau _0{\bar{N}}\Bigg [ \bigg (\bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg ) +\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}{\bar{\alpha }}_{2}^{*}{\text{e}}^{2i\omega _0\tau _0}\bigg ) \\&\quad +\bar{\alpha _2}\bigg (\frac{\delta _2c_1}{\gamma _1^2}-\frac{\delta _2e_1c_1}{\gamma _1^2}{\bar{\alpha }}_{2}^{*}{\text{e}}^{2i\omega _0\tau _0}\bigg ) + \bar{\alpha _2}\bar{\alpha _3} \bigg (\frac{\delta _4c_2}{\gamma _2^2}{\bar{\alpha }}_{2}^{*} -\frac{\delta _4e_2c_2}{\gamma _2^2}{\bar{\alpha }}_{3}^{*}\bigg ) \\&\quad +{\bar{\alpha }}_2^2\bigg (-\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{2}^{*}+\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_{3}^{*}\bigg ) \Bigg ], \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} g_{21}&=2\tau _0{\bar{N}}\Bigg [ \bigg (-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}\bigg )(2W_{20}^{(1)}(0)+4W_{11}^{(1)}(0))\\&\quad +\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}{\bar{\alpha }}_2^*(2{\text{e}}^{i\omega _0\tau _0}W_{20}^{(1)}(-1)\\&\quad +4{\text{e}}^{-i\omega _0\tau _0}W_{11}^{(1)}(-1))+\frac{\delta _2c_1}{\gamma _1^2}({\bar{\alpha }}_2W_{20}^{(1)}(0)+2\alpha _2W_{11}^{(1)}(0)\\&\quad +W_{20}^{(2)}(0)+2W_{11}^{(2)}(0))-\frac{\delta _2e_1c_1}{\gamma _1^2} {\bar{\alpha }}_2^*({\bar{\alpha }}_2{\text{e}}^{i\omega _0\tau _0}W_{20}^{(1)}(-1) \\&\quad +2\alpha _2{\text{e}}^{-i\omega _0\tau _0}W_{11}^{(1)}(-1) +{\text{e}}^{i\omega _0\tau _0}W_{20}^{(2)}(-1) \\&\quad +2{\text{e}}^{-i\omega _0\tau _0}W_{11}^{(2)}(-1))+\bigg (\frac{\delta _4c_2}{\gamma _2^2}{\bar{\alpha }}_2^*-\frac{\delta _4e_2c_2}{\gamma _2^2}{\bar{\alpha }}_3^* \bigg ) ({\bar{\alpha }}_3W_{20}^{(2)}(0) \\&\quad +2\alpha _3W_{11}^{(2)}(0) +{\bar{\alpha }}_2 W_{20}^{(3)}(0) +2\alpha _2W_{11}^{(3)}(0))\\&\quad +\bigg (-\frac{\delta _3b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_2^* +\frac{\delta _3e_2b_2c_2y^*z^*}{\gamma _2^3}{\bar{\alpha }}_3^*\bigg )(2{\bar{\alpha }}_2W_{20}^{(2)}(0)\\&\quad +4\alpha _2W_{11}^{(2)}(0))\Bigg ]. \end{aligned} \end{aligned}$$

We denote \(W_{20}(\theta ) = (W_{20}^{(1)}(\theta ),W_{20}^{(2)}(\theta ),W_{20}^{(3)}(\theta ))^T\) and \(W_{11}(\theta ) = (W_{11}^{(1)}(\theta ),W_{11}^{(2)}(\theta ),W_{11}^{(3)}(\theta ))^T\). By computing, we obtained

$$\begin{aligned} \begin{aligned} W_{20}(\theta )=-\frac{g_{20}}{i\omega _0\tau _0} q(\theta ) - \frac{{\bar{g}}_{02}}{3i\omega _0\tau _0} {\bar{q}}(\theta ) + E_1 {\text{e}}^{2i\omega _0\tau _0\theta }, \end{aligned} \end{aligned}$$
(3.49)

and

$$\begin{aligned} \begin{aligned} W_{11}(\theta )=\frac{g_{11}}{i\omega _0\tau _0} q(0) {\text{e}}^{i\omega _0\tau _0\theta } - \frac{{\bar{g}}_{11}}{i\omega _0\tau _0} {\bar{q}}(0) {\text{e}}^{-i\omega _0\tau _0\theta } + E_2, \end{aligned} \end{aligned}$$
(3.50)

where \(E_1 = (E_1^{(1)},E_1^{(2)},E_1^{(3)})\) and \(E_2 = (E_2^{(1)},E_2^{(2)},E_2^{(3)}) \in \mathfrak {R}^3\) are the constant vectors, which can be determined by using [51].

Therefore,

$$\begin{aligned} E_1= \frac{2}{M_1} \left( \begin{array}{c} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1\alpha _2}{\gamma _1^2}\end{aligned} \\ \\ \begin{aligned} \Bigg \{\frac{\delta _1e_1b_1c_1x^*y^*{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^3} -\frac{\delta _2e_1c_1\alpha _2{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2\alpha _2\alpha _3}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} \Bigg \} \end{aligned} \\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} -\frac{\delta _4e_2c_2\alpha _2\alpha _3}{\gamma _2^2}\end{aligned} \end{array}\right) . \end{aligned}$$

Solving this system for \(E_1\), we have

$$\begin{aligned}&E_{1}^{(1)}\\&\quad =\frac{2}{M_1} \left| \begin{array}{ccc} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1\alpha _2}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ \begin{aligned} \frac{\delta _1e_1b_1c_1x^*y^*{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^3} -\frac{\delta _2e_1c_1\alpha _2{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2\alpha _2\alpha _3}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} \end{aligned} &{} \begin{aligned} 2i\omega _0 -\frac{\delta _4c_2z^*}{\gamma _2^2} &{} \\ +d_1-\frac{{\text{e}}^{2i\omega _0\tau _0}e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} -\frac{\delta _4e_2c_2\alpha _2\alpha _3}{\gamma _2^2}\end{aligned} &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}2i\omega _0\end{aligned} \end{array}\right| , \\&E_{1}^{(2)}\\&\quad =\frac{2}{M_1}\left| \begin{array}{ccc} \begin{aligned}2i\omega _0+\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1\alpha _2}{\gamma _1^2}\end{aligned} &{} 0 \\ \\ \begin{aligned}\frac{{\text{e}}^{2i\omega _0\tau _0}\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{\delta _1e_1b_1c_1x^*y^*{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^3} -\frac{\delta _2e_1c_1\alpha _2{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2\alpha _2\alpha _3}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} -\frac{\delta _4e_2c_2\alpha _2\alpha _3}{\gamma _2^2}\end{aligned} &{} \begin{aligned}2i\omega _0\end{aligned} \end{array}\right| , \\&E_{1}^{(3)}\\&\quad =\frac{2}{M_1} \left| \begin{array}{ccc} \begin{aligned}2i\omega _0+\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1\alpha _2}{\gamma _1^2}\end{aligned} \\ \\ \begin{aligned}\frac{{\text{e}}^{2i\omega _0\tau _0}\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned} 2i\omega _0 -\frac{\delta _4c_2z^*}{\gamma _2^2} &{} \\ +d_1-\frac{{\text{e}}^{2i\omega _0\tau _0}e_1c_1x^*}{\gamma _1} &{} \end{aligned} &{} \begin{aligned}\frac{\delta _1e_1b_1c_1x^*y^*{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^3} -\frac{\delta _2e_1c_1\alpha _2{\text{e}}^{-2i\omega _0\tau _0}}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2\alpha _2\alpha _3}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2^2}{\gamma _2^3} -\frac{\delta _4e_2c_2\alpha _2\alpha _3}{\gamma _2^2}\end{aligned} \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned}&M_1\\&\quad =\left| \begin{array}{ccc} \begin{aligned}2i\omega _0+\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ \begin{aligned}\frac{{\text{e}}^{2i\omega _0\tau _0}\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned} 2i\omega _0 -\frac{\delta _4c_2z^*}{\gamma _2^2} +d_1-\frac{{\text{e}}^{2i\omega _0\tau _0}e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}2i\omega _0\end{aligned} \end{array}\right| . \end{aligned}$$

Similarly,

$$\begin{aligned} E_2= \frac{2}{M_2} \left( \begin{array}{c} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1Re(\alpha _2)}{\gamma _1^2}\end{aligned} \\ \\ \begin{aligned}\Bigg \{\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}-\frac{\delta _2e_1c_1Re(\alpha _2)}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3} \Bigg \}\end{aligned} \\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}-\frac{\delta _4e_2c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2}\end{aligned} \end{array}\right) . \end{aligned}$$

Solving this system for \(E_2\), we have

$$\begin{aligned}&E_2^{(1)}\\&\quad =\frac{2}{M_2} \left| \begin{array}{ccc} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1Re(\alpha _2)}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ \begin{aligned}\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}-\frac{\delta _2e_1c_1Re(\alpha _2)}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}\end{aligned} &{} \begin{aligned} -\frac{\delta _4c_2z^*}{\gamma _2^2} +d_1-\frac{e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}-\frac{\delta _4e_2c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2}\end{aligned} &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} 0 \end{array}\right| , \\&E_2^{(2)}\\&\quad =\frac{2}{M_2} \left| \begin{array}{ccc} \begin{aligned}\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}-\frac{r}{K} -\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1Re(\alpha _2)}{\gamma _1^2}\end{aligned} &{} 0 \\ \\ \begin{aligned}\frac{\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}-\frac{\delta _2e_1c_1Re(\alpha _2)}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}-\frac{\delta _4e_2c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2}\end{aligned} &{} 0 \end{array}\right| , \end{aligned}$$

and

$$\begin{aligned}&E_2^{(3)}\\&\quad =\frac{2}{M_2} \left| \begin{array}{ccc} \begin{aligned}\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} \begin{aligned}-\frac{r}{K}-\frac{\delta _1b_1c_1x^*y^*}{\gamma _1^3}+\frac{\delta _2c_1Re(\alpha _2)}{\gamma _1^2}\end{aligned} \\ \\ \begin{aligned}\frac{\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned} -\frac{\delta _4c_2z^*}{\gamma _2^2} +d_1-\frac{e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{\delta _1e_1b_1c_1x^*y^*}{\gamma _1^3}-\frac{\delta _2e_1c_1Re(\alpha _2)}{\gamma _1^2} &{} \\ +\frac{\delta _4c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2} -\frac{\delta _3b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} \begin{aligned}\frac{\delta _3e_2b_2c_2y^*z^*\alpha _2{\bar{\alpha }}_2}{\gamma _2^3}-\frac{\delta _4e_2c_2Re(\alpha _2{\bar{\alpha }}_3)}{\gamma _2^2}\end{aligned} \end{array}\right| , \end{aligned}$$

where

$$\begin{aligned} M_2=\left| \begin{array}{ccc} \begin{aligned}\frac{rx^*}{K}-\frac{2b_1c_1x^{*2}y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned}\frac{c_1x^*}{\gamma _1}\end{aligned} &{} 0 \\ \\ \begin{aligned}\frac{\delta _2e_1c_1y^*}{\gamma _1^2}\end{aligned} &{} \begin{aligned} -\frac{\delta _4c_2z^*}{\gamma _2^2} +d_1-\frac{e_1c_1x^*}{\gamma _1} &{}\end{aligned} &{} \begin{aligned}\frac{c_2y^*}{\gamma _2}\end{aligned} \\ \\ 0 &{} \begin{aligned}\frac{\delta _4e_2c_2z^*}{\gamma _2^2}\end{aligned} &{} 0 \end{array}\right| . \end{aligned}$$

Consequently, we determine the value of \(W_{20}(\theta )\) and \(W_{11}(\theta )\) from Eqs. (3.49) and (3.50). The value of \(g_{21}\) can be expressed by delay and parameters in Eq. (3.48). Hence, we will compute the different values:

$$\begin{aligned} \begin{aligned} c_1(0)&= \frac{i}{2\omega _0\tau _0} \bigg ( g_{20}g_{11} - 2|g_{11}|^2 -\frac{|g_{02}|^2}{3} \bigg ) + \frac{g_{21}}{2},\\ \mu _2&=-\frac{\mathfrak {R}\{c_1(0)\}}{\mathfrak {R}\{\lambda '(\tau _0)\}},\\ \beta _2&= 2\mathfrak {R}\{c_1(0)\},\\ T_2&= -\frac{\mathfrak {I}\{c_1(0)\}+\mu _2\mathfrak {I}\{\lambda '(\tau _0)\}}{\omega _0\tau _0}. \end{aligned} \end{aligned}$$
(3.51)

The above values determine the bifurcating periodic solution at the critical value \(\tau _0\) in the center manifold.

Theorem 4

For Eq. (3.51), we have following results:

  1. (i)

    Direction of the Hopf bifurcation is supercritical (subcritical) if \(\mu _2>0 (\mu _2<0)\).

  2. (ii)

    Stability of the bifurcating periodic solution is stable (unstable) if \(\beta _2<0(\beta _2>0)\).

  3. (iii)

    Period of the bifurcating periodic solution increases (decreases) if \(T_2>0(T_2<0)\).

4 Results

In this section, we perform numerical simulations to understand the mechanism that avoid the extinction of species and stabilizes the chaotic system. For that purpose, we have plotted the bifurcation diagram, time series and phase portrait of the model system (2.1). We choose the following set of parameters value;

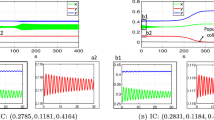
$$\begin{aligned} r&=0.7,\\ K&=28,\\ c_1&=0.65,\\ c_2&=0.45,\\ b_1&=0.025,\\ b_2&=0.035,\\ m_1&=15,\\ m_2&=13,\\ d_1&=0.23,\\ d_2&=0.15,\\ e_1&=0.9,\\ e_2&=0.99. \end{aligned}$$

For the above set of parameters value, we get the value of the interior equilibrium point \(E^*(x^*,y^*,z^*) = (13.7777, 4.6440, 5.4312)\) which is locally asymptotically stable for \(r=0.3\) (c.f., Fig. 1a). We have substantiated the dynamical behavior of the model system (2.1) without delay for different parameters range which are enlisting in Table 1 and observe the effect of time delay in the same parametric value.

Table 1 Dynamical outcome of model system (2.1) for different parameters range at \(\tau =0\)
Full size table
Fig. 1
figure 1

a Time series representation for model system (2.1) with \(r=0.3\) at \(\tau =0\), b bifurcation diagram of time lag \(\tau\) versus population density x(t), y(t), and z(t) for model system (2.1) with \(r=0.3\)

Full size image

Taking the above set of parameter values with \(r=0.3\), we have plotted the bifurcation diagram between time lag \(\tau\) and population density x(t), y(t), z(t) in the interval \(\tau \in [0, 8]\) in which all the population bifurcates for the two values of time delay, i.e., \(\tau _0^1=1.89\) and \(\tau _0^2=6.825\) (c.f., Fig. 1b). To the justification of bifurcation diagram of Fig. 1b, we have plotted time series in which one can see that model system (2.1) remains stable when \(\tau < \tau _0^1 = 1.89\) (c.f., Fig. 2a) and as we increase the value of \(\tau\) by \(\tau _0^1\), system becomes unstable (c.f., Fig. 2b) and at the critical value \(\tau =\tau _0^1=1.89\), model system (2.1) undergoes Hopf bifurcation. Further, we can see the extinction in top predator after certain oscillation in the range of \(\tau\), i.e., top predator shows limit cycle behavior in the range \(1.89 \le \tau < 2.72\) and after that extinction has been observed in the range \(2.72 \le \tau < 6.825\) (c.f., Fig. 2c), whereas limit cycle behavior is obtained for prey and middle predator in the range \(1.89 \le \tau < 6.825\). When \(\tau \ge \tau _0^2 = 6.825\), limit cycle behavior disappears through second Hopf bifurcation and system again shows stable behavior for all the population (c.f., Fig. 2d). Now, we choose \(r=0.7\) and kept other parameters are fixed. A limit cycle behavior is observed for model system (2.1) with \(\tau = 0\) (c.f., Fig. 3a). By incorporating \(\tau\) at this situation, a stable focus is observed by increasing the value of \(\tau\) which is shown by the bifurcation diagram (c.f., Fig. 3b). It is also justified by the phase space diagram that \(\tau =1.5\), the system shows limit cycle behavior and \(\tau =4\), the system shows a stable focus (c.f., Fig. 4).

Fig. 2
figure 2

Time series for model system (2.1) with \(r=0.3\) at a \(\tau =1.5\), b \(\tau =2.3\), c \(\tau =3\), d \(\tau =7\)

Full size image
Fig. 3
figure 3

a Phase space representation for model system (2.1) with \(r=0.7\) at \(\tau =0\), b bifurcation diagram of time lag \(\tau\) versus population density x(t), y(t), and z(t) for model system (2.1) with \(r=0.7\)

Full size image
Fig. 4
figure 4

a Phase space representation for model system (2.1) with \(r=0.7\) at a \(\tau =1.5\), b \(\tau =4\)

Full size image

To understand the dynamical behavior of model system (2.1) with respect to carrying capacity K, we have chosen \(K=33\) and kept other parameters are fixed. Irregular oscillation is observed for model system (2.1) with \(\tau = 0\) (c.f., Fig. 5a). We have chosen a window of \(0.0 \le \tau \le 7.0\) and plotted the bifurcation diagram between time delay and successive maxima of x, y, z in the range [0.0, 35.0], [0.0, 25.0] and [0.0, 25.0], respectively, at \(K=33\) (c.f., Fig. 5b–d). To verify the dynamical behavior of Fig. 5b–d, we have also drawn time series and phase space diagram for four different conditions, i.e., stable focus, periodic solution of order one, periodic solution of order two and chaos. When \(\tau < 0.25\), the system shows chaotic behavior. As the value of the time delays \(\tau\) increases, the system shows periodic solution of order two, then reduces to a limit cycle and finally shows a stable focus for a large value of \(\tau\). Fig. 6a–d shows different nature of system for different values of \(\tau\), i.e., \(\tau = 0.25, 1.5, 2.8\) and 5, respectively. Similarly, we have chosen a window of \(0 \le \tau \le 9\) at \(b_1=0.05\) and \(0 \le \tau \le 6\) at \(b_2=0.06\) and plotted the bifurcation diagram between time delay and successive maxima of x, y, z, respectively (c.f., Fig. 7b–d and 8b–d). In Figs. 7 and 8, one can see for the increasing value of time delay \(\tau\) stabilizes the chaotic behavior of the model system. This result shows that the obtained outcomes are highly affected in the presence of time delay \(\tau.\)

Fig. 5
figure 5

a Time series representation for model system (2.1) with \(K=33\) at \(\tau =0\), b–d bifurcation diagram of time lag \(\tau\) versus population density x(t), y(t), and z(t) for model system (2.1) with \(K=33\)

Full size image
Fig. 6
figure 6

Time series and phase space for model system (2.1) with \(K=33\) at a \(\tau =0.25\), b \(\tau =1.5\), c \(\tau =2.8\), d \(\tau =5\)

Full size image
Fig. 7
figure 7

a Phase space representation for model system (2.1) with \(b_1=0.05\) at \(\tau =0\), b–d bifurcation diagram of time lag \(\tau\) versus population density x(t), y(t), and z(t) for model system (2.1) with \(b_1=0.05\)

Full size image
Fig. 8
figure 8

a Phase space representation for model system (2.1) with \(b_2=0.06\) at \(\tau =0\), b–d bifurcation diagram of time lag \(\tau\) versus population density x(t), y(t), and z(t) for model system (2.1) with \(b_2=0.06\)

Full size image

5 Discussions

In this article, we have explored the dynamics through the defense mechanism adopted by phytoplankton and zooplankton in the presence of fish population. The influence of time delay is studied theoretically with numerical investigation. It has been observed that some time delay is required in the DVM strategy adopted by zooplankton. We have summarized and made a needful comparison of the present study with some previous studies.

  1. 1.

    A plankton–fish interaction with the hybridization of Holling type III and MH-type function response is studied by Raw and Mishra [53], but the effect of time delay on the species dynamics has been neglected. Assume that time delay in the form of gestation, predation, digestion, traveling, etc., fascinated the area of plankton dynamics.

  2. 2.

    Sharma et al. [54] investigated the interaction between toxin-producing phytoplankton (TPP) and zooplankton with the assumption that zooplankton predation must take some time delay \(\tau\). Zhang and Rehim [55] investigated a toxic phytoplankton–zooplankton system with the fact that toxin liberation must take some time variation \(\tau\) and observed that time delay complicates the stability and bifurcation of the system. But the influence of top predator on the system dynamics has ignored. A delayed prey–predator model in the presence of top predator is more appropriate to explore the consequences of the mechanism adopted by them.

  3. 3.

    Some existing studies have focused on studying the toxin-produced phytoplankton by using an independent parameter (toxication rate) [7, 46], but the current work has been adopted a distinct approach for analyzing the relationship among toxin-produced phytoplankton, zooplankton and planktivorous fish population by assuming MH-type functional response.

  4. 4.

    We have extensively studied the dynamics of the plankton–fish interaction model (2.1) with time delay corresponding to the all feasible equilibria. Zooplankton are usually tried to skip those area where the prey density is very high due to adverse effect of toxic substance released by phytoplankton. Motivated by these observations, we have modeled the predator feeding through MH-type functional response which ensures depletion in per capita predation rate of zooplankton at sufficiently thick phytoplankton density due to toxicity.

  5. 5.

    Agrawal et al. [56] focused on prey–predator problems considering prey, specialist predator and generalist predator where the generalist predator grows sexually. They used Holling type IV and Beddington–DeAngelis-type functional response to describe the relationship between prey and predators and observed a scenario of double Hopf bifurcation. But, here we have chosen all the species of specialist type and concentrated on the defense mechanism which strongly helps in survivorship of phytoplankton and zooplankton and becomes a reason for fish extinction.

  6. 6.

    Table 1 demonstrates the dynamical outcome corresponding to the different parameters' restriction in the absence of delay, mainly examining the role of r, K, \(b_1\) and \(b_2\). Figure 1b equivalently reveals the significance of defense ability with the importance of time delay \(\tau\). If the phytoplankton’s growth rate is sufficiently small, then one can clearly see the extinction in the fish population with the variation in \(\tau\), and if we slightly increase the value of \(\tau\) after a certain interval, all the species stabilize together. This result is agreeable with a real ecosystem. Consequently, our model system exhibits rich dynamics which has not been overlooked earlier in such models, which also shows the existence of double Hopf bifurcation. Figure 3b shows the small change in phytoplankton’s growth rate destabilized the dynamics and with variation in \(\tau\) stabilizes the whole plankton dynamics.

  7. 7.

    Our numerical investigation also shows under the consequences of time delay, the system exhibits chaotic and periodic solution of order two, periodic solution of order one (i.e., limit cycle) and stable focus behavior with the increasing value of \(\tau\) (c.f., Figs. 5b–d, 7b–d, 8b–d). In general, time delay enhances the system complexity [44, 57], but in our case, increasing the value of time delay reduces the complexity through period-doubling cascade, and finally, the whole system becomes stable. This finding reveals the importance of time delay in a real biological system.

Based on the current study, the dependence of plankton–fish interaction on time delay is significantly more realistic than a system without time delay. We also noticed a vital change in plankton–fish interaction for varying time delay parameter \(\tau\) by observing chaos, limit cycle, stable focus, extinction behavior, Hopf bifurcation and double Hopf bifurcation.

6 Conclusion

In this paper, we have proposed a tri-tropic food chain model for plankton–fish dynamics with Monod–Haldane-type functional response. The choice of such functional response fits significantly as a repulsive effect on zooplankton due to the toxicity of phytoplankton. Similarly, zooplankton uses diel vertical migration as a defensive strategy. We have studied the effect of time delay and defense mechanism adopted by plankton. The dynamical behavior for the model system is analyzed in the presence of time delay. The local stability conditions of all the feasible equilibria have been discussed. The interior equilibrium point \(E^*(x^*,y^*,z^*)\) is locally as well as globally asymptotic stable under certain conditions. We have also derived the conditions for stability and direction of the Hopf bifurcation. Our study shows that the defense mechanism adopted by phytoplankton and zooplankton in the presence of time delay plays an important role in the dynamical change of the planktonic system. The ability of defense maintains the survival of prey and middle predator in the presence of the top predator. We observed extinction in top predator due to time delay with moderate value of intrinsic growth rate of prey (c.f., Fig. 1b). Such extinction can be avoided with increasing the value of intrinsic growth rate (c.f., Fig. 3b). Thus, the intrinsic growth rate of prey (i.e., r) and time delay (i.e., \(\tau\)) are two important parameters that control the system dynamics. Further, the large value of \(\tau\) can stabilize the system as well as help to avoid the extinction of top predators due to the negative effect of defense (c.f., Fig. 2). Some other parameters also influence the system dynamics, and for a different parametric range, chaotic dynamics are observed in the absence of time delay (c.f., Figs. 5a, 7a, 8a). In the absence of time delay or for smaller values, system shows the chaotic behavior but by increasing the value of \(\tau\), the system becomes stable (c.f., Figs. 5b–d, 7b–d, 8b–d). The system shows the positive impact of time delay that stabilizes the chaotic dynamics of the proposed system. If the time delay is varied by some critical value, the interior equilibrium of the system switches from stable to unstable and vice versa. It is remarkable that the occurrence of double Hopf bifurcation depends on the value of r because as we take the value of r as 0.7 or larger, no double Hopf bifurcation scenario is observed. Some features require further investigation as collaborative behavior of time delay with diffusion in the presence of defense mechanism.