1 Introduction

Fibrous networks, consisting of long fibres oriented predominantly within one plane, form the basic structure of several materials, including paper [1], electrospun membranes [2,3,4], needle-punched [5, 6] and spun-bonded non-wovens [7], glass wool [8] and mats of sintered stainless steel fibres [9]. In spite of their structural similarity, these materials show significant differences in their macroscopic material behaviour due to, e.g. the different material properties, shapes and interactions of the single fibres [10, 11]. This versatility enables the use of fibrous materials in a multitude of different applications ranging from filters, protective clothing, sensors or scaffolds for tissue engineering [12,13,14]. To analyze the large design space of these fibrous materials both analytical considerations [15, 16] and discrete network models [8, 17, 18] are commonly utilised. Both deterministic, e.g. straight or sinusoidal, and non-deterministic random curves can be used to model the shape of the single fibre centre lines [19]. For the generation of the network models, the single fibres need to be distributed within the modelling domain \(\Omega _{\mathrm{c}}\), for which the network properties of interest are computed. Several algorithms exist for the construction of random fibre networks. They typically start with distributing points randomly on a seeding domain \(\Omega _{\mathrm{s}}\). In the next step, the points are either connected through different techniques, such as triangulation or random connection [20, 21], or used as seeds from which fibres originate with random orientation.

The boundaries of the seeding domain \(\partial \Omega _{\mathrm{s}}\) generally pose problems as, e.g. density variations occur in their proximity [22, 23]. For short fibres, a method was proposed to overcome these issues using periodic boundaries or ‘wrapping’, i.e. overhanging parts of fibres leaving the modelling domain are reinserted at the opposite side until the whole fibre is deposited [22, 24,25,26]. For deterministic fibres with lengths orders of magnitude longer than the size of the modelling domain \(\Omega _{\mathrm{c}}\), such as the fibres in electrospun networks (Fig. 2a), wrapping would lead to networks with largely parallel fibres [26] and, if infinite length can be assumed with respect to the size of \(\Omega _{\mathrm{c}}\), one fibre would fill the entire domain [27]. The strategy typically used to distribute long fibres computationally is an algorithm [26,27,28], where the seeding domain is square shaped and of the same size or larger than the modelling domain (\(\Omega _{\mathrm{s}}\ge \Omega _{\mathrm{c}}\)), and the generated fibres are cropped at the boundaries of the modelling domain \(\partial \Omega _{\mathrm{c}}\). We will term this technique square seeding, and study in detail the influence of the seeding domain \(\Omega _{\mathrm{s}}\) on the randomness of the resulting fibre network, defined through evenly distributed fibres, i.e. homogeneous fibre density, and isotropic fibre orientation of the resulting fibre network within the modelling domain \(\Omega _{\mathrm{c}}\). To this end, the resulting fibre density and orientation distribution are assessed analytically and with Monte Carlo simulations for straight fibres. The study shows significant deviations from the ideal random case when the square seeding algorithm is applied, and reveals that the size and shape of the seeding domain have a major effect on the randomness of the final network. An improved seeding method based on an extended circular seeding domain \(\Omega _{\mathrm{s}}\) is therefore proposed and assessed with respect to its capability to generate random networks of straight fibres. Since real network materials typically consist of randomly curved fibres [29], both the square and extended circular seeding are subsequently studied in Monte Carlo simulations with regard to their applicability to random networks of tortuous fibres generated by a random walk.

2 Methods

2.1 Definition of random networks

Due to the discrete nature of a network consisting of a finite number of fibres, true pointwise homogeneity and isotropy can never be achieved. Thus, the term ‘random network’ is used here for networks which would have a homogeneous normalised fibre density \({\hat{P}}({x}_{\mathrm{c}})\) and a normalised isotropic orientation distribution \({\hat{p}}({x}_{\mathrm{c}},\varphi )\) within the modelling domain \(\Omega _{\mathrm{c}}\) in the limit case of an infinite number of sampled fibres. For simplicity and to make the study scale independent, a modelling domain with unit area (\(|\Omega _\mathrm{c}|=1\)) was used and all dimensions were normalised accordingly. Expressing the conditions for a random network analytically, the fibre density

$$\begin{aligned} {\hat{P}}({x}_{\mathrm{c}})&=\frac{P({x}_\mathrm{c})}{C} \end{aligned}$$
(1)

with a normalising factor

$$\begin{aligned} C&=\int _{\Omega _{\mathrm{c}}}P({x}_{\mathrm{c}})d\Omega _{\mathrm{c}} \end{aligned}$$
(2)

and the fibre orientation distribution

$$\begin{aligned} {\hat{p}}({x}_{\mathrm{c}},\varphi )&=\frac{p({x}_\mathrm{c},\varphi )}{c({x}_{\mathrm{c}})} \end{aligned}$$
(3)

with normalisation

$$\begin{aligned} c({x}_{\mathrm{c}})&=\frac{1}{2\pi }\int _{0}^{2\pi }p({x}_\mathrm{c},\varphi )d\varphi \end{aligned}$$
(4)

are constant in the modelling domain, i.e.

$$\begin{aligned} {\hat{P}}({x}_{\mathrm{c}})=\text {const}=1 ,\quad {\hat{p}}({x}_{\mathrm{c}},\varphi )=\text {const}=1\quad \forall {x}_\mathrm{c}\in \Omega _{\mathrm{c}}. \end{aligned}$$
(5)

2.2 Error measures

Error measures are introduced to quantify the deviation of a network from the random case. A global error measure \(E_{\mathrm{h}}\) with respect to the homogeneous density is defined as the maximal absolute difference of the normalised fibre density \({\hat{P}}\) to the homogeneous case (\({\hat{P}}=1\))

$$\begin{aligned} E_{\mathrm{h}}=\max _{\Omega _{\mathrm{c}}}\left( |{\hat{P}}\left({x}_{\mathrm{c}}\right) - 1|\right). \end{aligned}$$
(6)

A scalar local error \(e_{\mathrm{i}}({x}_{\mathrm{c}})\) of isotropy is defined as the integral absolute difference of the normalised orientation distribution \({\hat{p}}\) to the isotropic case (\({\hat{p}}=1\))

$$\begin{aligned} e_{\mathrm{i}}({x}_{\mathrm{c}})=\frac{1}{2\pi }\int _0^{2\pi }|{\hat{p}}({x}_\mathrm{c},\varphi )-1|d\varphi , \end{aligned}$$
(7)

based on which the global error in isotropy

$$\begin{aligned} E_{\mathrm{i}}=\max _{\Omega _{\mathrm{c}}}(e_{\mathrm{i}}({x}_{\mathrm{c}})) \end{aligned}$$
(8)

is calculated as the maximal local error \(e_{\mathrm{i}}({x}_{\mathrm{c}})\).

Fig. 1
figure 1

Seeding. a Modelling \(\Omega _{\mathrm{c}}\) and seeding \(\Omega _{\mathrm{s}}\) domain b Poisson point process, i.e. random introduction of points by sampling coordinates from a uniform distributions in the seeding domain \(\Omega _{\mathrm{s}}\)

Full size image
Fig. 2
figure 2

Fibre generation. a Scanning electron micrograph of an electrospun non-woven as example of a long fibre network (cf. [30]). b Introduction of fibres at previously introduced points with planar orientation sampled from uniform distribution. c Introduction of tortuous fibres generated by a random walk starting at the previously introduced points

Full size image

2.3 Computational network generation

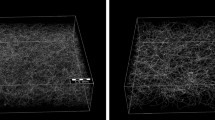
We consider algorithms to generate random networks on the modelling domain \(\Omega _{\mathrm{c}}\) with long fibres, much longer than the characteristic length of \(\Omega _{\mathrm{c}}\), so that they span from one edge to another one of \(\Omega _{\mathrm{c}}\). The modelling domain can generally be arbitrary in shape (Fig. 1a), however, a square area of the specific network is commonly chosen for further studies (Fig. 1b) and in line with \(|\Omega _{\mathrm{c}}|=1\), we consider square domains with unit edge length here. Most algorithms build on an initial step, where seeding points for each fibre are sampled uniformly, i.e. by a Poisson point process [31], on a seeding domain \(\Omega _\mathrm{s}\ge \Omega _{\mathrm{c}}\) (Fig. 1). Although, \(\Omega _{\mathrm{s}}\) can also be of arbitrary shape (Fig. 1a), the common approach [26,27,28] is to use a seeding domain with the same size as the square modelling domain (\(\Omega _\mathrm{s}=\Omega _{\mathrm{c}}\)) and we will refer to this approach as square seeding throughout this contribution. Another approach used previously [17] extends \(\Omega _{\mathrm{s}}\) onto a square area concentric but larger than the modelling domain \(\Omega _{\mathrm{s}}>\Omega _{\mathrm{c}}\) and this method will be referred to as extended square seeding (Figs. 1b, 2b, c). A third method, introduced in this contribution, is based on using a concentric circular seeding domain larger than the modelling domain and we will call this extended circular seeding (Fig. 6a).

Fig. 3
figure 3

Parameters for analytic study. Illustration of seeding point \({x}_{\mathrm{s}}\), sampling point \({x}_{\mathrm{c}}\), opening angle \(\Delta \phi\), in-plane angle \(\varphi\) and the distance \(L_{\mathrm{s}}({x}_{\mathrm{c}},\varphi )\) of \({x}_{\mathrm{c}}\) from the boundary \(\partial \Omega _{\mathrm{s}}\) in the direction specified by \(\varphi\)

Full size image

After seeding, fibres are introduced with random orientation at every seeding point to generate networks of either straight or tortuous fibres (Fig. 2b, c). Straight fibres (Fig. 2b) are introduced as lines with constant orientation angle sampled from a uniform distribution \(\phi \sim \text {Uni} (0,2\pi )\) with respect to an arbitrary but fixed axis. Non-deterministic tortuous fibres (Fig. 2c) are defined through a random walk, or a chain of links with length l [19, 25, 32, 33], and \(l=4\times 10^{-3}\) is chosen here. In particular, following our previous work [19, 26] a worm-like model [34, 35] is used. Thus the first link is introduced at each seeding point with random orientation \(\phi \sim \text {Uni} (0,2\pi )\), and consecutive links are added until the fibre reaches a boundary of \(\Omega _{\mathrm{c}}\). The angle \(\theta\) between two consecutive links is sampled from a Gaussian distribution [19, 34]

$$\begin{aligned} P(\theta )=\frac{1}{\sqrt{2\pi ({l/\ell })}}e^{-\frac{\theta ^2}{2({l/\ell })}}, \end{aligned}$$
(9)

parametrised by the persistence length \(\ell\) [19, 34,35,36]. Noteworthy, the limit case (\(\ell \rightarrow \infty\)) leads to straight fibres.

2.4 Network density for straight fibres

An analytic approach, based on the probability of lines crossing a small circle, was used to evaluate the network’s density distribution in the modelling domain \(\Omega _{\mathrm{c}}\). When sampling the fibre direction from a uniform orientation distribution \(\phi \sim \text {Uni} (0,2\pi )\), the probability of a fibre leaving the seeding point in the angular interval \(\Delta \phi\) is given by

$$\begin{aligned} {\mathcal {P}}(\Delta \phi )=\dfrac{\Delta \phi }{2\pi }. \end{aligned}$$
(10)

Considering a circle with diameter \(\varepsilon\) at point \({x}_\mathrm{c}\) and a distance r to a seeding point \({x}_{\mathrm{s}}\), the ‘opening angle’ \(\Delta \phi\) at the seeding point, i.e. the angle between the two lines connecting \({x}_{\mathrm{s}}\) with the two intersection points of a diameter perpendicular to the line \(\overline{{x}_{\mathrm{s}}{x}_{\mathrm{c}}}\) (Fig. 3), can be calculated by

$$\begin{aligned} \Delta \phi =2\text {arctan}\frac{\varepsilon }{2r}. \end{aligned}$$
(11)

Inserting Eq. (11) in Eq. (10) leads to the probability of the straight fibre emerging at \({x}_\mathrm{s}\) to cross the circle with diameter \(\varepsilon\) at \({x}_{\mathrm{c}}\) as

$$\begin{aligned} {\mathcal {P}}_{\mathrm{cs}}=\dfrac{1}{\pi }\text {arctan}\frac{\varepsilon }{2r}. \end{aligned}$$
(12)

Considering all seeding points \({x}_{\mathrm{s}}\) by integration of \({\mathcal {P}}_{\mathrm{cs}}\) over the seeding domain \(\Omega _{\mathrm{s}}\) gives the probability, proportional to the line density, of a fibre seeded somewhere in the seeding domain \(\Omega _{\mathrm{s}}\) crossing the particular circle centered at \({x}_{\mathrm{c}}\)

$$\begin{aligned} {P}({x}_{\mathrm{c}})=\frac{1}{C}\int _{\Omega _{\mathrm{s}}} {\mathcal {P}}_\mathrm{cs}d\Omega _{\mathrm{s}}, \end{aligned}$$
(13)

where C is a nomalisation factor (Eq. (2)). Evaluating Eq. (13) with the probability Eq. (12) in polar coordinates leads to

$$\begin{aligned} {P}({x}_{\mathrm{c}})&=\frac{1}{C}\int _0^{2\pi }\int _0^{L_{\mathrm{s}}({x}_\mathrm{c},\varphi )}\text {arctan}\left( \frac{\varepsilon }{2r}\right) rdrd\varphi . \end{aligned}$$
(14)

The inner integral of Eq. (14) represents the orientation distribution

$$\begin{aligned} p({x}_{\mathrm{c}},\varphi )&=\int _0^{L_{\mathrm{s}}({x}_\mathrm{c},\varphi )}\text {arctan}\left( \frac{\varepsilon }{2r}\right) rdr \end{aligned}$$
(15)

at \({x}_{\mathrm{c}}\) and can be evaluated as

$$\begin{aligned} \begin{aligned} p({x}_{\mathrm{c}},\varphi )=&\frac{L^2_{\mathrm{s}}}{2}({x}_\mathrm{c},\varphi )\text {arccot}\left( \frac{2L_{\mathrm{s}}({x}_\mathrm{c},\varphi )}{\varepsilon }\right) \\ {}&+\frac{\varepsilon }{4}\left( L_\mathrm{s}({x}_\mathrm{c},\varphi )-\frac{\varepsilon }{2}\arctan \left( \frac{2L_\mathrm{s}({x}_{\mathrm{c}},\varphi )}{\varepsilon }\right) \right) . \end{aligned} \end{aligned}$$
(16)

The Taylor expansion of Eq. (16) is given by

$$\begin{aligned} p({x}_{\mathrm{c}},\varphi )=\varepsilon L_{\mathrm{s}}({x}_\mathrm{c},\varphi )/2+{\mathcal {O}}(\varepsilon ^2), \end{aligned}$$
(17)

which simplifies Eq. (14) for small \(\varepsilon\) to

$$\begin{aligned} \hat{{P}}({x}_{\mathrm{c}})&=\frac{\varepsilon }{{2C'}}\int _0^{2\pi }L_\mathrm{s}({x}_\mathrm{c},\varphi )d\varphi =\frac{1}{{{\hat{C}}}}\int _0^{2\pi }L_\mathrm{s}({x}_{\mathrm{c}},\varphi )d\varphi \end{aligned}$$
(18)

with \({\hat{C}}\), according to Eq. (2), such that \(\hat{{P}}({x}_{\mathrm{c}})\) is normalised on the modelling domain \(\Omega _{\mathrm{c}}\), i.e.

$$\begin{aligned} {\hat{C}}&=\int _{\Omega _{\mathrm{c}}}\int _0^{2\pi }L_{\mathrm{s}}({x}_\mathrm{c},\varphi )d\varphi d\Omega _{\mathrm{c}}. \end{aligned}$$
(19)
Fig. 4
figure 4

Deviations from homogeneity and isotropy for straight fibre networks generated by square seeding. a Inhomogeneous fibre density distribution obtained analytically. b Comparison of fibre density obtained by Monte Carlo simulations (\(N=2 \times 10^6\)) and analytic calculations with the homogeneous case. c Error \(e_{\mathrm{i}}\) in isotropic fibre orientation distribution obtained analytically. d Comparison of the error in orientation distribution obtained by Monte Carlo simulations (\(N=2 \times 10^6\)) and analytic calculations with the isotropic case. (ef) Fibre orientation distribution at e the origin O (\({x}_\mathrm{c}=[0,0]\)) and f close to a corner at Q (\({x}_\mathrm{c}=[0.48,0.48]\)) calculated by the analytic approach (black line), by Monte Carlo simulations (blue bars, \(N=2 \times 10^6\)) and compared to the ideal isotropic case (red line)

Full size image

2.5 Fibre orientation distribution for straight fibres

The fibre orientation distribution was evaluated on a circle with diameter \(\varepsilon\) (Fig. 3). As derived for the network density, the orientation distributions \(p({x}_\mathrm{c},\varphi )\) of fibres crossing the circle at \({x}_{\mathrm{c}}\) is given in Eq. (15). By evaluating the integral (16) and making use of the according Taylor expansion (17), the normalised form \({\hat{p}}({x}_{\mathrm{c}},\varphi )\) simplifies for small \(\varepsilon\) to

$$\begin{aligned} {\hat{p}}({x}_{\mathrm{c}},\varphi )&=\frac{1}{{\hat{c}}({x}_{\mathrm{c}})}L_\mathrm{s}({x}_{\mathrm{c}},\varphi ) \end{aligned}$$
(20)

with

$$\begin{aligned} {\hat{c}}({x}_{\mathrm{c}})&=\frac{1}{2\pi }\int _0^{2\pi } L_{\mathrm{s}}({x}_\mathrm{c},\varphi )d\varphi , \end{aligned}$$
(21)

revealing that the fibre orientation distribution is directly proportional to the distance \(L_{\mathrm{s}}\) of the point \({x}_{\mathrm{c}}\) from the boundary \(\partial \Omega _{\mathrm{s}}\) of the seeding domain \(\Omega _{\mathrm{s}}\) in the direction specified by \(\varphi\), cf.  Fig. 3.

2.6 Monte Carlo simulations

In addition to the analytic considerations for straight fibres presented in Secs. 2.4, 2.5, Monte Carlo simulations were conducted. To this end, N fibres were generated and distributed according to the different seeding algorithms with Matlab (R2016b, The MathWorks Inc., Natick, MA, USA).

The fibre density was extracted by counting the number of fibres \(N^{\mathrm{MC}}\) crossing \(N_{\mathrm{c}}=15\) circles with diameter \(\varepsilon =0.04\) equally distributed on a line A spanning from the origin to one of the corners of the square modelling domain (Fig. 1b). These values were normalised, so that

$$\begin{aligned} \hat{{P}}^{\mathrm{MC}}=\frac{N^{\mathrm{MC}}}{{\hat{C}}^{\mathrm{MC}}}, \end{aligned}$$
(22)

where the factor \({\hat{C}}^{\mathrm{MC}}\) was calculated by means of the trapezoidal rule as numerical integration of the discrete values \(N^{\mathrm{MC}}_k\)

$$\begin{aligned} C^{\mathrm{MC}}=\frac{1}{2N_{\mathrm{c}}}\sum _{k=1}^{N_{\mathrm{c}}-1}(N_{k}^\mathrm{MC}+N_{k+1}^{\mathrm{MC}}). \end{aligned}$$
(23)

The global error in homogeneity was calculated according to Eq. (6) as

$$\begin{aligned} E_{\mathrm{h}}=\max _{\text {A}}(|\hat{{P}}^{\mathrm{MC}} - 1|), \end{aligned}$$
(24)

i.e. the maximum value obtained along A. We note that the number of circles \(N_{\mathrm{c}}=15\) was chosen large enough to adequately capture the change of density along A. In general, an arbitrary number can be chosen, but the normalising factor \(C^{\mathrm{MC}}\) (23) obtained by integration becomes more accurate with increasing \(N_{\mathrm{c}}\).

Fig. 5
figure 5

Fibre orientation distributions. Orientation distribution at a the centre O of \(\Omega _{\mathrm{c}}\) \(({x}_\mathrm{c})=[0,0]\) and b close to a corner in point Q \(({x}_\mathrm{c})=[0.48,0.48]\) obtained by extended square seeding with an area ratio of \(\bar{\Omega }_{\mathrm{s}}=28.3\)

Full size image

The orientation distribution was extracted by evaluating the orientation of the fibres crossing the \(N_{\mathrm{c}}=15\) circles equally distributed on the line A (Fig. 1b). For each circle \(k=1,2,\ldots ,N_{\mathrm{c}}\) a histogram with n bins and an according bin width \(w=2\pi /n\) specified by Sturges’ rule [37] was generated. The bin values \(v_i=c_i/c^{\mathrm{MC}}\) were calculated by normalising the bin counts \(c_i\) ensuring a unit value in the isotropic case \(c^\mathrm{MC}=n^{-1}\sum _i^n c_i\). The local error in the orientation distribution was calculated from the values of the normalised histogram according to Eq. (7) as

$$\begin{aligned} e^{\mathrm{MC}}_i({x}_{\mathrm{s}})=\frac{w}{2\pi }\sum _{i=1}^n |v_i({x}_\mathrm{s})-1|, \end{aligned}$$
(25)

and the normalised bin counts \(v_i\) were considered as the discrete values of the computed orientation distribution \({\hat{p}}^{\mathrm{MC}}\). The global error in isotropy was defined as the maximal local error along A

$$\begin{aligned} E_{\mathrm{i}}=\max _A(e^{\mathrm{MC}}_{\mathrm{i}}({x}_{\mathrm{c}})) \end{aligned}$$
(26)

in analogy with the analytical considerations (Eq. (8)).

3 Results

3.1 Deterministic straight fibres

For the computational generation of network structures, straight fibres [27, 38] are often used as simplified base elements and are distributed on \(\Omega _{\mathrm{c}}\). In the following, the influence of the seeding algorithm on the randomness of the final network within \(\Omega _{\mathrm{c}}\) is investigated analytically and by Monte Carlo simulations.

Fig. 6
figure 6

Extended circular seeding a Illustration of seeding \(\Omega _{\mathrm{s}}\) and modelling \(\Omega _{\mathrm{c}}\) domain in the extended circular seeding algorithm with an area ratio of \(\bar{\Omega }_{\mathrm{s}}=10\). b Corresponding fibre density distribution \({\hat{P}}(x_{\mathrm{c}})\) in the modelling domain for a network generated with the extended circular seeding algorithm

Full size image

3.1.1 Square seeding

The fibre density \({\hat{P}}({x}_{\mathrm{c}})\) obtained analytically reveals an inhomogeneous distribution for the square seeding approach (Fig. 4a, b). A comparison with the fibre density obtained by Monte Carlo simulations \(\hat{{P}}^\mathrm{MC}~(N=2\times 10^6)\) shows excellent agreement (Fig. 4b).

The local error in isotropy \(e_{\mathrm{i}}({x}_{\mathrm{c}})\) for the square seeding of straight fibres reveals that the orientation distribution is not constant over \(\Omega _{\mathrm{c}}\) (Fig. 4c, d), i.e. that the networks are anisotropic. Comparison to the local error obtained by Monte Carlo simulations \(e_{\mathrm{i}}^\mathrm{MC}({x}_{\mathrm{c}})\) (\(N=2 \times 10^6\)) again shows accurate agreement (Fig. 4d). A visualization of the orientation distribution of the square modelling domain at the centre O (\({x}_{\mathrm{c}}=[0,0]\)) and close to a vertex at point Q (\({x}_\mathrm{c}=[0.48,0.48]\)) (Fig. 4c) illustrates the deviation of the orientation distribution from the isotropic case (red circle) at both points (Fig. 4e, f). Evaluating the global errors in density (\(E_{\mathrm{h}}=42\%\)) and isotropy (\(E_{\mathrm{i}}=88\%\)) quantifies the substantial difference of the network from the ideal random case.

Fig. 7
figure 7

Errors in homogeneity and isotropy. Errors in homogeneous fibre density (\(E_{\mathrm{h}}\)) and isotropic fibre orientation distribution (\(E_{\mathrm{i}}\)) for different ratios \(\bar{\Omega }_{\mathrm{s}}\) between seeding and modelling domain obtained with the extended square and circular seeding algorithms, respectively

Full size image

3.1.2 Extended square seeding

The extended square seeding uses a concentric square seeding domain \(\Omega _{\mathrm{s}}\) larger than the modelling domain \(\Omega _\mathrm{s}>\Omega _{\mathrm{c}}\). The error in homogeneous density \(E_{\mathrm{h}}\) is decreasing and converging to zero for an increasing area ratio \(\bar{\Omega }_{\mathrm{s}}=|\Omega _{\mathrm{s}}|/|\Omega _{\mathrm{c}}|\) (Fig. 7). For large \(\bar{\Omega }_{\mathrm{s}}\), the decrease of \(E_{\mathrm{h}}\) is proportional to the reciprocal of the area ratio (\(E_{\mathrm{h}}\propto \bar{\Omega }_{\mathrm{s}}^{-1}\)). Interestingly, the error in isotropy \(E_{\mathrm{i}}\) is not converging towards zero with increasing area \(\bar{\Omega }_{\mathrm{s}}\) (Fig. 7). The reason for this is that the distance \(L_{\mathrm{s}}({x}_{\mathrm{c}},\varphi )\) of a point \({x}_{\mathrm{c}}\) to the edge of the seeding domain will always be dependent on the orientation \(\varphi\) in case of a square seeding domain, thus leading to anisotropy, i.e. a non-uniform orientation distribution in the modelling area \(\Omega _{\mathrm{c}}\) also for high ratios \(\bar{\Omega }_{\mathrm{s}}\). This is visualised in Fig. 5 showing the deviation of the orientation distribution of fibres for a large square seeding domain (\(\bar{\Omega }_{\mathrm{s}}=28.3\)) at the centre (point O, \({x}_\mathrm{c}=[0,0]\)) and close to a corner (point Q, \({x}_\mathrm{c}=[0.48,0.48]\)) of \(\Omega _{\mathrm{c}}\).

3.1.3 Extended circular seeding

For the computational generation of random networks with homogeneous fibre density and isotropic fibre orientation in the network a circular seeding domain larger than the square domain of interest \(\Omega _{\mathrm{c}}\) is proposed (Fig. 6a). Evaluating the fibre density by Eq. (18) for \(\Omega _{\mathrm{s}}\) ten times larger than \(\Omega _{\mathrm{s}}\) (\(\bar{\Omega }_{\mathrm{s}}=10\), Fig. 6a) shows a fairly homogeneous distribution (Fig. 6b), particularly when compared to a network generated with the square seeding algorithm (\(\bar{\Omega }_{\mathrm{s}}=1\), Fig. 4a). The representation of the global errors in homogeneity \(E_{\mathrm{h}}\) and isotropy \(E_{\mathrm{h}}\) against the area ratio \(\bar{\Omega }_{\mathrm{s}}\) reveals a decrease with increasing circular seeding domain and a reduction to less than 10% for a ratio \(\bar{\Omega }_{\mathrm{s}}>3.5\) (Fig. 7). For large \(\bar{\Omega }_{\mathrm{s}}\), proportionality to the reciprocal of the area ratio (\(E_{\mathrm{h}}\propto \bar{\Omega }_{\mathrm{s}}^{-1}\)) is achieved.

3.2 Non-deterministic tortuous fibres

Most real networks do not consist of straight but tortuous fibres. A possibility to model this kind of fibres is a random walk which can be parametrised by the persistence length (see Sec. 2.3). In the following, the influence of the seeding domain \(\Omega _{\mathrm{s}}\) on the randomness of the final network in the modelling domain \(\Omega _{\mathrm{c}}\) is investigated by Monte Carlo simulations.

3.2.1 Square seeding

Here, the square seeding algorithm, sampling pivot points only in the modelling domain \(\Omega _{\mathrm{c}}=\Omega _{\mathrm{s}}\) is used to distribute tortuous fibres with persistence length (\(\ell =0.1\)). The final network is plotted for \(N=1\times 10^3\) fibres in Fig. 8a. The fibre density at line A (Fig. 8a) is visualised by evaluating \(N=6\times 10^4\) fibres crossing \(N=15\) circles equally distributed along A. Fig. 8b, c shows a significant error (\(E_{\mathrm{h}}=70\%\)) in the homogeneity of the fibre density, revealing the limited applicability of the square seeding algorithm for tortuous fibres to generate random networks.

Fig. 8
figure 8

Tortuous-fibre networks. a Network consisting of \(N=1\times 10^3\) tortuous (\(\ell =0.1\)) fibres generated with the random seeding algorithm. b Normalised fibre density along line A in a network generated with the square seeding (\({\bar{\Omega }}_{\mathrm{s}}=1\)) and the extended circular seeding (\({\bar{\Omega }}_{\mathrm{s}}=28.3\)) algorithm for tortuous fibres (\(\ell =0.1\), \(N=6\times 10^4\)). c Normalised fibre density in the modelling domain \(\Omega _{\mathrm{c}}\) generated with the square seeding (\({\bar{\Omega }}_{\mathrm{s}}=1\))

Full size image
Fig. 9
figure 9

Density distribution for tortuous-fibre networks generated through extended circular seeding. a Normalised fibre density along A and b fibre orientation distribution at \({x}_{\mathrm{c}}=[0.48,0.48]\) for a network generated with the extended circular seeding algorithm (\(\bar{\Omega }_\mathrm{s}=28.3\), \(N=5\times 10^4\)) for tortuous fibres (\(\ell =0.1\))

Full size image

3.2.2 Extended circular seeding

The extended circular seeding algorithm was used as an alternative to square seeding to generate fibre networks of tortuous fibres. For a seeding to modelling area ratio of \(\bar{\Omega }_{\mathrm{s}}=28.3\) \(N=5 \times 10^4\) fibres where generated and distributed. Fig. 9 shows the fibre density \({\hat{P}}^{\mathrm{MC}}\) along the line A (Fig. 8a) and the orientation distribution \({\hat{p}}^{\mathrm{MC}}\), i.e. the normalised bin counts \(v_i\) (see Sec. 2.6) of fibres crossing a circle (\(\varepsilon =0.04\)) at the point Q (\({x}_{\mathrm{c}}=[0.48,0.48]\)) for a network of highly tortuous fibres (\(\ell =0.1\)). Both \({\hat{P}}^{\mathrm{MC}}\) and \({\hat{p}}^{\mathrm{MC}}\) differ only moderately from the constant values characterising a homogeneous fibre density and isotropic orientation distribution (\(E_{\mathrm{h}}=5.23\%\), \(E_{\mathrm{i}}=3.61\%\)). As a next step the persistence length was varied to represent fibres ranging from highly tortuous (\(\ell =0.1\)) to nearly straight (\(\ell =2.15\)) shapes and to investigate the influence of the tortuosity on the desired homogeneity and isotropy. The results (Fig. 10) reveal that a ratio of \(\bar{\Omega }_{\mathrm{s}}=10\) is sufficient for highly tortuous fibres (\(\ell =0.1\)) to generate networks with a deviation \(E_{\mathrm{h}}\) from the homogeneous case of less than \(10\%\). For increasing persistence lengths the required area ratio reduces to the solution obtained analytically for straight fibres (Fig. 10—grey solid line). The ratio \(\bar{\Omega }_{\mathrm{s}}=10\) also leads to an error \(E_{\mathrm{i}}\) below 10% in the fibre orientation distribution for the whole range of tortuosities (\(\ell =0.1\ldots 2.15\)) making this ratio applicable to achieve networks with acceptable deviations from randomness (\(E_{\mathrm{h}}<10\%\), \(E_{\mathrm{i}}<10\%\)).

Fig. 10
figure 10

Effect of the seeding domain size. Error in the homogeneous fibre density \(E_{\mathrm{h}}\) a and isotropic orientation distribution \(E_{\mathrm{i}}\) b obtained with the extended circular seeding algorithm for different fibre persistence lengths \(\ell\) and different ratios between \(\Omega _{\mathrm{s}}\) and \(\Omega _{\mathrm{c}}\)

Full size image

4 Discussion

In this work, a random network was defined as a structure with a homogeneous fibre density and isotropic fibre orientation distribution. Evidently, a network consisting of a finite number of fibres of finite dimensions can never be point-wise homogeneous and isotropic due to the discrete, i.e. non-continuous nature. However, the local deviations from the ideal case should not correlate with the location within the network, but again, be random. Therefore, we considered the limit case where the number of fibres becomes infinite for the analytical model, and we evaluated the density and isotropy for a small neighbourhood area of a point in Monte Carlo simulations, and we investigated how these characteristics change within the network. For the case of straight fibres, we have shown that the fibre density and orientation distribution derived from the theoretical limit case of an infinite amount of fibres excellently agrees with the average of a finite amount of fibres investigated with Monte Carlo simulations averaged over small circular areas around the respective points.

By means of these methods, we have studied the effect of the size and shape of the seeding domain on homogeneity and isotropy of networks with very long fibres that span the entire seeding domain, i.e. that enter and leave \(\Omega _{\mathrm{s}}\) at its boundary \(\partial \Omega _{\mathrm{s}}\). This type of network is of relevance for the computer-aided analysis of different materials that consist of fibres much longer than the dimensions of the modelling domain, which are restricted by the need for computational efficiency. Electrospun networks or glass wool [2, 8] represent typical examples of such materials. Although not analysed in the present work, straightforward considerations suggest that the size of the seeding domain that can affect the modelling domain decreases with fibre length, since fibres starting sufficiently far away cannot enter \(\Omega _{\mathrm{c}}\) due to their finite length. Accordingly, the problems of heterogeneity and isotropy reported here also exist for shorter fibres, but they might be overcome by choosing an appropriate finite ratio \({\bar{\Omega }}_{\mathrm{s}}\) even for a square shaped seeding domain. In contrast to this, we have shown that the (extended) square seeding will always lead to anisotropic networks for straight fibres of infinite length (Fig. 7). In fact, due to the proportionality of the orientation distribution at point \(x_{\mathrm{c}}\) to its distance \(L_{\mathrm{s}}( x_{\mathrm{c}},\varphi )\) from the boundary of the seeding domain \(\Omega _{\mathrm{s}}\) (Eq. (20)), it is generally impossible to obtain a constant orientation distribution independent of \(\varphi\) within the entire seeding domain. If the centre of the seeding domain lies within \(\Omega _\mathrm{c}\), the orientation distribution in this point inherits the shape of the boundary of \(\Omega _{\mathrm{s}}\), as exemplified for the square shaped \(\Omega _{\mathrm{s}}\) in Fig. 4e. Consequently, in the limit case considered by the analytic model, isotropy can only be obtained in one single point of \(\Omega _{\mathrm{c}}\) that coincides with the centre of a circular seeding domain.

Nevertheless, our results suggest that through the use of an extended circular seeding domain centred within \(\Omega _{\mathrm{c}}\), reasonably random networks of both straight and tortuous fibres can be generated and used for computational studies, and we have shown that for straight fibres the errors in both homogeneity and isotropy reduce proportional to \(\bar{\Omega }_{\mathrm{s}}^{-1}\).

For straight fibres another method was proposed to generate random networks based on \(\mu\)-randomness [39, 40], that makes use of a polar seeding algorithm. Briefly, seeding points are distributed on a circular domain with radius R by sampling its polar coordinates \(\varrho\) and angle \(\vartheta\), with respect to a coordinate system centered at the origin, so that \(\varrho \sim \text {Uni}(0,R), \vartheta \sim \text {Uni}(0,2\pi )\) [41]. The fibres are oriented at their seeding points perpendicular to the connection line from the origin to their corresponding seeds [41]. We implemented and tested this method based on Monte Carlo simulations with \(N=12 \times 10^4\) fibres, and using the same methods to quantify the errors in homogeneity and isotropy along a line A as described in Sec. 2.6. Based on this, we found that polar seeding provides small errors in isotropy for both straight fibres (\(E_\mathrm{i}=6\%\)) and tortuous fibres with \(\ell =0.1\) (\(E_{\mathrm{i}}=3\%\)). The error in homogeneity was also small for straight fibres (\(E_\mathrm{h}=6\%\)), but for tortuous fibres inhomogeneity is clearly observed (Fig. 11) with correspondingly large errors (\(E_{\mathrm{i}}=62\%\)), suggesting that this method overcomes the problem of undesired anisotropy but cannot remedy the heterogeneity.

Fig. 11
figure 11

Density distribution for polar seeding. Normalised fibre density for a network generated with the polar seeding algorithm for straight (\(\ell =\infty\)) and tortuous fibres (\(\ell =0.1\))

Full size image

Finally, we critically remark on a few limitations of the study. To evaluate homogeneity and isotropy in Monte Carlo simulations a large, but clearly finite, number of fibres, a fixed circle diameter \(\varepsilon\) and a given number of angular bins was used. Each realisation of the network is subject to a statistical variation, and when the corresponding statistical variations in density and orientation become larger than those caused by a modification of \({\bar{\Omega }}_{\mathrm{s}}\), the effect of the latter is hidden. This is observed in Fig. 10, where the Monte Carlo simulations do not indicate a reduction of the errors for \({\bar{\Omega }}_{\mathrm{s}}>10\) (Fig. 10a) and \({\bar{\Omega }}_{\mathrm{s}}>10^{0.6}\) (Fig. 10b), respectively. The instance \({\bar{\Omega }}_{\mathrm{s}}\) at which this effect occurs depends on the number N of sampled fibres and can thus be postponed to larger ratios by increasing N. In the present study, we selected 10% as an upper bound for acceptable errors, which is reached already for values of \({\bar{\Omega }}_{\mathrm{s}}\) for which the effect of statistical variations is still small. The number of fibres used for the studies (\(N>12 \times 10^4\)) was further validated by repeated tests with half the number of fibres (Fig. 10). Since the observed influence on the determined errors with values in the range of interest (\(E>10\%\)) was negligible, the initially chosen number of fibres was considered sufficient. Additionally, we note that in Monte Carlo studies homogeneity and isotropy are evaluated only along the diagonal A (Fig. 4) for computational efficiency. For straight fibres (Fig. 4) the results from both the Monte Carlo simulations and analytical model indicated that the locations of the maximal errors in both homogeneity and isotropy fall on the line A, connecting the centre with a vertex of the square modelling domain. For this reason, the same locations were investigated for tortuous fibres.

5 Conclusions

In this contribution, different algorithms were assessed with regard to their capability to generate random planar networks of very long fibers in terms of an even distribution, i.e. homogeneous density of fibres, and isotropic fibre orientation distribution throughout the modelling domain \(\Omega _{\mathrm{c}}\). The square seeding algorithm, distributing seed points uniformly on \(\Omega _{\mathrm{c}}\), leads to significant deviations from randomness for both straight and tortuous fibres, as shown by analytic and Monte Carlo studies. A homogeneous density distribution of straight fibres can be achieved by an increased square seeding domain \(\Omega _{\mathrm{s}}\) but the orientation distribution at any point in \(\Omega _{\mathrm{c}}\) generally remains anisotropic, independent of the size of \(\Omega _{\mathrm{s}}\), and does not converge to the isotropic case for non-circular seeding domains. The proposed use of an extended circular seeding domain reduces the errors in both homogeneity and isotropy with increasing ratio between seeding and modelling domain for straight and tortuous fibres. For straight fibres, the analytical model reveals that the errors in both homogeneity and isotropy scale with \((\Omega _\mathrm{s}/\Omega _{\mathrm{c}})^{-1}\). Given the relative ease at which extended circular seeding domains can be implemented instead of square ones, their use is highly recommended.