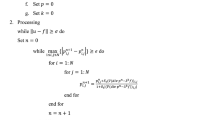Macroscopic examination of welds: Interlaboratory comparison of nominal data

Abstract

A statistical technique is developed for interlaboratory comparisons of the macroscopic examination of weld imperfections caused by failures in the welding process. This technique allows comparisons of nominal data with more than two categories which are influenced by two factors (variables). The development is based on two-way categorical analysis of variation (CATANOVA). Decomposition of the between-laboratory variation for a cross-balanced design by these two factors (e.g., laboratory and technician experience) and their interaction, as well as by the categories of the response variable, is proposed. The developed technique was applied to an interlaboratory comparison using 12 images/photographs of welds with five categories of imperfections as the test items for macroscopic examination. The items were distributed to three participating laboratories and examined by both experienced technicians and novices. Analysis of the obtained data showed a consensus between laboratories and between technicians and no interaction between them. It was found also which categories of imperfections were more difficult to identify than others. This technique is applicable for other nominal properties, and can be adjusted for proficiency testing (PT) of laboratories participated in the comparison.

1 Introduction

An interlaboratory comparison involves the organization, performance and evaluation of measurements or tests on the same or similar items by two or more laboratories in accordance with predetermined conditions. This comparison is used, in particular, for PT of accredited laboratories, as well as laboratories preparing for accreditation [1]. The international standard of general requirements for PT [2] defines qualitative PT schemes as the evaluation of the performance of participating laboratories against established criteria by means of interlaboratory comparisons, where the objective is to identify or describe one or more nominal and ordinal properties or characteristics of the test item in question. For example, the established criteria may consist in a consensus of the results obtained in the participating laboratories. The nominal property value of a phenomenon, body or substance is a word or alphanumerical code given for identification reasons, where the property has no magnitude (e.g., blood groups, colors, or weld imperfections) [3]. Nominal variables are coded by exhaustive and disjoint classes or categories with no natural ordering. Therefore, nominal data are related to categorical data [4, 5]. According to Stevens’ scales of measurement [6], the only legitimate operations between any two nominal variables are equality or nonequality (=, ≠).

The statistical methods recommended for use in PT by interlaboratory comparisons [7] relate to statistical design, value assignment, performance evaluation and scoring for continuous-valued PT schemes. They are not applicable to qualitative nominal data. To date, there are no widely accepted procedures for statistical treatment of nominal data, which can lead to misunderstanding and illogical test result interpretation of nominal properties in a laboratory. This problem is recognized by international groups, such as ISO REMCO [8, 9], ISO TC69 SC 6 [10] and Eurachem/CITAC [11], which work on developing the corresponding guidelines.

The first statistical method for treatment of nominal values similar to one-way analysis of variance ANOVA for quantitative data, was most likely developed in the previous century [12] and re-labeled CATANOVA. Furthermore, CATANOVA was generalized for multidimensional contingency tables [13].

Earlier we studied the case of interlaboratory comparisons for a binary nominal property, i.e. with the number of categories K = 2 , using one-way ordinal analysis of variation ORDANOVA, a methodology applicable to both binary nominal and ordinal (semi-quantitative) properties [14, 15]. Ordinal quantities are also related to categorical data. Ordinal data are defined as values for which a total ordering relation can be established, according to magnitude, with other quantities of the same kind, but for which no algebraic operations exist among those quantities [3]. Their legitimate operations can be “equal/unequal” and “greater/less than” (=,  ≠ ,  > , <) [6]. Examples of such relations are the Mohs hardness of minerals, octane numbers of petroleum fuels and colors of dipsticks for urine tests. One-way ORDANOVA was described thoroughly in papers [16, 17]. The study of binary properties is continued, particularly for analysis of collaborative (interlaboratory) results [18] and for PT [19]. A unifying approach for all the scales of measurement, including both nominal and ordinal (categorical) scales, one-way CATANOVA and one-way ORDANOVA, was proposed in ref. [20].

The aim of the present paper is to develop a statistical technique for interlaboratory comparisons of nominal data with K > 2 categories, influenced by two variables, applicable to macroscopic examination of weld imperfections caused by failures in the welding process, which could be adjusted for PT. As an example, an interlaboratory comparison of the examination results of the imperfections with K = 5 categories (classes according to ISO 17639 [21]) is analyzed. This comparison was organized in 2019 in Croatia by the Mechanical and Metallographic Laboratory, ZIT Ltd. [22], which used macroscopic photographs of cross-sections of different welded joints as the test items (artifacts). The same photographs were distributed simultaneously to the three participating laboratories (factor X1) and examined visually by experienced technicians as well as by novices (factor X2). Important is that there is no any hierarchy of the categories and/or hierarchy of the factors.

The applied interlaboratory comparison scheme is a qualitative, simultaneous, single occasional exercise of data transformation and interpretation by ISO 17043 [2, Sect. 3.7]. Note that the scheme is possible for any number of participating laboratories equal to or more than two [2, Sect. 3.4]. However, the small number of participating laboratories leads to problems in the interpretation of quantitative results, requiring relevant mathematical and metrological solutions [7, 23]. The same is also true for nominal data.

Since the test items in the present study are not samples of a substance, material or a thing but are identical images, there is no question about their chemical or physical homogeneity. The assign value of the testing property and its uncertainty are not objectives in this study, as well as a score of a laboratory proficiency based on a deviation of the laboratory results from the assigned value, required from a PT provider [2, Sect. 4.4.1.3r] for mostly quantitative interlaboratory comparisons. The consensus only of the comparison participants examined the photographs is discussed here, and a laboratory proficiency is considered to be satisfactory when its examination results are in this consensus. Therefore, such a PT is similar to an interlaboratory comparison for evaluation of reproducibility of a test or measurement method.

2 Statistical technique for interlaboratory comparisons of nominal data with K > 2 categories, influenced by two factors

2.1 Description of the nominal data

Assume that the test item examination results [24] are classified according to a nominal scale with K categories (classes) for the response variable Y. The response variability is explained by the influence of two factors—random variables, X1 and X2 , and their possible interaction, X1 ∗ X2. Variable X1 indicates that I laboratories participated in the comparison, i.e., X1 has I levels. Variable X2 has J levels, which may be, for example, the different experience of the technicians, methods of examination used, or type of equipment. There is no any hierarchy of the K categories and/or hierarchy of the factors/variables X1 and X2. When X2 has only one level (J = 1), the two-way model is simplified to the form used in one-way CATANOVA. The total N examination results with K categories of Y are systemized into a cross-layout of I × J cells. Let n_ijk denote the number of results for the k-th category obtained at the i-th laboratory (at the i-th level of X1) and at the j-th level of X2 (e.g., by a technician having the j-th experience level). Thus, n_ij. is the number of examination results in cell (i, j) $\left({\sum}_{k=1}^K{n}_{\mathbf{ijk}}={n}_{\mathbf{ij.}},{\sum}_{i=1}^I{\sum}_{j=1}^J{n}_{\mathbf{ij.}}=N\right)$.

Let ${\hat{p}}_{\mathbf{ijk}}={n}_{\mathbf{ijk}}/{n}_{\mathbf{ij.}}$ denote the proportion of examination results in cell (i, j) belonging to the k-th category $\left({\sum}_{k=1}^K{\hat{p}}_{\mathbf{ijk}}=1\right)$. The value n_..k denote the total number of examination results belonging to the k-th category in the comparison, and ${\hat{p}}_{..\mathbf{k}}={n}_{..\mathbf{k}}/N$ represent the proportion of data belonging to the k-th category $\left({\sum}_{k=1}^K{\hat{p}}_{..\mathbf{k}}=1\right)$. The proportion of data in the (i, j)-th cell is nonrandom and is given by π_ij. = n_ij./N , where ${\sum}_{i=1}^I{\sum}_{j=1}^J{\pi}_{\mathbf{ij.}}=1$.

A detailed description of the model of the examination results and their multinomial distribution is available in the Appendix of this paper.

2.2 Analysis of the nominal data variation

The total sample variation of the response variable Y, normalized to the [0,1] interval, is defined in two-way CATANOVA as

$${\hat{V}}_T=\frac{K}{K-1}\left(1-\sum \limits_{k=1}^K{\hat{p}}_{\ldots {\mathbf{k}}}^2\right).$$

(1)

The total sample variation ${\hat{V}}_T$ is partitioned in ref. [13] into the within (intra) variation ${\hat{V}}_W$ and the between (inter) variation ${\hat{C}}_B$ as follows:

$${\hat{V}}_T={\hat{V}}_W+{\hat{C}}_B,$$

(2)

where

$${\hat{V}}_W=\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\pi}_{\mathbf{ij.}}{\hat{V}}_W^{i\mathbf{j}}=\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\pi}_{\mathbf{ij.}}\frac{K}{K-1}\left(1-\sum \limits_{k=1}^K{\hat{p}}_{\mathbf{ijk}}^2\right)$$

(3)

and

$${\hat{C}}_B=\frac{K}{K-1}\sum \limits_{k=1}^K\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\pi}_{\mathbf{ij.}}{\left({\hat{p}}_{\mathbf{ijk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2.$$

(4)

In the balanced case, when n_ij. = n and π_ij. = 1/IJ, the within and between variations are

$${\hat{V}}_W=\frac{1}{IJ}\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\hat{V}}_W^{i\mathbf{j}}=\frac{1}{IJ}\sum \limits_{i=1}^I\sum \limits_{j=1}^J\frac{K}{K-1}\left(1-\sum \limits_{k=1}^K{\hat{p}}_{\mathbf{ijk}}^2\right)\kern0.5em \mathrm{and}\;{\hat{C}}_B=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{IJ}\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\left({\hat{p}}_{\mathbf{ijk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2.$$

(5)

The multiple influences of the factors X1 and X2 on the response variable Y are characterized by the ratio

$${R}^2=\frac{{\hat{C}}_B}{{\hat{V}}_T},\kern1em 0\le {R}^2\le 1.$$

(6)

This term reflects the joint effect of the factors on Y.

2.3 Decomposition of the between-laboratory variation for a cross-balanced design

In the comparison framework, ${\hat{C}}_B$ characterizes the interlaboratory scattering of the test item examination results as the between-laboratory variation. To evaluate the individual effects of factors X1 and X2, as well as the interaction effect X1 ∗ X2, on the response variable Y, we suggest decomposing ${\hat{C}}_{B}$ into the following parts:

$${\hat{C}}_B={\hat{C}}_{X1}^B+{\hat{C}}_{X2}^B+{\hat{C}}_{X1\ast X2}^B,$$

(7)

where

$${\hat{C}}_{X1}^B=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{I}\sum \limits_{i=1}^I{\left({\hat{p}}_{\mathbf{i.k}}-{\hat{p}}_{..\mathbf{k}}\right)}^2\kern0.5em \mathrm{and}\kern0.5em {\hat{C}}_{X2}^B=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{J}\sum \limits_{j=1}^J{\left({\hat{p}}_{.\mathbf{jk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2,$$

(8)

while

$${\hat{C}}_{X1\ast X2}^B=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{IJ}\sum \limits_{i=1}^I\sum \limits_{j=1}^J{\left({\hat{p}}_{\mathbf{ijk}}-{\hat{p}}_{\mathbf{i.k}}-{\hat{p}}_{.\mathbf{jk}}+{\hat{p}}_{..\mathbf{k}}\right)}^2.$$

(9)

The proposed decomposition allows us to evaluate all the effects separately, including the interaction effect of the factors, using the R² ratios of the components of the between-laboratory variation ${\hat{C}}_B$ by Eqs. (8) and (9) to the total variation ${\hat{V}}_T$ by Eq. (1):

$${R}_{X1}^2=\frac{{\hat{C}}_{X1}^B}{{\hat{V}}_T},\kern1em {R}_{X2}^2=\frac{{\hat{C}}_{X2}^B}{{\hat{V}}_T},\kern0.5em \mathrm{and}\kern0.5em {R}_{X1\ast X2}^2=\frac{{\hat{C}}_{X1\ast X2}^B}{{\hat{V}}_T}.$$

(10)

Another ${\hat{C}}_B$ decomposition, helpful for evaluation of whether the capability of the participating laboratories to identify one category k is better or worse than their capabilities to identify other categories, consists of evaluating the following k-th parts of ${\hat{C}}_B$:

$${\hat{C}}_B(k)=\sum \limits_{i=1}^I\sum \limits_{j=1}^J\frac{1}{IJ}{\left({\hat{p}}_{\mathbf{ijk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2.$$

(11)

The greater ${\hat{C}}_B(k)$ is, the weaker the laboratories’ ability to identify category k is. As mentioned above, when J = 1 (e.g., only one technician in each laboratory participates in the examination of the test items), Eq. (11) is simplified to the form applicable to one-way CATANOVA.

2.4 Testing the null hypothesis on homogeneity of examination results

The null hypothesis of the homogeneity of examination results H₀ states that the probability of identifying a result in the (i, j)-th cell as related to the k-th category (class) does not depend on either i or j, i.e., p_ijk = p_k for all i = 1, 2, …, I and j = 1, 2, …, J. In other words, this hypothesis states that all the laboratories participating in the comparison and their technicians are equivalent in terms of their performance regarding the test item examination. Under this hypothesis, the following relationships are correct:

$$\frac{E\left({\hat{V}}_T\right)}{df_T}=\frac{E\left({\hat{V}}_W\right)}{df_W}=\frac{E\left({\hat{C}}_B\right)}{df_B}=\frac{E\left({\hat{C}}_{X1}^B\right)}{df_{X1}}=\frac{E\left({\hat{C}}_{X2}^B\right)}{df_{X2}}=\frac{E\left({\hat{C}}_{X1\ast X2}^B\right)}{df_{X1\ast X2}}=\frac{\frac{K}{K-1}\left(1-\sum \limits_{k=1}^K{p}_k^2\right)}{N},$$

(12)

where E is the expected value of the random variable, df_T = N − 1, df_W = N − IJ, df_B = IJ − 1, df_X1 = I − 1, df_X2 = J − 1 and df_{X1 ∗ X2} = (I − 1)(J − 1) are the degrees of freedom.

Testing the null hypothesis H₀ requires knowledge of at least one asymptotic distribution of the random variable, allowing us to set the test critical values at the given level of confidence. Light and Margolin [12] for one-way CATANOVA and Anderson and Landis [13] for two-way CATANOVA have shown that the following indicator can be applied for testing:

$$\hat{I}=\left( IJ-1\right)\left(K-1\right){\hat{SP}}_B=\left( IJ-1\right)\left(K-1\right)\frac{{\hat{C}}_B/{df}_B}{{\hat{V}}_T/{df}_T}.$$

(13)

This is because the indicator distribution can be approximated asymptotically by the chi-square distribution ${\chi}_{\left( IJ-1\right)\left(K-1\right)}^2$ with degrees of freedom df = (IJ − 1)(K − 1), while ${\hat{SP}}_B$ is the index of the segregation power.

Note that the approximate asymptotic chi-square distribution of the indicator follows from the multivariate normal distribution and the quadratic forms in normal variables to the multinomial distribution of the examination results. More details are available in the Appendix.

Thus, one can reject H₀ when the indicator $\hat{I}$ exceeds the critical value at the (1 − α) ⋅ 100% level of confidence, i.e., when $\hat{I}>{\chi}_{\left( IJ-1\right)\left(K-1\right)}^2\left(1-\alpha \right)$, and conclude that the joint effect of the factors on the response variable Y is detected. In such cases, the obtained results do not support the equivalence of the examination performance by the participating laboratories or by the different technicians, or both.

In addition, we propose the following three indicators for testing the statistical significance of the factors and their interaction separately. The first indicator

$${\hat{I}}_{X1}=\left(K-1\right)\left(I-1\right){\hat{SP}}_{X1}=\left(K-1\right)\left(I-1\right)\frac{{\hat{C}}_{X1}^B/{df}_{X1}}{{\hat{V}}_T/{df}_T}\sim {\chi}_{\left(K-1\right)\left(I-1\right)}^2$$

(14)

allows us to test the null hypothesis regarding the equivalence of the levels i of factor X1 (p_i.k = p_k), i.e., the equivalence of the examination of the test items at different laboratories when the laboratories have technicians with the same experience and the same equipment. The null hypothesis is rejected when ${\hat{I}}_{X1}>{\chi}_{\left(K-1\right)\left(I-1\right)}^2\left(1-\alpha \right)$. In the case of rejection of the null hypothesis, the interlaboratory comparison task is to show which laboratory is significantly different from the others. If this laboratory is found and removed from the calculation of ${\hat{C}}_{X1}^B$ using Eq. (8), the null hypothesis is not rejected. When the number of laboratories I is large enough, more than one laboratory may have to be removed before the null hypothesis is accepted. Note that the homogeneous results of the rest of the laboratories form a consensus. When the interlaboratory comparison is applied for a PT, proficiency of a laboratory participating in this consensus is considered to be satisfactory. The question remains, however, whether the removed laboratory performed the examination more or less correctly than the rest of the laboratories. This occurs when the test items are not measurement standards and there is no metrological traceability to the International System of Units (SI). Thus, the removed laboratory is not ‘bad’, it is simply not a part of the consensus [25].

The second indicator,

$${\hat{I}}_{X2}=\left(K-1\right)\left(J-1\right){\hat{SP}}_{X2}=\left(K-1\right)\left(J-1\right)\frac{{\hat{C}}_{X2}^B/{df}_{X2}}{{\hat{V}}_T/{df}_T}\sim {\chi}_{\left(K-1\right)\left(J-1\right)}^2,$$

(15)

is helpful for testing the null hypothesis regarding the equivalence of the levels j of factor X2 representing the experience of the technicians or another condition in the laboratories (p_.jk = p_k). The null hypothesis is rejected when ${\hat{I}}_{X2}>{\chi}_{\left(K-1\right)\left(J-1\right)}^2\left(1-\alpha \right)$.

The third indicator,

$${\hat{I}}_{X1\ast X2}=\left(K-1\right)\left(I-1\right)\left(J-1\right){\hat{SP}}_{X1\ast X2}=\left(K-1\right)\left(I-1\right)\left(J-1\right)\frac{{\hat{C}}_{X1\ast X2}^B/{df}_{X1\ast X2}}{{\hat{V}}_T/{df}_T}\sim {\chi}_{\left(K-1\right)\left(I-1\right)\left(J-1\right)}^2$$

(16)

is for testing the null hypothesis regarding the absence of interaction between the levels i of factor X1 and the levels j of factor X2, influencing the examination of the test items in the participating laboratories (p_ijk = p_k). This null hypothesis is rejected when ${\hat{I}}_{X1\ast X2}>{\chi}_{\left(K-1\right)\left(I-1\right)\left(J-1\right)}^2\left(1-\alpha \right)$. The rejection means that the impact of the technicians’ experience or another condition on the examination results depends on the laboratories that participated in the comparison.

Note that the proposed calculations are based on the formulas requiring the simplest mathematical operations and can be performed using a routine Excel sheet.

3 Interlaboratory comparisons of macroscopic examinations of welds

3.1 Design of experiment

The three accredited laboratories that participated in the comparison (denoted L1, L2 and L3) were asked to recognize and classify weld imperfections according to ISO 6520-1 [26]. These imperfections, caused by failures in the welding process, were seen in 12 images/macroscopic photographs—the test items. Table 1 presents the categories/classes of the possible weld imperfections and their designations by macroscopic examination.

Table 1 Classification of features by macroscopic examination

Note that the reference numbers in Table 1 are for labeling the imperfections by standard [26]. These numbers do not influence the definition of the obtained results as nominal (not ordinal) data.

An example from the test items is shown in Fig. 1. The photograph presents the macrostructure (magnification: max. ×10) of a transverse cross-section of a fillet weld from both sides. The welded joint consisted of two plates with a thickness of 10 mm made from the same base material, non-alloyed structural high tensile strength steel S355J2 delivered in the normalized heat treatment condition. The joint was processed by multirun metal active gas welding with a flux core electrode BÖHLER Ti52-FD as a filler material. Before macroscopic photographs were taken for further visual examination, the specimen was subjected to grinding (500 grit) and then etched with 5% nitric acid for a few seconds [27] to ensure that any features in the weld were clearly revealed.

Fig. 1

An example of a test item: a photograph of the macrostructure of a fillet weld from both sides

The same 12 test items (the same 12 macroscopic photographs of different welded joints) were sent to each participating laboratory. Ten items had only one feature (imperfection) to detect, and each of the other two items had two different features. Thus, 14 examination results—classes of weld imperfections—were expected from every participating laboratory.

Laboratory L1 was also interested in comparing the examination results from an experienced technician (A) and a novice (B). The participating laboratory thus provided two datasets (A and B), each containing 14 examination results.

3.2 The examination results

The results from the examination of the test items are presented in Table 2. Laboratories L2 and L3 did not provide datasets for novices (B). To demonstrate the developed statistical technique, exemplificative novice (B) data were added to Table 2 for these two laboratories.

Table 2 Identified classes of weld imperfections

The examination results for the test items are summarized in Table 3. In total, there were N = 84 results from the test item examinations, while the sample size including all technicians and laboratory results was n_ij. = 14.

Table 3 Number of examination results by categories/classes

3.3 Discussion of the obtained results

The total sample variation of the examination results is ${\hat{V}}_T=0.9524$ with df_T = 83 by Eq. (1); the within (intra) laboratory variation is ${\hat{V}}_W=0.9056$ with df_W = 78, and the between- (inter) laboratory variation is ${\hat{C}}_B=0.0468$ with df_B = 5 by Eq. (5). The ratio R² = 0.0491 by Eq. (6) indicates the joint influence of a laboratory and technician experience on the variability of the obtained results, is practically negligible. The test statistic (index of the segregation power) is $\hat{SP_B}=0.8152$ , and the indicator is $\hat{I}=16.30$ by Eq. (13). The critical value of the chi-square distribution at the 95% level of confidence and 20 degrees of freedom is ${\chi}_{(20)}^2(0.95)=31.40$. Thus, there is no rejection of the null hypothesis of homogeneity H₀ at the 95% level of confidence: the laboratories and their technicians do not differ statistically. Additional details obtained using decomposition of the between-laboratory variation ${\hat{C}}_B$ by Eqs. (7)–(9) are given in Table 4, including the R² ratio values from Eq. (10), segregation power indices and indicators from Eqs. (14)–(16), appropriate degrees of freedom of indicators df and critical values of the chi-square distribution χ²(0.95) at the 95% level of confidence.

Table 4 Results of the between-laboratory variation decomposition and parameters for testing H₀ hypotheses on the statistical significance of the variation components

All the variation components are small, but the component related to the laboratory factor is the largest. Nevertheless, the indicators in Table 4 do not exceed the critical chi-square values, and the null hypotheses are not rejected at the 95% level of confidence. Therefore, these statistical tests support the finding that the laboratories’ and technicians’ examination results for weld imperfections do not differ. There is also no statistically significant interaction between the ‘laboratory’ and ‘experience of technician’ as factors. In general, the obtained results show a consensus between laboratories and between technicians, and therefore also acceptable training of novices. Thus, the proficiency of the participants of the comparison can be considered as satisfactory.

Decomposition of the ${\hat{C}}_B$ by categories or classes using Eq. (11) leads to the values

${\hat{C}}_B(1)=0.0126;\kern0.5em {\hat{C}}_B(2)=0.0011;\kern0.5em {\hat{C}}_B(3)=0.0013;\kern0.5em {\hat{C}}_B(4)=0.0109;\kern0.5em {\hat{C}}_B(5)=0.0115.$

This means that the capability of the laboratories to identify weld imperfections is better for classes k = 2 and 3 (cavities and inclusions, respectively) than for the rest of the classes. Cracks (k = 1) , lack of fusion (k = 4) and geometric shape errors (k = 5) are much more difficult to identify.

4 Conclusions

A statistical technique for interlaboratory comparisons of nominal data that are influenced by two factors (variables) was developed based on two-way CATANOVA. The technique includes decomposition of the total variation for a cross-balanced design according to the factors (e.g., laboratory and experience of technician) and their interaction, as well as according to the categories of the response variable.

Application of the developed technique was demonstrated for the interlaboratory comparison of the macroscopic examination of weld imperfections caused by failures in the welding process, with five categories. The comparison was organized using 12 photographs of the macrostructures of the welds as test items distributed to three participating laboratories and examined by experienced technicians, as well as by novices. Analysis of the obtained data showed a consensus between laboratories and between technicians and no interaction between them. Therefore, the proficiency of the participants of the comparison can be considered as satisfactory.

It was found that the weld imperfections from two categories (cavities and inclusions) were examined with low variation, while the examination results of imperfections belonging to the three other categories (cracks, lack of fusion, and geometric shape errors) had significantly larger variations, i.e., were much more difficult to identify.

The proposed calculations are based on the formulas requiring the simplest mathematical operations and can be performed using a routine Excel sheet. The developed technique is applicable for other nominal properties, and can be adjusted for PT of laboratories participated in the comparison.

Appendix: Model of the examination results and their distribution

A weld examination result is a nominal random phenomenon Y (the response variable) characterized by a probability vector p with K categories, i.e.: p = (p₁, p₂, …, p_K), where p_k denote the probability of data belonging to the k-th category $\left({\sum}_{k=1}^K{p}_k=1\right)$. There are K = 5 categories of weld imperfections listed in Table 1 (k = 1, 2, …, 5). We consider the results of interlaboratory comparison of the weld examination results influenced by two independent variables (and possibly their interaction) on the nominal response variable. One of variables X1 denotes the first factor—laboratories which participated in the comparison with I = 3 levels, and the second variable X2 denotes the second factor with J = 2 levels (experienced technician versus a novice one). Assume we have N examination results with K categories of Y, each of them systemized into one of I levels of the first factor X1 and into one of the J levels of the second factor X2. The number of results in the (i, j)-th cell belonging to the k-th category of Y is n_ijk, where the counts n_ijk are random. Thus, the (i, j)-th cell contains ${n}_{\mathbf{ij.}}={\sum}_{k=1}^K{n}_{\mathbf{ijk}}$ examination results, and in total there are ${\sum}_{i=1}^I{\sum}_{j=1}^J{n}_{\mathbf{ij.}}=N$ data. The proportion of data in the (i, j)-th cell is nonrandom and is given by π_ij. = n_ij./N, where ${\sum}_{i=1}^I{\sum}_{J=1}^J{\pi}_{\mathbf{ij.}}=1$.

Let ${\hat{p}}_{\mathbf{ijk}}={n}_{\mathbf{ijk}}/{n}_{\mathbf{ij.}}$ denote the proportion of data belonging to the k-th category in the (i, j)-th cell $\left({\sum}_{k=1}^K{\hat{p}}_{\mathbf{ijk}}=1\right)$. Due to the nature of the counting procedure the random vector (n_ij1, n_ij2, …, n_ijK) follows the multinomial distribution [5] with n_ij. and the probability vector p_ij = (p_ij1, p_ij2, …, p_ijK). That is

$$P\left({n}_{ij1},{n}_{ij2},\dots {n}_{ij K}\right)=\frac{n_{ij.}}{\prod_{k=1}^K{n}_{ij k}!}\prod \limits_{k=1}^K{p}_{ij k}^{n_{ij k}}.$$

Hence, the expected value and variation of the proportion of data belonging to the k-th category in the (i,j)-th cell are

$$E(\hat{p}_{{..k}} ) = E\left( {\frac{{n_{{ijk}} }}{{n_{{\user2{ij}.}} }}} \right) = p_{{ijk}} ,\quad VAR(\hat{p}_{{ijk}} ) = \frac{{p_{{ijk}} (1 - p_{{ijk}} )}}{{n_{{\user2{ij}}} }}.$$

The total number of examination results belonging to the k-th category is denoted by ${n}_{..\mathbf{k}}={\sum}_{i=1}^I{\sum}_{j=1}^J{n}_{\mathbf{ijk}}$, and the counts n_..k are random. The random vector (n_..1, n_..2, …, n_..K) follows the multinomial distribution with N and the probability vector p = (p₁, p₂, …, p_K). Furthermore, ${\hat{p}}_{..\mathbf{k}}={n}_{..\mathbf{k}}/N$ denote the proportion of data belonging to the k-th category $\left({\sum}_{k=1}^K{\hat{p}}_{..\mathbf{k}}=1\right)$.

For the cross-balanced design, we assume that each of the (i, j) cells contains the same amount of examination results, that is n_ij. = n, thus the total amount of examination results equals N = IJn and π_ij. = 1/IJ.

The null hypothesis of homogeneity of the examination results H₀ assumes that all results drawn from the same infinite population are characterized by the probability vector p = (p₁, p₂, …, p_K). This is, identifying an examination result in the (i, j)-th cell as related to the k-th category does not depend on either i or j, i.e., p_ijk = p_k for all i = 1, 2, …, I and j = 1, 2, …, J. Therefore, under the null hypothesis, it follows that

$$E(\hat{p}_{{..k}} ) = E\left( {\frac{{n_{{..k}} }}{N}} \right) = p_{{k,}} \quad VAR(\hat{p}_{{..k}} ) = \frac{{p_{k} (1 - p_{k} )}}{N}.$$

Moreover, we obtain the following:

$${\displaystyle \begin{array}{l}E\left({\hat{p}}_{..k}^2\right)= VAR\left({\hat{p}}_{..k}\right)+{E}^2\left({\hat{p}}_{..k}\right)=\frac{p_k}{N}+\frac{\left(N-1\right){p}_k^2}{N}\\ {}E\left({\hat{p}}_{ijk}^2\right)= VAR\left({\hat{p}}_{ijk}\right)+{E}^2\left({\hat{p}}_{ijk}\right)=\frac{p_k}{N}+\frac{\left(N-1\right){p}_k^2}{n}\end{array}}$$

Under this hypothesis, the relationships shown in Eq. (12) is justified:

$$E\left({\hat{V}}_{\mathrm{T}}\right)=E\left(\frac{K}{K-1}\left(1-\sum \limits_{k=1}^K{\hat{p}}_{..\mathbf{k}}^2\right)\right)=\frac{K}{K-1}\left(1-\sum \limits_{k=1}^KE\left({\hat{p}}_{..\mathbf{k}}^2\right)\right)={df}_{\mathrm{T}}\frac{\frac{K}{K-1}\left(1-{\sum}_{k=1}^K{p}_{\mathbf{k}}^2\right)}{N}$$

where df_T = N − 1. In the same manner, the expected value of the within (intra) variation ${\hat{V}}_W$ is equal to:

$$E\left({\hat{V}}_{\mathrm{W}}\right)=\frac{1}{IJ}\sum \limits_{i=1}^I\sum \limits_{j=1}^J\frac{K}{K-1}\left(1-\sum \limits_{k=1}^KE\left({\hat{p}}_{\mathbf{ijk}}^2\right)\right)={df}_W\frac{\frac{K}{K-1}\left(1-{\sum}_{k=1}^K{p}_{\mathbf{k}}^2\right)}{N},$$

where df_W = nIJ − IJ = N − IJ. The expected value of the between (inter) variation ${\hat{C}}_B$ is equal to

$$E\left({\hat{C}}_{\mathrm{B}}\right)=E\left({\hat{V}}_{\mathrm{T}}\right)-E\left({\hat{V}}_{\mathrm{W}}\right)={df}_B\frac{\frac{K}{K-1}\left(1-{\sum}_{k=1}^K{p}_{\mathbf{k}}^2\right)}{N},$$

where df_B = IJ − 1.

To calculate the expected value of the components that form the between (inter) variation ${\hat{C}}_B$ in Eq. (7), that is ${\hat{C}}_B={\hat{C}}_{X1}^B+{\hat{C}}_{X2}^B+{\hat{C}}_{X1\ast X2}^B$, we set the following. Let ${\hat{p}}_{\mathbf{i.k}}$ denote the proportion of examination results belonging to the k-th category of Y at level i of factor X1 and let ${\hat{p}}_{.\mathbf{jk}}$ denote the proportion of examination results belonging to the k-th category of Y at level j of factor X2. It follows that

$${\displaystyle \begin{array}{l}E\left[{\left({\hat{p}}_{\mathbf{i.k}}-{\hat{p}}_{..\mathbf{k}}\right)}^2\right]=\left(I-1\right)\frac{p_k\left(1-{p}_k\right)}{N}\\ {}E\left[{\left({\hat{p}}_{.\mathbf{jk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2\right]=\left(J-1\right)\frac{p_k\left(1-{p}_k\right)}{N}\end{array}}$$

Therefore,

$$E\left({\hat{C}}_{X1}^{\mathrm{B}}\right)=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{I}\sum \limits_{i=1}^IE\left[{\left({\hat{p}}_{\mathbf{i.k}}-{\hat{p}}_{..\mathbf{k}}\right)}^2\right]={df}_{X1}\frac{\frac{K}{K-1}\left(1-{\sum}_{k=1}^K{p}_{\mathbf{k}}^2\right)}{N},$$

$$E\left({\hat{C}}_{X2}^{\mathrm{B}}\right)=\frac{K}{K-1}\sum \limits_{k=1}^K\frac{1}{J}\sum \limits_{j=1}^JE\left[{\left({\hat{p}}_{.\mathbf{jk}}-{\hat{p}}_{..\mathbf{k}}\right)}^2\right]={df}_{X2}\frac{\frac{K}{K-1}\left(1-{\sum}_{k=1}^K{p}_{\mathbf{k}}^2\right)}{N}.$$

Then, $E\left({\hat{C}}_{X1\ast X2}^{\mathrm{B}}\right)=E\left({\hat{C}}_{\mathrm{B}}\right)-E\left({\hat{C}}_{X1}^{\mathrm{B}}\right)-E\left({\hat{C}}_{X2}^{\mathrm{B}}\right)$, where df_X1 = I − 1, df_X2 = J − 1 and df_{X1 ∗ X2} = (I − 1)(J − 1).