1 Introduction

In open-pit mines, the long-term production scheduling (LTPS) is known as a complex optimization problem that is composed of input data uncertainty, large datasets, and various constraints. Uncertainties in mining projects are arising from inadequate and imperfect data. Different geological, economic, or technical factors subject to uncertainty in the input. The uncertainty caused by geological features is deliberated to be the most significant source of uncertainty among these factors as it is generally termed grade uncertainty. Geostatistical conditional simulation techniques develop a framework to measure grade uncertainty through generating multiple, equally probable simulated recognitions of the orebody. Over the last few years, a large number of models have been proposed to incorporate this grade uncertainty into the optimization process. However, it is generally complicated and computationally costly to solve these models for actual-sized open-pit mines. Over the past few decades, researchers have greatly succeeded in this respect, as shown in Table 1. Accordingly, there has been a more comprehensive discussion on the allocation of optimal algorithms and the future of production planning. Despite the efforts of researchers, it is not possible to consider LTPS problem as a well-solved problem. Because of the advantages of heuristic and metaheuristic algorithms, the usage of these techniques in industries is enhancing [1]. Figure 1 shows the domains of metaheuristic algorithms applications in different fields.

Table 1 A review of a number of models presented in recent years
Full size table
Fig. 1
figure 1

The share of metaheuristic algorithms application in different fields (in percentage)

Full size image

The majority of the metaheuristics have been expanded before the year 2000. These algorithms are named “classical metaheuristic algorithms” in this survey. The aforementioned classical algorithms are genetic algorithms (GA) [2], particle swarm optimization (PSO) [3], ant colony optimization (ACO) [4], genetic programming (GP) [5], differential evolution (DE) [6], simulated annealing (SA) [7], tabu search (TS) [8], greedy randomized adaptive search procedure (GRASP) [9], artificial immune algorithm (AIA) [10], iterated local search (ILS) [11], chaos optimization method (COM) [12], scatter search (SS) [13], shuffled frog-leaping algorithm (SFLA) [14], and variable neighborhood search (VNS) [15].

The new algorithms are named “new generation metaheuristic algorithms” that they are such as artificial bee colony (ABC) [16], bacterial foraging (BFO) [17], bat algorithm (BA) [18], biogeography-based optimization (BFO) [19], cuckoo search (CS) [20], firefly algorithm (FA) [21], gravitational search algorithm (GSA) [22], grey wolf optimizer algorithm (GWO) [23], krill herd (KH) [24], social spider optimization (SSO) [25], symbiotic organisms search (SOS) [26], and whale optimization algorithm (WOA) [27]. The percentage of related studies about optimization for the classical and new generation metaheuristics is presented in Figs. 2 and 3.

Fig. 2
figure 2

The share of related studies about optimization for classical metaheuristics

Full size image
Fig. 3
figure 3

The share of related studies about optimization for new generation metaheuristics

Full size image

In this study, the applications of metaheuristic algorithms have been dissected to solve the LTPS problem in open-pit mines, taking into account uncertainty. Using the hybrid technique by augmented Lagrangian relaxation (ALR) and GWO, the LTPS problem has been elucidated under grade uncertainty condition. Here, the ALR technique is applied to the LTPS problem to improve its performance and thus to speed up the convergence. Likewise, the GWO technique is applied thereon to update the Lagrangian multipliers. The proposed model has been compared with the results of the hybrid methods gained from the classic Lagrangian relaxation (LR) and ALR methods integrated with the BA, PSO, GA, the traditional subgradient method (SG), and conventional method without using the Lagrangian approach (Conv.). The case study with its constraints is evaluated to inspect the efficacy of the proposed method. Actually, the proposed method can be solved LTPS problems in rational time with a high-quality solution.

The subsequent part of this paper is scheduled as below. Sections 2 and 3 indicate the objective functions and their associated constraints. Also, these sections indicate a summary of the methodology and the proposed model will be developed. Section 4 includes an evaluation of the outcomes. The established models are now validated. In Sect. 5, the results are analyzed and discussed. Finally, Sect. 6 shows the deduction.

2 The long-term production scheduling problem formulation under grade uncertainty

During several years, the LTPS has been implemented to assess production purposes and material flow in the ore [28]. It is typically simply represented and developed as a linear problem. To take these decision-making targets, the most straightforward way is to develop a full-space optimization model. Here, in each time period of the scheduling horizon, the availability constraints are incorporated into the model. Equation (1) provides the objective function (OF) of the LTPS problem and Eqs. (2)–(7) display the model constraints.

$$ {\text{Maximize}}\,\,\, Z = \mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{t}^{T} \frac{{NV_{n}^{t} }}{{\left( {1 + r} \right)^{t} }} \times X_{n}^{t} $$
(1)
$$ \mathop \sum \limits_{n = 1}^{N} \left( {g_{n} - G_{\hbox{max} } } \right) \times O_{n} \times X_{n}^{t} \le 0 $$
(2)
$$ \mathop \sum \limits_{n = 1}^{N} \left( {g_{n} - G_{\hbox{min} } } \right) \times O_{n} \times X_{n}^{t} \ge 0 $$
(3)
$$ \mathop \sum \limits_{t = 1}^{T} X_{n}^{t} \le 1 ,\,\,\,\,\forall n = 1,2,3, \ldots ,N $$
(4)
$$ \mathop \sum \limits_{n = 1}^{N} \left( {O_{n} \times X_{n}^{t} } \right) \le {\text{PC}}_{\hbox{max} } $$
(5)
$$ \mathop \sum \limits_{n = 1}^{N} \left( {O_{n} + W_{n} } \right) \times X_{n}^{t} \le {\text{MC}}_{\hbox{max} } $$
(6)
$$ YX_{k}^{t} - \mathop \sum \limits_{y = 1}^{l} \mathop \sum \limits_{r = 1}^{t} X_{y}^{r} \le 0,\,\,\,\forall y = 1,2, \ldots ,l,\,\,\,\forall k = 1,2, \ldots ,N,\,\,\,\forall t = 1,2, \ldots ,T. $$
(7)

The following indications were approved in the model constructed:

  • n: is the block identification number, n = 1, 2, …, N;

  • N is the total number of blocks requiring to be scheduled;

  • t is the index of periods in scheduling horizon, t = 1, 2, …, T;

  • T is the total number of scheduling periods;

  • \( {\text{NV}}_{n }^{t} \) is the net value to be generated if block n is mined in period t;

  • r is the discount rate in each period;

  • \( X_{n }^{t} \) is the binary variable;

  • Gmax is the value of the definite grade;

  • gn is the mean grade of block n and On is the tonnage of ore in block n;

  • PCmax is the processing capacity;

  • MCmax is the mining capacity;

  • Wn is the tonnage of waste material in block n;

  • k is the index of a block regarded as extraction in period t;

  • Y is the total number of blocks that overly block k;

  • y is the counter for the Y-overlying blocks.

At present, the indicator kriging (IK) is one of the most widely used methods for grade estimation in mining projects. This technique was presented by Journel [29] to estimate the resources. The nature of the indicator method is binary data encoding depending on the cutoff value, \( Z_{c} \). For the \( Z\left( x \right) \) value, \( i_{k} \left( x \right) = 1 \) if \( Z\left( x \right) \ge Z_{C} \), and otherwise, \( i_{k} \left( x \right) = 0 \). In fact, it is a nonlinear conversion of data value to binary system [30]. Outcome values between 0 and 1 for each estimation point provide a set of indicators-converted quantity using kriging, that can be expounded as the proportion of the block overhead the determined cutoff on data support and the probability that the grade is overhead the determined indicator [31]. In the optimization procedure of this paper, a mixed-integer programming (MIP) model is proposed to investigate grade uncertainty. In the block model, a possibility is allocated to each block (UIn), indicating the probability of n for each block. Currently, the OF is organized such that earlier production periods are provided to mine higher-certainty blocks. Once extra information is available, uncertain blocks are generally postponed for later periods. Subsequently, another OF is introduced to the OF of the conventional model as follows:

$$ {\text{Maximize}}\,\,\,Z^{\prime} = \mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{t}^{T} \frac{{NV_{n}^{t} }}{{\left( {1 + r} \right)^{t} }} \times UI_{n} \times X_{n}^{t}. $$
(8)

This OF yields constraints (2)–(7).

3 Structure of proposed model

3.1 Using the augmented Lagrangian relaxation strategy for the reformulation of the long-term production scheduling problem

The LR method is regarded as a mathematical tool for MIPs. In introducing this method in LTPS, system constraints are relaxed and introduced to the OF by Lagrangian multipliers [32]. Afterward, the relaxed problem is decomposed into a further controllable subproblem for individual units and solved using dynamic programming [33]. Due to system constraint violations, the subgradient method is used to update multipliers [34]. The main idea of the LR method is system constraint relaxation by Lagrangian multipliers [35]. Then, the relaxed problem is decoupled into separate smaller subproblems [36]. The constant Lagrangian function is formulated by assigning non-negative Lagrangian multipliers λt, μt, and ʋt with respect to processing type in period t [37].

The ALR method has the potential to be used to solve the proposed problem. According to the function introduced by Andreani et al. [38], the ALR method is employed to generate a feasible solution for the original problem effectively. Given the reformulation above, once the coupling constraints (4)–(6) are relaxed, the resulting model (8) can be divided into several subproblems. The original (maximization) OF is on a par with the minimization of a revised OF. Here, the OF has been defined as follows:

$$ {\text{Min }}\,\, Z^{\prime\prime}\left( X \right) = - Z^{\prime}\left( X \right). $$
(9)

Relaxing constraints (4)–(6) yields the following ALR problem:

$$ \begin{aligned} L\left( {X,\lambda , \mu , \upsilon ,\sigma } \right) & = {\text{Min}}\,\, Z^{\prime\prime}\left( X \right) + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {X_{n}^{t} - 1} \right) + \frac{{\lambda^{t} }}{\sigma }} \right)^{2} \\ & \quad + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {O_{n} \times X_{n}^{t} } \right) - {\text{PC}}_{\hbox{max} } + \frac{{\mu^{t} }}{\sigma }} \right)^{2} \\ & \quad + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {O_{n} + W_{n} } \right) \times X_{n}^{t} - {\text{MC}}_{\hbox{max} } + \frac{{\upsilon^{t} }}{\sigma }} \right)^{2}. \\ \end{aligned} $$
(10)

According to the objective function, the formulation can be written as:

$$ \begin{aligned} L\left( {X,\lambda , \mu , \upsilon ,\sigma } \right) & = {\text{Min}} - \mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{t}^{T} \frac{{{\text{NV}}_{n}^{t} }}{{\left( {1 + r} \right)^{t} }} \times {\text{UI}}_{n} \times X_{n}^{t} + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {X_{n}^{t} - 1} \right) + \frac{{\lambda^{t} }}{\sigma }} \right)^{2} \\ & \quad + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {O_{n} \times X_{n}^{t} } \right) - {\text{PC}}_{\hbox{max} } + \frac{{\mu^{t} }}{\sigma }} \right)^{2} \\ & \quad + \frac{\sigma }{2} \times \mathop \sum \limits_{t}^{T} \left( {\left( {O_{n} + W_{n} } \right) \times X_{n}^{t} - {\text{MC}}_{\hbox{max} } + \frac{{\upsilon^{t} }}{\sigma }} \right)^{2}. \\ \end{aligned} $$
(11)

3.2 Lagrangian multipliers updating with the grey wolf optimizer

Given Lagrangian multipliers, they should be adjusted carefully to take advantage of the ALR. Most references to update Lagrangian multipliers utilize the subgradient method and some heuristic methods simultaneously to get a quick solution. Metaheuristic algorithms are considered suitable for solving the predicted problem. This study applies GWO to update Lagrangian multipliers and enhance ALR performance and compared it with the results of using the hybrid methods of LR and ALR with the BA, PSO, GA, and SG.

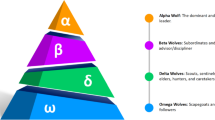
In 2014, Mirjalili et al. [23] presented the GWO based on the social leadership of the grey wolves and their hunting group behavior in nature. As shown in Fig. 4, the group of the grey wolves is divided into alpha (α), beta (β), delta (δ), and omega (ω) in terms of social hierarchy behaviors [39]. Alpha is responsible for making major decisions. Beta, delta, and omega are in the lower ranks of dominance. In fact, according to this novel metaheuristic algorithm, the most appropriate solution considered to alpha and then assumed to beta and delta, respectively [40]. As well as, the remaining solutions belong to omega. The initial appropriate wolves that are closer to the prey are (α), (β) and (δ), which lead the remnant of the group (ω) to search for a prey in promising regions. Chasing, encircling, and attacking prey are the major hunting procedures of wolves [41]. The behavior of grey wolves in prey encircling is formulated as follows [42]:

$$ \vec{D} = \left| {\vec{C} \cdot \overrightarrow {{X_{P} }} \left( t \right) - \vec{X}\left( t \right)} \right| $$
(12)
$$ \vec{X}\left( {t + 1} \right) = \overrightarrow {{X_{P} }} \left( t \right) - \vec{A} \cdot \vec{D}, $$
(13)

where \( \vec{D} \) demonstrates the distance among the grey wolf and the prey, t indicates the number of the current iteration, \( \vec{X} \) shows the grey wolf position vector, and \( \overrightarrow {{X_{P} }} \) is the prey position vector. As well as, \( \vec{A} \) and \( \vec{C} \) are coefficient vectors that computed as follows:

$$ \vec{A} = 2\vec{a} \cdot \overrightarrow {{r_{1} }} - \vec{a} $$
(14)
$$ \vec{C} = 2 \cdot \overrightarrow {{r_{2} }}, $$
(15)

where \( \overrightarrow {{r_{1} }} \), \( \overrightarrow {{r_{2} }} \) indicate random vectors in [0, 1], and the factor of \( \vec{a} \) is linearly reduced from 2 to 0 over the period of iterations.

Fig. 4
figure 4

Hierarchy of grey wolf

Full size image

Hence, the three major solutions obtained are stored, and other search factors update their locations based on the location of ideal search factors. Their locations can be updated by GWO as follows:

$$ \overrightarrow {{D_{\alpha } }} = \left| {\overrightarrow {{C_{1} }} \cdot \overrightarrow {{X_{\alpha } }} - \vec{X}} \right| ,\overrightarrow {{D_{\beta } }} = \left| {\overrightarrow {{C_{2} }} \cdot \overrightarrow {{X_{\beta } }} - \vec{X}} \right| , \overrightarrow {{D_{\delta } }} = \left| {\overrightarrow {{C_{3} }} \cdot \overrightarrow {{X_{\delta } }} - \vec{X}} \right| $$
(16)
$$ \overrightarrow {{X_{1} }} = \overrightarrow {{X_{\alpha } }} - \overrightarrow {{A_{1} }} \cdot \left( {\overrightarrow {{D_{\alpha } }} } \right) , \overrightarrow {{X_{2} }} = \overrightarrow {{X_{\beta } }} - \overrightarrow {{A_{2} }} \cdot \left( {\overrightarrow {{D_{\beta } }} } \right) , \overrightarrow {{X_{3} }} = \overrightarrow {{X_{\delta } }} - \overrightarrow {{A_{3} }} \cdot \left( {\overrightarrow {{D_{\delta } }} } \right) $$
(17)
$$ \vec{X}\left( {t + 1} \right) = \frac{{\overrightarrow {{X_{1} }} + \overrightarrow {{X_{2} }} + \overrightarrow {{X_{3} }} }}{3}. $$
(18)

The pseudocode of the GWO algorithm is demonstrated in Fig. 5.

Fig. 5
figure 5

Pseudocode of the GWO algorithm

Full size image

3.3 The framework of the proposed model

The hybrid method proposed in this paper entails taking two steps: (1) the Lagrangian function that updates Lagrange multipliers and (2) the constrained global maximization of the ALR function, where GWO is applied to find an optimal solution. The flowchart of the proposed method is shown in Fig. 6.

Fig. 6
figure 6

Flowchart of the suggested model

Full size image

4 Numerical results

This paper developed, applied, and tested the proposed model in MATLAB R2019a environment. The tests above have been conducted on a PC with Intel Quad Core, 3.5 GHz CPU, and 32 GB of RAM. All formulations developed so far are verified by numerical experiments on a synthetic dataset with 4750 blocks. Table 2 implies the outperformance of the ALR–GWO method in terms of the optimality gap. Also, the parameters were fixed according to the model changes and convergence. In this paper, various metaheuristic algorithms have been used including grey wolf optimizer algorithm, bat algorithm, particle swarm optimization, and genetic algorithm. Table 3 illustrates the parameters applied to metaheuristic methods. Furthermore, the maximum number of iterations was utilized as the criterion for terminating iterations set at 1000 following the observation of the convergence behavior of the algorithm.

Table 2 Implementation of the proposed model for the synthetic dataset containing 4750 blocks
Full size table
Table 3 Parameters setting of metaheuristic methods
Full size table

The proposed integrated mine scheduling optimization framework has been applied to a real iron deposit. The iron deposit above contains 6854 blocks situated in Iran. Tables 4 and 5 provide the technical parameters and the number of model variables for the iron deposit, respectively.

Table 4 Technical parameters
Full size table
Table 5 Number of model variables
Full size table

The results of net present value (NPV) and average ore grade in uncertainty-based condition for the case study using LR-metaheuristic and ALR-metaheuristic approaches in the twelve production periods are illustrated in Figs. 7, 8, 9, and 10. Besides, the outcomes of NPV and average ore grade obtained by the conventional method without using the Lagrangian relaxation approach are presented.

Fig. 7
figure 7

Comparison of NPV obtained by LR-based presented methods considering grade uncertainty

Full size image
Fig. 8
figure 8

Comparison of NPV obtained by ALR-based presented methods considering grade uncertainty

Full size image
Fig. 9
figure 9

Comparison of average ore grade obtained by LR-based methods considering grade uncertainty

Full size image
Fig. 10
figure 10

Comparison of average ore grade obtained by ALR-based methods considering grade uncertainty

Full size image

The comparison of cumulative NPV and average ore grade in the total period in uncertainty-based condition for the case study obtained by all of the solution approaches is demonstrated in Figs. 11 and 12. As outcomes are shown, the ALR–GWO method generates more appropriate results than the other presented methods. The cumulative NPV and the average ore grade in the 12-year period considering grade uncertainty using the ALR–GWO method are 13.39% and 2.63% more than the conventional method, respectively.

Fig. 11
figure 11

Comparison of cumulative NPV in the total 12-year period obtained by hybrid methods

Full size image
Fig. 12
figure 12

Comparison of average ore grade in the total 12-year period obtained by hybrid methods

Full size image

5 Discussion

In open-pit mines, the LTPS problem is a MIP problem and is considered as the class of NP-hard problems that has to be solved in a reasonably small time due to the operational requirements. LTPS problem still cannot be considered a well-solved problem. Lagrangian relaxation method is widely and efficiently applied to solve optimization problems with complex constraints since it was brought forward in the 1960s. It often exploits the special decomposable structure of the initial problem to deal with large-scale complex problems in various fields, such as manufacturing scheduling, supply chain optimization, and production scheduling problems. The major purpose of this technique is to relax the structured coupling constraints, and surcharge them as a penalty to the objective function with the presentation of Lagrangian multipliers. A dual problem is thus organized with the multipliers as its variables and can be decomposed into easier solving subproblems. A two-level optimization framework is applied to solve the dual problem. The decomposed subproblems are solved individually at a low level with much less computational efforts and the Lagrange multipliers are coordinated and updated at a high level based on the level of constraints violation. In this study, the augmented Lagrangian relaxation method is used. The major advantage of the augmented Lagrangian relaxation over the Lagrangian relaxation is that the former may get a practicable solution in instances wherever initial and dual solutions give a duality gap.

To specify the multiplier values based on the past calculation outcomes, the authors use the subgradient method that is usually employed. According to the zigzag phenomenon and small steps, the subgradient method may join gradually on large problems. As noted in the literature review of manuscripts, the use of this method has increased in recent years by combining metaheuristic algorithms. They can be simply applied for the solution of hard optimization problems and they are responsible for great modeling flexibility. The results in different industries show the high performance of this model. In this research, different algorithms have been reviewed and tested for updating Lagrangian multipliers and chose the GWO algorithm based on the results of previous researches and the advantages of the various algorithms. According to the mentioned explanations, the combined method is a suitable option for the problem in the research and has the advantages such as ability to implement in large-scale long-term production scheduling problems in open-pit mines, reduce calculation time and cost, near-optimal final solution. Figure 13 provides an overview of the results of cumulative net present value over the entire 12-year period for the case study in terms of grade uncertainty. As can be seen in Fig. 13, ALR–GWO produces better result than other methods.

Fig. 13
figure 13

General view of the cumulative net present value results

Full size image

In fact, as stated, the greatest challenge in the LR method is to maximize the Lagrangian dual function efficiently, which is a concave multifaceted piecewise linear function. To determine multiplier values based on prior calculation results, the subgradient method has often been used. However, multipliers usually zigzag along the intersection of several facets of the Lagrangian dual function requiring a large number of repetitions to a maximum extent, albeit it may converge progressively. Based on the zigzag movement and small steps, the subgradient method may join step by step on big problems. Studying natural evolution influences metaheuristics global optimization algorithms. They can be utilized to solve hard optimization problems in charge of excellent modeling flexibility. In the context of the LR and ALR solutions to LTPS problem, metaheuristics approaches can be applied for dual variables. The main idea of the LR and ALR metaheuristics is that metaheuristics algorithms are integrated into the LR method to update the Lagrange multipliers. This method shows how LR is used in solving combinatorial optimization problems, including LTPS problem. According to the results of the averaging LR and ALR with GWO, BA, GA, and PSO algorithms, accelerating the convergence and greatly near-optimal solutions to LTPS problem can be finalized by the LR and ALR metaheuristics.

Table 6 shows the computation time and the optimality gap of each method. According to the evaluations, the CPU time is higher compared to other approaches that take advantage of the hybrid ALR–GWO technique proposed in this paper. Accordingly, these approaches drastically reduce computation time while keeping the optimality gap low. The latter implies the effectiveness of the proposed method. Besides, Fig. 14 displays that the iteration number according to the problem size of GWO is the minimum, and also, the iteration number of SG has high fluctuation when the problem scale gets bigger. Furthermore, the average cost-effectiveness ratio, best cost-effectiveness ratio, worst cost-effectiveness ratio, and deviation are presented in Table 7. As shown in Table 7, the results of GWO are superior to the other methods studied in this paper.

Table 6 An overview of the solution found by MATLAB for proposed models
Full size table
Fig. 14
figure 14

Comparing proposed models in terms of iteration number

Full size image
Table 7 Statistical results of the studied methods
Full size table

6 Conclusions

This paper proposed a hybrid technique to solve the LTPS problem in open-pit mines since it is a large-scale, complex problem. A novel method was also introduced to optimize Lagrange multipliers in the hybrid ALR–GWO method and to compare it with the SG method in terms of performance. The result of the case indicated the effectiveness of the hybrid ALR–GWO method to find a feasible solution for the LTPS problem. The hybrid strategy can produce a more effective solution to the extent of the near-optimal solution in comparison with the conventional method. Moreover, it was specified that the stable convergence property and prevention of early convergence are identified as the major advantages of the method suggested in this paper. In terms of cumulative NPV, average ore grade, and CPU time, results demonstrate that ALR–GWO generates best outcomes while satisfying constraints. The CPU time by the ALR–GWO hybrid method was 838.82% higher than the conventional method and also 8.73%, 24.09%, 35.53%, 68.60%, 3.53%, 15.76%, 33.19%, 39.10%, and 76.70%, more than the ALR-BA, ALR-PSO, ALR-GA, ALR-SG, LR-GWO, LR-BA, LR-PSO, LR-GA, and LR-SG procedures, respectively.

According to the results, further studies are required such as the application of the model presented in this paper for other iron ore mines as well as mines with different minerals, also, use of other existed methods for minimizing of large-scale and complex models instead of the Lagrangian relaxation method, furthermore, implementing of other metaheuristic methods for the proposed model and comparing their results with the methods presented in this research, besides, utilization of different variants of GWO such as binary grey wolf optimizer (BGWO) and multi-objective grey wolf optimizer (MOGWO) for implementation on LTPS problems, and finally, examining the effect of other uncertainties separately or simultaneously for the long-term production scheduling in future research.