1 Introduction

Graphene tubules are advanced remarkably as a result of numerous applications in science and engineering and it is due to its thermal, mechanical, physical, chemical and magnetic properties. Ebrahimi et al. [1] employed the nonlocal elasticity theory and analyzed the vibration characteristics of rotating non-homogeneous nanobeam using power-law model, Hamilton’s principle and Euler Bernoulli beam theory. Later Ebrahimi and Haghi [2] investigated the dispersion characteristics of rotating nanotube under the thermal environment within the framework of the Galerkin approach. Chan and Zhao [3] developed an inexpensive model to examine the dispersal features of spinning single walled carbon nanotube (SWCNT). Narendar [4] modelled a rotating nanotube utilizing the Euler Bernoulli beam theory predicated on continuum mechanics. Later the same author [5] developed the nonlocal flap wise wave propagation of rotating nanotube. Narendar et al. [6] deliberate the dispersion features of magnetic response of SWCNTs. Wang et al. [7] examined the outcome of thermal and magnetic response on tera hertz wave conception in fluid conveying SWCNT.

Kiani [8] examined the magnetic response of nonlocal flexural wave conception of SWCNTs using Timoshenko, nonlocal Rayleigh and higher-order beams. Wang et al. [9] proposed the magnetic response of propagation of waves fixed in stretchy medium. Guven [10] dispensed the magnetic response of the flexural wave propagation of SWCNT. Ponnusamy and Amuthalakshmi [11] studied the response of thermo magnetic force on fluctuation in double walled carbon nanotubes utilizing nonlocal Timoshenko beam theory. Further the same authors [12] studied the vibration features of electro-magneto-thermo-elastic fiber with the assistance of three-dimensional theory of elasticity. Li et al. [13] formulated the vibration equations of viscoelastic SWCNTs under the surface and magnetic field.

Arda and Aydogdu [14] investigated the torsional vibration behaviour of nanotubules with multiwalled under van der Waals interaction and non-local effect. Further the same author [15] presented the torque and magnetic force on the nonlocal propagation of nanotubes utilizing Hamilton’s principle and Maxwell’s relation. She et al. [16] proposed the propagation of waves of porous nanotubes formulated from nonlocal strain theory. Dehghan et al. [17] analyzed the conception of waves of fluid carrying nanotubules exposed to thermo magnetic force.

Mohammadi et al. [18] studied the influence of temperature on the wave propagation of the mono-layer graphene sheet embedded in an elastic medium. Based upon Navier and Levy’s solution an analytical dispersion equation of graphene sheets is obtained. Farajpour and Rastoo [19] developed a modified beam model and investigated the effect of carbon nanotubes on the buckling of microtubule bundles in the living cells. The authors applied the Pasternak model, surface elasticity theory and nonlocal gradient theory to examine the normal and shearing effect, surface effect and small scale effect of carbon nanotubes. Later the author with Farokhi [20] developed a scale-dependent coupled nonlinear continuum-based model for the mechanical behaviour of imperfect nanoscale tubes.

Li et al. [21] employed that there are different kinds of nonlocal elasticity approaches including softening and hardening models. In particular, the authors studied the longitudinal dynamic behaviour of common one-dimensional nanostructures using the hardening nonlocal approach. Yao et al. [22] investigated the wave propagation characteristics of functionally graded Timoshenko beams using the differential quadrature method. Further, the authors revealed that there are both nonlocal strengthening and weakening models in wave propagation and they are related to different types of surface effects. Li [23] investigated an analytical approach with the consideration of nonlocal effect for the torsion of cylindrical nanostructures and the existence of higher-order stress and geometric boundaries. Liu et al. [24] developed a higher-order mechanical model of axially moving nanoscale beams with time-dependent on the framework of nonlocal stress gradient theory.

In this paper, the propagation of waves of thermo magnetic effect of nonlocal rotating graphene tubules is studied using non-local continuum mechanics. The vibration equations of motion are derived by applying the nonlocal effect, the constant axial force exerted by thermal and centrifugal effect and magnetic force exerted by Lorentz magnetic effect. The thermo magnetic response of the rotating graphene tubule is employed using Euler–Bernoulli beam theory. The dispersion relation is derived in terms of wave number for thermo magnetic response of rotating graphene tubule. The calculated wave numbers are represented in terms of scattered curves.

2 Formulation of the problem

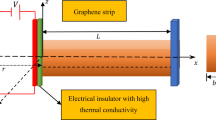
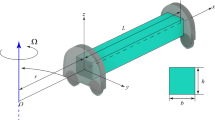
Consider a rotating graphene tubule subjected to thermo magnetic field as revealed in Fig. 1. and it can be constituted to a rigid beam with its translation perpendicular to the rotation in space. The strain and displacement relation for beams is given by

$$\varepsilon_{xx} = \frac{\partial u}{{\partial x}} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(1)

where x is the axial coordinated and u denotes the axial deflection and w denotes the flexural deflection of rotating beam in z direction. The strain \(\varepsilon_{xx}\) denotes the deflection strain or curvature of the beam.

Fig. 1
figure 1

A rotating graphene tubule subjected to thermo magnetic force

Full size image

Applying engineer’s beam theory to a rotating graphene tubule exposed to magnetic and thermal force, the governing mathematical equation is constituted as [25]

$$\frac{{\partial^{2} M}}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left[ {N_{t} \frac{\partial w}{{\partial x}} + T\left( x \right)\frac{\partial w}{{\partial x}}} \right] + q = \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(2)

where M, Nt, T(x) and q denotes the bending moment, axial force due to thermal effect, axial force due to centrifugal stiffening and magnetic force per unit length respectively regarded as [13, 25, 26]

$$M = \int\limits_{A} {z\sigma_{xx} dA}$$
(3)
$$N_{t} = - \alpha EAT$$
(4)
$$T\left( x \right) = \int\limits_{x}^{L} {\rho A\Omega^{2} x} dx$$
(5)
$$q = \int\limits_{A} {f_{z} dz} = \eta AH_{x}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(6)

in which \(\sigma_{xx} ,\)\(A,\)\(\alpha ,\)\(E,L,\)\(T,\)\(\rho ,\)\(\Omega ,\)\(\eta\) and \(H_{x}\) indicates respectively the normal stress, cross-section area of tubule, thermal extension, modulus of elasticity, length of graphene tubule, temperature, mass density, rotation speed, magnetic permeability and longitudinal magnetic field.

Assume the rotating graphene tubule is of the homogeneous isotropic medium. The stress and strain relation based on nonlocal elasticity theory is given by

$$\sigma_{xx} - \left( {e_{0} a} \right)\frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx}$$
(7)

where \(e_{0} a\) denotes the nonlocal parameter.

Substituting Eq. (7) in Eq. (3), the nonlocal bending relation in terms of moment of inertia and curvature is acquired in the form

$$M - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = EI\kappa$$
(8)

where \(I\) and \(\kappa\) denotes the rotational inertia and measure of inflection obtained as \(I = \int\nolimits_{A} {z^{2} dA}\) and \(k = - \tfrac{{\partial^{2} w}}{{\partial x^{2} }}.\) Further substituting Eq. (8) in the governing Eq. (2), the nonlocal vibration of a rotating graphene tubule with magnetic and thermal effect in mathematical form can be obtained as follows

$$EI\frac{{\partial^{4} w}}{{\partial x^{4} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left\{ {\rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{\partial }{\partial x}\left[ {N_{t} \frac{\partial w}{{\partial x}} + T\left( x \right)\frac{\partial w}{{\partial x}}} \right] - q} \right\} - \frac{\partial }{\partial x}\left( {N_{t} + T\left( x \right)} \right)\frac{\partial w}{{\partial x}} - q + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} = 0$$
(9)

With the assumption of steady revolving cantilever beam, the function \(T\left( x \right)\) mentioned in Eq. (5) according to \(x = 0\) becomes the minimum force and is specified as [25]

$$T_{\max } = \int\limits_{0}^{L} {\rho A\Omega^{2} x} dx = \frac{{\rho A\Omega^{2} L^{2} }}{2}$$
(10)

Substituting Eqs. (6) and (10) in Eq. (9), the partial differential equation with constant coefficients can be regarded as

$$\left\{ {EI + \left( {e_{0} a} \right)^{2} \left[ {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right]} \right\}\frac{{\partial^{4} w}}{{\partial x^{4} }} - \left( {e_{0} a} \right)^{2} \rho A\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - \left( {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} = 0$$
(11)

Equation (11) is known to be the flexural vibration equation of nonlocal rotating graphene tubule under the response of thermo-magnetic effect.

3 Solution of the problem

In an effort to explore the dispersal characteristics of thermo-magnetic response of nonlocal rotating graphene tubule a harmonic solution for Eq. (11) is assumed in terms of flexural deflection and is provided in the form

$$w\left( {x,t} \right) = \sum\limits_{n = 1}^{N} {\widetilde{w}} e^{{i\omega_{n} t}}$$
(12)

where \(\widetilde{w},\)\(\omega_{n}\) and \(N\) denotes the amplitude, angular frequency and number of amples of flexural vibration of rotating graphene tubule. The amplitude \(\widetilde{w}\) is a function of \(x\) and \(\omega_{n} .\) Further it is noted that the natural frequency of grahene tube is given by \(\omega_{str} = \frac{1}{{L^{2} }}\sqrt {\frac{EI}{{\rho A}}}\).

Substituting the solution Eq. (12) in Eq. (11), the following equation is obtained

$$\sum\limits_{n = 1}^{N} {\left\{ {\left[ {EI + \left( {e_{0} a} \right)^{2} \left( {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right)} \right]\frac{{\partial^{4} \widetilde{w}}}{{\partial x^{4} }} + \left( {e_{0} a} \right)^{2} \rho A\omega_{n}^{2} \frac{{\partial^{2} \widetilde{w}}}{{\partial x^{2} }} - \left( {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right)\frac{{\partial^{2} \widetilde{w}}}{{\partial x^{2} }}} \right.} \left. { - \rho A\omega_{n}^{2} \widetilde{w}} \right\}e^{{i\omega_{n} t}} = 0$$
(13)

Equation (13) is satisfied for every \(n\) and hence it is rewritten in the form

$$\left[ {EI + \left( {e_{0} a} \right)^{2} \left( {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right)} \right]\frac{{d^{4} \widetilde{w}}}{{dx^{4} }} + \left( {e_{0} a} \right)^{2} \rho A\omega^{2} \frac{{d^{2} \widetilde{w}}}{{dx^{2} }} - \left( {N_{t} + T_{\max } + \eta AH_{x}^{2} } \right)\frac{{d^{2} \widetilde{w}}}{{dx^{2} }} - \rho A\omega^{2} \widetilde{w} = 0$$
(14)

Introducing the non-dimensional quantities such as \(\overline{x} = \frac{x}{L},\)\(\overline{w} = \frac{{\widetilde{w}}}{L},\)\(\frac{{d\widetilde{w}}}{dx} = \frac{{d\overline{w} }}{{d\overline{x} }},\)\(\frac{{d^{2} \widetilde{w}}}{{dx^{2} }} = \frac{1}{L}\frac{{d^{2} \overline{w} }}{{d\overline{x}^{2} }},\)\(\frac{{d^{3} \widetilde{w}}}{{dx^{3} }} = \frac{1}{{L^{2} }}\frac{{d^{3} \overline{w} }}{{d\overline{x}^{3} }},\)\(\frac{{d^{4} \widetilde{w}}}{{dx^{4} }} = \frac{1}{{L^{3} }}\frac{{d^{4} \overline{w} }}{{d\overline{x}^{4} }},\)\(\varepsilon = \frac{{e_{0} a}}{L},\)\(\varsigma = \frac{\Omega }{{\omega_{str} }},\)\(\xi = \frac{\omega }{{\omega_{str} }},\)\(\overline{N}_{t} = \frac{{N_{t} }}{{L^{2} \rho A\omega_{str}^{2} }}\) and \(\overline{\eta } = \frac{{\eta H_{x}^{2} }}{{L^{2} \rho \omega_{str}^{2} }}\) in Eq. (14), the governing differential equation in terms of non-dimensional form is obtained as follows

$$\left( {1 + \overline{N}_{t} \varepsilon^{2} + \frac{1}{2}\varepsilon^{2} \varsigma^{2} + \overline{\eta } \varepsilon^{2} } \right)\frac{{d^{4} \overline{w} }}{{d\overline{x}^{4} }} + \left( {\varepsilon^{2} \xi^{2} - \overline{N}_{t} - \frac{1}{2}\varsigma^{2} - \overline{\eta } } \right)\frac{{d^{2} \overline{w} }}{{d\overline{x}^{2} }} - \xi^{2} \overline{w} = 0$$
(15)

4 Dispersion relation

The dimensionless governing equation of a graphene tubule with nonlocal, thermal and magnetic field obtained in Eq. (15) is an ordinary differential equation with constant coefficient. Therefore the variable separable solution to the Eq. (15) is specified in the form

$$\overline{w} = \overline{A} e^{ - ikx}$$
(16)

where \(\overline{A}\) and \(k\) designates the amplitude and non-dimensional repetency or wave number of graphene tubule. On replacing Eq. (16) in the dimensionless governing Eq. (15), the dispersal equation concerning repetency and frequency is obtained as follows

$$\left( {1 + \overline{N}_{t} \varepsilon^{2} + \overline{\eta } \varepsilon^{2} + \frac{1}{2}\varepsilon^{2} \varsigma^{2} } \right)k^{4} + \left( {\overline{N}_{t} + \overline{\eta } + \frac{1}{2}\varsigma^{2} - \varepsilon^{2} \xi^{2} } \right)k^{2} - \xi^{2} = 0$$
(17)

On solving Eq. (17), the wave number of rotating graphene tubule with nonlocal effect exposed to thermo magnetic response is procured as follows

$$k = \pm \sqrt {\frac{{ - \left( {\overline{N}_{t} + \overline{\eta } + \frac{1}{2}\varsigma^{2} - \varepsilon^{2} \xi^{2} } \right) \pm \sqrt {\left( {\overline{N}_{t} + \overline{\eta } + \frac{1}{2}\varsigma^{2} - \varepsilon^{2} \xi^{2} } \right)^{2} + 4\xi^{2} \left( {1 + \varepsilon^{2} \left( {\overline{N}_{t} + \overline{\eta } + \frac{1}{2}\varsigma^{2} } \right)} \right)} }}{{2\left( {1 + \varepsilon^{2} \left( {\overline{N}_{t} + \overline{\eta } + \frac{1}{2}\varsigma^{2} } \right)} \right)}}}$$
(18)

The numerical value of non-dimensional wave numbers can be computed using Eq. (18) and it is a function of non-dimensional thermal force, non-dimensional magnetic force, non-dimensional rotating speed and non-dimensional frequency.

5 Numerical results and discussion

To analyze numerical results, a graphene tubule is considered with its numerical information taken from [25] as diameter of graphene tubule \(d = 0.675\,{\text{nm}},\) modulus of elasticity \(E = 5.5\,{\text{TPa}},\) length of graphene tubule \(L = 10d,\) and density \(\rho = 2300\,{\text{kg/m}}^{{3}} .\) From Li et al. [13], magnetic strength and its permeability is considered as Ĥ = \(H_{x} = 10^{7} \,{\text{A/m}}\) and \(\eta = 4\pi \times 10^{ - 7} \,{\text{H/m}}.\) The value of temperature and thermal expansion [26] is \(T = 25\,{\text{K}}\) and \(\alpha_{x} = - 1.6 \times 10^{ - 6} K^{ - 1} .\,\)

Dispersion curves are drawn for rotating graphene tubule with magnetic and thermal effect for \(\tau = 0\) at different values of non-dimensional rotational speed and are shown in Fig. 2. Figure 2 exhibit that larger the values of rotational speed its non-dimensional wave number gets decreased. Further, it remarked that if the non-dimensional frequency is strengthened its corresponding wave number becomes stronger. The waves become non-dispersive as the value of non-dimensional rotation speed increases. The change in the behaviour of wave number is because of its rotational speed caused by the centrifugal force.

Fig. 2
figure 2

Dispersion of non-dimensional wave number \(k\) of a rotating graphene tubule exposed to thermo magnetic force for \(\varepsilon = 0\) with different non-dimensional rotating speed \(\varsigma\)

Full size image

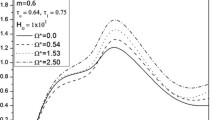
Scattered curves are sketched for a rotating nonlocal graphene tubule with thermal and magnetic field for \(\varsigma = 0\) and \(\varsigma = 10\) at different nonlocal parameter \(\varepsilon\) respectively and are revealed as Figs. 3 and 4. Figures 3 and 4 remarked that as the non-local parameter \(\varepsilon\) gets larger the non-dimensional wave number \(k\) also gets larger. In addition, noticed that wave number has lesser value in the absence of nonlocal parameter \(\varepsilon\). It is seen that the dispersion curves are linear for higher values of dimensionless frequency \(\xi\). The value of dimensionless wave number gets decreased for \(\varsigma = 10\) compared to \(\varsigma = 0\). Further only slight variation in the value of wave number is seen for tubules with rotation speed in comparison with non-rotational speed. Further from Figs. 3 and 4, it is observed that the curves have a linear dependence nature at the lower values of dimensionless frequency \(\xi\) especially below 5. But at the higher values of frequency, the variation of non-dimensional wave number \(k\) is large and this is due to the dominance of the centrifugal force at higher values of frequency.

Fig. 3
figure 3

Scattered curves of a nonlocal rotating graphene tubule exposed to thermo magnetic force for \(\varsigma = 0\) with distinct nonlocal parameter \(\varepsilon\)

Full size image
Fig. 4
figure 4

Scattered curves of nonlocal rotating graphene tubule exposed to thermo magnetic force for \(\varsigma = 10\) with distinct nonlocal parameter \(\varepsilon\)

Full size image

Scattered curves are dawn for a thermo magnetic response of nonlocal rotating graphene tubule at different temperatures and are shown in Fig. 5. Figure 5 perceived that increasing the value of frequency at some nonlocal parameter increases the value of wave number. In addition, integrated value of wave number \(k\) decreases as the temperature \(T\) caused by axial force due to thermal effects increases. It is also seen that the waves are linear with respect to temperature change. Scattered curves are plotted for thermo-magnetic response of nonlocal rotating graphene tubule at different magnetic field strength and are revealed in the form of Fig. 6. Figure 6 exhibit that incrementing the magnetic field strength Ĥ of graphene tubule decreases the integrated value of non-dimensional wave number \(k.\)

Fig. 5
figure 5

Scattered curves of a rotating graphene tubule exposed to thermo magnetic effect for \(\varsigma = 10,\)\(H_{x} = 10^{7} A/m\) and \(\varepsilon = 0.1\) with different temperature \(T\)

Full size image
Fig. 6
figure 6

Scattered curves of a rotating graphene tubule exposed to thermo magnetic effect for \(\varsigma = 10,\)\(T = 25K\) and \(\varepsilon = 0.1\) with different magnetic field strength Ĥ

Full size image

Scattered curves of a non-rotating graphene tubule without thermal and magnetic field at different non-local parameter are drawn and are shown in Fig. 7. From Fig. 7, it is observed that the non-dimensional wave number \(k\) increases as dimensionless frequency decreases. Further it is observed that the non-dimensional wave number increases as the non local parameter increases. The dispersion curves of a non-rotating graphene tubule without thermal and magnetic field matches with the Fig. 4a of Narendar and Gopalakrishnan [25] and it shows the accuracy of the present result.

Fig. 7
figure 7

Scattered curves of a non-rotating graphene tubule without thermal and magnetic effect at different non-local parameter

Full size image

6 Conclusion

The thermo magnetic response of graphene tubule with nonlocal effect is elaborated with the aid of classical beam theory. The dispersal properties of graphene tubules under thermal, nonlocal and magnetic field are analyzed using the dispersion curves. Numerically the non-dimensional wave numbers of graphene tubule are computed respectively for different non-rotational speed, nonlocal parameter, temperature and magnetic field strength. It is shown that the presence of rotation speed, temperature and magnetic field decreases the value of wave number. Further the existence of frequency and nonlocal parameter strengthens the integrated value of wave number. The dispersion curves of non-rotating graphene tubule without a thermal and magnetic field are compared with the existing literature and this shows the exactness of the present result.