1 Introduction

Settlement of structures founded on deformable soil strata is a subject of particular significance to the whole geotechnical community, as it may lead to critical disastrous serviceability problems. Having encountered the excessive foundation settlement as the substantial criteria of stability, the structure may possibly fail to perform efficiently. This could result in an irrevocable operational demolition. The aforementioned serviceability issue may be manifested through both the absolute settlement of a single footing as well as the differential settlement of the adjacent foundations, although the latter is the predominant reason of the most destructive structural deformations. Adopting the theory of elasticity concepts, immediate settlement of shallow foundations is typically assessed for a homogeneous and isotropic soil medium using constant values for the soil elastic modulus and Poisson’s ratio, which are denoted as E and v, respectively. However, the assumptions of homogeneity and isotropy for the soil properties have triggered the respective correlations for the settlement calculations to be admittedly futile and inefficient for most practical geotechnical problems. Indeed, the conventional equations for settlement assessment are always accompanied with an appropriate, and inevitably high, factor of safety to compensate the inherent uncertainties and to assure the suitable performance of the foundation. These analyses, however, might lead to highly unconservative geotechnical design. Therefore, spatial variability and the uncertainties involved in the evaluation of soil properties in the field are an inseparable part of any geotechnical analysis which must never be disregarded [1,2,3,4,5]. Accordingly, the probabilistic analysis of geo-structures seems to be essential and is required to be performed prior to any constructions.

Throughout the literature, innumerable attempts have been made to incorporate uncertainty and probability concepts into a variety of geotechnical problems, with the seminal contributions of the studies carried out by Fenton and Griffiths [2,3,4, 6, 7]. Among the various geotechnical topics studied through the stochastic approaches, the bearing capacity and settlement of shallow foundations, slope stability and the liquefaction hazards are of tremendous importance [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. In these studies, adopting variable stochastic parameters of interest including mean and variance, a variety of well-established numerical models were combined with the random field theory concepts and Monte Carlo simulations (MCSs) in order to assess the failure probability and design reliability of geo-structures.

In order to look more specific, there exist several research studies in the literature on the settlement evaluation of geo-structures using the random field theory [2, 6, 8, 25,26,27,28,29,30,31,32]. In most of these studies, elastic modulus, which is supposed to be a measure of soil stiffness and deformability, was considered as the primary random variable in the probabilistic assessment of foundation settlement. Due to its nonnegative nature, soil elastic modulus is widely represented by a log-normal distribution function [2, 29, 30]. In a comprehensive study conducted by Jimenez and Sitar [31], an extensive sensitivity analysis was carried out to explore the effects of adoption of the different types of statistical distribution for elastic modulus on the foundation settlement. In another pioneer parametric study performed by Fenton and Griffiths [2], numerous Monte Carlo simulations were incorporated into the finite element analysis to generate several random realizations in order to examine the influence of foundation width and standard deviation and scale of fluctuation of elastic modulus on the total and differential settlement of shallow footings. Based on the results of their study, the associated probabilities with both types of settlements were observed to be conservatively evaluated through the use of a normal distribution function with the respective parameters well approximated by the statistics of the local averages of the log-elastic modulus field directly beneath each footing. In another separate study performed by Fenton and Griffiths [6], the foundation settlement and failure probability have been assessed using a three-dimensional spatially random soil modeling.

In all the aforementioned probabilistic studies on the immediate settlement of shallow foundations, the soil behavior was supposed to be isotropic, bearing quite similar properties in variable directions inside the soil medium. However, as most natural soils are the consequences of long-lasting sedimentary deposition upon considerable overburden pressure, their formation leads to the generation of several layered horizontal planes. This, in turn, poses their elastic properties in variable directions to be different. Indeed, all types of soils exhibit anisotropic behavior depending on their geological characteristics, deposition process and applied stress history.

To the best of authors’ knowledge, there exists no study throughout the literature on the probabilistic analysis of foundation settlement on heterogeneous random soil with the particular attention to the soil mechanical anisotropy. To fill this gap, in the course of this study, following the decent work performed by Fenton and Griffiths [2], soil mechanical anisotropy is incorporated into the probabilistic settlement analysis of heterogeneous deposits. To this end, adopting the modulus of elasticity as the governing random parameter with a log-normal probability distribution, comprehensive number of Monte Carlo simulations is combined with the finite element modeling of settlement predictions. Using the results of the probabilistic simulations of the footings founded on the heterogeneous and anisotropic soil stratum, the respective stochastic parameters of the total and differential settlement are elaborated. Finally, the results of the immediate settlement evaluation using the random finite element approach are compared to those of the conventional methods.

2 Statistical concepts

Due to the large amount of uncertainties involved in any geotechnical problems, quantitative probabilistic analysis of soil spatial variability in such analyses using random field theory would lead to more realistic, thus more conservative outcomes. Inherent soil spatial variability refers to the general variation of soil properties among the points throughout the soil medium. Accounting for a typical soil property, denoted as “x” herein, as the random variable across the problem domain, its geo-statistical parameters could be described through different stochastic measures, including the mean (\(\mu_{x}\)), variance (\(\sigma_{x}^{2}\)), standard deviation (\({\text{SD}}_{x} \;{\text{or}}\; \sigma_{x}\)) and coefficient of variation (\({\text{COV}}_{x}\)). The aforementioned statistical parameters are typical one-point measures, incapable of expressing the soil properties spatial variability within the soil medium. In this regard, an independent parameter, known as scale of fluctuation, is usually implemented to fully characterize the spatial variabilities of parameters in the problem domain. The scale of fluctuation, typically denoted by θ, is defined as the distance beyond which the random variables, which are soil properties in this study, are no longer correlated with each other. Indeed, the scale of fluctuation is a measure of dependency or correlation among the different values of a specific soil property at various locations throughout the problem domain. While rough random fields possess small values of scale of fluctuation, a quite smooth random field can be represented by the greater values of θ. As the scale of fluctuation increases and moves toward the infinity, a perfectly correlated random field is generated with the spatially random (through realizations) and constant (in each realization) variables.

In this study, it is assumed that the soil elastic modulus follows a log-normal distribution, so that \({ \ln }\left( E \right)\) is a Gaussian (normal) random field. This type of variation has been adopted due to the nonnegative nature of elastic modulus, which assures it to be a decent nominee for such a distribution. Realizations of the log-elastic modulus field in this study are generated using the well-established two-dimensional local average subdivision (LAS) technique, originally proposed by Fenton and Vanmarcke [33] and Fenton [34] and then implemented by Fenton and Griffiths [2] for the settlement analysis of the foundation on an isotropic, heterogeneous soil layer. Adopting various zones (elements) in the problem domain, the general stochastic log-normal distribution for the soil elastic modulus assigned to the i’th element could be presented as follows:

$$E\left( {x_{i} } \right) = { \exp }\left( {\mu_{lnE} + \sigma_{lnE} . G\left( {x_{i} } \right)} \right)$$
(1)

where \(\mu_{lnE}\) and \(\sigma_{lnE}^{ }\) are the mean and standard deviation of the logarithm of \(E\), respectively. \(G\left( {x_{i} } \right)\) is a local average, over the i’th element centered at \(x_{i}\) of a zero mean, unit variance Gaussian random field.

The mean (\(\mu_{lnE}\)) and variance (\(\sigma_{lnE}^{2}\)) of the log-elastic modulus are obtained adopting the following typical log-normal distribution transformations:

$$\mu_{lnE} = \ln \left( {\mu_{E} } \right) - \frac{1}{2}\sigma_{lnE}^{2}$$
(2)
$$\sigma_{lnE}^{2} = ln\left( {1 + {\raise0.7ex\hbox{${\sigma_{E}^{2} }$} \!\mathord{\left/ {\vphantom {{\sigma_{E}^{2} } {\mu_{E}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{E}^{2} }$}}} \right) = ln\left( {1 + {\text{COV}}_{\text{E}}^{2} } \right)$$
(3)

3 Definition of anisotropy

Two major types of soil anisotropy could be distinguished, expressed as mechanical or stiffness anisotropy and heterogeneous anisotropy. Mechanical anisotropy is defined as the non-uniqueness of the physical properties of an anisotropic soil layer along different directions. On the other hand, heterogeneous anisotropy could be described as the difference in the auto-correlation distance of the soil properties in various directions. In this study, the soil is considered to be heterogeneously isotropic, but mechanically anisotropic. Indeed, the elastic modulus, which is the primary random variable of this study, is set to be different in the vertical and horizontal directions, while its scale of fluctuation (θ) is the same allover the soil layer. The horizontal and vertical axial elastic moduli are denoted by \(E_{\text{h}}\) and \(E_{\text{v}}\), respectively, and they were both taken as two fully correlated random fields. Furthermore, their proportion, shown by n, is defined as the axial stiffness anisotropy ratio, i.e., \(n = {\raise0.7ex\hbox{${E_{\text{h}} }$} \!\mathord{\left/ {\vphantom {{E_{\text{h}} } {E_{\text{v}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{v}} }$}}\). In addition, another measure of anisotropy, named as the shear stiffness anisotropy ratio (m), is defined as the ratio of the shear modulus in the vertical plane (\(G_{\text{vh}}\)) and the vertical modulus of elasticity, i.e., \(m = {\raise0.7ex\hbox{${G_{\text{vh}} }$} \!\mathord{\left/ {\vphantom {{G_{\text{vh}} } {E_{\text{v}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{\text{v}} }$}}\). The range of variation for the axial and shear stiffness anisotropy ratios used in the numerical simulations is presented in the following sections. It is worth noting that the elastic parameters in the cross-anisotropic case are not limited to the above-mentioned three elasticity parameters in drained condition. Generally, five elasticity parameters, namely three deformation moduli and two Poisson’s ratios, are considered. However, two Poisson’s ratios, one in the horizontal plane (νhh) and another one in the vertical plane (νvh or νhv), deemed less important in immediate settlement analyses though, are remained constant or dependent on others throughout the analyses due to the undrained condition assumption taken in the current study. In the undrained condition, the five independent cross-anisotropic parameters are reduced to 3 since νvh = 0.5 and νhh = 1 − νhv where \(\nu_{\text{hv}} = \frac{1}{2}n\) and no volume change is exhibited.

4 Numerical simulation

A typical stochastic model could be recognized as an indicative simulation of the continuous spatial variations in the soil properties within the soil medium. In other words, the soil mechanical properties at any arbitrary locations inside the soil strata are simulated through appropriate and well-defined random variables. Soil elastic modulus is set to be the primary random variable in this study for settlement evaluation which is supposed to follow a log-normal distribution across the soil profile due to its nonnegative nature. In order to generate the random field of the elastic modulus for the estimation of the immediate settlement in natural heterogeneous deposits, two-dimensional finite element modeling (FEM) in the form of visual Fortran programming is employed. In order to simulate the whole possible scenarios in the evaluation of settlement density function, several Monte Carlo simulations (MCS) have been implemented. Based on the preliminary concepts of this approach, with several generated random realizations, variable elastic moduli are assigned to the different elements in the model. Afterward, using the results of analysis for more than 3000 possible states for each bunch of input parameters, multiple realizations of the total and differential settlements of shallow foundations are obtained from which several stochastic distribution parameters can be estimated.

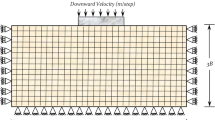
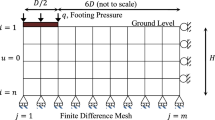
The numerical simulations in this study are performed for two different situations. In the first stage, a single spread footing is founded on a heterogeneous soil layer to examine the variation of immediate total settlement due to the variation of different stochastic parameters. In the second case, two adjacent shallow footings are founded on similar heterogeneous soil strata to explore the variation of differential settlement, which could be the primary source of most structural failures. The respective effective depth and problem domain as well as the restrictive bottom and lateral constraints used for these two cases are represented in Figs. 1 and 2. In the finite element modeling, plane strain conditions along with the four-node elements are adopted in all simulations and all analyses are performed using either precise or reduced integration. According to the geometries of the problem domain, presented in Figs. 1 and 2, the soil beneath the foundation in the influence area of the applied stress is divided into 60 horizontal and 20 vertical elements for the single footing case and 80 horizontal and 40 vertical elements for the case of two adjacent footings. The bottom boundary of the models is restricted against any horizontal and vertical movements to simulate the soil condition resting on hard bedrock. The lateral boundaries are also confined to any horizontal movements, but free to deform vertically to simulate soil settlement. Furthermore, the shallow footings are assumed to be rigid with quite rough interaction with the soil beneath.

Fig. 1
figure 1

Simulation of a single spread footing model for total settlement evaluation

Full size image
Fig. 2
figure 2

Simulation of a pair of spread footings model for differential settlement evaluation

Full size image

The effective parameters of interest in this study are the width of foundation (Wf), soil elastic modulus (E), coefficient of variation of the elastic modulus (COVE), auto-correlation distance or scale of fluctuation (θ) and axial and shear stiffness anisotropy ratios (n and m, respectively). The ranges of variation for the aforementioned parameters in this study are summarized in Table 1.

Table 1 Range of variations for the variable parameters used in the numerical simulations
Full size table

5 Simulation results and discussion

5.1 A single spread footing

The initial series of simulations in this study are performed to examine the variation of immediate settlement of a single spread footing founded on an anisotropic and heterogeneous soil layer due to the variation of the soil elastic modulus. Adopting a log-normal distribution for the elastic modulus of the soil, the respective stochastic parameters for the log-normal distribution of foundation settlement have been characterized by Fenton and Griffiths [2] as a function of several input parameters, including foundation width (\(W_{\text{f}}\)), standard deviation of elastic modulus (\(\sigma_{\text{E}}\)) and standard deviation of log-elastic modulus (\(\sigma_{lnE}\)), as follows:

$$f_{\delta } \left( x \right) = \frac{1}{{\sqrt {2\pi } \sigma_{ln\delta } x}}{ \exp }\left[ { - \frac{1}{2}\left( {\frac{{lnx - \mu_{ln\delta } }}{{\sigma_{ln\delta } }}} \right)^{2} } \right] ,\quad 0 \le x < \infty$$
(4)

where \(\mu_{ln\delta }\) and \(\sigma_{ln\delta }\) are the mean and standard deviation of log-settlement, respectively. In an isotropic condition, Fenton and Griffiths [2] proposed the following general linear correlation for the evaluation of the mean log-settlement:

$$\mu_{ln\delta } = ln\left( {\delta_{ \det } } \right) + \frac{1}{2}\sigma_{lnE}^{2}$$
(5)

where \(\sigma_{lnE}^{2}\) is the variance of log-elastic modulus and \(\delta_{ \det }\) is the deterministic settlement of foundation resting on an isotropic soil with a constant elastic modulus of \(E = \mu_{\text{E}}\). In a general sense, Eq. (5) could be presented in the following form:

$$\mu_{ln\delta } = ln\left( {\delta_{ \det } } \right) + \alpha \sigma_{lnE}^{2}$$
(6)

where \(\alpha\) is a model parameter.

The estimated values for \(\mu_{ln\delta }\) and \(\sigma_{lnE}^{ }\) are presented with \(m_{ln\delta }\) and \(s_{ln\delta }\), respectively. Figure 3 shows the variation of \(m_{ln\delta }\) with \(\sigma_{lnE}^{2}\), for the elastic modulus equal to 50 MPa, foundation width equal to 1 m and an isotropic soil condition with n = 1 and m = 1/3. Based on the results shown in this figure, the mean log-settlement increases with the increase in the variance of the log-elastic modulus. In addition, according to the simulation results presented in Fig. 4, the standard deviation of log-settlement (\(s_{ln\delta }\)) follows an ascending trend with the increase in the scale of fluctuation for log-elastic modulus and coefficient of variation of the elastic modulus. However, with an increase in the width of foundation, \(s_{ln\delta }\) decreases, which is more pronounced at higher variation of the elastic modulus. Furthermore, the typical variation of mean foundation settlement against the coefficient of variation of the elastic modulus in the isotropic soil state is shown in Fig. 5. As can be observed in this figure, the mean foundation settlement values are quite sensitive to the coefficient of variation of the elastic modulus, following an explicit ascending trend of up to 25% with COVE. Having a closer look into the numerous simulations results, it can be generally inferred that while the mean foundation settlement follows a linear variation with the coefficient of variation of the elastic modulus at low scales of fluctuation, the corresponding trend exhibits nonlinearity at higher values of θ.

Fig. 3
figure 3

Variation of mean logarithm of foundation settlement against the variance of log-elastic modulus in the case of isotropic condition with n = 1, m = 1/3, E = 50 MPa and Wf = 1 m for various scales of fluctuation

Full size image
Fig. 4
figure 4

Variation of standard deviation of logarithm of foundation settlement against the scale of fluctuation of log-elastic modulus in the case of isotropic condition with n = 1, m = 1/3 and E = 50 MPa for various widths of foundation

Full size image
Fig. 5
figure 5

Variation of mean foundation settlement against the coefficient of variation of the elastic modulus in the case of an isotropic condition with n = 1, m = 1/3, E = 50 MPa and Wf = 1 m for various scales of fluctuation

Full size image

Adopting the aforementioned definitions for the axial and shear stiffness anisotropy ratios in the previous sections as well as using the corresponding ranges of variation for the parameters of interest as presented in Table 1, several numerical simulations for the settlement assessment of a single footing on an anisotropic soil layer have been performed. A typical result of such analyses is presented in Fig. 6, showing the variation of mean log-settlement against the variance of log-elastic modulus for Wf = 1 m, E = 12.5 MPa, n = 3.5, m = 1/6 and various scales of fluctuation. As can be observed in this figure, although the increase in the scale of fluctuation has caused a significant rise in the estimated settlements, the trend of settlement variation with the variance of log-elastic modulus remains yet linear.

Fig. 6
figure 6

Variation of mean logarithm of foundation settlement against the variance of the log-elastic modulus in the case of an anisotropic condition with n = 3.5, m = 1/6, E = 12.5 MPa and Wf = 1 m for various scales of fluctuation

Full size image

Figure 7 shows the variation of the deterministic foundation settlement against the axial stiffness anisotropy ratio for different values of shear stiffness anisotropy ratios and elastic moduli of 12.5 MPa and 50 MPa. Moreover, the variation of the deterministic foundation settlement against the shear stiffness anisotropy ratio is illustrated in Fig. 8. Based on the observations made in these figures, it can be generally concluded that the increase in the anisotropy ratio of elastic modulus, either axial or shear, leads to the remarkable reduction in the total foundation settlement. For instance, the amount of foundation settlement in the case of considerable axial stiffness anisotropy ratio of n = 3.5 decreases to about 40 percent of the estimated settlement corresponding to an isotropic soil state. According to the definition, the increase in axial stiffness anisotropy ratio in a constant vertical elastic modulus (Ev) could be solely attributed to the increase in the elastic modulus in the horizontal plane, highlighting the significant influence of soil lateral stiffness in the evaluation of foundation vertical settlement. It should be also noted that in the case of variation of settlement with shear stiffness anisotropy ratio (\(m\)), as illustrated in Fig. 8, the amount of settlement reduction is higher when \(m\) decreases with respect to the isotropic soil state. As all soils exhibit anisotropic response, these observations could be of great significance in the settlement predictions for the shallow foundations subjected to variable types of loadings.

Fig. 7
figure 7

Variation of deterministic settlement of foundation against the axial stiffness anisotropy ratio for various shear stiffness anisotropy ratios

Full size image
Fig. 8
figure 8

Variation of deterministic settlement of foundation against the shear stiffness anisotropy ratio for various axial stiffness anisotropy ratios

Full size image

Figure 9 shows the typical variation of the standard deviation for the logarithm of foundation settlement against the scale of fluctuation for the log-elastic modulus in an anisotropic soil state for various foundation widths. As can be seen in this figure, very similar to what was observed in the isotropic case, with the increase in the scale of fluctuation of the log-elastic modulus as well as the increase in the variability of the elastic modulus, the soil spatial variability increases, resulting in the higher standard deviation for the logarithm of foundation settlement. Furthermore, it is observed that the decrease in the foundation width could lead to greater values of standard deviation for the log-settlement of the footing, which is due to local averaging.

Fig. 9
figure 9

Variation of the standard deviation of log-settlement of the foundation against the scale of fluctuation of the log-elastic modulus in the case of an anisotropic condition with E = 12.5 MPa, n = 3.5 and m = 1/6 for various foundation widths

Full size image

Figures 10 and 11 illustrate the variations of mean foundation settlement with the coefficient of variation of the elastic modulus in two typical anisotropic soil cases for the unit foundation width and various scales of fluctuation. From the results presented in these figures, it can be observed that the mean total estimated settlement increases with the increase in the variability of elastic modulus irrespective of the assigned values for the scale of fluctuation and degree of soil axial and shear stiffness anisotropies. Moreover, higher values of assigned scale of fluctuation for elastic modulus lead to the greater mean foundation settlements.

Fig. 10
figure 10

Variation of mean foundation settlement against the covariance of elastic modulus in the case of an anisotropic condition with n = 1, m = 1/6, E = 12.5 MPa and Wf = 1 m, for various scales of fluctuation

Full size image
Fig. 11
figure 11

Variation of mean foundation settlement against the covariance of elastic modulus in the case of an anisotropic condition with n = 3.5, m = 1/3, E = 12.5 MPa and Wf = 1 m, for various scales of fluctuation

Full size image

5.2 A pair of spread footings

In the second set of analyses performed in the course of this study, the immediate differential settlement of two adjacent spread footings on an anisotropic and heterogeneous soil layer is investigated. Once again, a typical log-normal distribution is assigned to the soil elastic modulus. Considering the immediate individual settlement of the footings to be δ1 and δ2, the differential settlement of the foundations could be expressed by a log-normal distribution as follows [2]:

$$f_{{\delta_{1} \delta_{2} }} \left( {x,y} \right) = \frac{1}{{2\pi \sigma_{\ln \delta }^{2} rxy}}\exp \left[ { - \frac{1}{{2r^{2} }}\left( {\varPsi_{x}^{2} - \rho_{\ln \delta } \varPsi_{x} \varPsi_{y} + \varPsi_{y}^{2} } \right)} \right],\quad x \ge 0 , y \ge 0$$
(7)
$$\varPsi_{x} = \frac{{lnx - \mu_{ln\delta } }}{{\sigma_{ln\delta } }}$$
(8)
$$\varPsi_{y} = \frac{{lny - \mu_{ln\delta } }}{{\sigma_{ln\delta } }}$$
(9)
$$r^{2} = 1 - \rho_{ln\delta }^{2}$$
(10)

where \(\rho_{ln\delta }\) is the auto-correlation coefficient between the log-settlements of the two footings. It should be noted that the above correlations lie on the assumption of equal mean and variance for δ1 and δ2, which seems to be quite reasonable for the symmetric condition of the model geometry, as depicted in Fig. 2. Expressing the differential settlement between the footings as Δ, its respective governing probability distribution could be presented using the following expression:

$$f_{\Delta } \left( x \right) = \left\{ {\begin{array}{*{20}c} {\mathop \int \limits_{0}^{\infty } f_{{\delta_{1} \delta_{2} }} \left( {x + y,y} \right){\text{d}}y} & {x \ge 0} \\ {\mathop \int \limits_{ - x}^{\infty } f_{{\delta_{1} \delta_{2} }} \left( {x + y,y} \right){\text{d}}y} & {x < 0} \\ \end{array} } \right.$$
(11)

Although there exists no particular analytical solutions for these integrals, they could be explicitly evaluated using various numerical approaches.

Assuming Δ to bear a normal distribution and δ1 and δ2 to follow log-normal distributions with the same auto-correlation coefficients, the following parameters could be associated with the differential settlement of the adjacent footings:

$$\mu_{\Delta } = 0 ,\quad \sigma_{\Delta }^{2} = 2\left( {1 - \rho_{\delta } } \right)\sigma_{\delta }^{2}$$
(12)

Based on the aforementioned definitions, if the scale of fluctuation for the log-elastic modulus, i.e., \(\theta_{lnE}\), tends toward zero, the variance of settlement also approaches zero. On the other hand, as \(\theta_{lnE}\) goes to infinity, the auto-correlation coefficient between the settlements of the two foundations tends toward unity. Consequently, it can be concluded that the differential settlements diminish when the scale of fluctuation is either too large or too small.

The auto-correlation coefficient of the settlement could be quantified using the following formula:

$$\rho_{\delta } = \frac{{\exp \left( {C_{ln\delta } } \right) - 1}}{{\exp \left( {\sigma_{ln\delta }^{2} } \right) - 1}}$$
(13)

where \(C_{ln\delta }\) is the covariance of the log-settlement between the foundations with the width of \(W_{\text{f}}\) and the center-to-center distance of D, which in turn could be estimated using the following correlation:

$$C_{\ln \delta } = \frac{{\sigma_{\ln E}^{2} }}{{W_{\text{f}}^{2} H^{2} }} \mathop \int \limits_{0}^{H} \mathop \int \limits_{0}^{{W_{\text{f}} }} \mathop \int \limits_{0}^{H} \mathop \int \limits_{D}^{{D + W_{\text{f}} }} \rho_{\ln E} \left( {x_{1} - x_{2} , y_{1} - y_{2} } \right) {\text{d}}x_{2} {\text{d}}y_{2} {\text{d}}x_{1} {\text{d}}y_{1}$$
(14)

Figures 12 and 13 show the variations of the auto-correlation coefficient between the footing settlements against the scale of fluctuation for the isotropic and anisotropic soil states beneath the foundations, respectively. As can be observed in these figures, the auto-correlation coefficient follows an ascending trend with the increase in the scale of fluctuation. However, it should be noted that in most of the cases, particularly for the scales of fluctuation ranging from 0.5 to 5, generic scatter could be recognized in the simulation results.

Fig. 12
figure 12

Variation of the auto-correlation coefficient of the differential settlements of the adjacent foundations against the scale of fluctuation for an isotropic soil state with n = 1, m = 1/3, E = 50 MPa and Wf = 1 m

Full size image
Fig. 13
figure 13

Variation of the auto-correlation coefficient for the differential settlements of adjacent foundations against the scale of fluctuation for an anisotropic soil state with n = 3.5, m = 1/2, E = 50 MPa and Wf = 1 m

Full size image

Figures 14 and 15 show the variations of the mean differential settlement of the adjacent footings against the scale of fluctuation for the isotropic and anisotropic soil states, respectively. Based on the observations made from both figures, the mean differential settlement exhibits an ascending trend up to a particular scale of fluctuation of about 2–6, beyond which is followed by a descending trend. In other words, the differential settlement of the adjacent footings bears greater values for the scales of fluctuation ranging from 2 to 6. Similar results are also drawn for the increase in the coefficient of variation of the elastic modulus which leads to the increase in the differential settlement by several orders of magnitude, as presented in Figs. 14 and 15.

Fig. 14
figure 14

Variation of the mean differential settlement of adjacent foundations against the scale of fluctuation for an isotropic soil state with n = 1, m = 1/3, E = 50 MPa and Wf = 1 m

Full size image
Fig. 15
figure 15

Variation of the mean differential settlement of adjacent foundations against the scale of fluctuation for an anisotropic soil state with n = 3.5, m = 1/2, E = 50 MPa and Wf = 1 m

Full size image

6 Concluding remarks

In this study, the significant influence of inherent anisotropy on the immediate total and differential settlement of shallow foundations resting on a heterogeneous soil deposit is thoroughly investigated. To this end, assuming the foundation to be rigid with negligible slippage on the soil beneath, finite element method is combined with several Monte Carlo simulations to perform probabilistic settlement analysis on a single spread footing as well as a pair of shallow foundations. Adopting the modulus of elasticity as the primary random parameter of interest with a typical anisotropic log-normal distribution, several realizations of the shallow foundation settlements are attained, which are then utilized to introduce a general probabilistic model for settlement predictions. Based on the results of numerous probabilistic simulations performed in the course of this study, the following conclusions are drawn:

  1. 1.

    The mean settlement of a single spread footing founded on an isotropic soil stratum increases, up to 25% in some circumstances, with an increase in the coefficient of variation of the soil elastic modulus. The increasing trend of settlement with the coefficient of variation of the elastic modulus follows a linear variation at low scales of fluctuation, but becomes nonlinear at higher values of θ.

  2. 2.

    The increase in the axial and shear stiffness anisotropy ratios of the soil elastic modulus leads to a dramatic reduction in the amount of induced settlement below the single footing. At a given vertical elastic modulus, the increase in the axial stiffness anisotropy ratio could be solely attributed to the increase in the elastic modulus in a horizontal plane which is an evident indicative of the remarkable influence of soil lateral stiffness on the vertical settlement assessment.

  3. 3.

    As the shear stiffness anisotropy ratio (m) increases, the amount of settlement below the foundation decreases. The variations in the amount of settlement are more pronounced when m decreases with respect to the isotropic condition.

  4. 4.

    As the scale of fluctuation for the elastic modulus increases, the discrepancies between the settlement predictions using deterministic and probabilistic approaches become more highlighted.

  5. 5.

    The stiffness anisotropy bears a quite negligible influence on the standard deviation of foundation settlement.

  6. 6.

    The stochastic analysis results in the increase in the settlement evaluation of a single spread footing resting on an anisotropic soil layer.

  7. 7.

    The auto-correlation coefficient between the foundation settlements shows a generic ascending trend with the scale of fluctuation. The aforementioned trend shows a considerable scatter at the low scales of fluctuation ranging from 0.5 to 5, which gradually diminishes as θ increases.

  8. 8.

    The variations of the differential settlements between the adjacent footings against the scale of fluctuation for both isotropic and anisotropic soil states showed that the mean differential settlement bears greater values for the scale of fluctuation ranging from 2 to 6. It is also observed that the increase in the coefficient of variation of the elastic modulus leads to a dramatic increase in the differential settlement of the adjacent footings.