${\mathrm{H}}_{\infty }$ and ${\mathrm{H}}_{2}$ Optimization of the Grounded-Type DVA Attached to Damped Primary System Based on Generalized Fixed-Point Theory Coupled Optimization Algorithm

Abstract

Purpose

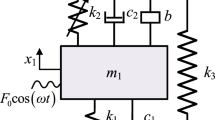
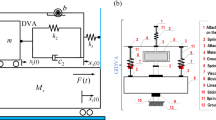
This paper propose a grounded-type DVA attached to a damped primary system, which can effectively suppress the vibration amplitudes by introducing a lever, focusing on the optimal design of the novel DVA. It can be utilized to the simplified model of a damped spacecraft or stay cable of cable-stayed bridges.

Methods

The design of DVA considers ${\mathrm{H}}_{\infty }$ and ${\mathrm{H}}_{2}$ optimization criteria, and defines performance indicators separately. In the ${\mathrm{H}}_{\infty }$ optimization, we couple generalized fixed-point theory (GFPT) and perturbation method (PM) with particle swarm optimization (PSO) algorithm to minimize the maximum amplitude amplification factor of primary system, so that the amplitudes at two fixed points are close to the same horizontal line. Nevertheless, in the ${\mathrm{H}}_{2}$ optimization, the GFPT and PM are combined with Newton’s method to minimize the power input to primary system.

Results

The numerical results indicate the consistency and effectiveness of the two optimization criteria. Compared with other classical models, the effects of different grounded stiffness ratios on the amplitude frequency responses, time histories, and vibration energies of the primary system subjected to harmonic excitation and random excitation, respectively, as well as the vibration reduction effect, are studied.

Conclusions

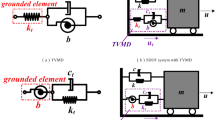
Numerical simulations display with the positive grounded stiffness, the proposed DVA outperform the existing DVAs with same mass, damping, and stiffness under the harmonic excitation and random excitation. The results can provide theoretical and computational guidance for the optimal design of DVA.

Appendices

Appendix A: Symbolic expression

In Sect. 3.1 (Eqs.  (21) and (23)), the expressions of coefficients $a_i$ and $b_i$

$$\begin{aligned} a_{0}&=-\nu _{0}^{8}(1+\alpha )[(1+\alpha )^{3}+\mu L^{2}(1+\alpha -4\xi _{20}^{2})]\\&\quad -\mu \nu _{0}^{10} L^{2}[\alpha (1+\alpha )^{3}+(\alpha (1+\alpha )-2(1+2\alpha )\xi _{20}^{2})\mu L^{2}]\\ a_{1}&=2\nu _{0}^{6}(1+\alpha )[\mu L^{2}+2(1+\alpha )(1+\alpha -2\xi _{20}^{2})]\\&\quad +\nu _{0}^{8}[(1+\alpha )^{4}+(1+2\alpha )\mu ^{2}L^{4}\\&\quad +2(1+\alpha )^{2}\mu L^{2}(1+2\alpha -4\xi _{20}^{2})]\\ a_{2}&=-\nu _{0}^{4}[6(1+\alpha )^{2}+\mu L^{2}-16\mu L^{2}(1+\alpha -\xi _{20}^{2})\xi _{20}^{2}]\\&\quad -\nu _{0}^{6}[\mu ^{2}L^{4}\\&\quad +4(1+\alpha )^{2}(1+\alpha -2\xi _{20}^{2})+\mu L^{2}(5+11\alpha +6\alpha ^{2}\\&\quad -4(3+4\alpha -4\xi _{20}^{2})\xi _{20}^{2})]\\ a_{3}&=2\nu _{0}^{2}[2(1+\alpha -2\xi _{20}^{2})\\&\quad +\nu _{0}^{2}(3(1+\alpha )^{2}+2((1+\alpha )\mu L^{2}\\&\quad -2(2(1+\alpha )+\mu L^{2})\xi _{20}^{2}+4\xi _{20}^{4}))]\\ a_{4}&=-\nu _{0}^{2}[4(1+\alpha )+\mu L^{2}-8\xi _{20}^{2}]-1\\ b_{0}&=2\nu _{0}^{6}\lambda _{1}^{2}(1+\alpha )[\mu L^{2}+2(1+\alpha )(1+\alpha -2\xi _{20}^{2})]\\&\quad -8(1+\alpha )\nu _{0}^{7}\nu _{1}[(1+\alpha )^{3}+\mu L^{2}(1+\alpha -4\xi _{20}^{2})]\\&\quad +\nu _{0}^{8}[\lambda _{1}^{2}((1+\alpha )^{4}\\&\quad +(1+2\alpha )\mu ^{2}L^{4})+2(1+\alpha )\mu L^{2}\\&\quad ((1+\alpha )\lambda _{1}^{2}(1+2\alpha -4\xi _{20}^{2})\\&\quad +4\xi _{20}\xi _{21})]\\&\quad -2\mu \nu _{0}^{9}L^{2}[5\alpha (1+\alpha )\nu _{1}((1+\alpha )^{2}+\mu L^{2})-2(1+\alpha )^{2}\xi _{20}\\&\quad -10(1+2\alpha )\mu \nu _{1}L^{2}\xi _{20}^{2}]+4(1+2\alpha )\mu ^{2}\nu _{0}^{10}L^{4}\xi _{20}\xi _{21}\\ b_{1}&=-2\nu _{0}^{4}\lambda _{1}^{2}[\mu L^{2}+6(1+\alpha )^{2}-16(1+\alpha -\xi _{20}^{2})\xi _{20}^{2}]\\&\quad -16\mu \nu _{0}^{8}(1+\alpha )^{2}L^{2}\xi _{20}\xi _{21}\\&\quad +12(1+\alpha )\nu _{0}^{5}\nu _{1}[\mu L^{2}+2(1+\alpha )(1+\alpha -2\xi _{20}^{2})]\\&\quad +8\nu _{0}^{7}\nu _{1}[(1+2\alpha )\mu ^{2}L^{4}+(1+\alpha )^{4}+2\mu (1+\alpha )^{2}\\&\quad L^{2}(1+2\alpha -4\xi _{20}^{2})]\\&\quad -2\nu _{0}^{6}[4(1+\alpha )^{2}(\lambda _{1}^{2}(1+\alpha -2\xi _{20}^{2})+2\xi _{20}\xi _{21})\\&\quad +\mu \lambda _{1}^{2}L^{2}(5+11\alpha +6\alpha ^{2}+\mu L^{2}-4(3+4\alpha -4\xi _{20}^{2})\xi _{20}^{2})]\\ b_{2}&=12\nu _{0}^{2}\lambda _{1}^{2}(1+\alpha -2\xi _{20}^{2})-4\nu _{0}^{3}\nu _{1}[6(1+\alpha )^{2}\\&\quad +\mu L^{2}-16(1+\alpha -\xi _{20}^{2})\xi _{20}^{2}]\\&\quad +2\nu _{0}^{4}[16(1+\alpha -2\xi _{20}^{2})\xi _{20}\xi _{21}\\&\quad +3\lambda _{1}^{2}(2(1+\alpha )\mu L^{2}+3(1+\alpha )^{2}\\&\quad -4(2(1+\alpha )+\mu L^{2}-2\xi _{20}^{2})\xi _{20}^{2})]-2\nu _{0}^{5}[12\nu _{1}\\&\quad (1+\alpha )^{3}+2\mu L^{2}\xi _{20}\\&\quad +3\nu _{1}(\mu ^{2}L^{4}-8(1+\alpha )^{2}\xi _{20}^{2}+\mu L^{2}(5+11\alpha +6\alpha ^{2}\\&\quad -4(3+4\alpha -4\xi _{20}^{2})\xi _{20}^{2}))]\\&\quad +8\nu _{0}^{6}[2(1+\alpha )^{2}+\mu L^{2}(3+4\alpha -8\xi _{20}^{2})]\xi _{20}\xi _{21}\\ b_{3}&=8\nu _{0}\nu _{1}(1+\alpha -2\xi _{20}^{2})-4\nu _{0}^{2}[\lambda _{1}^{2}(\mu L^{2}\\&\quad +4(-1+\alpha -2\xi _{20}^{2}))+4\xi _{20}\xi _{21}]-4\lambda _{1}^{2}\\&\quad +8\nu _{0}^{3}\nu _{1}[3(1+\alpha )^{2}+2(1+\alpha )\mu L^{2}-4(2+2\xi \\&\quad +\mu L^{2}-2\xi _{20}^{2})\xi _{20}^{2}]\\&\quad -16\nu _{0}^{4}[2(1+\alpha -2\xi _{20}^{2})+\mu L^{2}]\xi _{20}\xi _{21}\\ b_{4}&=5\lambda _{1}^{2}-2\nu _{0}[\nu _{1}(4(1+\alpha )+\mu L^{2})-8(\nu _{1}\xi _{20}+\nu _{0}\xi _{21})\xi _{20}]. \end{aligned}$$

Appendix B: Symbolic expression

In Sect. 3.2 (Eq.  (32)), the coefficient matrix expressions corresponding to the nonlinear equations

$$\begin{aligned}d_{11} & =-\mu (1+2((1+\alpha )^2+\mu \nu ^4(-4\alpha +\mu L^2)L^2\\&\quad +2\nu ^2(2(1+\alpha )(-1+2\xi _1^2)+\mu L^2))\\d_{12} & =\nu ((1+\alpha )^2(-3-16(1+\xi _1^2)\xi _1^2)-8\mu L^2\xi _1^2+4\nu ^2\\&\quad -\nu ^4(1+\alpha )^2((1+\alpha )^2-4\alpha \mu L^2)+\mu ^2(2+3\alpha ^2)L^4\\&\quad -2\nu ^2[-\mu (1+\alpha )(-3\alpha +4(-1+\alpha )\xi _1^2)L^2\\&\quad +4((1+\alpha )^3+\mu ^2L^4)\xi _1^2\\&\quad -2\alpha (3+\alpha (3+\alpha ))])\xi _1\\d_{13} & =\nu ^2(2(1+\alpha )((1+\alpha )^2-2\alpha \mu L^2)\nu ^2\\&\quad +\mu \nu ^4(-1+\alpha ^2(3+2\alpha -2\mu L^2)L^2)\\&\quad +2(1+\alpha )^2(-1+4(-3+\nu ^2(1+\alpha )-4\xi _1^2)\xi _1^2)\\&\quad +8\nu (-1+\nu ^2(-1+\alpha (2+3\alpha )-\mu L^2)-2\xi _1^2)L^2\xi _1^2)\\d_{14} & =8\nu ^3((1+\alpha )^2(1-2\xi _1^2)+\mu (\nu ^2(-1+\alpha ^2)-4\xi _1^2)L^2)\xi _1\\d_{15} & =-16\mu \nu ^4L^2\xi _1^2\\d_{21} & =-2\mu \nu ((1+\alpha )\nu ^2+4\xi _1^2)L^2\xi _1\\d_{22} & =\nu ^4(-(1+\alpha )^3+\alpha \mu (2(1+\alpha )-\mu L^2)L^2)\\&\quad -(1+\alpha )(1+4(-3+4\xi _1^2)\xi _1^2)\\&\quad -\nu ^2(2(1+\alpha )^2(-1+4\xi _1^2)+\mu (1+2\alpha +4(2-3\alpha )\xi _1^2)L^2)\\d_{23} & =-8\nu (2(1+\alpha )(-1+2\xi _1^2)-\nu ^2((1+\alpha )^2-2\alpha \mu L^2))\xi _1\\d_{24} & =4\nu ^2(\alpha \mu \nu ^2L^2+(1+\alpha )(1-4\xi _1^2))\\d_{31} & =-\mu ^2\nu ^5(-1+\alpha (3+4\alpha )+\nu ^2(8\alpha (1+\alpha )^2(-1+2\xi _1^2)\\&\quad +\mu (1+6\alpha +8\alpha ^2)L^2)\\&\quad +\alpha \nu ^4(4(1+\alpha )(1+\alpha )^2-2\alpha \nu L^2\\&\quad +\mu ^2(3+4\alpha )L^4))L^4\xi _1^2\\d_{32} & =-2\mu \nu ^2(\alpha \nu ^8((1+\alpha )^5-\mu (1+\alpha )\\&\quad ((1+\alpha )(1+2\alpha ^2)-4)L^2\\&\quad +\alpha \mu ^3(-2(1+2\alpha )+\mu L^2)L^6)\\&\quad +\nu ^6(2\alpha \mu ^2(-2+2\alpha (-3(1+\alpha )+\mu L^2)\\&+2(3+3\alpha (3+\alpha ))\xi _1^2+\mu L^2)L^4\\&\quad +4\alpha (1+\alpha )^4(-1+2\xi _1^2)\\&\quad -\mu (1+\alpha )^2(-1+2\alpha (-1-6\alpha +4(-1+2\alpha )\xi _1^2))L^2)\\&\quad +\nu ^4((1+\alpha )^3(-1+2\alpha (3-8(1-\xi _1^2)\xi _1^2))\\&\quad +\mu ^2(1+6\alpha (1+\alpha ))L^4\\&\quad +2\mu (1+\alpha )(-1-3\alpha (1+2\alpha )\\&\quad +2(1+2\alpha (3+2\alpha )\xi _1^2)L^2))\\&\quad +2\nu ^2((1+\alpha )(-1+2\xi _1^2)+\mu (1+2\alpha )L^2)\\&\quad +1+\alpha (2+\alpha ))L^2\xi _1\\d_{33} & =-\mu \nu ^2(3\alpha \mu \nu ^8((1+\alpha )^3+\alpha \mu (-2(1+\alpha +\mu L^2))L^2)\\&\quad +\nu ^6((1+\alpha )^4+\alpha \nu (-12(1+\alpha )^2+\mu (6+11\alpha )L^2)L^2\\&\quad +4\alpha (2(1+\alpha )^2(2(1+\alpha )^2+\mu (3-2\alpha )L^2)\\&\quad +4\mu ^2(6+\alpha (9-4(\alpha -\mu L^2)))L^4)\xi _1^2)\\&\quad +\nu ^4(2(1+\alpha )^3(-3+32\alpha \xi _1^4)\\&\quad +(1+\alpha )\mu (3+13\alpha +16\alpha (3+4\alpha )\xi _1^4)L^2\\&\quad +8(-(1+\alpha )^3(1+2\alpha )\\&\quad -\mu ((\alpha ^2-1)(1+4\alpha )+2\alpha \mu (2+3\alpha )L^2)\xi _1^2))\\&\quad +16(1+\alpha )^2\xi _1^2\\&+\nu ^2(1+\alpha )((1+\alpha )(5-4(3+4\alpha )\xi _1^2+16(1+4\alpha )\xi _1^4)\\&\quad +16\mu (1+3\alpha )L^2\xi _1^2))L^2\\d_{34} & =-8\mu \nu ^4(\alpha \mu \nu ^6(3+\alpha (8+\alpha (7+2\alpha )\\&\quad +2\mu (-2\alpha +\mu L^2)L^2))L^2\\&\quad +\nu ^4((1+\alpha )^3(1+\alpha (2+4\xi _1^2))\\&\quad +2\alpha \mu (\mu (2+\alpha (3+2\xi _1^2))L^2\\&\quad +2(1+\alpha )(-2\alpha +(3+4\alpha )\xi _1^2))L^2)\\&\quad +2(1+\alpha )^2(1+2\xi _1^2)\\&\quad +2\nu ^2(1+\alpha )(2(1+\alpha )(\xi _1^2+\alpha (-1+4\xi _1^2))\\&\quad +\mu (1+\alpha (3+4\xi _1^2))L^2))L^2\xi _1\\d_{35} & =-4\mu \nu ^5(3\nu ^2(1+\alpha +\alpha \mu \nu ^2L^2)^2\\&\quad +4(\alpha \mu \nu ^4(3+\alpha (7+4\alpha +4\mu L^2))L^2 \\&\quad +4(1+\alpha )^2+\nu ^2(1+\alpha )\\&\quad (1+\alpha (5+4\alpha +8\mu L^2)))\xi _1^2)L^2\\d_{36} & =-32\mu \nu ^6(1+\alpha +\alpha \mu \nu ^2L^2)^2L^2\xi _1. \end{aligned}$$