Dynamic Analysis of a Three-Layered Sandwich Plate with Composite Layers and Leptadenia Pyrotechnica Rheological Elastomer-Based Viscoelastic Core

Abstract

Purpose

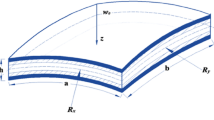
The three-layered sandwich plate with thin composite skins and leptadenia pyrotechnica rheological elastomer (LPRE) core is used to reduce the vibration in the structural system.

Method

The governing equation of motion for the composite sandwich plate is obtained by the Lagrange principle based on first order shear deformation theory and presented in the finite element form. The natural frequencies and loss factors of the system have been obtained by finding the eigenvalues of the dynamic matrix. Further forced vibration response has been obtained. For numerical analysis, experimentally obtained mechanical properties of the LPRE core are used in this investigation.

Results and Conclusions

The natural frequencies and loss factors of the LPRE-based sandwich plate are determined by varying the thicknesses of the core and the constraining composite layers with five boundary conditions. The results are compared with those of similar structures with different core materials and boundary conditions and are found to be in good agreements. The forced vibration response of the three-layered composite sandwich plate is also investigated in the presence of harmonic excitation force. The natural frequencies and loss factors of LPRE-based composite sandwich plate are compared with LPRE-based isotropic sandwich plate (Ojha et al., Int J Struct Stab Dyn 19(3):81048, 2019). It is found that the fundamental frequency of the LPRE-based composite sandwich plate are almost 1.90 times higher than the LPRE-based isotropic sandwich plate even if the composite sandwich plate has 45% lesser weight than the isotropic sandwich plate. The loss factors of the LPRE composite sandwich plate are also more than the LPRE isotropic sandwich plate. This study supports the application of the LPRE-based sandwich plates with composite skins potentially to the passive vibration suppression of the structural systems.

Appendix

The elemental mass and stiffness matrices are given as

$$\left[ {M^{\text{e}} } \right] = \left[ {M_{\text{u,v}}^{(2i - 1)} } \right] + \left[ {M_{\text{shear}}^{(2i)} } \right] + \left[ {M_{\text{w}}^{(2i - 1)} } \right] + \left[ {M_{\text{w}}^{(2i)} } \right],$$

$$\left[ {M_{\text{u,v}}^{(2i - 1)} } \right] = \sum\limits_{i = 1}^{l + 1} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\rho_{(2i - 1)} } } h_{(2i - 1)} \left( {\left[ {N_{u(2i - 1)} } \right]^{T} \left[ {N_{u(2i - 1)} } \right] + \left[ {N_{v(2i - 1)} } \right]^{T} \left[ {N_{v(2i - 1)} } \right]} \right){\text{d}}x{\text{d}}y} ,$$

$$\left[ {M_{\text{shear}}^{(2i)} } \right] = \sum\limits_{i = 1}^{l} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\rho_{(2i)} \frac{{h_{(2i)}^{3} }}{12}} } \left( {\left[ {N_{\text{xz}} } \right]^{T} \left[ {N_{\text{xz}} } \right] + \left[ {N_{\text{yz}} } \right]^{T} \left[ {N_{\text{yz}} } \right]} \right){\text{d}}x{\text{d}}y,}$$

$$\left[ {M_{\text{w}}^{(2i - 1)} } \right] = \sum\limits_{i = 1}^{l + 1} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\rho_{(2i - 1)} } } h_{(2i - 1)} \left( {\left[ {N_{\text{w}} } \right]^{T} \left[ {N_{\text{w}} } \right]} \right){\text{d}}x{\text{d}}y} ,$$

$$\left[ {M_{\text{w}}^{(2i)} } \right] = \sum\limits_{i = 1}^{l} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\rho_{(2i)} } } h_{(2i)} \left( {\left[ {N_{\text{w}} } \right]^{\text{T}} \left[ {N_{\text{w}} } \right]} \right){\text{d}}x{\text{d}}y} ,$$

$$\left[ {K^{\text{e}} } \right] = \left[ {K_{(2i - 1)}^{\text{e}} } \right] + \left[ {K_{(2i)}^{\text{e}} } \right],$$

$$\left[ {K_{(2i - 1)}^{\text{e}} } \right]{ = }\sum\limits_{i = 1}^{l + 1} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\left\{ {\varepsilon_{0(2i - 1)} } \right\}^{\text{T}} \left[ \begin{aligned} \, \left[ A \right]_{(2i - 1)} \, \left[ B \right]_{(2i - 1)} \hfill \\ \, \left[ B \right]_{(2i - 1)} \, \left[ D \right]_{(2i - 1)} \, \hfill \\ \end{aligned} \right]} } } \left\{ {\varepsilon_{0(2i - 1)} } \right\}{\text{d}}x{\text{d}}y,$$

$$\left\{ {\varepsilon_{0(2i - 1)} } \right\}^{T} = \left[ {\left[ {\frac{{\partial N_{u(2i - 1)} }}{\partial x}} \right]\left[ {\frac{{\partial N_{v(2i - 1)} }}{\partial y}} \right]\left[ {\frac{{\partial N_{u(2i - 1)} }}{\partial y} + \frac{{\partial N_{v(2i - 1)} }}{\partial x}} \right] - \left[ {\frac{{\partial^{2} N_{w} }}{{\partial x^{2} }}} \right] - \left[ {\frac{{\partial^{2} N_{w} }}{{\partial y^{2} }}} \right] - \left[ {2\frac{{\partial^{2} N_{w} }}{\partial x\partial y}} \right]} \right],$$

$$\left[ {K_{(2i)}^{\text{e}} } \right] = \sum\limits_{i = 1}^{l} {\int\limits_{{\frac{ - a}{2}}}^{{\frac{a}{2}}} {\int\limits_{{\frac{ - b}{2}}}^{{\frac{b}{2}}} {\left\{ \begin{aligned} \left[ {N_{xz}^{(2i)} } \right] \hfill \\ \left[ {N_{yz}^{(2i)} } \right] \hfill \\ \end{aligned} \right\}} }^{T} \left[ \begin{aligned} Gh_{\text{c}}^{(2i)} { 0} \hfill \\ 0 \, Gh_{\text{c}}^{(2i)} \hfill \\ \end{aligned} \right]\left\{ \begin{aligned} \left[ {N_{\text{xz}}^{(2i)} } \right] \hfill \\ \left[ {N_{\text{yz}}^{(2i)} } \right] \hfill \\ \end{aligned} \right\}{\text{d}}x{\text{d}}y} ,$$

$$\left[ {N_{\text{xz}}^{(2i)} } \right] = \frac{1}{{h_{(2i)} }}\left[ {\left( {\left[ {N_{u(2i - 1)} } \right] - \left[ {N_{u(2i + 1)} } \right]h_{e} \left[ {\frac{{\partial N_{w} }}{\partial x}} \right]} \right) + } \right],$$

$$\left[ {N_{\text{yz}}^{(2i)} } \right] = \frac{1}{{h_{\text{c}}^{(2i)} }}\left[ {\left( {\left[ {N_{v(2i - 1)} } \right] - \left[ {N_{v(2i + 1)} } \right]} \right) + h_{\text{e}} \left[ {\frac{{\partial N_{\text{w}} }}{\partial y}} \right]} \right].$$