1 Introduction

The commercial air transport industry has a strong resistance to external shocks and is one of the fastest-growing industries in the world. From 1988 to 2018, despite the impact of war, epidemic and financial crisis, the global annual air traffic (RPK) still doubled every 15 years [1]. Although the global air traffic volume has declined sharply since 2020 due to the impact of COVID-19, the air traffic will return to the level of 2019 from 2023 to 2025, according to the global market forecast released by Airbus in 2022. With the future increase in air traffic demand, air passenger traffic volume will increase by 3.6% CAGR, and air freight traffic volume will increase by 3.2% CAGR, from 2019 to 2041. The number of aircraft operated worldwide will increase from 22,880 in 2020 to 46,930 in 2041. The global civil aviation market is expected to require 39,490 new aircraft, of which 24,050 are used to meet the growing air traffic demand [2]. At the same time, the population living in cities is increasing. According to the statistics of the UN DESA, 55% of the world's population lived in urban areas in 2018, which is expected to reach 68% by 2050 [3]. The expansion of urban areas inevitably leads to the extension of urban residential space to the vicinity of airports, which were originally located in the suburbs. Nowadays, more and more residents are suffering from civil aviation noise due to the new construction and expansion of urban airports, as well as the airport surrounding planning that does not fully consider aircraft noise. Aviation noise pollution around airports has become a serious social problem.

The World Health Organization (WHO) believes that noise pollution is the second largest environmental risk factor after air pollution [4], while aviation noise is one of the three major traffic noises, second only to road traffic and railway traffic noise [5]. Aviation noise refers to the noise generated during aircraft flight, including the noise generated by the engine, airframe, landing gear, high lift device and other components [6]. Aviation noise damage plays a dominant role in the per-person expected environmental impact within 6 km around the airport [7]. Relevant medical research shows that long-term exposure to aviation noise will lead to annoyance, sleep disorder [8], and increase the risk of cardiovascular diseases (hypertension, coronary heart disease, heart failure, etc.) [9,10,11,12]. Not only that, aviation noise will hinder the development of children's learning ability and cognitive skills [13], and may even lead to children's mental health problems [14,15,16].

The history of the civil aviation transportation industry has confirmed that aviation noise pollution is one of the main obstacles to the sustainable development of the industry. On the one hand, excessive aviation noise emissions will lead to complaints from surrounding communities and may turn into conflicts. Such incidents have occurred in Britain, Japan, Greece and many other countries. On the other hand, it will also lead to the loss of social wealth. Aircraft noise has a negative impact on house prices within 10 km of the airport. An increase of 1 dB (A) DNL in noise pollution will reduce the value of the property by 0.5%. From 2006 to 2017, the sales loss of the property near Minneapolis-Saint Paul International Airport reached 167 million dollars [17]. If London Heathrow Airport is expanded, it will cause noise loss of 92.5 million to 104.6 million pounds in 2030 [18]. In 2015, the social cost of aviation noise caused by the operation of Taipei Songshan Airport reached 33 million euros [19].

The research on metrics and prediction methods of aviation noise will help us better understand how aviation noise brings negative impacts on individuals, society and the environment, so as to control and reduce aviation noise. The ultimate goal is to promote the sustainable development of the aviation industry by building the “Green Airport”. The structure of this review is as follows. Section 2 summarizes three types of aviation noise metrics: single event noise metrics, cumulative exposure metrics, and daily noise metrics, and makes in-depth analysis on the basis of explaining their characteristics. Section 3 describes three kinds of aviation noise prediction models: best practice model, scientific model and machine learning model, explains their modeling ideas and summarizes relevant academic research results. Section 4 introduces the commonly used noise prediction software and gives the access address. Section 5 puts forward challenges and prospects, and Sect. 6 is the conclusion.

2 Noise Metrics

2.1 Common Noise Metrics

The noise metric is greatly affected by the economy, culture, society, history, technical level of the aviation industry and other factors in different countries or regions. About 25 years ago, different countries used different noise metrics, but now the situation is changing. Taking Europe as an example, the Noise and Number Index (NNI) metric used in the UK since the 1960s was replaced by the \({L}_{Aeq}\) metric in 1990. The Kosten index (\({K}_{e}\)) metric, founded on the \({L}_{Amax}\) metric, was used in the Netherlands until it was replaced by the \({L}_{{\mathrm{den}}}\) metric in February 2003. While the Psophic index (IP) metric based on the Perceived Noise Level (PNL) scale was used in France before it was replaced by the \({L}_{{\mathrm{den}}}\) metric in 2002 [20]. To facilitate environmental noise reporting and mapping in the EU area, Directive 2002/49/EC issued by the European Parliament requires all member states to use the \({L}_{{\mathrm{den}}}\) and \({L}_{{\mathrm{night}}}\) metrics with a 24-h cycle, but it also recommends that supplementary noise metrics should be used when (1) The working time of the noise source is very short; (2) The average number of noise events is very low; (3) The low-frequency component of noise is very strong; (4) Noise has impact; (5) Additional restrictions are required on weekends or specific time periods of the year/daytime/nighttime, and other special circumstances [21].

Table 1 lists the main aircraft noise metrics used by some countries before and now.

Table 1 Noise metrics in different countries
Full size table

2.2 Classification of Noise Metrics

It is very complicated to define a noise metric. A noise metric shall include at least one or more factors, such as (1) Sound level; (2) The frequency or pitch of the sound; (3) Duration of the sound; (4) Number of noise events; (5) Time of day (daytime/evening/nighttime). It is the basic factors contained in the noise metric that determine its characteristics. Thus, a noise metric may belong to several different categories simultaneously.

The classification of noise metrics depends on the constituent factors of metrics, the physical characteristics of noise, people's subjective feelings and so on. Therefore, there is no unified standard in the world. Generally speaking, noise metrics can be divided into three categories: single event noise metrics, cumulative exposure metrics and daily metrics (Table 2).

Table 2 Classification of noise metrics
Full size table

2.2.1 Single Event Noise Metrics

The single event noise metric describes the noise impact caused by the movement or overflight of a single aircraft according to invasiveness, loudness and noisiness. Common single event noise metrics include \({L}_{Amax}\), \({L}_{AFmax}\), \({L}_{ASmax}\), etc., which reflect the maximum sound pressure level (SPL) caused by noise, and \({L}_{{\mathrm{E}}}\), \({L}_{AE}\), etc., which reflect the noise dose in a single event.

  1. 1.

    A-weighted maximum sound level (\({L}_{Amax}\))

To explain the \({L}_{Amax}\) metric, it is necessary to first explain the concepts of sound pressure and sound pressure level. Sound pressure is the pressure exerted by sound waves, and its unit is Pascal (\({\mathrm{p}}_{\mathrm{a}}\)). The sound pressure level is the ratio of actual sound pressure to reference sound pressure, and its unit is the decibel (dB). The calculation formula for sound pressure level is as follows.

$${L}_{{\mathrm{p}}}=10{\mathrm{log}}_{10}\frac{{p}^{2}}{{p}_{0}^{2}}=20{\mathrm{log}}_{10}\frac{p}{{p}_{0}},$$
(1)

where \(p\) is the measured root-mean-square sound pressure, \({p}_{0}\) is the reference sound pressure, and its value is 20 \(\upmu {\mathrm{p}}_{\mathrm{a}}\) (in the air). The sound reference pressure is the threshold of human hearing (in the air) when the sound frequency is 1 kHz.

The human ear is sensitive to sound frequencies between 500 Hz and 6 kHz, especially around 4 kHz. A-weighting weakens the sound value measured at low and high frequencies and emphasizes the sound value measured at middle frequencies. Therefore, the adjusted result can better reflect the sound actually heard by human ears [30]. In contrast, Z-weighting represents Zero-weighting, which is the actual level of the sound measured. The A-weighting and Z-weighting curves are shown in Fig. 1. The sound pressure level adjusted by the A-weighted method has a good correlation with the subjective response in the normal sound pressure level range, which is generally written as \({L}_{A}\). Meanwhile, this adjustment method is applicable to aviation activities and general environmental acoustics, so it is widely used.

Fig. 1
figure 1

A-weighting and Z-weighting curves

Full size image

The sound pressure level of noise changes very fast, while the sound level meter samples the noise with millisecond accuracy. Thus, in addition to frequency weighting, time weighting is also needed to make the measured noise data readable. The commonly used time weighting methods are Fast weighting and Slow weighting. Their time constants are 0.125 s and 1 s, respectively. They both inhibit the response of display level to sudden changes in sound level, but the difference is that Fast weighting reacts faster to the rise and fall of sound level than Slow weighting. In the study of aviation noise, unless the time weighting method is indicated, such as \({L}_{ASmax}\), Fast weighting will be used by default, such as \({L}_{Amax}\).

The \({L}_{Amax}\) metric refers to the maximum value of \({L}_{A}\) measured by the Fast weighting method when the aircraft flies over, and the unit is dB (A). Its calculation formula is as follows according to ISO 1996-1 standard [22].

$${L}_{Amax}=\mathrm{max}\left({L}_{A}\right).$$
(2)

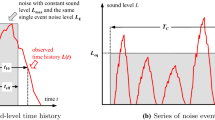
It can be seen from Fig. 2 that the \({L}_{Amax}\) metric has two major shortcomings: (1) It only describes the instantaneous sound pressure intensity of noise events without considering the cumulative sound energy. In fact, when the maximum A-weighted sound level is the same, the events with greater cumulative sound energy are more unbearable. (2) It cannot reflect the number of noise events. Within a certain time interval, no matter how many times noise events with the same A-weighted maximum sound level occurs, the value of \({L}_{Amax}\) will not change.

  1. 2.

    Sound exposure level \({L}_{{\mathrm{E}}}\)

Fig. 2
figure 2

A-weighted maximum sound level diagram

Full size image

The sound exposure level is a metric for measuring the total energy of a noise event within a specific time interval (usually 1 s), expressed in dB. The calculation formula for the \({L}_{{\mathrm{E}}}\) metric is as follows according to ISO 80000-8 standard [23].

$${L}_{{\mathrm{E}}}=10{\mathrm{log}}_{10}\frac{E}{{E}_{0}},$$
(3)
$$E=\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}{p}^{2}\left(t\right)dt,$$
(4)

where \(E\) represents sound exposure, and its unit is \({\mathrm{Pa}}^{2}\, \mathrm{s}\). It can be seen from formula (4) that the value of sound exposure is equal to the integral of the instantaneous frequency-weighted square sound pressure in a given time interval (\({t}_{1}\)–\({t}_{2}\)). The value of reference sound exposure \({E}_{0}\) depends on the weighting or correction method of sound exposure \(E\). If sound exposure \(E\) uses A-weighting, \({E}_{0}\) is equal to \(400\,\upmu \mathrm{P}{\mathrm{a}}^{2}\, \mathrm{s}\). If sound exposure \(E\) uses tone correction in Federal Aviation Regulation Part 36 to consider pure tones or other major irregularities in the aircraft noise spectrum, \({E}_{0}\) is equal to \(4000\,\upmu \mathrm{P}{\mathrm{a}}^{2}\, \mathrm{s}\). Standard IEC 61672-1 stipulates that if the sound is weighted by a specific frequency, the appropriate subscript shall be used [31]. For example, the \({L}_{AE}\) metric is the average A-weighted sound level of energy within the interval of one second.

Obviously, the \({L}_{AE}\) metric solved the first shortcoming of the \({L}_{Amax}\) metric. As shown in the red area in Fig. 3, the \({L}_{AE}\) metric does not consider the instantaneous sound pressure but compresses the cumulative sound energy generated by a single noise event to 1 s, so this metric can be used to measure different events. In addition, when evaluating the same noise event, the value of \({L}_{AE}\) is always greater than that of \({L}_{Amax}\), because the duration of the aircraft noise event is always longer than 1 s.

Fig. 3
figure 3

A-weighted sound exposure level diagram

Full size image

When the \({L}_{AE}\) and \({L}_{Amax}\) metrics are used together, the noise level of a single event can be comprehensively evaluated.

2.2.2 Cumulative Exposure Metrics

Cumulative exposure metrics are used to quantify the noise impact caused by the movement of multiple aircraft within a given time range, so these metrics are usually complex. Common cumulative exposure metrics include \({L}_{eqT}\), \({L}_{AeqT}\), \({L}_{{\mathrm{day}}}\), \({L}_{{\mathrm{evening}}}\), \({L}_{{\mathrm{night}}}\), etc., which reflect the equivalent sound level, and \({L}_{{\mathrm{den}}}\)-CNEL, \({L}_{dn}\), \({L}_{{\mathrm{den}}}\), etc., which represent the combined sound level.

  1. 1.

    Equivalent continuous sound level \({L}_{eqT}\)

The \({L}_{eqT}\) metric measures the average sound pressure level in a certain time interval, which can be used to evaluate the cumulative effect of all noise events occurring in the reference time interval. Similarly, \({L}_{AeqT}\) is the A-weighted equivalent continuous sound level, generally written as \({L}_{Aeq,T}\). The \({L}_{Aeq,T}\) metric can well reflect the community troubles caused by aircraft noise [32], so it has become the most widely used international noise metric. The US EPA takes it as the basic noise measurement description metric. WHO uses this metric to assess the health impact caused by noise. In addition, the FAA, the EU, and most aviation management organizations are using cumulative exposure metrics, including the \({L}_{AeqT}\) metric.

The calculation formula for the \({L}_{Aeq,T}\) metric is as follows according to ISO 1996-2 [24] and ISO 20906 standard [25].

$${L}_{Aeq,T}=10{\mathrm{log}}_{10}\frac{\frac{1}{T}{\int }_{{t}_{1}}^{{t}_{2}}{p}_{A}^{2}\left(t\right)dt}{{p}_{0}^{2}},$$
(5)

where \({p}_{A}\left(t\right)\) is the A-weighted instantaneous sound pressure of running time (\({t}_{1}{-}{t}_{2}\)), the sound reference pressure \({p}_{0}\) equals \(20\,\upmu\mathrm{Pa}\). T is the average time of daytime, evening and nighttime, which needs to be adjusted according to different regions.

The \({L}_{Aeq,T}\) metric solves two shortcomings of the \({L}_{Amax}\). Figure 4 is the schematic diagram of \({L}_{Aeq,T}\). The area of the red area in the figure is equal to the area of the blue area, that is, \({L}_{Aeq, T}\) metric averages the sound energy of the noise events to the measurement time period T. According to different scenarios, T can be set to 1 s, 24 h, or 1 year, etc. For example, when T is 0.125 s, \({L}_{Aeq, 0.125s}\) is equivalent to \({L}_{Amax}\). Note that there is no comparability between the \({L}_{Aeq,T}\) metric with different T values, so the value of T must be indicated when using.

  1. 2.

    Day–evening–night noise level \({L}_{{\mathrm{den}}}\)

Fig. 4
figure 4

A-weighted equivalent continuous sound level diagram

Full size image

The \({L}_{{\mathrm{den}}}\) metric is a combined metric based on the equivalent continuous sound level \({L}_{Aeq,T}\), as shown in Fig. 5. It combines the \({L}_{{\mathrm{day}}}\) metric, the \({L}_{{\mathrm{evening}}}\) metric, the \({L}_{{\mathrm{night}}}\) metric, and adds 5 dB (A), 10 dB (A) to the values of \({L}_{{\mathrm{evening}}}\), \({L}_{{\mathrm{night}}}\) as penalty parameters, respectively. The calculation formula for the \({L}_{{\mathrm{den}}}\) metric is as follows according to Directive 2002/49/CE [21] and Advisory Circular 150/5020–1 [26].

$${L}_{{\mathrm{den}}}=10{\mathrm{log}}_{10}\left[\frac{1}{24}\left(12\cdot {10}^{\frac{{L}_{{\mathrm{day}}}}{10}}+4\cdot {10}^{\frac{{L}_{{\mathrm{evening}}}+5}{10}}+8\cdot {10}^{\frac{{L}_{{\mathrm{night}}}+10}{10}}\right)\right],$$
(6)

where \({L}_{{\mathrm{day}}}\), \({L}_{{\mathrm{evening}}}\) and \({L}_{{\mathrm{night}}}\) are the A-weighted long-term average sound levels during the daytime (7:00–19:00), evening (19:00–23:00) and nighttime (23:00–7:00) of the year. The calculation formulas for the \({L}_{{\mathrm{day}}}\) metric, the \({L}_{{\mathrm{evening}}}\) metric, the \({L}_{{\mathrm{night}}}\) metric are as follows.

$${L}_{{\mathrm{day}}}=10{\mathrm{log}}_{10}\left(\frac{1}{12}\cdot \sum_{H=7}^{18}{10}^{\frac{{L}_{Aeq,H}}{10}}\right),$$
(7)
$${L}_{\mathrm{evening}}=10{\mathrm{log}}_{10}\left(\frac{1}{4}\cdot \sum_{H=19}^{22}{10}^{\frac{{L}_{Aeq,H}}{10}}\right),$$
(8)
$${L}_{\mathrm{night}}=10{\mathrm{log}}_{10}\left(\frac{1}{8}\cdot \sum_{H=23}^{6}{10}^{\frac{{L}_{Aeq,H}}{10}}\right),$$
(9)

where \(H\) is the index for the hours of the day, for example, when \(H\) is equal to 6, it represents the hour from 6:00 to 6:59:59. The \({L}_{Aeq,H}\) is the \({L}_{Aeq,T}\) in the hour \(H\). Note that, as mentioned earlier, different regions may have different definitions of the start and end time points of daytime, evening and nighttime. It is necessary to consult relevant local regulations before using these metrics.

Fig. 5
figure 5

Day–evening–night noise level diagram

Full size image

The calculation formula of CNEL and \({L}_{dn}\) is similar to that of \({L}_{{\mathrm{den}}}\). The difference is that in the CNEL metric, the evening is defined as 19:00–22:00, and the night is defined as 22:00–7:00. The penalty parameter of CNEL for the evening noise is 4.78 dB (A), which is equivalent to the flight noise impact of 3 days, while the penalty parameter of \({L}_{{\mathrm{den}}}\) for the evening noise is 5 dB (A), which is equivalent to the flight noise impact of 3.162 days. The calculation formula for CNEL is as follows.

$$\mathrm{CNEL}=10{\mathrm{log}}_{10}\left[\frac{1}{24}\left(12\cdot {10}^{\frac{{L}_{{\mathrm{day}}}}{10}}+3\cdot {10}^{\frac{{L}_{{\mathrm{evening}}}+4.78}{10}}+9\cdot {10}^{\frac{{L}_{{\mathrm{night}}}+10}{10}}\right)\right].$$
(10)

The day–night equivalent sound level \({L}_{dn}\) divides the day into two time periods: daytime (7:00–22:00) and nighttime (22:00–7:00). FAA stipulates that only areas around the airport with noise levels below the 65 dB (A) DNL threshold can be used for residential construction. The calculation formula for the \({L}_{dn}\) is as follows.

$${L}_{dn}=10{\mathrm{log}}_{10}\left[\frac{1}{24}\left(15\cdot {10}^{\frac{{L}_{{\mathrm{day}}}}{10}}+9\cdot {10}^{\frac{{L}_{{\mathrm{night}}}+10}{10}}\right)\right].$$
(11)

\({L}_{{\mathrm{den}}}\), \({L}_{dn}\) and CNEL have been widely accepted as single digital metric to evaluate the impact of long-term environmental noise. However, the 10 dB (A) penalty parameter for night events is often questioned. In addition, some scholars believe that these metrics do not fully explain the impact of pure tone and isolated loud noise events.

2.2.3 Daily Noise Metrics

Hooper et al. [33] found that the above metrics used for supervision or approval are too specialized, which are not convenient for use in daily life. Therefore, relevant scholars began to put forward daily noise metrics with low professional level, such as Number Above (NA): refers to the number of flights exceeding the specified noise level threshold in an area [34]; Time Above (TA): measures the total time or percentage of time when the sound pressure level generated by the aircraft exceeds the given threshold [35]; Person Events Index (PEI): the total number of aviation noise events that individuals are exposed to exceeding the specified noise threshold based on the exposed population [20].

One of the most famous metrics is the Harmonica index [29]. It is a dimensionless noise metric that aims to provide information on noise that is closer to what people perceive. The unit of the Harmonica index does not use dB (A), which is not familiar to community residents [36], but uses the 0–10 scale obtained by converting the measured value of \({L}_{Aeq,1s}\). As shown in Fig. 6, the Harmonica index consists of two parts: the rectangle represents the environmental background noise level, and the triangle above the rectangle represents the event noise level. The non-profit environmental organization Bruitparif supplements the Harmonica index with three colors, i.e., the green, the orange and the red, which are used to represent low noise, loud and very loud, respectively.

Fig. 6
figure 6

Schematic diagram of harmonica index

Full size image

3 Aviation Noise Prediction Method

The noise prediction model combines the algorithm and related database, in which the algorithm describes the generation, emission and propagation of noise, and the database provides all the information required by the algorithm. Reliable noise prediction models can be applied to the development of noise abatement procedures or the design and manufacture of aircraft to reduce noise [37]. The types of algorithms range from relatively simple empirical models to complex methods trying to reflect the underlying physics. Different types of algorithms have different requirements for the database. Generally, aviation noise assessment methods can be divided into three categories: best practice model, scientific model [38] and machine learning model.

3.1 Best Practice Model

The best practice model is used to predict the noise generated under complex air traffic conditions, rather than the noise of a single aircraft operation. All the best practice models describe the aircraft as a simple noise point source without considering the specific sound mechanism (engine noise, airframe noise, aerodynamic noise, etc.), so it has strong universality and is the most widely used model in the world. After reasonable correction and actual measurement verification, reliable noise prediction results can be obtained, and the model can be applied to noise legislation after standardization. Therefore, the prediction results usually directly affect practical activities such as land use plans, construction of sound insulation facilities and payment of noise compensation costs [39]. The first version of the AzB model proposed the closest point of approach (CPA) in 1975, which determines the noise level based on the nearest distance between the track and the monitoring point [40]. The CPA has been gradually replaced by the trajectory segmentation model since the 1980s, which divides the trajectory into several segments, and then calculates the comprehensive noise impact of each segment on the ground monitoring points, as shown in Fig. 7a.

Fig. 7
figure 7

Schematic diagram of trajectory segmentation method and NPD curve

Full size image

Now, the Noise–Power–Distance (NPD) curve based on the trajectory segmentation method is the most common. This method assumes that the aircraft flies at constant power, and the noise level is a function of the vertical distance on an infinite straight trajectory. It can be seen from Fig. 7b that the corresponding Sound Exposure Level (SEL) noise value can be obtained by determining the distance between the aircraft and the monitoring point and the current engine thrust of the aircraft. In practical application, some corrections need to be supplemented, such as duration correction, finite segment correction, directivity correction, and engine installation correction [41].

The best practice model is based on dynamics and also requires airport data (such as the number and direction of runways), geographic database and meteorological database, etc. The database shall at least be applicable to the current mainstream aircraft models and provide clear model replacement rules. Torija et al. [42] are committed to improving the computational efficiency of the model. Considering the complex composition of the British commercial aircraft fleet, they simplified the fleet into four representative-in-class aircraft according to aircraft physical characteristics, aircraft noise and engine exhaust emissions. The calculation time of the simplified best practice model is only about 20% of that of the original model. Pretto et al. [43, 44] used Automatic Dependent Surveillance-Broad (ADS-B) data and web data as the input of the best practice model to draw the noise contour map of the area near airports in Europe. Experiments have proved the effectiveness of noise prediction and the feasibility of short-term noise prediction based on large-scale web data in the case of complex flight paths. The best practice models in the ECAC.CEAC Doc.29 (3rd Edition) [45, 46], the AzB model [47], the FAA's Integrated Noise Model (INM) [48] and Aviation Environmental Design Tool (AEDT) are constantly updated with the development of theory.

3.2 Scientific Model

The scientific model is mainly based on the acoustic principle, which usually includes the noise source model and noise propagation model. The model first considers noise from the component level of the aircraft, including propulsion system noise (jet engine noise, fan component noise, etc.) and fuselage structure noise (landing gear noise, flap noise, etc.) at least [6], and then use the noise propagation model to complete the prediction of noise. When using the scientific model, one or more groups of parameters need to be input to describe the physical characteristics of the noise source system. The accuracy of prediction depends on the quantity and quality of input parameters. There are three main ways to obtain these parameters: (1) Direct measurement under controllable conditions; (2) Obtaining from aircraft and engine manufacturers; (3) Generated using trusted simulation tools. However, the high measurement cost, the confidentiality of manufacturing and assembly data and the uncertainty of simulation all determine that a lot of later work is needed to evaluate and improve the quality of input data [39].

Therefore, the main characteristics of the scientific model are high complexity, difficulty in data acquisition and high cost, which determines that this model is not suitable for the prediction of the absolute noise level in complex airport scenes [49]. This kind of model is applicable to some scientific research scenarios, such as designing noise abatement procedures, predicting noise in aircraft or engine design and manufacturing stage. Unlike the best practice model, this kind of model is only applicable to a small number of specific aircraft. To explore the impact of aircraft speed and configuration on noise in approach and take-off procedures, Thomas et al. [50] proposed a fleet noise framework, which can predict the effective perceived noise level of engines and fuselages of six types of aircraft, and the prediction error is within − 2.2 to 3.7 dB. A year later, Thomas et al. [51] developed a framework including aircraft deceleration rate, fuselage component noise and engine noise, which can be used to evaluate the impact of delayed deceleration approach procedure on community noise. It is found that the delayed deceleration approach procedure can reduce the noise under the flight track by 4–8 dB (A) in the area far from the final approach stabilization point.

Scientific models are divided into two categories: semi-empirical model and full parameter model. Semi-empirical models include the multi-source model SIMUL [39] of DLR and the multi-source model sonAIR of Empa [52], etc. Full parameter models include the Panam model of DLR [49], the ANOPP 2 model of NASA [53], the Carmen model of ONERA [54], etc.

3.3 Machine Learning Model

The machine learning model takes historical noise data as the core, and comprehensively considers airport data, aircraft parameters, meteorological databases, geographic databases, etc. These models use machine learning methods to mine the implicit connections between data for the purpose of predicting future noise. Due to the implicit relationship between airport data, environmental parameters and other data and the availability of these data, the machine learning model is more accurate than the best practice model and more general than the scientific model. The disadvantage of the machine learning model is that, on the one hand, it is necessary to select appropriate mining algorithms according to different data conditions; on the other hand, as the so-called “Garbage in, Garbage out”, the quality of input data should be guaranteed before input, otherwise the prediction results will be unsatisfactory. The commonly used machine learning models include artificial neural network, linear regression, random forest, support vector machine and so on.

Figure 8 summarizes the general process of aviation noise prediction based on the machine learning model. The process can be divided into four steps: data preparation, model training, model validation and engineering application. First, the aircraft trajectory and other data are preprocessed and correlated with each other. In the model training stage, a training data set is developed for the training of the machine learning algorithm. At the same time, the test data set is constructed to evaluate the performance of the algorithm, and the hyperparameter set (the number of adjustable parameters, loss function, etc.) is adjusted and optimized through the algorithm evaluation. After selecting the appropriate model parameters, enter the model validation stage, use the prepared validation data set and model parameters to verify the machine learning model, and compare the measured noise data for final evaluation and adjustment. In the final engineering application stage. After determining the airport and aircraft, input the relevant data into the trained and validated noise prediction model to obtain the prediction noise data. Finally, post-processing and visualization are performed to obtain the specified output (contour map, specific noise metrics, etc.).

Fig. 8
figure 8

General flow chart of aviation noise prediction based on machine learning model

Full size image

The idea of artificial neural network comes from the structure of biological brain neurons. The artificial neural network is an intelligent model with learning ability, which has strong performance and is far superior to other machine learning algorithms in the fields of image recognition, text analysis, automatic driving and so on. However, its shortcomings are also very fatal. Compared with other machine learning algorithms, the neural network model has the disadvantages of long training time, large amount of data and high computing cost. One of the most famous shortcomings is the “black box” nature, that is, the process from input to output is difficult to understand in a trained neural network, and it is difficult to explain how and why the neural network obtains a certain output.

Vela and Oleyaei-Motlagh [55] developed a sequence-to-sequence modeling approach based on Long Short-Term Memory (LSTM) recurrent neural network for predicting aviation noise at ground locations. The model integrates relevant aircraft type data and weather data, and is based on more than 10 months of radar track data and noise history data. LSTM overcomes the shortcomings of gradient vanishing and gradient exploding in the ordinary recurrent neural network. The model can output the time series data of aircraft noise only by inputting the trajectory of the aircraft (without flap schedule and thrust of each point in the trajectory). In the output data, 73% of the predicted values are within 3 dB, and 90% of the predicted values are within 5 dB, showing excellent performance. If more data are integrated to expand the dimension of the LSTM model, the prediction will be more accurate. Based on the existing research on jet noise of jet aircraft, Tenney et al. [56] further studied and quantified the influence of feature space, learning rate and network structure on jet noise prediction results using deep neural network model. It is found that the deep neural network can accurately predict the far-field directional sound pressure level of jet noise, and the average error is within ± 0.75 dB. Considering the dynamic relationship between aircraft flight parameters and the corresponding 4D track, Revoredo et al. [57] developed a multilayer feedforward neural network to predict the aircraft noise level at the specified observation point. The model can be used to compare the noise impact of different arrival and departure procedures, and can evaluate the overall aircraft noise level at an observation point in the airport within a specified time period.

Regression analysis includes univariate/multivariate linear regression, binary/multiclass/ordered logistic regression, Partial least squares regression, etc. In aviation noise prediction, the most commonly used is multiple linear regression. Multiple linear regression is the generalization of univariate linear regression to multiple independent variables. The advantages of this method include the comprehensive consideration of multiple factors in the improved model, simple calculation, easy understanding, good identifiability, etc. However, it also has the following disadvantages: large prediction error, easy over fitting, unable to effectively solve the strong linear correlation between various regression variables, etc.

Based on the measured noise and flight parameters, Zellmann et al. [52] proposed a compromise scheme that takes into account the prediction accuracy and the amount of flight parameter data by using two multiple linear regression models for the fuselage and engine, respectively. They established aircraft noise emission models for 19 types of aircraft, reflecting the universality of their modeling methods for turbofan engine aircraft. Gagliardi et al. [58] predicted the noise level of monitoring points affected by a single take-off event by using principal component analysis and the multiple linear regression method. Experiments show that the actual take-off weight, ground speed and height of the aircraft relative to the observation point have the most significant interference effects on the noise level.

4 Aviation Noise Prediction Software

Many software born in the 1980s are undergoing updating and iteration in countries and regions with developed aviation technology. The growth history and technical characteristics of some representative software are sorted out below, and the access address is attached (Table 3).

Table 3 Main aviation noise simulation software
Full size table

4.1 Integrated Noise Model (INM)

Since 1978, the FAA's Office of Environment and Energy has jointly developed the Integrated Noise Model (INM) with ATAC Corporation and Volpe National Transportation Systems Center (VNTSC). The INM model is a best practice model. Based on the NPD database, the model uses the trajectory segmentation method to calculate the noise. For a long time, FAA has taken the INM as the standard tool for airport noise assessment. To make the INM meet the latest aircraft noise calculation standards, FAA continues to maintain and upgrade the model. In the mid-1980s, the INM model was written into computer software, and then FAA successively released several versions of the INM 5 series and the INM 6 series. In April 2007, INM was upgraded to version 7.0, which is also the last important series.

Compared with previous versions, version 7.0 is compatible with the methods contained in the latest ECAC.CEAC Doc.29 (3rd Edition) at that time, such as the new lateral attenuation adjustment algorithms and the updated flight path segmentation. Based on Heliport Noise Model (HNM) Version 2.2, INM version 7.0 also enhanced the ability to model helicopter noise [59]. Other important functions of the INM include but are not limited to, the assessment of aircraft noise impact around the airport, the assessment of noise impact changes caused by the newly constructed runway or runway expansion, and the assessment of noise impact changes caused by the new aircraft fleet configuration and new operational procedures. On the one hand, the acoustic and flight performance modeling of the INM 7.0 version has been enhanced. On the other hand, the introduction of many new functions, including the Scenario-Case Format, has greatly improved the usability and operational efficiency of the software [48].

Half a year after the release of INM 7.0, the INM 6 and 7 series have been used by more than 1000 organizations in 65 countries, and the number of users is increasing every year. The final version of the INM is INM 7.0d, released in September 2013. Since May 2015, the INM will not be updated. All its functions have been integrated into the Aviation Environmental Design Tool (AEDT).

Access address: https://www.faa.gov/about/office_org/headquarters_offices/apl/research/models/inm_model/.

4.2 Aviation Environmental Design Tool (AEDT)

AEDT 2a, released in March 2012, is the first version of AEDT. It should be noted that AEDT 2a is only used to replace the Noise Integrated Routing System (NIRS). The study area of AEDT 2a can contain multiple airports. This software is used to simulate the environmental consequences of the air traffic airspace and procedure actions 3000 feet above the ground that are being designed and implemented by the FAA’s Air Traffic Organization. AEDT 2b, released in May 2015, integrates the Integrated Noise Model (INM), Emissions and Dispersion Modeling System (EDMS) and AEDT 2a. Compared with the traditional tools mentioned above, AEDT 2b has a completely different system architecture and functions. It divides the flight path into more segments to enhance the correlation between flight path segments and aircraft status, so it can generate more accurate noise models. In terms of operational efficiency, AEDT 2b allows users to model aviation noise, fuel consumption and emissions at the same time [60]. Subsequently, FAA successively released 2c and 2d versions.

AEDT 3b was released in September 2019, which is an important version. The Base of Aircraft Data (BADA) Family 4 of the European Organisation for the Safety of Air Navigation (EUROCONTROL) began to be the key database for calculating aircraft performance. It enables AEDT 3b to provide improved modeling fidelity in the terminal area and calculate the noise and emissions from sophisticated flight procedures defined by users [61].

At present, the latest version of AEDT is 3e, which was released in May 2022. The highlights of AEDT 3e include the ability to import tracks and aircraft operations in CSV files, the ability to use U.S. Census 2020 data for population exposure reports, airport updates, fleet updates and study database updates, etc.

Using Geographic Information System (GIS) and relational database technology, AEDT 3e simulates aircraft operation from space and time dimensions to estimate the impact of aviation fuel consumption, emission, noise and aviation activities on air quality [62]. The software can generate customized reports on various factors of aircraft performance, which can be used not only for the modeling and analysis of a single flight at the airport but also for the application scenarios at the regional, national and global levels. FAA and U.S. Government use AEDT for aviation system planning, environmental policy analysis and other regulatory work.

Access address: https://aedt.faa.gov.

4.3 Aircraft NOise Prediction Program (ANOPP) and the Next-Generation Aircraft NOise Prediction Program (ANOPP 2)

NASA launched the Aircraft Noise Prediction Program (ANOPP) in the late 1970s. The original goal of ANOPP was to predict the community noise of turbofan-powered aircraft. Its theoretical manual was first published in February 1982. With continuous development, the community noise prediction module of propeller-powered aircraft has been added to ANOPP since June 1986 [63]. The prediction methodologies in ANOPP are empirical or semi-empirical models. Based on the best experimental data set available at that time, the performance of ANOPP in predicting the noise of conventional tube-and-wing aircraft is excellent, but the performance of ANOPP in predicting non-conventional hybrid wing body without measurement data is not satisfactory.

Considering the need for noise prediction of unconventional aircraft, the physics-based next-generation Aircraft NOise Prediction Program (ANOPP2) has been developed. ANOPP2 includes the methods in ANOPP, as well as a variety of propagation and noise prediction methods. The main capabilities of ANOPP2 include engine and airframe source noise prediction, calculation of the interaction between installations, noise propagation from around the aircraft to ground observers, and noise perceived by observers. The biggest advantage of ANOPP2 is that it provides a framework for combining multiple acoustic methods by using nested acoustic data surface technology, which allows users to use different fidelity methods simultaneously in a noise prediction [64].

The noise calculation process of ANOPP2 can be roughly divided into three stages. The first stage is to calculate the noise on the Source-Surface generated by each noise source on the aircraft. Then enter the next stage, that is, take the Source-Surfaces as the input to calculate the noise on the Mid-Surfaces around the entire aircraft. Each Source-Surface generates a penetrable Mid-Surface, namely FW-H surface [65], which is the highest fidelity data surface in ANOPP2. The Mid-Surfaces can be superimposed together while preserving the interaction between sound sources. In the final stage, the Far-Surface is in the observer's position. The noise transmitted from each Mid-Surface to the Far-Surface will be calculated and summed to obtain the final noise prediction result [66].

ANOPP2 can be used to evaluate the noise of aircraft components and aircraft systems, as well as aircraft noise reduction technology and flight procedures. With the ability to apply noise prediction to the new design, ANOPP2 can rapidly and reliably predict the noise of newly designed aircraft.

Access address: https://software.nasa.gov/software/LAR-18567-1.

4.4 FLULA2

Swiss Federal Laboratory for materials science and Technology (Empa) developed the aircraft noise calculation program FLULA2 in the late 1980s, which belongs to the best practice model. Because of the demand for calculation efficiency at that time, the noise source and noise propagation in FLULA2 are described by an empirical formula, which directly calculates and outputs the noise impact of the designated ground monitoring points. However, unlike the INM and AEDT, FLULA2 uses the time step method combined with the corresponding measured sound source database.

FLULA2 can use radar data or other three-dimensional fixed-point flight path of any shape to calculate aircraft noise. During the noise assessment, the position and speed of the aircraft are expressed in discrete time steps. The noise impact of the entire single flight event is obtained by solving the noise contribution of each point source with directional acoustic emission characteristics on the track to the monitoring point, and then the overall noise impact of multiple flights around the airport is obtained from multiple single events [67].

FLULA2 is one of the official aircraft noise calculation models in Switzerland. It is widely used in the aircraft noise calculation of Zurich Airport, Geneva Airport, military airfields, and other projects such as the Short and Long-Term Effects of Traffic Noise Exposure (SiRENE) research project.

Access address: https://www.empa.ch/web/s509/flula2.

4.5 sonAIR

Empa's acoustic/noise control laboratory has continued to develop the aviation noise assessment software sonAIR since 2012. The sonAIR seeks to overcome the limitations of best practices and scientific models, so it is designed to be flexible and can calculate aircraft noise with input parameters of different degrees of detail. Consequently, the sonAIR can not only accurately simulate the noise emission and propagation of a single flight but also apply to the noise assessment of the whole airport.

The sonAIR is composed of a semi-empirical sound source model and a sound propagation model. The sound source model uses a set of multiple regression models to describe the engine and airframe noise, respectively. The sound propagation model is further developed based on Empa's sophisticated sound propagation model sonX, taking into account atmospheric absorption, shielding effect, ground reflection, foliage attenuation and other factors [68]. Similar to FLULA2, the sonAIR can use the time step method to simulate a single flight event and reliably evaluate the noise at the monitoring points. It can also evaluate the long-term noise exposure around the airport by analyzing multiple flight events, output the noise map, calculate the number of people affected by noise. By combining the external noise database, the sonAIR can obtain the ability to evaluate the noise of the new aircraft design. In particular, if flight data recorder (FDR) data is available, which includes time and position information, Mach number, air density and N1 (rotational speed of the low-pressure compressor), sonAIR's performance will be better than FLULA2 and AEDT based on the best practice model [69].

Empa is currently working with the n-sphere company to integrate sonAIR with GIS. When the development is completed, sonAIR will replace FLULA2 as the official aircraft noise calculation model in Switzerland.

Access address: https://www.empa.ch/web/s509/sonair.

The access addresses of other noise prediction software are given below, which will not be introduced one by one.

5 Challenges and Prospects

Although the problem of aviation noise is becoming more and more serious, through the joint efforts of relevant stakeholders to improve metrics, optimize models and update software, we will eventually make considerable progress in the field of aviation noise research. The challenges and prospects are presented below.

  1. 1.

    The fundamental function of aviation noise evaluation metrics is to quantify aviation noise. The objective noise metrics with sound pressure, frequency, duration and other elements as the core have been relatively mature and widely used in the world. However, the impact of aviation noise on individuals is extremely subjective, which is affected by age, occupation, personality and other factors. The key subjective factors need to be determined through a lot of research and analysis, and then incorporated into the metric design. Such noise metrics will fully and accurately reflect the annoyance caused by aviation noise. In addition, the division of time period and the setting of penalty coefficient for some cumulative noise metrics should take into account the differences in social culture, economy, aviation technology level and other aspects in different regions. At the same time, flexibility and universality should also be considered when designing subjective metrics.

  2. 2.

    When predicting the overall noise level of the airport, the noise of each aircraft must be calculated. Relatively, when predicting the noise of a single aircraft, the noise generation mechanism needs to be analyzed in detail. Therefore, for a long time to come, the best practice model has irreplaceable advantages in evaluating the noise of complex air traffic scenes, while the scientific model will contribute more to “Reduction of Noise at Source”, which is one of the four balancing methods of ICAO. Scientific models will promote the development of best practice models by integrating the mechanisms for generating noise from related components.

    Data are the basis of the machine learning model. The quantity, dimension and quality of data determine the upper limit of prediction algorithm performance. Before building the machine learning model, it is necessary to determine the optimal monitoring point location layout using relevant layout optimization methods (such as spatial simulated annealing algorithm), measure a large amount of noise data, and expand the database dimensions by collecting radar trajectory, flight status, airport parameters, meteorological data and other data as much as possible. Finally, feature engineering methods (filtering, wrapping, embedding) are used to optimize the data set structure and quality. These preliminary preparations often require a lot of time and effort. In the process of building the model, we should also pay attention to the use of relevant optimization methods (such as genetic algorithm) to constantly adjust the model structure and hyperparameters so as to achieve the optimal prediction performance.

  3. 3.

    At present, the mainstream noise simulation software is based on best practice model and scientific model. With the rapid development of artificial intelligence (AI) technology, noise simulation software based on machine learning models has broad prospects.

    When data support is sufficient, it is necessary to consider how to speed up model training through parallel computing and other technologies under limited computing resources. Moreover, if we can integrate the Geographic Information System (GIS), number of people exposed, community annoyance and other factors into the software, and provide a noise contour map that can show the location distribution and subjective annoyance of people affected by aviation noise, such software will have irreplaceable advantages.

6 Conclusion

Focusing on the problem of aviation noise, this review analyzes and summarizes the literature on noise metrics, prediction methods and simulation software. The paper first puts forward the topic of aviation noise by introducing the future development trend of air transport and cities, and summarizes the hazards of aviation noise. Next, the article explains the changes in the use of common noise metrics in developed countries. According to the characteristics of metrics, they are divided into three categories: single event noise metrics, cumulative exposure metrics, and daily metrics. Based on the principle of aircraft noise prediction models, these models are divided into three categories: best practice models, scientific models, and machine learning models. The potential of machine learning models is pointed out. Then, the paper sorts out the useful simulation software in the study of aviation noise. Finally, challenges and prospects are put forward from different aspects. This review will give interested scholars a comprehensive understanding of aviation noise research.