From Bore–Soliton–Splash to a New Wave-to-Wire Wave-Energy Model

Abstract

We explore extreme nonlinear water-wave amplification in a contraction or, analogously, wave amplification in crossing seas. The latter case can lead to extreme or rogue-wave formation at sea. First, amplification of a solitary-water-wave compound running into a contraction is disseminated experimentally in a wave tank. Maximum amplification in our bore–soliton–splash observed is circa tenfold. Subsequently, we summarise some nonlinear and numerical modelling approaches, validated for amplifying, contracting waves. These amplification phenomena observed have led us to develop a novel wave-energy device with wave amplification in a contraction used to enhance wave-activated buoy motion and magnetically induced energy generation. An experimental proof-of-principle shows that our wave-energy device works. Most importantly, we develop a novel wave-to-wire mathematical model of the combined wave hydrodynamics, wave-activated buoy motion and electric power generation by magnetic induction, from first principles, satisfying one grand variational principle in its conservative limit. Wave and buoy dynamics are coupled via a Lagrange multiplier, which boundary value at the waterline is in a subtle way solved explicitly by imposing incompressibility in a weak sense. Dissipative features, such as electrical wire resistance and nonlinear LED loads, are added a posteriori. New is also the intricate and compatible finite-element space–time discretisation of the linearised dynamics, guaranteeing numerical stability and the correct energy transfer between the three subsystems. Preliminary simulations of our simplified and linearised wave-energy model are encouraging and involve a first study of the resonant behaviour and parameter dependence of the device.

1 Introduction

Early September 2010, three applied mathematicians at the University of Twente made requests to create a soliton in a make-shift wave tank for a new “research plaza” opening festivity. Part of that plaza contains a water feature or channel approximately $45\;\mathrm{m}$ long, $2\;\mathrm{m}$ wide, and $1.2\; \mathrm{m}$ deep. Normally filled to its edge with water and harbouring water plants and fish, at the time, it was only partially filled. A soliton is a wave with nonlinearity and dispersion in balance, such that the wave stays coherent and neither disperses nor breaks [13, 33]. Solitons or solitary waves can be generated at the beginning of a rectangular channel with vertical walls: using either a piston moving bespokely, a block lowered at a finite yet fast speed into the water or by a quick sluice-gate removal between a higher rest-water level ($h_1$) lock section and a lower rest-water level ($h_0$) main section. We have used the latter for solitary-wave generation with an extra channel feature, sketched in Fig. 1 with dimensions in Table 1: a V-shaped channel end with vertical walls.

While a soliton is a well-known mathematical and fluid-mechanical feature in nonlinear science, a general audience would be entertained more when such a travelling heap of water would lead to an extreme wave, to mark the plaza opening. We, therefore, added the V-shaped contraction to create the highest splash possible by only varying water levels $h_0$ and $h_1$ before and after the sluice gate, given a wave-channel geometry. Ideas for wave-height amplification arose from work on hydraulic flow stowage in contractions [2] and on wave impact against sea walls by Peregrine [6, 44], cf. Fig. 2. After some trials in two wave tanks, we created a “bore–soliton–splash”¹. The highest bore–soliton–splash—case 8 in Table 2—consists of time-dependent evolution summarised in Fig. 3: (a) water initially at rest with (b) an excavator ready to lift the sluice gate out of the channel; after sluice-gate removal, a coherent compound of “2.5” solitary waves travels towards the contraction and the highest solitary wave breaks shortly after its inception into (c) a so-called hydraulic bore or spilling breaker; the slightly lower non-breaking second wave is tailed by a lower third wave, with all three waves travelling at a slightly different speeds; during its propagation, the bore diminishes in height due to turbulent energy dissipation and (d) breaking ceases just before the contraction; the smoothened wave then amplifies and reflects in the V-shaped channel contraction and upon reflection draws a deep trough in which the second slightly lower wave crashes precisely, leading to (e, f) generation of a wave or splash circa ten times the incoming, first, and highest solitary-wave height. The bore–soliton–splash let to a variety of new ideas including its modelling and also the creation and testing of a proof-of-concept of an inspired wave-energy device. Our paper aims to highlight and partially investigate these ideas and to relate this splash or man-made rogue wave to similar rogue or monster waves in our oceans.

Fig. 1

Wave-channel set-up sketch with top and side views (left/right). Sluice-gate speed determined approximately by video analysis of the sluice-gate removal

Table 1 Details of soliton–splash experiment, including wave tank dimensions

Fig. 2

Wave impact against a wall in hydraulic facilities in Hannover, Germany. Photo courtesy: D. Howell Peregrine’s slide inherited by O.B. via the School of Mathematics, University of Bristol

Table 2 Table with all experimental trials to establish the highest bore–soliton–splash (BSS)

Rogue, monster, or extreme waves are anomalously high and rare waves with wave height $H_{{\text {rw}}}$, generally considered at sea, defined relative to a significant or ambient-wave height $H_{\text {s}}$ of surrounding, preceding, and following seas. A straightforward definition of rogue waves states that the abnormality index ${\text {AI}}=H_{{\text {rw}}}/H_{\text {s}}>2$, i.e., the rogue-wave height $H_{{\text {rw}}}$ must be at least twice as high as the ambient-wave height²$H_{\text {s}}$. Dysthe et al. [14] and Khariff et al. [31] provide more advanced and precise definitions of rogue waves, but this common definition given above suffices here. Rogue waves have a rare, extreme occurrence and are, therefore, difficult to predict, either statistically or deterministically. Understanding their wave height and occurrence is relevant to maritime and coastal engineering given their potential to damage ships, maritime, and coastal structures, including sinking and disappearance of ships; an overview of such disasters is found in Nikolkina and Didulenkova [41]. There are different types of rogue waves, involving linear and nonlinear wave focussing in one horizontal dimension, spatial wave focussing due to coastal or submarine convergences, episodic waves such as tsunamis generated elsewhere, and crossing seas with pyramidal waves [7, 16]. These different rogue-wave types have been (partially) explained within a hierarchy of different models, including, e.g., incompressible Euler equations with a free surface and passive or limited air motion, its potential-flow restriction, and numerous asymptotic approximations of these classical potential-flow water-wave equations such as Benney–Luke equations, Kadomtsev–Petviasvili’s (KP) equation, nonlinear Schrodinger equation(s), and the Korteweg–De-Vries equation [13, 28, 31, 40, 42, 43].

The main results achieved in this article are:

• a detailed description of a man-made bore–soliton–splash rogue wave with an abnormality index of ${\text {AI}}\approx 10$;

• establishing and employing mathematical and numerical models for experimental cases 8 and 9 (see Table 2), with improved simulations beyond the one in Bokhove and Kalogirou [4]; and,

• inspired by the bore–soliton–splash configuration, we invented a novel rogue-wave-energy device, and built and tested a scaled-down version; a first nonlinear mathematical model is developed here, for which we show simulations of its linearised dynamics.

Fig. 3

Time evolution snapshots of the highest bore–soliton–splash, case 8 in Table 2. a Channel overview before sluice gate is removed. b Sluice gate with excavator used to smoothly remove the sluice gate. After sluice-gate removal, c the highest solitary wave in the compound becomes a bore or spilling breaker, dissipating turbulent energy, and diminishing amplitude, while it propagates to become d smooth again before the contraction. After reflection, it draws a trough in which the second wave falls, thus forming e a jet f collapsing after reaching its apex

The outline of our paper is as follows. Soliton–splash and bore–soliton–splash experiments are analysed in Sect. 2. Some mathematical and numerical solutions of soliton splashes with Benney–Luke’s model are found in Sect. 3. In Sect. 4, our wave-energy device is introduced with one comprehensive and novel, nonlinear mathematical wave-to-wire model of the hydrodynamics, buoy motion, and power generation. After developing an intricate and novel compatible discretisation of that linearised model, numerical modelling results are presented. We finish with a discussion of open questions and challenges in Sect. 5, also highlighting a splash-inspired artwork.

2 Experimental Set-Up and Results

Our goal in 2010 was to create both a travelling soliton by removing a sluice gate separating two different water levels, initially at rest, and a splash of the highest possible amplitude in a V-shaped contraction. Given time constraints, the only way to determine whether our goal was reachable in practice was to resort to experimentation in two make-shift wave channels: the first one where the Roombeek, a brook, flows onto the University of Twente campus and the second one on the above-mentioned Research Plaza, see Fig. 3. On 20-09-2010, we managed to obtain two soliton splashes with $h_1\approx 2 h_0$ in the Roombeek convincing us that it was possible to make a larger and reproducible Plaza-channel soliton–splash. Subsequently, seven test cases were completed on 27-09-2010, including six with different rest-water levels $h_0$ and $h_1$, and one repeated case with the highest splash to ensure reproducibility on the opening day of the Research Plaza. The optimal case involved $h_0=0.41\pm 0.01\;\mathrm{m}$ and $h_1=0.9\pm 0.01\;\mathrm{m}$. These two repeat cases and the general outcomes on 27-09-2010 showed that our experiments to create a bore–soliton–splash were reproducible on the opening day (30-09-2010). All cases are summarised and dated in Table 2 with repeat cases underlined and numbered by 3, 6, and 8. On 30-09-2010, this “optimal” case was successfully repeated, as shown in Fig. 3, followed by a case numbered 9 with the higher water level of $h_0=0.43\;\mathrm{m}$ set in the main channel by the addition of sluice compartment’s extra water from optimal case 8, while keeping $h_1=0.9\;\mathrm{m}$; case 9 resulted in a smooth solitary-wave compound without wave breaking and a lower splash. Its evolution in time is displayed in Fig. 4 as bespoke simulations introduced and explained later. Videos of (nearly) all cases are found on Zweers’ YouTube channel [50] and numbered accordingly. Inspection of videos of three repeat cases 3, 6 and 8 reveals that there are some/minor differences, partially commented on in Table 2. We attribute differences to the estimated error of $\pm 0.01\;\mathrm{m}$ in initial water levels $h_{0,1}$ and the manner of sluice-gate removal by the excavator, despite training to be as consistent as possible. Case 9 underscores these sensitivities to the initial conditions, because a $0.02\;\mathrm{m}$ change from $h_0=0.41\;\mathrm{m}$ (cases 3, 6, and 8) to $0.43\;\mathrm{m}$, while keeping $h_1=0.9\;\mathrm{m}$, within measurement error, led to a quite different splash. Note, however, that the outcomes are not chaotic, as three reasonably repeatable cases demonstrate.

Several splash types were observed in the nine cases including minor/major reflections, resonances between waves (cases 3, 6, and 8), smooth waves, sheets (case 9), and pyramidal waves (cases 3, 6, and 8). Rogue-wave amplitudes found ranged between $H_{{\text {rw}}}\in [0.6,3.5]\pm {0.5}$ m, i.e., concerning errors in $H_{{\text {rw}}}$ of 14–$83\%$. For the highest cases of the bore–soliton–splash, we found $H_{\text {s}}=0.35\pm 0.05\;\mathrm{m}$ for the highest and first solitary wave and a rogue-wave height of $H_{{\text {rw}}}=[3.25,3.5,3.5]\pm 0.5$ m leading to a maximum abnormality index, cf. [10], in the range of:

$$\begin{aligned} AI = \frac{H_{{\text {rw}}}}{H_{\text {s}}} \in [{3}/{0.4},{3.5}/{0.3}] = [7.5,11.7]\approx 10, \end{aligned}$$

(1)

truly rogish compared to observations of a typical ${\text {AI}}\in [2,3]$ in the oceans. Coastal rogue waves can have a larger abnormality index, cf. [41] and the Tohoku Tsunami of 2011 [35] for which ${\text {AI}}\approx 5.25$. Finally, in November 2011, we created a portable bore–soliton–splash with also a circa tenfold amplification in a miniature wave channel of approximately $0.7\;\mathrm{m}$ long, $0.1\;\mathrm{m}$ in width and $0.065\;\mathrm{m}$ high, where we used $h_0=0.02\pm {0.001}\;\mathrm{m}$ and $h_1\approx 2 h_0$ to find $H_{{\text {rw}}}=0.2\;\mathrm{m}$. It again involved a solitary-wave compound of a highest solitary wave followed by a second and third one of lower amplitudes. Perhaps surprisingly, nonlinear and inertial effects still dominate over friction and also over surface tension. A mini-splash video of this table-top dissemination is found online [50].

Fig. 4

Numerical solution of soliton splash event case 9 with $\mu =0.04$ and $\epsilon =0.55$, see [4, 21]. When taking $h_0=0.43\ \mathrm{m}$ instead of $h_0=0.41\ \mathrm{m}$ as in case 8, with $h_1=0.9\ \mathrm{m}$ the same in both cases, no wave breaking occurs [5]. Photo times at $t=8,14,15,15 \pm 0.5\ \mathrm{s}$ (relative) of observations found in [4] can be compared with simulation times at $t = 8, 14, 15, 15.34\ \mathrm{s}$. Values displayed are in metres. The simulation involves $N_{\text {k}} = 8010$ elements of which $N_x N_y = 20\times 390 = 7800$ elements lie in the regular part of the channel and $N_x(N_x+1)/2 = 210$ elements in the triangular contraction. There are $N_n = 8431$ nodes with $(N_x+1)(N_y+1) = 8211$ nodes in the regular part of the channel and $N_x (N_x+2)/2 = 220$ nodes in the triangular contraction

3 Mathematical and Numerical Modelling of Soliton Splashes

The bore–soliton–splash involves a series of mathematical and fluid-mechanical ingredients: dispersion, nonlinearity, a turbulent spilling breaker, and collapsing splash. Assuming incompressible fluid flow with a free surface, dispersion in a solitary wave is balanced by nonlinearity due to advection, while the hydraulic bore or spilling breaker highlights that this balance is temporarily and locally broken till turbulent dissipation reduces wave amplitude sufficiently to restore that balance, as we saw in Fig. 3c, d. When the flow is in balance, the soliton compound and splash can be modelled with a single-valued free surface in a singly connected domain till the apex of the splash is reached. Both spilling breaker and collapse of the splash are seen to involve multiply connected domains with bubbles and droplets.

We will start our modelling of the bore–soliton–splash cases for a smooth single-valued free-surface and using potential-flow equations and approximations thereof. Approximations used include a Benney–Luke pair/system of equations. Alternatively, one can explore the single, unidirectional KP equation in two horizontal spatial dimensions. These approximations have the advantage that dispersion is anomalously high which prohibits wave breaking and is, therefore, robust with the disadvantage being that outcomes during wave breaking will be less realistic, as follows. Numerical solutions are required to solve potential-flow and Benney–Luke equations in the actual wave channel, while exact solutions are available for the KP equation in an idealised domain for idealised settings. We will use variational principles and asymptotic theory to enhance numerical stability and robustness: our (novel) numerical techniques are direct, compatible space–time discretisations of relevant variational principles.

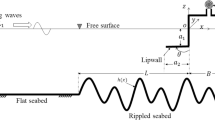
For potential-flow water waves, consider a free surface at $z=h(x,y,t)=H_0+\eta (x,y,t)$ over a flat bottom at $z=0$ with vertical coordinate z, and horizontal coordinates x and y as well as time t. Acceleration of gravity g acts in the negative z-direction. Water at rest sits at $z=H_0$ and $\eta =\eta (x,y,t)$ is the deviation from this rest level $H_0$. Three-dimensional velocity $\varvec{u}$ is approximated using a velocity potential $\phi =\phi (x,y,z,t)$ as $\varvec{u}=\varvec{\nabla }\phi$ with the gradient $\varvec{\nabla }=(\partial _x,\partial _y,\partial _z)^{\text {T}}$. The horizontal part of the domain $\varOmega _h$ is defined by a main channel of width $L_x$, with $x\in [0,L_x]$ and length $l_y(x)$, with $y\in [R(t),l_y(x)]$. The contraction is defined by $y=l_y(x)$ for $y\in [L_y-L_{\text {c}},L_y]$, where

$$\begin{aligned} l_y(x) = L_y - L_{\text {c}}|1 -2 x/{L_x}|, \end{aligned}$$

(2)

and the length of the contraction measured in the y-direction is $L_{\text {c}}$. The piston wavemaker R(t) will be used later, and for the solid wall at $y=0$ considered hitherto, we take $R(t)=0$. Our derivation starts from Luke’s [37] variational principle:

$$\begin{aligned} 0&= \delta \int _0^T\!\!\! \mathcal{L}_{\text {w}}[\phi ,\eta ]\,\mathrm{d}t \end{aligned}$$

(3a)

$$\begin{aligned}&= \delta \int _0^T\!\!\! \iint _{\varOmega _h}\int _{R(t)}^{H_0+\eta }\!\!\!\!\!\!\!\! \partial _t\phi +\frac{1}{2}|\varvec{\nabla }\phi |^2 + g (z-H_0-\eta _{\text {R}})\,{\mathrm d}z\, {\mathrm d}x\, {\mathrm d}y\,{\mathrm d}t, \end{aligned}$$

(3b)

modified to include a potential $\eta _{\text {R}}=\eta _{\text {R}}(x,t)$ modelling the removal of the sluice gate (cf. [4]) and with the horizontal domain extent $\varOmega _h$ of the wave channel. Collecting all variables into the vector of unknowns

$$\begin{aligned} \varvec{U} = (\phi ,\eta )^T, \end{aligned}$$

variations of (3) are defined as follows:

$$\begin{aligned}&\delta \int _0^T\mathcal{L}_{\text {w}}[\varvec{U}]\, {\mathrm d}{t} \equiv \lim _{\epsilon \rightarrow 0}\int _0^T \frac{\mathcal{L}_{\text {w}}[\varvec{U}+\epsilon \delta \varvec{U}]-\mathcal{L}_{\text {w}}[\varvec{U}]}{\epsilon }\,{\mathrm d}{t}. \end{aligned}$$

(4)

For $R(t)=0$, the potential-flow water-wave equations resulting from (3) read:

$$\begin{aligned} \varvec{\nabla }^2\phi&= 0\quad \text {in}\quad \varOmega _h, \end{aligned}$$

(5a)

$$\begin{aligned} \partial _z\phi&= 0\quad \text {at}\quad z=0, \end{aligned}$$

(5b)

$$\begin{aligned} \partial _t\eta +\varvec{\nabla }\phi \cdot \varvec{\nabla }\eta -\partial _z\phi&= 0\quad \text {at}\quad z=H_0+\eta , \end{aligned}$$

(5c)

$$\begin{aligned} \partial _t\phi +\frac{1}{2} |\varvec{\nabla }\phi |^2 +g(\eta -\eta _{\text {R}})&= 0\quad \text {at}\quad z=H_0+\eta , \end{aligned}$$

(5d)

$$\begin{aligned} \hat{\varvec{n}}\cdot \varvec{\nabla }\phi&= 0 \quad \text {on}\quad \partial \varOmega _h, \end{aligned}$$

(5e)

with $\hat{\varvec{n}}$ the unit normal vector and $\partial \varOmega _h$ the boundaries of the horizontal domain, i.e., any vertical walls—cf. the derivation in [37] with a minor change involving the sluice gate. To obtain the Benney–Luke system and a compatible/geometric finite-element discretisation on space and time, one can directly transform, discretise, and simplify (3b); for which details, we refer to [4, 21].

Simulations

The Benney–Luke equations have been used to simulate cases 8 and 9. The simulation of case 9 is seen to be surprisingly good from the visual comparison between the photographic images (cf. Fig. 11.5 in [4]) and snapshots of the simulation (see Fig. 4). The simulation of case 9 shown is an improvement of the simulation in [4], because we have used better meshing with a symmetric mesh before the contraction, as seen in Fig. 10. The simulation of case 8 does not compare well with the photographic images and video material. The primary reason is that simulations of cases 8 and 9 with the Benney–Luke equations are fairly similar, as the comparison between these cases along the centreline of the wave tank in Fig. 5 reveal. Consequently, the reduction of the wave amplitude and, hence, wave speed of the first soliton due to wave breaking in case 8 does not occur. The observed resonance between the first and second solitary waves in which the second wave exactly falls within the trough drawn by the reflection is, therefore, absent in the simulation of case 8. The wave dispersion in the Benney–Luke equations is too strong. Either a potential-flow type model with parametrised wave breaking is required or a model with the dynamics of a water–air mixture, including the localised wave breaking inherent in such a two-phase model.

Fig. 5

Snapshots at times $t=8.0,10.0,15.3\mathrm{s}$ of simulations for cases 8 (dashed lines) and 9 (solid lines), presented as profiles along the centreline of the wave tank, i.e., at $x=L_x/2=1\ \mathrm{m}$

4 Novel Rogue-Wave-Energy Device

We have created, designed, and tested a novel wave-energy device inspired by the bore–soliton–splash event. Our rogue-wave-energy device involves wave-activated buoy motion. It has elements, i.e., wave-focussing due to a tapered channel and a power take-off (PTO) mechanism for the electro-magnetic-induction generator, of three existing wave-energy devices [15]:

• The tapered channel or TapChan device; it consists of a tapered open channel which will enhance the wave amplitude, such that at the channel end the waves overtop a levy and water flows into a reservoir. Elsewhere along the reservoir, water flows down into a turbine to generate electricity via hydropower. A TapChan operated for a couple of years on a Norwegian island, bringing back electricity of $350\;\mathrm{kW}$ into the Norwegian grid, before it got damaged in a storm.

• The IPS wave buoy; it consists of a heaving buoy with a deep-lying piston moving into an anchored vertical shaft with a PTO mechanism to generate energy.

• The oscillating water column (OWC); it consists of a tapered channel in which the waves enter one open end of the channel, funnel, and amplify in an enclosed converging section that turns into a vertical blow hole at the top or the top side. Meanwhile, air compresses and decompresses by the rising and sinking wave leading to rapid air flow through the blow hole in which a wells’ turbine is situated and generates electrical power when air flows in either direction.

Fig. 6

Sketches of our wave-energy device with its horizontal axel at the contraction entrance, its three-dimensional buoy in the contraction indicated in yellow/orange, attached to an induction motor, consisting of magnets on the arc moving through the hollow cylindrical coils indicated in yellow, as well as a green and red LED (Color figure online)

Our device consists of a contracting channel with a wave buoy constrained to move in only one dimension, either in the vertical by sliding along a guiding mast or along a slightly curved arc pivoting around a horizontal axel at the contraction entrance. Attached to the buoy is either another vertical mast or a curved mast, to which magnets are attached that can move through a series of coils when the buoy is heaving due to the wave motion. An artistic rendering of the second version of the wave-energy device is given in Fig. 6. The latter magnet-and-coil system comprises a magnetic-induction motor, cf., the one in the Faraday shaking light shown in Fig. 7b. Relative to the version with the two vertical masts, one moving and one fixed, it has the advantage that the buoy can be taken out of action in storms and that a rotating axel is mechanically more robust than mast-guide ball bearings. Our device is intended to be part of a breakwater or dock, since waves will be absorbed.

In 2013, the “Berkeley wedge” wave-energy device was patented [38]. It is a wave-absorbing wedge moving on rails against a vertical wall attached to an induction motor. It is similar to our wave-energy device, but has no wave amplitude enhancing contraction like in the TapChan and OWC devices. During storms, the Berkeley wedge is sunk off into the water to protect it from damage. The Berkeley wedge operates in essence like a wavemaker reversed in time, following the principle that a good wave-energy device can also be good wavemaker, when time is reversed or energy is put in rather than being generated.

Fig. 7

Overview of the working proof-of-principle of our new wave-energy device, here powering one LED: a wave tank with wavemaker, powered by OB, and contraction; b two Faraday shaking lights, one entire, and one deconstructed with the magnets put onto the mast and the coils wrapped around a plastic tube; c the tube guiding the magnet with its surrounding coils and wires leading to the LED; and, d the unit of contraction, guiding mast, and buoy–mast unit, at rest

Before we advanced to any mathematical modelling, in the summer of 2013, we built and tested a proof-of-principle of our device to assess its viability. Our experimental set-up consisted of a straightforward wave tank with a hand-driven wavemaker, Fig. 7a, a shaped foam buoy with a mast topped by two magnets moving through a tube with four fixed coils, Fig. 7c, the latter parts coming out of two deconstructed shake or Faraday flashlights [22, 25, 39], Fig. 7b, with the buoy constrained to glide along a fixed, guiding mast. The shape of the buoy is close to a simplex with a slightly rounded and slanted bottom face and a flat-top face, Fig. 7d. To the induction motor, either one LED was connected to demonstrate the power output or an Arduinoscope (a hand-made oscilloscope using Arduino technology) to measure power output. Photographs of the set-up are given in Figs. 7 and 8. We powered one LED, but, given the AC-power generated, two (sets of) LEDs will be used in the mathematical model derived in the next section (see also [29, 30]). Two (sets of) LEDs, circuited in parallel yet operating for currents in opposite directions, harness twice the wave energy into light.³

Fig. 8

Details of our new wave-energy device: a the magnetic-induction motor consisting of the hollow tube with its four sets of coils; a tube through which the magnets on top of the buoy–mast move; and, b the blinking LED light (seen as the white flash at the top left), while the buoy is elevated by a wave to its top position

Fig. 9

a Sketch of a cross section at the centreline of the wave tank with a contraction at its right end, and b a top view with $L_y=2\;\mathrm{m}$, $L_x=0.2\;\mathrm{m}$ and $L_{\text {c}}=0.2508\;\mathrm{m}$

4.1 Wave-to-Wire Monolithic Wave-Energy Model

A comprehensive mathematical model of the new wave-energy device will be developed next within a domain constructed to reproduce an existing small-scale wave tank at the University of Leeds, which is a larger tank than the one used for the proof-of-principle. Both the wave-to-wire formulation of this wave-energy device is novel as well as the compatible and robust discretisation of the linearised model. Such a discretisation is important, because it guarantees numerical stability and the correct two-way feedback between pairs of the three subsystems. The numerical wave tank has a piston wavemaker on its left side, and consists of a channel with a flat bottom at $z=0$ that ends in a V-shaped contraction at the right end of the channel, cf. Fig. 9, as described in Sect. 3 and Eq. (2). A wave-energy buoy, here constrained to move only in the vertical, resides in the corner of the contraction. The shape of the buoy is described next.

The buoy is a simplex with a flat-top triangular face and has a slanted front face converging into one point at the bottom. The two remaining faces of the simplex align with the vertical walls of the V-shaped contraction. The slanted face is tilted to the vertical, as shown in the cross section at $x=L_x/2$ in Fig. 9a). The buoy motion can be described by its position $Z=Z(t)$ (note that given the constrained motion, this does not need to be the centre of gravity) and corresponding velocity $W=W(t)=\mathrm{d}Z/\mathrm{d}t$. Given this simplex geometry and assuming its flat-top face stays dry, the wetted buoy’s height above the flat bottom is located at

$$\begin{aligned} z= h_b\left( x,y;Z(t)\right) = Z(t) - {H}_k - \tan \alpha \,(y - L_y). \end{aligned}$$

(6)

Here, $\alpha$ is the angle between the hull bottom and the horizontal, $L_y$ is the maximum length along $x=L_x/2$ of the domain with the wavemaker at its rest position $y=0$, and ${H}_k>0$ is the vertical distance between the position Z(t) and the keel of the buoy (see Fig. 9a). The keel of this V-shaped buoy, therefore, lies at $(x,y,z)=(L_x/2,L_y,Z-H_k)$. The waterline point $y_{\text {b}}(x=L_x/2,t)$ at the centreline $x=L_x/2$ shown in Fig. 9 is defined as the point where the water meets the buoy. The overall waterline of the buoy is denoted by $y=y_{\text {b}}(x,t)$ and parameterised by x. At this waterline $y_{\text {b}}(x,t)$, for every x within the contraction, which x-interval varies over time, the height $h=h(x,y,t)$ of the free surface of the fluid equals the buoy’s surface height. That is $h\left( x,y_{\text {b}}^-(x,t),t\right) =h_{\text {b}}\left( x,y_{\text {b}}^+(x,t);Z(t)\right)$, with the appropriate limits indicated. Taking the variation of this expression, one finds that

$$\begin{aligned}&\delta h(x,y_{\text {b}}^-,t) = \delta h_{\text {b}}(x,y_{\text {b}}^+,t) \nonumber \\&\quad \Leftrightarrow \delta h|_{y_{\text {b}}^-} + \frac{\partial h}{\partial y}\big |_{y_{\text {b}}^-} \delta y_{\text {b}} = \delta h_{\text {b}}|_{y_{\text {b}}^+} + \frac{\partial h_{\text {b}}}{\partial y}\big |_{y_{\text {b}}^+} \delta y_{\text {b}} \nonumber \\&\quad \Leftrightarrow \quad \delta y_{\text {b}} = \frac{\delta Z - \delta h|_{y_{\text {b}}^-}}{\frac{\partial h}{\partial y}\big |_{y_{\text {b}}^-} + \tan \alpha }, \end{aligned}$$

(7)

which implies that $y_{\text {b}}$ is not an independent variable in the problem.

Table 3 Physical parameters used in three-dimensional numerical calculations for the wave buoy system, including wave tank dimensions, buoy’s mass, and physical properties of water at a room temperature of 25$\,^{\circ }\mathrm {C}$

The rest position of the buoy is directly determined geometrically via Archimedes’ principle given the mass M and rest position $\bar{Z}$ of the buoy, as follows. The angle $\theta _{\text {c}}$, defined by $\tan \theta _{\text {c}}=2 L_{\text {c}}/L_x$, with $\theta _{\text {c}}=68.26^{\circ }$ presently, is the angle between the opening of the contraction and the line across the contraction (as shown in the magnified right-hand-side panel in Fig. 9). A summary of the dimensions of the existing wave tank as well as other relevant physical parameters used in the numerical calculations can be found in Table 3. At rest, $y_{\text {b}}=L_{\text {b}}$ and given that $\tan \theta _{\text {c}}=2 L_{\text {c}}/L_x=(L_y-L_{\text {b}})/X_{\text {b}}$, the length of the waterline is $2 X_{\text {b}}=2(L_y-L_{\text {b}})/\tan \theta _{\text {c}}$, such that the submerged part of the buoy is a smaller simplex, isomorphic to the entire buoy simplex, defined by the following four points:

$$\begin{aligned} \mathbf{v}_0&= \left( \frac{1}{2}L_x,L_y,H_0\right) ^{\text {T}}, \quad \mathbf{v}_1 = \left( \frac{1}{2}L_x-X_{\text {b}},L_{\text {b}},H_0\right) ^{\text {T}}, \nonumber \\ \mathbf{v}_2&= \left( \frac{1}{2}L_x+X_{\text {b}},L_{\text {b}},H_0\right) ^{\text {T}}, \quad \mathbf{v}_3 = \left( \frac{1}{2}L_x,L_y,\bar{Z}-H_{\text {k}}\right) ^{\text {T}}. \end{aligned}$$

(8)

The volume $V_{\text {b}}$ of the submerged part of the buoy is then the displaced water mass divided by the density of water, i.e.,

$$\begin{aligned} V_{\text {b}} = \frac{M}{\rho _0}&= \frac{1}{6}|\det (\mathbf{v}_1-\mathbf{v}_0,\mathbf{v}_2-\mathbf{v}_0,\mathbf{v}_3-\mathbf{v}_0)| = \frac{1}{3}\frac{(H_0+H_{\text {k}}-\bar{Z})^3}{\tan \theta _{\text {c}}\tan ^2\alpha }, \end{aligned}$$

(9)

given that $\tan \alpha =(H_0+H_{\text {k}}-\bar{Z})/(L_y-L_{\text {b}})$ [calculated via (6) for $(x,z)=(L_y,H_0)$]. Consequently, for this three-dimensional tetrahedral buoy, the rest position of the buoy’s centre of mass is thus found to be:

$$\begin{aligned} \bar{Z}=H_0+H_{\text {k}} - \root 3 \of {\frac{3 M \tan \theta _{\text {c}} \tan ^2\alpha }{\rho _0}}, \quad \text {and} \quad L_{\text {b}}=L_y-\root 3 \of {\frac{3 M \tan \theta _{\text {c}}}{\rho _0\tan \alpha }}. \end{aligned}$$

(10)

Attached to the buoy is a vertical mast with two magnets on top, moving through a set of coils, whose constrained and vertical movement by induction comprises the actuator. Magnet and mast are all included in the overall weight M of the buoy. The current $I=I(t)$ is the derivative of the electrical charge $Q=Q(t)$, i.e., $I=\dot{Q}$. The coils have an overall inductance of $L_i$. Rather than using the current I(t), we use the conjugate momentum $P_{Q}= P_{Q}(t)$ as primary variable, defined in Appendix A by $P_{Q}= L_i\dot{Q}-K(Z)$ with

$$\begin{aligned} K(Z)&= \int ^Z \gamma G(\hat{Z})\mathrm{d}\hat{Z}, \end{aligned}$$

(11)

$\gamma = 2\pi a^2 \mu N/L$, magnetic dipole momentum $\mu$ of the magnet, a the radius of the coils, N the number of coil windings per metre, and L the length of the coils as well as a function G(Z) defined in (44f). This function G(Z) depends on the length of the mast $H_m$, the length $L_m$, and radius of the cylindrical magnet and the placement of the coils at $z\in [\bar{Z}+(1+\alpha _h) H_m-\frac{L}{2},\bar{Z}+(1+\alpha _h) H_m+\frac{L}{2}]$ with $0<\alpha _h<1$. A novel model of the magnetic-induction actuator is developed in Appendix A from first principles, using the Maxwell’s equations in a thin-wire approximation and given the cylindrical symmetry of the induction coils.

Hence, we can now formulate a comprehensive, or monolithic, variational principle of the entire, coupled water-wave problem, wave-activated buoy motion, and magnetic-induction actuator, as follows:

$$\begin{aligned} 0&=\delta \int _0^T\mathcal{L}[D,\phi ,h,\phi _{\text {s}},Z,W,Q,P_{Q},p,\lambda ] {\mathrm d}{t}\nonumber \\&\equiv \delta \int _0^T \rho _0 \int _{0}^{L_x} \int _{R(t)}^{l_y(x)}\int _0^{h(x,y,t)}\!\!\!\!\!\!\!\! D\partial _t \phi \,{{\,\mathrm{d}\,}}\!z{{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x -M W\dot{Z}-P_{Q}\dot{Q}+\mathcal{H}\,{\mathrm d}{t} \end{aligned}$$

(12a)

$$\begin{aligned}&\equiv \delta \int _0^T \rho _0 \int _{0}^{L_x} \int _{R(t)}^{l_y(x)}\int _0^{h(x,y,t)}\!\!\!\!\! D\partial _t \phi +\frac{1}{2} {D}|\varvec{\nabla }\phi |^2+ g D\left( z-H_0\right) \nonumber \\&\qquad \qquad + p(D-1)\, {{\,\mathrm{d}\,}}\!z{{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x\nonumber \\&\qquad \qquad + \underline{\rho _0 \int _{0}^{L_x} \int _{R(t)}^{l_y(x)} \lambda (h-h_b)\varTheta \left( y-y_b(x,t)\right) \, {{\,\mathrm{d}\,}}\!x{{\,\mathrm{d}\,}}\!y}\nonumber \\&\qquad \qquad -{M}W\dot{Z}-P_{Q}\dot{Q}+\frac{1}{2} M W^2+ M g Z+\frac{1}{2} \frac{\bigl (P_{Q}+K(Z)\bigr )^2}{L_i}\,{{\,\mathrm{d}\,}}\!t, \end{aligned}$$

(12b)

with $\phi _s=\phi (x,y,h(x,y,t),t)$ the velocity potential evaluated at the free surface, $\varvec{\nabla }$ the three-dimensional gradient, and $\mathcal{H}$ the Hamiltonian. Herein, a scaled pressure $p=p(x,y,z,t)$ acts as Lagrange multiplier to impose the incompressibility constraint $D-1=0$ of a scaled density $D=D(x,y,z,t)$, such that the density $\rho (x,y,z,t)=\rho _0 D(x,y,z,t)$, cf. [9]. Moreover, the single-valued free water surface at $z=h(x,y,t)$ with water depth $h=h(x,y,t)$ is constrained [underlined terms in (12)] to be the dynamic shape of the wave-buoy using the Lagrange multiplier $\lambda (x,y,t)$ over the wetted part $y>y_{\text {b}}(x,t)$ of the wave-buoy hull—see also [30]. We have used the Heaviside function $\varTheta (y-y_{\text {b}})$, zero for $y<y_{\text {b}}$ and unity for $y\ge y_{\text {b}}$, to single out this wetted part of the hull. The key reason to include the scaled density D and impose incompressibility condition $D-1=0$ weakly is that variational principle (12) mathematically yields the boundary condition on $\lambda$ at the waterline, as a consistency component of the entire formulation. This condition follows from the system of equations emerging next. In contrast, when one imposes the constraint $D=1$ strongly, the (interface) condition for $\lambda$ at the waterline needs to be imposed a priori.

As before, we collect all variables into the vector of unknowns

$$\begin{aligned} \varvec{U} = (D,\phi ,h,\phi _s,Z,W,Q,P_{Q},p,\lambda )^T, \end{aligned}$$

with variations of (12) defined as in (4). Most variations of (12) emerge in a straightforward manner; only the variations involving the terms $D\partial _t\delta \phi$, $D\varvec{\nabla }\phi \cdot \varvec{\nabla }(\delta \phi )$, and a comprehensive term involving the variations of the free surface $\delta h$ in the upper integration limit are more complicated and require integration by parts in time and the use of Gauss’ law—see [9, 18] for more details. Given these hints, while leaving further derivation details to the reader, variation of (12) yields the following, fully nonlinear, equations of motion:

$$\begin{aligned} \delta D:\;&\partial _t\phi +\frac{1}{2}|\varvec{\nabla }\phi |^2+g(z-H_0)+p=0, \end{aligned}$$

(13a)

$$\begin{aligned} \delta \phi :\;&\partial _t D+\varvec{\nabla }\cdot (D\varvec{\nabla }\phi ) = 0, \end{aligned}$$

(13b)

$$\begin{aligned} \delta p:\;&D=1, \end{aligned}$$

(13c)

$$\begin{aligned} \delta \lambda : \quad&h-h_{\text {b}} = 0\quad \text {for}\quad y\ge y_{\text {b}}(x,t), \end{aligned}$$

(13d)

$$\begin{aligned} \delta \phi _{\text {s}}:\;&\partial _th +\varvec{\nabla }\phi \cdot \varvec{\nabla }h = \partial _z\phi \quad \text {at}\quad z=h(x,y,t), \end{aligned}$$

(13e)

$$\begin{aligned} \delta h:\;&\partial _t\phi +\frac{1}{2}|\varvec{\nabla }\phi |^2+g(h-H_0)+\lambda \varTheta \left( y-y_b(x,y,t)\right) =0 \nonumber \\&\qquad \qquad \qquad \text {at}\quad z=h(x,y,t), \end{aligned}$$

(13f)

$$\begin{aligned} \delta \phi _R:\;&\dot{R} = \partial _y\phi \quad \text {at}\quad y=R(t), \end{aligned}$$

(13g)

$$\begin{aligned} \delta W:\;&\dot{Z} = W, \end{aligned}$$

(13h)

$$\begin{aligned} \delta Z:\;&M \dot{W} +M g + \frac{\gamma G(Z)}{L_i}\bigl (P_{Q}+K(Z)\bigr )\nonumber \\&\qquad \qquad -\rho _0 \int _{0}^{L_x} \int _{R(t)}^{l_y(x)} \lambda \varTheta \left( y-y_b(x,t)\right) \, {{\,\mathrm{d}\,}}\!x{{\,\mathrm{d}\,}}\!y= 0, \end{aligned}$$

(13i)

$$\begin{aligned} \delta P_{Q}:\;&\dot{Q} = \frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}\equiv I, \end{aligned}$$

(13j)

$$\begin{aligned} \delta Q:\quad&\dot{P}_Q = 0, \end{aligned}$$

(13k)

with $\phi _R=\phi (R(t),y,z,t)$ the velocity potential evaluated at the wavemaker. Evaluation of (13a) at the free surface $z=h$ and subtraction of (13f) yields that

$$\begin{aligned} p = 0\quad \text {for}\quad y < y_{\text {b}}(x,t),\quad \text {and}\quad p = \lambda \quad \text {for}\quad y \ge y_{\text {b}}(x,t), \end{aligned}$$

(14)

such that $y=y_{\text {b}}(x,t)$ at the waterline on the wave-buoy, from which it necessarily follows that $\lambda \left( x,y_{\text {b}}(x,t),t\right) =0$.

A straightforward way to model the energy harvesting is the use of two (sets of) LED diodes in parallel but positioned in opposite directions, such that only one (set of) LED(s) is active at one time. Using the Shockley equation, as model for the LED–voltage–current relationship for current flow in either direction, yields that the voltage

$$\begin{aligned} V_{\text {s}}(I) = -\mathrm{sign}(I) n_{\text {q}} V_{\text {T}} \ln {\left( {|I|}/{I_{{\text {sat}}}}+1\right) } \end{aligned}$$

(15)

is really a function of $I=I(t)$; the $\mathrm{sign}$-function and absolute value |I| used ensure operation and damping for currents in either direction. Since such an LED model leads to damping, it is less common to include it a priori in the variational principle and damping/loading is added a posteriori to the model by substitution of (15) for $V_{\text {s}}(t)$. Parameters in the Shockley model for LEDs include the saturation current $I_{{\text {sat}}}$, the quality factor $n_{\text {q}}$, and the thermal voltage $V_{\text {T}}$. In addition, we added resistance terms $-(R_{\text {c}}+R_i)I$, with a resistance $R_i$ of the wiring to the LEDs as well as a resistance $R_{\text {c}}$ of the coils, in the equation for $P_{Q}$, to model losses for the circuit and LED diodes combined. Instead of $\dot{P_{Q}}=0$ in (13), one then obtains

$$\begin{aligned} \dot{P}_Q = -(R_{\text {c}}+R_i)I -\mathrm{sign}(I) n_{\text {q}} V_{\text {T}} \ln {\left( \frac{|I|}{I_{{\text {sat}}}}+1\right) }~\text {with}~ I = \frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}.\quad \end{aligned}$$

(16)

The total electrical power output P is then the time integral $P=\int _0^T I(t) V_{\text {s}}(t)\, \mathrm{d}t$, with $V_{\text {s}}(t)$ the voltage across the LEDs.

In the rest state, we saw that the straight waterline lies at $y=L_{\text {b}}$ with rest depth $H(x,y)=H_0$ for $y<L_{\text {b}}$, while for $y\ge L_{\text {b}}$, a rest depth H(x, y) as well as (rest-state) Lagrange multiplier $\varLambda (x,y)$ are defined by:

$$\begin{aligned} H(x,y)&= \bar{Z} - H_{\text {k}}-\tan \alpha (y-L_y), \nonumber \\ \varLambda (x,y)&= g\left( H_0+H_{\text {k}}-\bar{Z}+\tan \alpha (y-L_y)\right) , \end{aligned}$$

(17)

with the rest position $\bar{Z}$ of the buoy. Hence

$$\begin{aligned} \frac{\partial {\varLambda }}{\partial {y}} = g\tan \alpha . \end{aligned}$$

(18)

To linearise the equations of motion (13), we consider the following decomposition of variables into rest-state and (small-amplitude) perturbations:

$$\begin{aligned} \phi (x,y,z,t)&=\tilde{\phi }(x,y,z,t),\quad D(x,y,z,t)=1+\tilde{D}(x,y,z,t),\nonumber \\ h(x,y,t)&= H(x,y)+\eta (x,y,t),\quad p(x,y,z,t)= g(H_0-z)+\tilde{p}(x,y,z,t),\quad \nonumber \\ \lambda (x,y,t)&=\varLambda (x,y)+\tilde{\lambda }(x,y,t),\quad y_{\text {b}}(x,t) = L_{\text {b}}+\tilde{y}_{\text {b}}(x,t),\nonumber \\ Z(t)&= \bar{Z}+\tilde{Z}(t),\quad W(t)= \tilde{W}(t),\nonumber \\ Q(t)&=\tilde{Q}(t),\quad P_{Q}(t)=-K(\bar{Z})+{\tilde{P}_{Q}}(t), \end{aligned}$$

(19)

the latter relation taken, such that the rest current $\bar{I}=0$, since $P_{Q}=L_i I - K(Z)$. Upon linearising, the moving domain becomes a fixed domain $y\in [0,l_y(x)]$ with a fixed waterline at $y=L_{\text {b}}$. After a Taylor expansion, the waterline condition for $\tilde{\lambda }$ at $y=L_{\text {b}}$ becomes:

$$\begin{aligned} 0 = \lambda (x,y_{\text {b}},t) \approx \frac{\partial {\varLambda (x,y)}}{\partial {y}}\biggr |_{y=L_{\text {b}}}\tilde{y}_{\text {b}} + \tilde{\lambda }(x,L_b,t), \end{aligned}$$

(20)

where we used that $\varLambda (x,L_{\text {b}})=0$ by definition and omitted quadratic and higher order terms in the perturbation variables. Expansion of the waterline condition (7) leads to an explicit expression for $\tilde{y}_{\text {b}}(x,t)$ in terms of $\tilde{Z}(t)$ and the free surface at the linearised waterline $\eta (x,L_{\text {b}}^{-},t)$; to wit

$$\begin{aligned} \tilde{y}_{\text {b}}(x,t)&= \frac{\left( \tilde{Z}(t)-\eta (x,L_{\text {b}}^{-},t)\right) }{\tan \alpha }. \end{aligned}$$

(21)

By combining (20) and (21), we obtain the desired boundary condition at the linearised waterline, that is

$$\begin{aligned} \tilde{\lambda }(x,L_{\text {b}},t) = g\left( \eta (x,L_{\text {b}}^{-},t)-\tilde{Z}(t)\right) . \end{aligned}$$

(22)

It means that $\tilde{\lambda }(x,L_{\text {b}},t)$ is not an independent variable at $y=L_{\text {b}}$. We highlight that the derivation of this subtle (weak) condition (22) on $\tilde{\lambda }$ has only been possible, because we deferred the strong imposition of the incompressibility condition $D=1$ or $\tilde{D}=0$.

The final simplifications are that we consider the system in both the linear and shallow-water limits, yielding that the velocity potential $\tilde{\phi }=\tilde{\phi }(x,y,t)$ is a function of only the horizontal coordinates and time, now with $\varvec{\nabla }=(\partial _x,\partial _y)^{\text {T}}$. The equations of motion and induction in these linear, shallow-water limits become:

$$\begin{aligned}&\eta -\tilde{Z} = 0\quad \text {for}\quad y\ge L_{\text {b}}, \quad \dot{R} = \partial _y\tilde{\phi }\quad \text {at}\quad y=0, \end{aligned}$$

(23a)

$$\begin{aligned}&\partial _t\eta + \varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi })= 0, \end{aligned}$$

(23b)

$$\begin{aligned}&\partial _t\tilde{\phi } +g\eta +\tilde{\lambda }\varTheta (y-L_{\text {b}})=0, \end{aligned}$$

(23c)

$$\begin{aligned}&\dot{\tilde{Z}} = \tilde{W}, \end{aligned}$$

(23d)

$$\begin{aligned}&M \dot{\tilde{W}} +\gamma G(\bar{Z})\frac{\left( {\tilde{P}_{Q}} +\gamma G(\bar{Z})\tilde{Z}\right) }{L_i}-\rho _0 \int _{0}^{L_x} \int _{0}^{l_y(x)}\!\!\!\tilde{\lambda }\varTheta (y-L_{\text {b}})\, {{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x= 0, \end{aligned}$$

(23e)

$$\begin{aligned}&\dot{\tilde{Q}} = \frac{\left( {\tilde{P}_{Q}}+\gamma G(\bar{Z})\tilde{Z}\right) }{L_i}, \end{aligned}$$

(23f)

$$\begin{aligned}&{\dot{\tilde{P}}_{Q}} = -\bigl (R_{\text {c}}+{R_i}+\frac{n_{\text {q}} V_{\text {T}}}{I_{{\text {sat}}}}\bigr ) \frac{\left( {\tilde{P}_{Q}}+\gamma G(\bar{Z})\tilde{Z}\right) }{L_i}, \end{aligned}$$

(23g)

$$\begin{aligned}&\varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\lambda })-\frac{\rho _0}{M}\int _{0}^{L_x}\!\!\!\int _{0}^{l_y(x)}\!\!\!\!\tilde{\lambda }\varTheta (y-L_{\text {b}})\, {{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x= -\varvec{\nabla }\cdot (g H\varvec{\nabla }\eta )-\frac{\gamma }{M}G\left( \bar{Z}\right) \tilde{I}\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \text {for}\qquad y\ge L_{\text {b}}, \end{aligned}$$

(23h)

where we have added the effective circuit and coil resistances $R_i$ and $R_{\text {c}}$ and linearised (around $I=0$ and using $\bar{Z}$) model of the LED light, as well as a consistency equation, with (22) and $\hat{\varvec{n}}\cdot \varvec{\nabla }\tilde{\phi }=0$ at the fixed, vertical walls. Note that from (23f), $\tilde{I}=({\tilde{P}_{Q}}+\gamma G(\bar{Z})\tilde{Z})/L_i$. When we rework (23g) and take $\dot{\tilde{I}}$ to be negligible, then the linearisation is seen to lead to a damping term proportional to $\dot{\tilde{Z}}=\tilde{W}$ in the momentum equation, cf. [11, 12]. In addition, the linearisation of the LED model (16) is seen to lead to an effective resistance $n_{\text {q}} V_{\text {T}}/I_{{\text {sat}}}$, with linearised LED voltage $\tilde{V}_{\text {s}}(\tilde{I})=n_{\text {q}} V_{\text {T}}/I_{{\text {sat}}}\tilde{I}$. The (linearised) electrical power output $\tilde{P}(t)$ is calculated as a function of time and is given by $\tilde{P}=(\tilde{V}_{\text {s}}+\tilde{V}_{\text {r}})\tilde{I}$, with $\tilde{V}_{\text {r}}=(R_{\text {c}}+R_i)\tilde{I}$ the lost voltage due to circuit resistance.

A consistency equation arises by taking the time derivative of the primary constraint $\eta -\tilde{Z}=0$, which leads to a secondary constraint, given by

$$\begin{aligned} \varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi })+\tilde{W}=0, \end{aligned}$$

(24)

upon using two of the equations of motion to eliminate time derivatives. Subsequently taking the time derivative of this secondary constraint (24), while using two other equations of motion to eliminate the emerging time derivatives, yields the elliptic equation (23h) for $\tilde{\lambda }$.

4.2 Time Discretisation of the Linearised System

The time discretisation of the eight main equations in (23), i.e., in a count excluding boundary conditions, needs to be such that a time discretisation of the first seven equations is equivalent to, and consistent with, a time discretisation of the last seven equations, given that there are seven unknowns. The chosen time discretisation is a symplectic Euler one [19, 34], given the conjugate pairs of variables $\{\tilde{\phi },\eta \},\{\tilde{W},\tilde{Z}\},\{{\tilde{P}_{Q}},\tilde{Q}\}$. Hence, the time-discrete system with discrete time levels $t^n$ and $t^{n+1}=t^n+\varDelta t$ reads:

$$\begin{aligned}&\eta ^{n+1}-\tilde{Z}^{n+1} = 0\quad \text {for}\quad y\ge L_{\text {b}}, \end{aligned}$$

(25a)

$$\begin{aligned}&\frac{(\tilde{\phi }^{n+1}-\tilde{\phi }^{n})}{\varDelta t} +g\eta ^n +\tilde{\lambda }^n\varTheta (y-L_{\text {b}})=0,\ \end{aligned}$$

(25b)

$$\begin{aligned}&\frac{(\tilde{W}^{n+1}-\tilde{W}^n)}{\varDelta t} + C_1 G(\bar{Z}) {(\tilde{P}_{Q}^n+\gamma G(\bar{Z})\tilde{Z}^n)} \nonumber \\&\qquad \qquad - C \int _{0}^{L_x} \int _{0}^{l_y(x)}\tilde{\lambda }^n\varTheta (y-L_{\text {b}})\, {{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x= 0, \end{aligned}$$

(25c)

$$\begin{aligned}&\frac{({\tilde{P}_{Q}}^{n+1}-{\tilde{P}_{Q}}^n)}{\varDelta t} = - C_2 {({\tilde{P}_{Q}}^{n+1}+\gamma G(\bar{Z})\tilde{Z}^n)}, \end{aligned}$$

(25d)

$$\begin{aligned}&\frac{(\tilde{Z}^{n+1}-\tilde{Z}^n)}{\varDelta t} = \tilde{W}^{n+1}, \end{aligned}$$

(25e)

$$\begin{aligned}&\frac{(\tilde{Q}^{n+1}-\tilde{Q}^n)}{\varDelta t} = \frac{({\tilde{P}_{Q}}^{n+1}+\gamma G(\bar{Z})\tilde{Z}^n)}{L_i}, \end{aligned}$$

(25f)

$$\begin{aligned}&\frac{(\eta ^{n+1}-\eta ^n)}{\varDelta t} + \varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi }^{n+1})= 0\nonumber \\&\qquad \text {with}\quad \partial _y\tilde{\phi }^{n+1}|_{y=l_y(x)}=0,\qquad \partial _y\tilde{\phi }^{n+1}|_{y=0} = \dot{R}^{n+1}, \end{aligned}$$

(25g)

$$\begin{aligned}&\varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\lambda }^n)-C\int _{0}^{L_x}\!\!\!\int _{0}^{l_y(x)}\tilde{\lambda }^n\varTheta (y-L_{\text {b}})\, {{\,\mathrm{d}\,}}\!y{{\,\mathrm{d}\,}}\!x= -g \varvec{\nabla }\cdot (H\varvec{\nabla }\eta ^n)\nonumber \\&\qquad \qquad - C_1 G(\bar{Z}){(\tilde{P}_{Q}^n+\gamma G(\bar{Z})\tilde{Z}^n)} \quad y\ge L_{\text {b}}\nonumber \\&\qquad ~\text {with}~ \tilde{\lambda }^n(x,L_{\text {b}},t) = g\left( \eta ^n(x,L_{\text {b}}^{-},t)-\tilde{Z}^n(t)\right) ~\text {and}~ \hat{\varvec{n}}\cdot \varvec{\nabla }\tilde{\lambda }^n|_{\partial \varOmega _h,y>L_y-L_{\text {b}}}=0, \end{aligned}$$

(25h)

$C=\rho _0/M$, $C_1=\gamma /(M L_i)$, and $C_2=({R}_{\text {c}}+R_i+{n_{\text {q}} V_{\text {T}}}/I_{{\text {sat}}})/L_i$. By subtracting the $\tilde{Z}$-equation from the $\eta$-equation, we obtain:

$$\begin{aligned} \frac{(\eta ^{n+1}-\tilde{Z}^{n+1})}{\varDelta t} = \frac{(\eta ^n-\tilde{Z}^n)}{\varDelta t} -\tilde{W}^{n+1}- \varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi }^{n+1}). \end{aligned}$$

(26)

Given that $\eta ^n-\tilde{Z}^n=0$ and $\tilde{W}^{n}+\varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi }^{n}) = 0$, both imposed at time level $n=0$ initially, ensuring that $\eta ^{n+1}-\tilde{Z}^{n+1}=0$ implies that we have to show that

$$\begin{aligned} \tilde{W}^{n+1}+\varvec{\nabla }\cdot (H\varvec{\nabla }\tilde{\phi }^{n+1}) = 0. \end{aligned}$$

(27)

Using the equation for $\tilde{W}^{n+1}$ and operating $\varvec{\nabla }\cdot \left( H(x)(\cdot )\right)$ on Eq. (25b) for $\tilde{\phi }^{n+1}$, the consistency condition is seen to be (25h). Hence, (25) is consistent.

4.3 Space Finite-Element Discretisation of the Linearised System

The model (23) is discretised in a few steps. The first step is to multiply the field equations in (23) by $C^0$–test functions, and then integrate over space and by parts. The second step is to expand the fields using (special) $C^0$-continuous and compact finite-element basis functions. We will use standard linear and compact Galerkin basis and test functions, which are unity at their home node and zero at neighbouring nodes of the elements connected to the home node. The result is a space-discrete system which will be revealed to be only consistent for certain special choices of the function spaces and expansions. Vice versa, we can first discretise time in a consistent manner, such that again the equations remain consistent as we showed already. Finally, by either discretising the space-discrete system properly in time or the proper time-discrete system in space, we obtain an internally consistent overall space–time discretisation fit for numerical implementation.

The mesh is assembled using uniform quadrilateral elements up to the entrance of the contraction, with $N_x$ elements in the x-direction and $N_y$ elements in the y-direction, i.e., in the uniform section of the domain, the mesh comprises $N_xN_y$ elements and $(N_x+1)(N_y+1)$ nodes. In the contraction, the chosen mesh is still formed by quadrilateral elements, but now nodes are only aligned in every other line. A sample mesh is shown in Fig. 10. The tessellation of the contraction region increases the total number of elements by $N_x(N_x+1)/2$ and the number of nodes by $N_x(N_x+2)/2$. It is thus clear that the way the mesh is constructed provides a restriction in the choice of $N_x$, which needs to be even. The total number of elements is $N_{el}=N_x N_y+N_x(N_x+1)/2$ and the total number of nodes is $N_n=(N_x+1)(N_y+1)+N_x(N_x+2)/2$. The rest-state waterline is such that it is aligned with one of the nodal lines parallel to the x-direction.

Fig. 10

Computational mesh for $N_x=10$, $N_y=15$. The mesh structure in the contraction can be seen in the magnified right-hand-side plot, where the nodes in the contraction are denoted with a red $\times$ symbol. While our finite-element model can deal with unstructured meshes, our partially structured meshes tend to be faster and more accurate (Color figure online)

The nodes in the entire mesh are denoted by $k,l=1,2,\dots ,N_n$ and the $N_{n}-N_p+1$ nodes under the buoy are in the ordered case denoted by $\tilde{k},\tilde{l}=N_p,\dots ,N_{n}$. The latter include the nodes on the waterline, which in the current linearised case lies on the line $y=L_{\text {b}}$; the $N_{\text {b}}$ nodes on the waterline are a subset thereof, in the ordered case denoted by $\tilde{b}=N_p,\dots ,N_p+N_b-1$. When the $N_b$ nodes on the waterline are excluded in the latter, we use index $\hat{k}$. We multiply both wave equations (23b)–(23c) by the $C^0$-test function $\varphi _{k}(x,y)$ and the elliptic equation (23h) as well as the constraint (23a) by $\varphi _{\tilde{k}}(x,y)$ to obtain the weak forms after integration by parts, upon using the Neumann/Dirichlet conditions at $y=0$, $x=0,L_x$ for $y\in [0,L_y-L_{\text {c}}]$ and $y=l_y(x)$ for $x \in [0,L_x]$ and $y\in [L_y-L_{\text {c}},L_y]$. Also, $\lambda _h(x,y,t)=\lambda _{\hat{k}}(t)\varphi _{\hat{k}}(x,y)+\lambda _{\tilde{b}}(t)\hat{\varphi }_{\tilde{b}}(x,y)$, with $\hat{\varphi }_{\tilde{b}}$ being the part of the test function $\varphi _{\tilde{b}}\ge L_b$ under the buoy and $\lambda _{\tilde{b}}=g(\eta _{\tilde{b}}-\tilde{Z})$. Unfortunately, the consistency required cannot be shown for this choice of test function $\hat{\varphi }_{\tilde{b}}$ at the waterline. We, therefore, made some adjustments: we take $\lambda _h(x,y,t)=\lambda _{\tilde{k}}(t)\varphi _{\tilde{k}}(x,y)$ to be the normal test function spanning across the waterline with $\tilde{k},\tilde{l}=N_p,\dots ,N_{n}$ and thus smooth out the Heaviside function to allow inclusion of the full basis function $\varphi _{\tilde{b}}$ at the waterline $y=L_b$. Hence, the Heaviside function $\varTheta (y-L_b)$ is removed. This changes de facto only the vector and matrix definitions of $\tilde{S}_{\tilde{k}\tilde{l}}$, $\tilde{Q}_{\tilde{b}}$ and $N_{k \tilde{b}}$ below. The corresponding finite-element discretisation then becomes

$$\begin{aligned} N^T_{\hat{k}l}\left( \eta _{{l}}-1_{l}\tilde{Z}\right)&= 0, \end{aligned}$$

(28a)

$$\begin{aligned} M_{kl} \dot{\phi }_l&= -g M_{kl}\eta _l-N_{k\hat{l}} \lambda _{\hat{l}}- N_{k \tilde{b}}\lambda _{\tilde{b}}, \end{aligned}$$

(28b)

$$\begin{aligned} M_{kl} \dot{\eta }_l&= S_{kl}\phi _l+T_k \dot{R}, \end{aligned}$$

(28c)

$$\begin{aligned} \dot{\tilde{Z}}&= \tilde{W}, \end{aligned}$$

(28d)

$$\begin{aligned} \dot{\tilde{W}}&= C\tilde{Q}_{\hat{l}}\lambda _{\hat{l}}+C\tilde{Q}_{\tilde{b}}\lambda _{\tilde{b}}- C_1 G(\bar{Z}) {(\tilde{P}_{Q}+\gamma G(\bar{Z})\tilde{Z})}, \end{aligned}$$

(28e)

$$\begin{aligned} \dot{\tilde{Q}}&= \frac{({\tilde{P}_{Q}}+\gamma G(\bar{Z})\tilde{Z})}{L_i}, \end{aligned}$$

(28f)

$$\begin{aligned} \dot{\tilde{P}}_{Q}&= - C_2 {({\tilde{P}_{Q}}+\gamma G(\bar{Z})\tilde{Z})}, \end{aligned}$$

(28g)

$$\begin{aligned} \left( \tilde{S}_{\hat{k}\hat{l}} + C \tilde{Q}_{\hat{k}}\tilde{Q}_{\hat{l}}\right) {\lambda }_{\hat{l}}&= -g S_{\hat{k}l}\eta _{l}-C \tilde{Q}_{\hat{k}}\tilde{Q}_{\tilde{b}}\lambda _{\tilde{b}}-\tilde{S}_{\hat{k}\tilde{b}}\lambda _{\tilde{b}} \nonumber \\&\qquad \qquad + C_1 \tilde{Q}_{\hat{k}}G(\bar{Z})({\tilde{P}_{Q}+\gamma G(\bar{Z})\tilde{Z}}), \end{aligned}$$

(28h)

with several mass and “Laplace” matrices defined by:

$$\begin{aligned} M_{kl}&= \int _{0}^{L_x}\int _0^{l_y(x)}\varphi _k(x,y)\varphi _l(x,y)\,\mathrm{d}x\,\mathrm{d}y, \end{aligned}$$

(29a)

$$\begin{aligned} S_{kl}&= \int _{0}^{L_x}\int _0^{l_y(x)} H(y)\varvec{\nabla }\varphi _k(x,y)\cdot \varvec{\nabla }\varphi _l(x,y)\,\mathrm{d}x\,\mathrm{d}y, \end{aligned}$$

(29b)

$$\begin{aligned} \tilde{S}_{\hat{k}\hat{l}}&= \int _{0}^{L_x}\int _0^{l_y(x)}H(y) \varvec{\nabla }\varphi _{\hat{k}}(x,y)\cdot \varvec{\nabla }\varphi _{\hat{l}}(x,y)\,\mathrm{d}x\,\mathrm{d}y, \end{aligned}$$

(29c)

$$\begin{aligned} \tilde{Q}_{\hat{k}}&= \int _{0}^{L_x}\int _0^{l_y(x)}\varphi _{\hat{k}}(x,y) \,\mathrm{d}x\,\mathrm{d}y, \end{aligned}$$

(29d)

$$\begin{aligned} N_{k\hat{l}}&= \int _{0}^{L_x}\int _0^{l_y(x)} \varphi _k(x,y)\varphi _{\hat{l}}(x,y)\,\mathrm{d} x\,\mathrm{d}y, \end{aligned}$$

(29e)

$$\begin{aligned} T_k&= \int _{0}^{L_x} H(x,0) \varphi _k(x,0)\,\mathrm{d}x. \end{aligned}$$

(29f)

Nonzero contributions only exist for the tilded matrices and vectors for certain index ranges.

The key consistency check is to ensure that the first seven equations in (28) are consistent with the last seven equations in (28). Consider the first seven equations. Take the time derivative of the primary constraint and eliminate the time derivatives using two of the other seven equations, to obtain the secondary constraint:

$$\begin{aligned} N_{\hat{k}l}^T\left( M^{-1}_{lk} (S_{km}\phi _m+T_k \dot{R}) - 1_l \tilde{W} \right)&= 0. \end{aligned}$$

(30)

Now, take the time derivative of this secondary constraint above and again eliminate the time derivatives using two different equations of these seven equations, to obtain the consistency equation

$$\begin{aligned}&\left( N^T_{\hat{k}l}M^{-1}_{lk}S_{km}M^{-1}_{mn}N_{n\hat{l}}+C N^T_{\hat{k}l} 1_l \tilde{Q}_{\hat{l}}\right) \lambda _{\hat{l}} = -g N^T_{\hat{k}l}M^{-1}_{lk}S_{km} \eta _m\nonumber \\&\qquad \qquad -\left( N^T_{\hat{k}l}M^{-1}_{lk}S_{km}M^{-1}_{mn}N_{n\tilde{b}}+C N^T_{\hat{k}l} 1_l \tilde{Q}_{\tilde{b}}\right) \lambda _{\tilde{b}}\nonumber \\&\qquad \qquad + N^T_{\hat{k}l}M^{-1}_{lk}T_k\ddot{R}+ C_1 N^T_{\hat{k}l} 1_l G(\bar{Z})\left( \tilde{P}_{Q}+\gamma G(\bar{Z})\tilde{Z})\right) . \end{aligned}$$

(31a)

This consistency equation matches the last equation (28h) if and only if the following relations hold:

$$\begin{aligned} \tilde{S}_{\hat{k}\hat{l}}&= N^T_{\hat{k}l}M^{-1}_{lk}S_{km}M^{-1}_{mn}N_{n\hat{l}} \end{aligned}$$

(31b)

$$\begin{aligned} S_{\hat{k}m}&= N^T_{\hat{k}l}M^{-1}_{lk}S_{km} \end{aligned}$$

(31c)

$$\begin{aligned} \tilde{S}_{\hat{k}\tilde{b}}&= N^T_{\hat{k}l}M^{-1}_{lk}S_{km}M^{-1}_{mn}N_{n\tilde{b}} \end{aligned}$$

(31d)

$$\begin{aligned} \tilde{Q}_{\hat{k}}&= N^T_{\hat{k}l} 1_l \end{aligned}$$

(31e)

$$\begin{aligned} N^T_{\hat{k}l} M_{lk}^{-1} T_k&= 0. \end{aligned}$$

(31f)

These relations have been verified to hold up to machine precision. To date, we have not been able to verify these relations analytically. Finally, we find the consistent space–time discretisation by logically combining the time-discrete and space-discrete approaches derived in (25) and (28).

4.4 Numerical Results

We have set up a numerical code which simulates the full system as it evolves in time, including the generation/propagation of waves, their impact on the wave-energy buoy, the response of the buoy, and the power output. The numerical results presented next have been obtained using a mesh resolution of $N_x=10$ and $N_y=50$, i.e., the total number of elements in the calculations is $N_{{\text {el}}}=555$ and the total number of nodes is $N_n=621$. The time step used is $\varDelta t=0.0028\;\mathrm{s}$. At the start of the simulation the system is at rest and the water depth in the main wave tank is $H_0=0.1\;\mathrm{m}$. For $t>0$, waves are generated from the left wall of the tank by a piston wavemaker that follows a periodic motion in time according to $R(t)=\tfrac{A}{\omega }(1-\cos (\omega t))$, with amplitude $A=0.0653\;\mathrm{m}$ and frequency $\omega =\frac{6\pi }{L_y}\sqrt{gH_0}=9.3348\;\mathrm{s}^{-1}$ (which corresponds to a physical frequency of $\omega /2\pi =1.4857\;\mathrm{Hz}$). Therefore, on the left wall, $\partial _y\tilde{\phi }=\dot{R}(t)=A\sin (\omega t)$.

The total energy of the system E(t) is computed numerically as a function of time. The respective energies of the water $E_{\text {w}}$ (kinetic and potential), the buoy $E_{\text {b}}$, and the electro-magnetic system $E_i$ are defined by (the continuum forms are given below):

$$\begin{aligned} E_{\text {w}}&= \int _0^{L_x}\int _0^{l_y(x)} \left( \frac{1}{2}\rho _0H|\varvec{\nabla }_{}\tilde{\phi }|^2 + \frac{1}{2}\rho _0g\eta ^2 \right) \,{\mathrm d}y\,{\mathrm d}x, \end{aligned}$$

(32a)

$$\begin{aligned} E_{\text {b}}&= \frac{1}{2}M\tilde{W}^2, \qquad E_i = \frac{1}{2}L_i\tilde{I}^2. \end{aligned}$$

(32b)

Applying appropriate manipulations of equations in (23), by integrating in space the respective equations valid within the fluid and adding all of the resulting expressions, results in an equation for the time derivative of the total energy in time. This is not expected to be zero as in conserved systems but negative, due to the added damping in the system. In particular, we find:

$$\begin{aligned} \frac{{\mathrm d}E}{{\mathrm d}t} = -\tilde{P}, \end{aligned}$$

(33a)

with $E=E_{\text {w}}+E_{\text {b}}+E_i$ the total energy and $\tilde{P}=\tilde{P}_{\text {l}}+\tilde{P}_{\text {g}}$ the loss, separated into the resistive dissipation $\tilde{P}_l$ as well as the power gained $\tilde{P}_g$ via the LEDs, defined by:

$$\begin{aligned} \tilde{P}_{\text {l}}(t)&= \tilde{I}(t)\tilde{V}_{\text {r}}(t)=(R_{\text {c}}+R_i)\tilde{I}^2(t), \end{aligned}$$

(33b)

$$\begin{aligned} \tilde{P}_{\text {g}}(t)&= \tilde{I}(t)\tilde{V}_{\text {s}}(t)=n_{\text {q}}V_{\text {T}}/I_{{\text {sat}}}\tilde{I}^2(t). \end{aligned}$$

(33c)

Fig. 11

Vertical displacement of the buoy $\tilde{Z}(t)$ in meters m (top panel), current $\tilde{I}(t)$ in amperes A (middle panel), and total power $\tilde{P}(t)$ in watts or volt times ampere $\mathrm{V}\cdot \mathrm{A}$ (bottom panel) generated by the LEDs (blue) or lost in the circuit (orange) (Color figure online)

Fig. 12

Snapshots from the simulation in a wave tank with V-shaped contraction and a wave-energy buoy in the corner of the contraction. The surface shown is the numerically computed wave height $h(x,y,t)=H(x,y)+\eta (x,y,t)$ (in metres $\mathrm{m}$) with $H_0=0.1\;\mathrm{m}$

The results of a simulation with the parameters described earlier can be seen in Figs. 11 and 12. The response of the buoy is shown in the top panel of Fig. 11, while the electrical current is shown in the middle panel and the power generated in the bottom panel. Both the power generate ($\tilde{P}_{\text {g}}(t)$ blue line) and the resistive loss ($\tilde{P}_{\text {l}}(t)$ orange line) are displayed. Two snapshots of the computed wave height and buoy position in the contraction are displayed in Fig. 12.

In what follows, we consider a smoothed-out motion of the piston wavemaker which only attains its maximum amplitude A (as described in the first paragraph of this section) after two periods of oscillation. The wavemaker motion comprises two signals $R_1(t)$ and $R_2(t)$, which are out-of-phase initially, become in-phase after the first two oscillations, and then return back to be out-of-phase after N oscillations. The wavemaker hence stops operating after N oscillations at $t=T_{\text {w}}=2\pi N/\omega$ and the simulation continues until $T=2T_{\text {w}}$. Consequently N wave packets are sent into the wave tank. The motion of the wavemaker (and the respective signals $R_1$, $R_2$) can be seen in Fig. 13, and the resulting wave deviation from the still water level $H_0=0.1\;\mathrm{m}$ at the left wall is shown in Fig. 14.

Fig. 13

The motion of the piston wavemaker in time, defined by the composition of two signals. The second signal is constructed to have a time-dependent phase difference from the first signal, so that the wavemaker reaches its maximum amplitude smoothly, and returns to the stationary position in a similar manner. The wavemaker operates for $0\le t\le T_{\text {w}}$, with $T_{\text {w}}=6.7309\;\mathrm{s}$, and the simulation runs until $T=2T_{\text {w}}=13.4618\;\mathrm{s}$

Fig. 14

Deviation from the still water level at the wavemaker of the wave tank (at $x=0$, $y=0$) as a function of time. Since the waves are generated by a piston wavemaker, the deviation is uniform along the wall $y=0$. The wavemaker operates for $0\le t\le T_w$, with $T_w=6.7309\mathrm{s}$

Before performing any further simulations, we tested the accuracy of the numerical scheme both in time and space. The convergence of the Symplectic Euler method for the time-integration results is investigated by plotting the energy signal E(t) for two time steps $\varDelta t$ and $\varDelta t/2$ (Fig. 15). The bounded oscillations in the energy signal (shown in Fig. 15 only after the wavemaker stops adding energy in the system, i.e., for $t\ge T_{\text {w}}$), are seen to be approximately reduced by $41\%$ when computed with the half time step indicative of an accuracy of $\sim (\varDelta t)^{3/4}$. We note that the energy calculation using half the spatial resolution gives an accuracy of $\sqrt{\varDelta t}$, which suggests that the desired convergence of $\varDelta t$ may be achieved, albeit slowly, for a sufficiently resolved mesh. The spatial convergence rate evaluated using the formula, cf. [47]:

$$\begin{aligned} n = \frac{1}{\log 2}\log \left( \frac{\Vert \tilde{\phi }_1-\tilde{\phi }_3\Vert }{\Vert \tilde{\phi }_2-\tilde{\phi }_3\Vert }\right) , \end{aligned}$$

(34)

where the norm is taken to be either the $\mathcal {L}_1$, $\mathcal {L}_2$ or $\mathcal {L}_\infty$ norm. The subscripts 1, 2, and 3 correspond to the different mesh sizes in Table 4, obtained by halving the mesh spacing uniformly in each direction, or equivalently by doubling the number of elements. The convergence of the spatial discretisation, while expected to be of order 2, is seen to be circa 1.7.

Fig. 15

Energy signal E(t) for $T_{\text {w}}\le t\le T$, computed using a time step $\varDelta t=0.0014$ and the half time step $\varDelta t/2=0.0007$. The mesh resolutions used are $N_x=20$, $N_y=100$

Fig. 16

Total power output for varied a load coefficient $C_{\text {s}}=n_{\text {q}}V_{\text {T}}$ as used in the Shockley equation (15), b coil winding number N (while fixing $R_i$ using the values from Table 5 including the N-value stated), c buoy mass M, or d wavemaker frequency $\omega$. The notation [.] refers to a time-average over the total time of each simulation, i.e., $[\tilde{P}]=\frac{1}{T}\int _0^T \tilde{P}(t)\,{\mathrm d}t$

Table 4 Convergence rates n using three different norms ($\mathcal {L}_1$, $\mathcal {L}_2$, $\mathcal {L}_\infty$) evaluated using the value of the velocity potential $\tilde{\phi }$ at the final time of the simulation, i.e., at $t=T$. The time step used is such that the CFL condition is satisfied in similar fashion for each mesh resolution

We next investigate the influence of various system parameters such as the induction coils, buoy mass, and wavemaker frequency on the amount of power generated (and used to illuminate the LEDs) or lost due to circuit resistance. Figure 16 shows how the mean of the power $[\tilde{P}]$, defined by the time-average $[\tilde{P}]=\frac{1}{T}\int _0^T \tilde{P}(t)\,{\mathrm d}t$, where T is the final simulation time, changes for varying Shockley equation coefficient $C_{\text {s}}=n_{\text {q}}V_{\text {T}}$ [see Eq. (15)], coil winding number N, buoy mass M, and wavemaker frequency $\omega$. Panel (a) shows that the total power generated increases linearly with $C_{\text {s}}$, while the power lost decreases and is seen to asymptote for larger values of $C_s$. We find that for larger values of $C_{\text {s}}$, the current $\tilde{I}$ remains unaffected as a consequence of the fact that the wave state in the tank and the buoy response do not change with $C_{\text {s}}$. The linear dependence of $[\tilde{P}_{\text {g}}]$ on $C_{\text {s}}$ is due to the linearisation of the model. Furthermore, the increased power generation seen in panel (b) for smaller values of N is anticipated as it corresponds to lower resistance and inductance in the system (recall the definitions of $R_{\text {c}}$ and $L_i$—see Table 5—which are both proportional to parameter N). The curves in panel (b) are both seen to be proportional to $1/N^2$; hence, taking even lower values or N (or equivalently a shorter coil) yields a much higher production of energy. The variation of the power with the mass of the buoy is seen to be minimal (panel c), but follows a monotonic increase. Higher values of M were not considered here to avoid having a very low centre of gravity relevant to the still water level. Different buoy, contraction, and wave tank geometries/sizes (and hence buoy masses) will be considered in future work. Finally, it is observed that an optimal power generation can be achieved at certain wavemaker frequency, in this particular case at $\omega =10.89\;\mathrm{s}^{-1}$ (see also [3] for related results for the dependence on wavemaker amplitude and frequency for a slightly different set-up). This critical value appears to be the resonant frequency of the system considered. The energy of the system around this optimal frequency is illustrated in the top panel of Fig. 17, shown for times $T_{\text {w}}\le t\le T$ with $T_{\text {w}}=6.7309\;\mathrm{s}$ and $T=2T_{\text {w}}$. The respective energies of the subsystems (water, buoy, and electro-magnetic system) are also shown in the bottom panels of Fig. 17. Clearly, the total energy shown in the top panel remains approximately constant (the small oscillations observed remain bounded in time), while the energy lost from the water around $t=7\;\mathrm{s}$ and $t=11.5\;\mathrm{s}$ is converted into kinetic energy of the buoy and electrical energy in the inductor, even though the latter is much smaller in this case. One way to improve the efficiency of the wave-energy converter is by adding more LEDs in serial and/or reducing the length of the induction coils (cf., Fig. 16a, b).

Table 5 Indicative parameter values and units used in three-dimensional numerical calculations for the wave–buoy system. LED: https://en.wikipedia.org/wiki/Shockley_diode_equation

Fig. 17

Numerically computed energy (difference) of the full system (top panel) and respective energies of water (bottom left), wave-energy buoy (bottom middle), and electro-magnetic system (bottom right). The overbar notation denotes the difference between total energy and the energy when the wavemaker no longer moves, i.e., at $T_{\text {w}}=5.77\;\mathrm{s}$. Here, the “optimal” wavemaker frequency $\omega =10.89\;\mathrm{s}^{-1}$ is used

5 Summary and Discussion

In summary, we have reported in detail on the creation of the bore–soliton–splash, summarised modelling of this hydrodynamic splash, and showed how it inspired a novel wave-energy device. We will next provide further context of our work.

Relation to rogue waves at sea The bore–soliton–splash is a nonlinear wave-resonance phenomenon in which a series of travelling solitons reflect in a V-shaped contraction leading to a tenfold resonant amplification of the initial main wave height. Once created in 2010, the phenomenon caught attention of the rogue-wave community. Rogue waves are extreme and rare waves, generally but not exclusively sea waves, at least twice as high as the wave height of the ambient sea. While the original bore–soliton–splash was engineered, it relates to several rogue-wave phenomena at sea, far from and near the coastline. Rogue waves can have several causes and emerge in different situations: rogue-wave emergence in crossing seas, either due to seas with two main directions, e.g., high seas generated by two hurricanes, or one hurricane changing direction. More rare are seas with waves and swell from three different main directions. Our V-shaped contraction walls can, therefore, be re-interpreted as virtual walls concerning two (virtual) waves travelling under two angles $\pm \varphi$ from the main wave’s direction with two (virtual) planes of no-normal flow leading to a converging point. One difference is that the virtual case supports wave propagation with one splash at one space–time point, cf. [20], while our engineered set-up with solid walls necessarily leads to reflections.

Further modelling of the bore–soliton–splash and related rogue waves We reported (bore–)soliton–splashes including one with smooth solitary waves in which nonlinearity and dispersion are balanced without any wave breaking. The smooth soliton–splash of case 9 was successfully simulated using a compatible, geometric finite-element discretisation of a Benney–Luke model, a bidirectional simplification of the classic potential-flow model for water waves. Case 8 for the maximum bore–soliton–splash was not simulated correctly by the Benney–Luke model. Due to the lack of wave breaking, the case 8 simulation deviated significantly from reality in that the observed resonant interaction was absent. On one hand, it is possible to further explore simplified modelling of rogue waves in crossing seas using the Kadomtsev–Petviashvili (KP) equation, cf. [1, 20, 21, 28, 32]. On the other hand, more advanced modelling of the bore–soliton–splash will either require a full potential-flow model with localised and parameterised wave breaking or the use of models with actual, localised wave breaking while maintaining good dispersion properties. Single-phase or two-phase mixture-theory models, including ones with a Van-der-Waals-type equation of state, may also be good candidates [23, 46].

Alternatively, we have explored use of Smoothed Particle Hydrodynamics (SPH)⁴; such a numerical method [24] can handle wave breaking and jet collapse into bubbles and droplets, and can be used to simulate the bore–soliton–splash of case 8. SPH lies at the other end of the spectrum of numerical techniques, compared to the geometric numerical techniques used by us. To date, SPH does, however, turn out to be too dissipative. It requires too many degrees of freedom and thus too much computational power to avoid detrimental numerical wave-amplitude dissipation. Consequently, dispersive wave propagation over longer distances remains relatively poor in SPH. In our attempts, to date, the splash amplitude simulated by SPH was too low, even though we had replaced wave propagation in the channel prior to the contraction by several laterally periodic slices, copies of one another, to significantly reduce computational resources, before waves in these slices were fed into the contraction.

Fig. 18

The steel–soliton–splash is an artistic rendering in stainless steel of two snapshots of the bore–soliton–splash of case 8 [48, 49]

Optimisation of the wave-energy device Our splash inspired the creation of a novel wave-energy device and we showed a working, experimental proof-of-principle model, but also developed and derived a new and fully nonlinear mathematical model of the combined water-wave dynamics, the wave-activated buoy, and the magnetic-induction power generator. Essential ingredients of this comprehensive model have been captured in one variational principle to which we a posteriori added dissipative effects of the electrical circuit, coils of the actuator, and LEDs used as the loads. The overall model was subsequently linearised and discretised using a finite-element method in space and time. This (linear) algebraic model was made fully compatible with the variational structure in the conservative and continuum limits. Its compatible, novel, and nontrivial discretisation was augmented with the resistances of the electrical circuit and coils of the induction motor as well as the LED loads. Preliminary simulations of the linear model showed promising results including (suboptimal) convergence and energy transfer between the three components. Finally, we investigated the resonant behaviour of the system as function of wave-frequency and load for a long wave-packet of harmonic waves. Nonlinear modelling, optimisation, and control of the wave-energy device require further exploration, and both the geometry of contraction, mass, and wave-buoy shape could be optimised for a given wave climate. We also aim to explore feedback control as function of contraction geometry, the number of coils of the induction motor, and the total load. In addition, higher order and more accurate spatial and temporal discretisation schemes require exploring.

Steel–soliton–splash artwork We finish on an artistic note. Our bore–soliton–splash inspired an artwork, the steel–soliton–splash [49], created by WZ. Snapshots of the video of case 8 were first outlined as silhouettes, two of which formed the basis for a three-dimensional artwork, scaled down by about a factor of three, and welded in stainless steel, see Fig. 18. In 2013, we donated the artwork to the Isaac Newton Institute of Mathematical Sciences in Cambridge, UK.

Appendix: Model of Induction Generator

The induction motor modelled consists of a series of permanent cylindrical magnets attached to the top of the wave-buoy’s vertical mast. These magnets move through a series of coils connected in a circuit to two (sets of) LEDs, the loads, placed in two parallel directions, with half of the LEDs placed in one direction and the other half in the other direction. The latter placement guarantees that always one (set of) LED(s) is lighting up under the alternating current. The first modelling step is to calculate the magnetic flux $\mathbf{B}$ induced in the series of coils. The second modelling step is to calculate the voltage and current across and through the coils using Ohm’s law for the current density, electrical field, and magnetic flux. This moving magnetic flux $\mathbf{B}$ induces a current $I=I(t)$ in the coils. The third modelling step is to calculate the magnetic force and, via Newton’s law, the force on the buoy–mast–magnet system.⁵

First step The magnetic flux of a magnet, a cylinder magnetised in the direction of its axis of symmetry, is identical to that of a solenoid of the same dimension with a current density $N'i=\mu$; here, i is a fictitious current as opposed to the current I which we aim to model, with

$$\begin{aligned} \mu =\frac{\mu _0 m}{4\pi }, \end{aligned}$$

(35)

the product of $\mu _0=4\pi \times 10^{-7}\mathrm{H/m}$ the permeability of free space times the magnetic/magnet’s dipole moment m divided by $4\pi$, and $N'$ the number density of the turns per metre (Lorrain and Corson [36], pp. 393). We start with the magnetic flux generated by a current in a single-coil solenoid, cf. [27, 36] (Jackson, pp. 178 and Lorrain and Corson, pp. 319) and subsequently, via integration along the magnet, extend that to an entire solenoid with multiple turns equivalent to our magnet.

In spherical coordinates $(r,\varphi ,\theta )$ and with the centre of the coil placed at the origin, the approximate expressions [27, 36] of the two nonzero components of the magnetic flux, for distances $r\gg A_{\text {m}}$ larger than the radius $A_{\text {m}}$ of the magnet, are given by the spherical-coordinate components $B_r = {2\mu \cos \theta }/{r^3}$, $B_\theta = {\mu \sin \theta }/{r^3}$ of the magnetic flux $\mathbf{B}$, or rewritten in cylindrical coordinates $(\rho ,\phi ,z)$ for the radial cylindrical-coordinate component of the magnetic flux as:

$$\begin{aligned} B_\rho&= B_r\sin \theta +B_\theta \cos \theta = \frac{3\mu z \rho }{(\rho ^2+z^2)^{\frac{5}{2}}}. \end{aligned}$$

(36)

The magnetic field $\mathbf{B}$ is expressed in Teslas, $\mathrm{T}$, the permeability $\mu _0$ of free space in Henry’s per metre, $\mathrm{H/m}=\mathrm{T m}^2/\mathrm{A}$, the dipole moment m in Ampere-square-metre, $\mathrm{A m}^2$, and the radius r in metres. The above holds for an infinitesimally short magnet and far away from the magnet, relative to the distance at which the magnetic flux is measured and relative to the length of the coils, cf. [11] [their equations (1) and (2)]. The magnetic field induced by a magnet of finite length $L_m$ is considered next and reduces in the far field to the above expression.

The magnetic flux $\mathbf{B}$ is related to the magnetic field intensity $\mathbf{H}$ and magnetisation density $\mathbf{M}$ as follows (page 395 of [36]):

$$\begin{aligned} \mathbf{B} = \mu _0(\mathbf{H}+\mathbf{M}). \end{aligned}$$

(37)

In the absence of a current density $\mathbf{J}$, the magnetic field density is irrotational, such that $\mathbf{H}=-\varvec{\nabla }\varPsi$ outside the magnet, with magnetic scalar potential $\varPsi$. Since $\varvec{\nabla }\cdot \mathbf{B}=0$, we find from (37) that $\varvec{\nabla }\cdot \mathbf{H} =-\varvec{\nabla }\cdot \mathbf{M}$ and, therefore, that

$$\begin{aligned} \nabla ^2 \varPsi = -\frac{\rho _{\text {m}}}{\mu _0} \equiv \varvec{\nabla }\cdot \mathbf{M} \end{aligned}$$

(38)

with magnetic charge density $\rho _{\text {m}}$. The integral solution of (38) reads:

$$\begin{aligned} \varPsi = \iiint _{V'} \frac{\rho _m(\mathbf{r}')}{4\pi \mu _0|\mathbf{r}-\mathbf{r}'|}\,{\mathrm d}V'. \end{aligned}$$

(39)

For a magnet uniformly magnetised in the z-direction, we have a magnetisation density $\mathbf{M}=M_0\hat{\mathbf{z}}$ or, alternatively, the magnetic density $\rho _{\text {m}}=0$ throughout the magnet except at the end surfaces where $\rho _{\text {m}}=\pm \,\mu _0 M_0\delta (z' \mp L_{\text {m}}/2)$. The magnetic scalar potential $\varPsi$ is given by the triple integral (39) over the length $L_{\text {m}}$ of the magnet of radius $A_{\text {m}}<a$ with a the radius of the inductor’s coils, cf. [36] (pp. 395) and [26]:

$$\begin{aligned} \varPsi (\rho ,z)&= \frac{M_0}{4\pi } \int _0^{2\pi }\int _{0}^{A_{\text {m}}} R\Biggl ( \frac{1}{(R^2+\rho ^2-2 R \rho \cos \phi +(z-\frac{L_{\text {m}}}{2})^2)^{\frac{1}{2}}}\Bigr .\nonumber \\ \Bigl .&\quad -\Bigl . \frac{1}{\left( R^2+\rho ^2-2 R \rho \cos \phi +\left( z+\frac{L_{\text {m}}}{2}\right) ^2\right) ^{\frac{1}{2}}} \Biggr ) \,{\mathrm d}R\,{\mathrm d}\phi , \end{aligned}$$

(40)

in which, based on symmetry, it suffices to take $\tilde{\phi }=0$ with $x=\rho \cos \tilde{\phi }$ etc., such that $|\mathbf{r}-\mathbf{r}'|^2=(R\cos \phi -\rho )^2+R^2\sin ^2\phi +(z-z')^2$. The expression of the relevant component of the magnetic field evaluated for a magnet of length $L_{\text {m}}$ and radius $A_{\text {m}}<a$ then becomes:

$$\begin{aligned} B_{\rho }(\rho ,z)&= -\mu _0\frac{\partial {\varPsi _{\phi }}}{\partial {\rho }}\nonumber \\&= \frac{\mu _0 M_0}{4\pi }\int _0^{2\pi }\int _0^{A_{\text {m}}} \Biggr ( \frac{R(\rho -R\cos \phi )}{(R^2+\left( \frac{L_{\text {m}}}{2}-z\right) ^2+\rho ^2-2 R \rho \cos \phi )^{\frac{3}{2}}} \nonumber \\&\qquad \qquad -\frac{R(\rho -R\cos \phi )}{(R^2+\left( \frac{L_{\text {m}}}{2}+z\right) ^2+\rho ^2-2 R \rho \cos \phi )^{\frac{3}{2}}} \Biggl ) \,{\mathrm d}R\,{\mathrm d}\phi . \end{aligned}$$

(41)

Far away from the magnet, this radial component can be approximated using Taylor expansions, such that

$$\begin{aligned} B_{\rho }(\rho ,z)&\approx \frac{\mu _0 M_0}{4\pi }\int _0^{2\pi }\int _0^{A_{\text {m}}} \frac{R \rho }{(z^2+\rho ^2)^{\frac{3}{2}}}\Biggr ( \frac{1}{\bigl (1+(-z L_{\text {m}} + \frac{L_{\text {m}}^2}{4})/(z^2+\rho ^2)\bigr )^{\frac{3}{2}}} \nonumber \\&\qquad \qquad -\frac{1}{\bigl (1+(z L_{\text {m}} + \frac{L_{\text {m}}^2}{4})/(z^2+\rho ^2)\bigr )^{\frac{3}{2}}} \Biggl ) \,{\mathrm d}R\,{\mathrm d}\phi \end{aligned}$$

(42a)

$$\begin{aligned}&\approx \frac{\mu _0 M_0}{4\pi }\int _0^{2\pi }\int _0^{A_{\text {m}}} \frac{3 L_{\text {m}} z R \rho }{(z^2+\rho ^2)^{\frac{5}{2}}} \,{\mathrm d}R\,{\mathrm d}\phi \end{aligned}$$

(42b)

$$\begin{aligned}&= \frac{\mu _0 M_0 \pi A_{\text {m}}^2 L_{\text {m}}}{4\pi } \frac{3 z \rho }{(z^2+\rho ^2)^{\frac{5}{2}}}, \end{aligned}$$

(42c)

which equals (36) with (35) when we identify $m = M_0 \pi A_{\text {m}}^2 L_{\text {m}}$ as the magnetic/magnet’s dipole moment with $\pi A_{\text {m}}^2 L_{\text {m}}$ the volume taken up by the magnet. In (41), the magnet is placed in $z\in [-L_{\text {m}}/2,L_{\text {m}}/2]$, while, in our wave-energy device, the magnet resides between $z\in [Z(t)+H_{\text {m}}-L_{\text {m}}/2,Z(t)+H_{\text {m}}+L_{\text {m}}/2]$. Consequently, we need to adapt expression (41) as follows:

$$\begin{aligned} \tilde{B}_{\rho }(\rho ,z)= & {} \frac{\mu _0 M_0}{4\pi }\int _0^{2\pi }\int _0^{A_{\text {m}}} \Biggr ( \frac{R(\rho -R\cos \phi )}{\left( R^2+\left( \frac{L_{\text {m}}}{2}{-}z{+}Z{+}H_{\text {m}}\right) ^2+\rho ^2-2 R \rho \cos \phi \right) ^{\frac{3}{2}}} \nonumber \\&-\frac{R(\rho -R\cos \phi )}{\left( R^2+\left( \frac{L_{\text {m}}}{2}+z-Z-H_{\text {m}}\right) ^2+\rho ^2-2 R \rho \cos \phi \right) ^{\frac{3}{2}}} \Biggl ) \,{\mathrm d}R\,{\mathrm d}\phi \end{aligned}$$

(43a)

$$\begin{aligned}\approx & {} \frac{3\mu \rho (z-Z-H_{\text {m}})}{\left( (z-Z-H_{\text {m}})^2+\rho ^2\right) ^{\frac{5}{2}}}. \end{aligned}$$

(43b)

Second step Placing the magnet in a moving range $z\in [Z(t)+H_{\text {m}}-L_{\text {m}}/2,Z(t)+H_{\text {m}}+L_{\text {m}}/2]$ with length $H_m$ above the centre of mass Z(t) and for fixed coils with N turns and a radius $\rho =a$ over a coil length L over a fixed range $z\in [\bar{Z}+(1+\alpha _h) H_{\text {m}}-L/2,\bar{Z}+(1+\alpha _h) H_{\text {m}}+L/2]$ with $0<\alpha _h<1$, the expression (43a) can be integrated in z over the coil to obtain the coil density [cf. [11] their (6)–(8)]

$$\begin{aligned} \epsilon _1(Z)&= \frac{N}{L}\int _{\bar{Z}+(1+\alpha _h)H_{{\text {m}}}-\frac{L}{2}}^{\bar{Z}+(1+\alpha _h)H_{\text {m}}+\frac{L}{2}} \tilde{B}_{\rho }(\rho =a,z)\,\mathrm{d}z, \end{aligned}$$

(44a)

$$\begin{aligned} \epsilon _1(Z)&= \frac{N}{L}\int _{-\frac{L}{2}}^{\frac{L}{2}} \tilde{B}_{\rho }(\rho =a,z=q+\bar{Z}+(1+\alpha _h) H_{\text {m}})\,\mathrm{d}q \end{aligned}$$

(44b)

$$\begin{aligned}&= \frac{ a \mu N}{L} {G}(Z) \end{aligned}$$

(44c)

$$\begin{aligned}&\approx \frac{N}{L}\int _{-\frac{L}{2}}^{\frac{L}{2}}\frac{3\mu a (q+\bar{Z}+\alpha _h H_{\text {m}}-Z)}{\left( a^2+(q+\bar{Z}+\alpha _h H_{\text {m}}-Z)^2\right) ^{\frac{5}{2}}}\, \,\mathrm{d}q \end{aligned}$$

(44d)

$$\begin{aligned}&= \frac{a \mu N}{L} \Biggl ( \frac{1}{\left( a^2+\left( \bar{Z}+\alpha _h H_{\text {m}}-Z-\frac{L}{2}\right) ^2\right) ^{\frac{3}{2}}} \nonumber \\&\quad \quad -\frac{1}{\left( a^2+\left( \bar{Z}+\alpha _h H_{\text {m}}-Z+\frac{L}{2}\right) ^2\right) ^{\frac{3}{2}}} \Biggr ), \end{aligned}$$

(44e)

where we have used that at the faces of the moving magnet

$$\begin{aligned} \frac{L_{\text {m}}}{2}-z+Z+H_{\text {m}}&= \frac{L_{\text {m}}}{2} -q-\bar{Z}-\alpha _h H_{\text {m}}+Z,\\ \frac{L_{\text {m}}}{2}+z-Z-H_{\text {m}}&= \frac{L_{\text {m}}}{2} +q+\bar{Z}+\alpha _h H_{\text {m}}-Z, \end{aligned}$$

and defined the function

$$\begin{aligned} G(Z)&= \frac{1}{\pi A_{\text {m}}^2 L_{\text {m}} a} \int _{-\frac{L}{2}}^{\frac{L}{2}}\int _0^{2\pi }\int _0^{A_{\text {m}}} \nonumber \\&\qquad \Bigr ( \frac{r(a-r\cos \phi )}{\left( r^2+\left( \frac{L_{\text {m}}}{2}-q-\bar{Z}-\alpha _h H_{\text {m}}+Z\right) ^2+a^2-2 r a \cos \phi \right) ^{\frac{3}{2}}}\Bigr . \nonumber \\&\qquad \Bigl .-\frac{r(a-r\cos \phi )}{\left( r^2+\left( \frac{L_{\text {m}}}{2}+q+\bar{Z}+\alpha _h H_{\text {m}}-Z\right) ^2+a^2-2 r a \cos \phi \right) ^{\frac{3}{2}}} \Bigl ) \,{\mathrm d}r\,{\mathrm d}\phi \,\mathrm{d}q \end{aligned}$$

(44f)

$$\begin{aligned}&\approx \frac{1}{\left( a^2+\left( \bar{Z}+\alpha _h H_{\text {m}}-Z-\frac{L}{2}\right) ^2\right) ^{\frac{3}{2}}}-\frac{1}{\left( a^2+\left( \bar{Z}+\alpha _h H_{\text {m}}-Z+\frac{L}{2}\right) ^2\right) ^{\frac{3}{2}}}, \end{aligned}$$

(44g)

with the latter approximation holding in the far field, starting from (44d) and (43b). Note that only when $\alpha _h=0$ and the water and the buoy–mast–magnet system are at rest, the magnet sits in the middle of the coils. A sketch of the various coordinate systems is given in Fig. 19. A graph of $\gamma G(Z)$ versus Z and its approximation shows that the two functions lie close together, cf. [3].

Fig. 19

Sketch of the magnetic-induction motor set-up: on the left the system when the magnet passes its rest position and on the right away from the rest position

Ohm’s law for a circuit subject to a magnetic flux, moving with a speed $\dot{Z}$ in the vertical, reads:

$$\begin{aligned} \mathbf{J}&= \sigma (\mathbf{E}+\dot{Z}\hat{\mathbf{z}}\,\times \mathbf{B}), \end{aligned}$$

(45)

with current density $\mathbf{J}$, electrical field $\mathbf{E}$, conductivity $\sigma >0$ for a conductor, and unit vector $\hat{\mathbf{z}}$ in the vertical. Integration of Ohm’s law (45) around the coils at $\rho =a$ yields (extending [8, 11]):

$$\begin{aligned} \oint \frac{\mathbf{J}}{\sigma }\cdot {\mathrm{d}}{} \mathbf{l} = \frac{I}{\pi D^2/4}\frac{N 2\pi a}{\sigma } \equiv I R_{\text {c}}&= \int _{-\frac{L}{2}}^{\frac{L}{2}}\oint \mathbf{E}+\dot{Z} \hat{\mathbf{z}}\times \mathbf{B}\cdot {\mathrm{d}}{} \mathbf{l}\,{\mathrm{d}} q\nonumber \\&= -L_i\frac{\mathrm{d}I}{\mathrm{d}t}+2\pi a\, \epsilon _1(Z) \,\dot{Z} \nonumber \\&= -L_i\frac{\mathrm{d}I}{\mathrm{d}t}+ \frac{2\pi a^2 N\mu }{L}\dot{Z} \, G(Z)\nonumber \\&\equiv -L_i\frac{\mathrm{d}I}{\mathrm{d}t}+V_{\text {c}}, \end{aligned}$$

(46)

where $\mathrm{d}{} \mathbf{l}= a\,\mathrm{d}\theta (-\sin \theta ,\cos \theta ,0)^T$ and $\mathbf{B}=\tilde{B}_{\rho }(\cos \theta ,\sin \theta ,0)^T$ with $\theta \in [0,2\pi ]$, inductance $L_i$ of the inductor and the voltage drop $V_{\text {c}}$. Note that the resistance of the coils is defined by $R_{\text {c}}=N (2\pi a)/({\sigma }\pi D^2/4)$ and the current magnitude by $J=I/(\pi D^2/4)$ with D the cross-sectional diameter of the coil. Hence, the circuit equation becomes:

$$\begin{aligned} I(R_{\text {c}}+R_i)&= -L_i\dot{I}+V_{\text {c}}+V_{\text {s}}(I), \end{aligned}$$

(47)

where we have added the resistance $V_{\text {s}}(I)$ (15) of the two (sets of) LEDs modelled using combined Shockley equations, placed in parallel, as well as the resistance $R_i$ of the remaining wires to and from these LEDs. It should be possible to add $I R_i$ and the Shockley voltage $V_{\text {s}}$ directly in Ohm’s law, but we simply added the two terms heuristically.

Faraday’s induction law (chapters 7 and 8 [36]) used above follows from one of the Maxwell’s equations, $\varvec{\nabla }\times \mathbf{E} = -\partial _t\mathbf{B}$, for one circuit as:

$$\begin{aligned} \oint \mathbf{E}\cdot \mathrm{d}{} \mathbf{l}= -\frac{{\mathrm d}}{{\mathrm d}t}\iint _{S}\mathbf{B}\cdot {\mathrm d}\mathbf{a} = -\frac{{\mathrm d}\varPhi }{{\mathrm d}t} = -L_i\dot{I}, \end{aligned}$$

(48)

with induction $\varPhi$, surface S bounded by the path of the line integral, and surface element ${\mathrm d}\mathbf{a}$ on the coils of the inductor. The magnetic induction inside a long solenoid is $B=\mu _0 (N/L) I$ (cf. (8.59) in [36]), such that $\varPhi = \mu _0(N/L) I \pi a^2$ (cf. (8.60) in [36]) and, hence, for N windings $L_i = K \mu _0(N^2/L) \pi a^2$ (cf. (8.61) in [36]). For a long solenoid, $K=1$, and for a short solenoid, $K<1$ with $K=0.53$ for $a/L=1$ (Table 8-1 in [36]).

Third step Faraday’s expression for the magnetic force $\mathbf{F}$, the force on charged particles in the coils as used in the momentum equations of magneto-hydrodynamics, is:

$$\begin{aligned} \mathbf{F}&= \iiint \mathbf{E}+\mathbf{J}\times \mathbf{B}\,\mathrm{d}V = \iiint \mathbf{E} \,\mathrm{d}V+ I\oint \mathrm{d}{} \mathbf{l}\times \mathbf{B}\nonumber \\&= \frac{N}{L}\int _0^{\infty } \int _0^{2\pi } \int _{-\frac{L}{2}}^{\frac{L}{2}} \rho \,I\, \delta (\rho -a)\tilde{B}_{\rho } (-\sin \theta ,\cos \theta ,0)^T \nonumber \\&\quad \times (\sin \theta ,\cos \theta ,0)^T\,\mathrm{d}\rho \,\mathrm{d}\theta \,\mathrm{d}q, \end{aligned}$$

(49)

in which we have replaced the magnitude of $\mathbf{J}$ integrated across a string of coil with area $\varDelta S$ by $I/\varDelta S$ multiplied times $\varDelta S \delta (\rho -a)$ to focus its averaged effect at $\rho =a$ exclusively. Hence, the vertical component $F=\mathbf{F}\cdot \hat{\mathbf{z}}$ of the force between the conducting coils and the magnet is:

$$\begin{aligned} F&= \int _{-\frac{L}{2}}^{\frac{L}{2}} \oint I \mathrm{d}{} \mathbf{l}\times \mathbf{B}\cdot \hat{\mathbf{z}}\, \mathrm{d}q = -\frac{2\pi a^2 N\mu I}{L} G(Z). \end{aligned}$$

(50)

To facilitate further analysis, we momentarily simplify the hydrodynamic force on the buoy, used in the main text, by a mass–spring component with spring constant $k_{\text {s}}$. Combining this simplification with the vertical momentum equation of the simplified buoy–mast system, we then arrive at the following coupled mechanical and magnetical system:

$$\begin{aligned} \dot{Q}&= I, \end{aligned}$$

(51a)

$$\begin{aligned} L_i \dot{I}&= \gamma G(Z)\dot{Z} \underline{-(R_{\text {c}}+R_i) I-\mathrm{sign}(I) n_{\text {q}} V_{\text {T}} \ln {\left( \frac{|I|}{I_{{\text {sat}}}}+1\right) }}, \end{aligned}$$

(51b)

$$\begin{aligned} \dot{Z}&= W, \end{aligned}$$

(51c)

$$\begin{aligned} M\dot{W}&= -M g -k_{\text {s}} Z -\gamma G(Z) I, \end{aligned}$$

(51d)

with constant $\gamma \equiv 2\pi a^2 \mu N/L$ and underlined dissipative terms. When we ignore the self-induction term $L_i\dot{I}$ and the Shockley expression for the LEDs in (51), we note that $(R_{\text {c}}+R_i)I=\gamma G(Z)\dot{Z}$; elimination of I then shows that the magnetic force in the vertical momentum equation (51d) acts as a (nonlinear) drag, proportional to $\dot{Z}$ or W, cf. the linear analogue in [11]. In the absence of the underlined, linear, and nonlinear dissipative terms in (51), the system (51) should be conservative, which will be explored next. In this conservative limit, we first rewrite (51) as:

$$\begin{aligned} L_i \ddot{Q} -\gamma G(Z)\dot{Z}&= 0 \quad \text {and}\quad M\ddot{Z} + M g + k_{\text {s}} Z +\gamma G(Z)\dot{Q} = 0. \end{aligned}$$

(52)

The system (52) has a Lagrangian $\mathsf{L}_{{\text {mm}}}$, defined in and satisfying the following variational principle:

$$\begin{aligned} 0&=\delta \int _0^T \mathsf{L}_{{\text {mm}}}(Z,\dot{Z},Q,\dot{Q})\,\mathrm{d}t \end{aligned}$$

(53a)

$$\begin{aligned}&\equiv \delta \int _0^T \frac{1}{2} M \dot{Z}^2+\frac{1}{2} L_i\dot{Q}^2 -M g Z -\frac{1}{2} k_{\text {s}} Z^2+\gamma G({Z})Q \dot{Z} \,\mathrm{d} t \end{aligned}$$

(53b)

$$\begin{aligned}&= \int _0^T -\left( M \ddot{Z} + M g + k_{\text {s}} Z + \gamma G({Z}) \dot{Q} +\gamma G'(Z)\dot{Z}Q-\gamma G'(Z)\dot{Z}Q\right) \delta Z\nonumber \\&\qquad \qquad +\left( - L_i \ddot{Q} +\gamma G({Z}) \dot{Z} \right) \delta Q \,\mathrm{d} t \end{aligned}$$

(53c)

$$\begin{aligned}&= \int _0^T -\left( M \ddot{Z} + M g + k_{\text {s}} Z + \gamma G({Z}) \dot{Q} \right) \delta Z +\left( - L_i \ddot{Q} +\gamma G({Z}) \dot{Z} \right) \delta Q \,\mathrm{d} t \end{aligned}$$

(53d)

for end-point conditions $\delta Q(0)=\delta Q(T)=\delta Z(0)=\delta Z(T)=0$. The equations of motion in (52) follow from the arbitrariness of the variations in the last expression of (). To facilitate a Legendre transform, the variational principle (53) is rewritten as:

$$\begin{aligned} 0&=\delta \int _0^T \mathsf{L}_{{\text {mm}}}(Z,\dot{Z},Q,\dot{Q})\,\mathrm{d}t \nonumber \\&\equiv \delta \int _0^T \frac{1}{2} M \dot{Z}^2+\frac{1}{2} L_i\dot{Q}^2 -M g Z -\frac{1}{2} k_{\text {s}} Z^2-K({Z})\dot{Q}\,\mathrm{d} t \end{aligned}$$

(54)

with $K(Z)\equiv \int ^{Z}\gamma G(\hat{Z})\,\mathrm{d}\hat{Z}$.

A Legendre transform of (54) yields the following conjugate momenta:

$$\begin{aligned} P_{Q}\equiv \frac{\partial \mathsf{L}_{{\text {mm}}}}{\partial \dot{Q}} = L_i\dot{Q}-K(Z)\quad \text {and}\quad M W \equiv \frac{\partial \mathsf{L}_{{\text {mm}}}}{\partial \dot{Z}} = M\dot{Z}. \end{aligned}$$

(55)

The Hamiltonian $H(Z,W,Q,P_{Q})$ is then the Legendre transform of $\mathsf{L}(Q,\dot{Q},Z,\dot{Z})$ as follows:

$$\begin{aligned} H(Z,W,Q,P_{Q})&= P_{Q}\dot{Q}+M W\dot{Z} - \mathsf{L}_{{\text {mm}}}(Q,\dot{Q},Z,\dot{Z})\nonumber \\&= \frac{1}{2} \frac{\bigl (P_{Q}+K(Z)\bigr )^2}{L_i}+\frac{1}{2} M W^2+Mg Z+\frac{1}{2} k_{\text {s}} Z^2. \end{aligned}$$

(56)

The variational principle (54) in terms of these new variables then becomes:

$$\begin{aligned} 0&= \delta \int _0^T P_{Q}\dot{Q} + M W\dot{Z} - H(Z,W,Q,P_{Q})\,\mathrm{d} t \end{aligned}$$

(57a)

$$\begin{aligned}&= \delta \int _0^T P_{Q}\dot{Q} + M W\dot{Z} - \frac{1}{2} \frac{\bigl (P_{Q}+K(Z)\bigr )^2}{L_i}-M g Z -\frac{1}{2}\left( M W^2+ k_{\text {s}} Z^2\right) \,\mathrm{d} t \end{aligned}$$

(57b)

$$\begin{aligned}&= \int _0^T \left( \dot{Q} -\frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}\right) \varDelta P + (M\dot{Z}-M W)\delta W\nonumber \\&\qquad \qquad -\left( M \dot{W} + M g + k_{\text {s}} Z + K'(Z)\frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}\right) \delta Z -{\dot{P}_{Q}}\delta Q \,\mathrm{d} t, \end{aligned}$$

(57c)

yielding, cf. (52), the system of equations:

$$\begin{aligned} {\delta P_{Q}:}&\quad \dot{Q} = \frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}\equiv I,\qquad {\delta W:} \quad M\dot{Z} = M W \end{aligned}$$

(58a)

$$\begin{aligned} {\delta Q:}&\quad {\dot{P}_{Q}} = 0,\qquad {\delta Z:} \quad M\dot{W}+M g+k_{\text {s}} Z +K'(Z) \frac{\bigl (P_{Q}+K(Z)\bigr )}{L_i}=0. \end{aligned}$$

(58b)

The modification (12) to the variational principle (57) without the potential energy of the spring and, instead, including the hydrodynamics was used in the main text.

A summary of the physical parameters introduced in this appendix and some representative values can be found in Table 5.