Skip to main content
SpringerLink
Log in

Thoughts on the Non-ordinary Peridynamics Model Based on Three-body Potential

  • Original Articles
  • Published:
Journal of Peridynamics and Nonlocal Modeling Aims and scope Submit manuscript

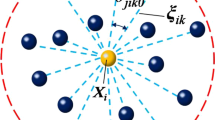
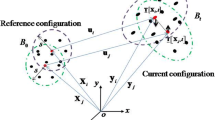
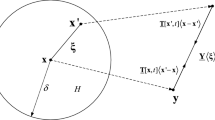
Abstract

This paper studies the internal relationship between peridynamics (PD) models, which address to the Poisson's ratio limitation in original bond-based PD theory by considering tangential bond force or tangential stiffness. Firstly, a non-ordinary state-based PD model is formulated based on a micro-potential considering a more general three-body interaction potential, which can also remove the constraint on values of Poisson’s ratio. Then, a special three-body interaction potential, called novel three-body interaction potential, is adopted in the proposed PD model stated above; it can be found that the resulting PD model can be equivalent to that considering bond stretch and rotation published earlier under assumption of small deformation conditions. This discovery in turn reveals the macroscopic mechanical mechanism of the novel three-body interaction potential in resisting shear deformation. Moreover, the result not only provides a physical explanation for the latter to some extent, but also is helpful to reveal the internal relationships between those PD models considering tangential bond force directly. In addition, another special example of PD model considering distribution of the intensity of long range forces is also given within the proposed PD modeling framework. Its performance is computationally demonstrated by a dynamic fracture problem. These results show that formulating PD models within state-based PD framework by assuming reasonable micro-potential can be proper and flexible in practical engineering problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Availability of Data and Materials

The datasets supporting the conclusions of this article are included within the article and its additional files.

References

  1. Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209

    Article  MathSciNet  MATH  Google Scholar 

  2. Gerstle W, Sau N, Silling SA (2007) Peridynamic modeling of concrete structures. Nucl Eng Des 237:1250–1258

    Article  Google Scholar 

  3. Silling SA, Bobaru F (2005) Peridynamic modeling of membranes and fibers. Int J Non-Linear Mech 40:395–409

    Article  MATH  Google Scholar 

  4. Hu YL, De Carvalho NV, Madenci E (2015) Peridynamic modeling of delamination growth in composite laminates. Compos Struct 132:610–620

    Article  Google Scholar 

  5. Hu YL, Madenci E (2016) Bond-based peridynamic modeling of composite laminates with arbitrary fiber orientation and stacking sequence. Compos Struct 153:139–175

    Article  Google Scholar 

  6. Madenci E, Barut A, Phan N (2018) Peridynamic unit cell homogenization for thermoelastic properties of heterogenous microstructures with defects. Compos Struct 188:104–115

    Article  Google Scholar 

  7. Chen Z, Niazi S, Bobaru F (2019) A peridynamic model for brittle damage and fracture in porous materials. Int J Rock Mech Min Sci 122:104059

    Article  Google Scholar 

  8. Oterkus S, Madenci E, Agwai A (2014) Peridynamic thermal diffusion. J Comput Phys 265:71–96

    Article  MathSciNet  MATH  Google Scholar 

  9. Madenci E, Oterkus S (2016) Oridnary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. J Mech Phys Solids 86:192–219

    Article  MathSciNet  Google Scholar 

  10. Zhang Y, Madenci E (2021) A coupled peridynamic and finite element approach in ANSYS framework for fatigue life prediction based on the kinetic theory of fracture. J Peridyn Nonlocal Model 4:51–87

    Article  MathSciNet  Google Scholar 

  11. Bang DJ, Ince A, Oterkus E, Oterkus S (2021) Crack growth modeling and simulation of a peridynamic fatigue model based on numerical and analytical solution approaches. Theor Appl Fract Mech 114:103026

    Article  Google Scholar 

  12. Hu YL, Madenci E (2017) Peridynamics for fatigue life and residual strength prediction of composite laminates. Compos Struct 160:169–184

    Article  Google Scholar 

  13. Madenci E, Barut A, Yaghoobi A, Phan N, Fertig RS (2021) Combined peridynamics and kinetic theory of fracture for fatigue failure of composites under constant and variable amplitude loading. Theor Appl Fract Mech 112:102824

    Article  Google Scholar 

  14. Jafarzadeh S, Chen Z, Bobaru F (2018) Peridynamic modeling of intergranular corrosion damage. J Electrochem Soc 165(7):362–374

    Article  Google Scholar 

  15. Kulkarni SS, Tabarraei A (2020) An ordinary state based peridynamic correspondence model for metal creep. Eng Fract Mech 233:107042

    Article  Google Scholar 

  16. Deng X, Wang B (2020) Peridynamic modeling of dynamic damage of polymer bonded explosive. Comput Mater Sci 173:109405

    Article  Google Scholar 

  17. Madenci E, Dorduncu M, Barut A, Futch M (2017) Numerical solution of linear and nonlinear partial differential equations using the peridynamic differential operator. Numer Methods Partial Differ Equ 33:1726–1753

    Article  MathSciNet  MATH  Google Scholar 

  18. Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17):1526–1535

    Article  Google Scholar 

  19. Silling SA, Epton M, Weckner O, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151–184

    Article  MathSciNet  MATH  Google Scholar 

  20. Silling SA (2017) Stability of peridynamic correspondence material models and their particle discretizations. Comput Methods Appl Mech Eng 322:42–57

    Article  MathSciNet  MATH  Google Scholar 

  21. Li P, Hao Z, Zhen W (2018) A stabilized non-ordinary state-based peridynamic model. Comput Methods Appl Mech Eng 339:262–280

    Article  MathSciNet  MATH  Google Scholar 

  22. Breitzman T, Dayal K (2018) Bond-level deformation gradients and energy averaging in peridynamics. J Mech Phys Solids 110:192–204

    Article  MathSciNet  Google Scholar 

  23. Le Q, Chan WK, Schwartz J (2014) A two-dimensional ordinary, state-based peridynamic model for linearly elastic solids. Int J Numer Meth Eng 98(8):547–561

    Article  MathSciNet  MATH  Google Scholar 

  24. Madenci E, Oterkus E (2014) Peridynamic Theory and Its Application. Springer, New York, pp 53–74

    Book  MATH  Google Scholar 

  25. Tupek MR, Radovitzky R (2014) An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. J Mech Phys Solids 65:82–92

    Article  MathSciNet  MATH  Google Scholar 

  26. Chen H (2018) Bond-associated deformation gradients for peridynamic correspondence model. Mech Res Commun 90:34–41

    Article  Google Scholar 

  27. Chen H, Spencer BW (2019) Peridynamic bond-associated correspondence model: Stability and convergence properties. Int J Numer Meth Eng 117:713–727

    Article  MathSciNet  Google Scholar 

  28. Chan WL, Chen H (2021) Peridynamic bond-associated correspondence model: Wave dispersion property. Int J Numer Meth Eng 122(18):4848–4863

    Article  MathSciNet  Google Scholar 

  29. Zheng G, Shen G, Xia Y, Hu P (2020) A bond-based peridynamic model considering effects of particle rotation and shear influence coefficient. Int J Numer Meth Eng 121:93–109

    Article  MathSciNet  Google Scholar 

  30. Hu YL, Madenci E (2016) Bond-based peridynamics with an arbitrary Poisson’s ratio. In: American Institute of Aeronautics and Astronautics 57th AIAA/ASCE/AHS/ASC structures, structural dynamics, and materials conference, San Diego, California, USA

  31. Wang Y, Zhou X, Wang Y, Shou Y (2017) A 3-D conjugated bond-pair-based peridynamic formulation for initiation and propagation of cracks in brittle solids. Int J Solids Struct 134:1–27

    Google Scholar 

  32. Huang X, Li S, Jin Y, Yang D, Su G, He X (2019) Analysis on the influence of Poisson’s ratio on brittle fracture by applying uni-bond dual-parameter peridynamic model. Eng Fract Mech 222:106685

    Article  Google Scholar 

  33. Li S, Lu H, Jin Y, Sun P, Huang X, Bie Z (2021) An improved unibond dual-parameter peridynamic model for fracture analysis of quasi-brittle materials. Int J Mech Sci 204:106–571

    Google Scholar 

  34. Huang D, Lu G, Qiao P (2015) An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis. Int J Mech Sci 94:111–122

    Article  Google Scholar 

  35. Zhu Q, Ni T (2017) Peridynamic formulations enriched with bond rotation effects. Int J Eng Sci 121:118–129

    Article  MathSciNet  MATH  Google Scholar 

  36. Li W, Zhu Q, Ni T (2020) A local strain-based implementation strategy for the extended peridynamic model with bond rotation. Comput Methods Appl Mech Eng 358:112–625

    MathSciNet  MATH  Google Scholar 

  37. Madenci E, Barut A, Phan N (2021) Bond-Based Peridynamics with stretch and rotation kinematics for opening and shearing modes of fracture. J Peridyn Nonlocal Model 3:211–254

    Article  MathSciNet  Google Scholar 

  38. Mayo SL, Olafson BD, Goddard WA (1990) DREIDING: A generic force field for molecular simulations. J Phys Chem 94(26):8897–8909

    Article  Google Scholar 

  39. Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44(10):73–168

    Article  Google Scholar 

  40. Li X, Huang Z (2020) A non-ordinary state-based peridynamic constitutive model based on three-body interaction potential and its implementation on algorithm. J Peridyn Nonlocal Model 2(12–13):1–26

    MathSciNet  Google Scholar 

  41. Gurtin E (1981) An Introduction to Continuum Mechanics. Academic Press

    MATH  Google Scholar 

  42. T. Foster J., Silling S.A., Chen, W. (2011) An Energy based failure criterion for use with peridynamic states. J Multiscale Comput Eng 9(6):675–687

    Article  Google Scholar 

  43. Field JE (1992) Hot spot ignition mechanisms for explosives. Acc Chem Res 25:489–496

    Article  Google Scholar 

  44. Ha YD, Bobaru F (2010) Studies of dynamic crack propagation and crack branching with peridynamics. Int J Fract 162:229–244

    Article  MATH  Google Scholar 

  45. Belytschko T, Chen H, Xu J, Zi G (2003) Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment. Int J Numer Meth Eng 58(12):1873–1905

    Article  MATH  Google Scholar 

  46. Bobaru F, Zhang G (2015) Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int J Fract 196(1–2):59–98

    Article  Google Scholar 

  47. Wang X, Kulkarni SS, Tabarraei A (2019) Concurrent coupling of peridynamics and classical elasticity for elastodynamic problems. Comput Methods Appl Mech Eng 344:251–275

    Article  MathSciNet  MATH  Google Scholar 

  48. Bowden FP, Brunton JH, Field JE, Heyes Ad (1967) Controlled fracture of brittle solids and interruption of electrical current. Nature 216:38–42

    Article  Google Scholar 

Download references

Acknowledgements

We thank Dr. Pan Li of China Academy of Engineering Physics for useful discussions. The supports from China Academy of Engineering Physics Institute of Systems Engineering are gratefully acknowledged. The authors would like to thank the editor and reviewer for valuable comments and suggestions.

Author information

Authors and Affiliations

  1. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang, 621999, Sichuan, China

    Xiaolong Li & Zhiming Hao

  2. Shock and Vibration of Engineering Materials and Structures Key Laboratory of Sichuan Province, Mianyang, 621999, Sichuan, China

    Zhiming Hao

Authors
  1. Xiaolong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhiming Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhiming Hao.

Ethics declarations

Competing Interests

The authors declare that they have no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A Proof for Eq. (24)

Proof

By using Eq. (17), (19), we arrive at

$$\begin{array}{l}\mathbf{e}=\left(\mathbf{u}\left({\mathbf{X}}_{j}\right)-\mathbf{u}\left({\mathbf{X}}_{i}\right)\right)\cdot {\varvec{\upchi}}\otimes{\varvec{\upchi}}=\frac{{{\varvec{\upxi}}}_{ij}\cdot \left({\varvec{\upvarepsilon}}+{\varvec{\upomega}}\right)\cdot {{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}{\varvec{\upchi}}\\\;\;\; =\frac{{{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\cdot \left({\varvec{\upvarepsilon}}+{\varvec{\upomega}}\right)\cdot \frac{{{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\left|{{\varvec{\upxi}}}_{ij}\right|{\varvec{\upchi}}=\frac{{{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\cdot {\varvec{\upvarepsilon}}\cdot \frac{{{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\left|{{\varvec{\upxi}}}_{ij}\right|{\varvec{\upchi}}\approx s\left|{{\varvec{\upxi}}}_{ij}\right|{\varvec{\upchi}}.\end{array}$$

Then,

$$\overline{\mathbf{e}}\approx s{\varvec{\upchi} },$$

with \(s\approx {\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\) under small deformation and \({\varvec{\upchi}}\cdot {\varvec{\upomega}}\cdot {\varvec{\upchi}}\)=0. Therefore, \({s}^{2}=\overline{\mathbf{e} }\cdot \overline{\mathbf{e} }\) in Eq. (24) is satisfied.

Appendix B Proof for Eq. (52)

Proof

By Eq. (23)

$$\begin{array}{l}\mathbf{r}\cdot \mathbf{r}=\left(\frac{\left(\mathbf{I}-{\varvec{\upchi}}\otimes{\varvec{\upchi}}\right)\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\cdot \left(\frac{\left(\mathbf{I}-{\varvec{\upchi}}\otimes{\varvec{\upchi}}\right)\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\\\qquad =\left(\frac{\mathbf{I}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}\right)}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\cdot \left(\frac{\mathbf{I}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}\right)}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\\\qquad =\left(\frac{{\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}\right)}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\cdot \left(\frac{{\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {{\varvec{\upxi}}}_{ij}\right)}{\left|{{\varvec{\upxi}}}_{ij}\right|}\right)\\\qquad =\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-{\varvec{\upchi}}\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\right),\end{array}$$

under small deformation conditions, note that \(s\approx {\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\), then

$$\begin{array}{l}\mathbf{r}\cdot \mathbf{r}=\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-{\varvec{\upchi}}s\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-{\varvec{\upchi}}s\right)\\\qquad =\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)-s{\varvec{\upchi}}\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)-\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left(s{\varvec{\upchi}}\right)+s{\varvec{\upchi}}\cdot \left({\varvec{\upchi}}s\right)\\\qquad =\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)- s{\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-\left({\varvec{\upchi}}\cdot {{\varvec{\upvarepsilon}}}^{\mathrm{T}}\right)\cdot \left(s{\varvec{\upchi}}\right)+{s}^{2}\\\qquad =\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)- s{\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}-s\left({\varvec{\upchi}}\cdot {\varvec{\upvarepsilon}}\right)\cdot {\varvec{\upchi}}+{s}^{2}\\\qquad =\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)-{s}^{2},\end{array}$$

which implies \(\mathbf{r}\cdot \mathbf{r}+{s}^{2}=\left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\cdot \left({\varvec{\upvarepsilon}}\cdot {\varvec{\upchi}}\right)\), i.e., Eq. (52) holds.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, X., Hao, Z. Thoughts on the Non-ordinary Peridynamics Model Based on Three-body Potential. J Peridyn Nonlocal Model 4, 398–419 (2022). https://doi.org/10.1007/s42102-022-00084-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42102-022-00084-3

Keywords

Search

Navigation