1 Backgound

In this section, we give a brief historical overview of the development of peridynamics, as far as possible using the notation of previous authors. However, in Section 2, which follows this background, we assume that the reader is not already familiar with this theoretical domain and more comprehensive definitions and derivations are presented. A summary of the symbols, variable names and nomenclature that is used in the paper is compiled in Appendix 1,  Table 2. 

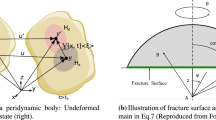
Peridynamics is a non-local continuum theory that was developed for the simulation of fracture phenomenon for brittle materials and was introduced by Silling in 2000 [3]. As opposed to other techniques, peridynamics does not require cracks to be predefined but rather to appear in a spontaneous fashion from an initial intact domain. Unlike classical continuum mechanics which rely on the evaluation of partial derivatives, peridynamics works by replacing the differentiation with integration which remains valid also in the presence of discontinuities. The peridynamics continuum is approximated with a finite set of material points with intermediate bonds. Each material point is connected by bonds to the neighbouring material points within a distance \(\delta\) which defines a horizon \(\mathcal {H}\) which is circular in 2D and spherical in 3D. The force in a bond is related to the bond deformation and the choice of constitutive model. The peridynamics theory was developed on the basis of regular material point distribution which may lead to computationally costly simulations. Additions have been made to enable variable material point distribution for homogeneous materials in [4, 5] and [6] with the motivation to reduce computational cost (see Fig. 1). However, these additions complicates the theory and an argument is presented here for a potentially simpler approach where the bond force is based on the theory of Smooth Particle Hydrodynamics (SPH).

Fig. 1
figure 1

A rectangular subregion of a continuum with varying sized volume elements associate with material points. The bonds are drawn for a material point \(\mathbf {x}\) within the horizon \(\mathcal {H}_x\) which is defined by the radius \(\delta _x\)

Full size image

The equation of motion of a material point in classical continuum mechanics according to Newton’s second law of motion is,

$$\begin{aligned} \rho (\mathbf {x})\ddot{u}(\mathbf {x},t) = \nabla \varvec{\upsigma } + \mathbf {b}(\mathbf {x},t), \end{aligned}$$
(1)

in which the gradient of the stress tensor \(\nabla \varvec{\upsigma }\) is replaced in the peridynamic formulation with an integration of force density,

$$\begin{aligned} \rho (\mathbf {x}){\ddot{u}}(\mathbf {x},t) = \int _{\mathcal {H}_x} \mathbf {f}(\mathbf {x}, \mathbf {x}^{\prime }, t) dV_{x^{\prime }} + \mathbf {b}(\mathbf {x},t), \end{aligned}$$
(2)

which does not rely on assumptions of spatial continuity, and thus enables simulation of phenomena such as fracture. Here \(\rho\) is the material density, \({\ddot{u}}(\mathbf {x},t)\) is the acceleration of a material point at position \(\mathbf {x}\) at time t, \(\mathbf {f}\) is a bond force density acting between two particles at positions \(\mathbf {x}\) and \(\mathbf {x}^\prime\), \(dV_{x^\prime }\) is the volume associated with particle \(\mathbf {x}^\prime\) and \(\mathbf {b}\) is the external loading.

The calculation of the force density \(\mathbf {f}\) varies with the different peridynamic formulations, which are typically classified in terms of bond based, ordinary state-based and non-ordinary state-based theory as described in [7]. Silling introduced the bond based theory in [3], and following the notation in [7], where \(\mathbf {x}\) and \(\mathbf {y}\) represents initial and displaced position of a material point, the bond force is formulated as

$$\begin{aligned} \mathbf {f}(\mathbf {x}, \mathbf {x}^{\prime }, t)^\mathrm {BB} = c s \frac{\mathbf {y^\prime }-\mathbf {y}}{ |\mathbf {y^\prime }-\mathbf {y}|} \mathrm {,} \end{aligned}$$
(3)

where \(\mathbf {y}^{\prime }\) is the displaced position of a particle with initial position \(\mathbf {x}^{\prime }\). The constitutive model is introduced with the micro modulus c, which is calculated from,

$$\begin{aligned} c = \frac{12E}{\pi \delta ^{4}} \mathrm {,} \end{aligned}$$
(4)

where E is the Young’s modulus, \(\delta\) is the radius of the horizon \(\mathcal {H}_x\). The bond stretch s in Eq. (3) is calculated from,

$$\begin{aligned} s = \frac{|\mathbf {y}^{\prime }-\mathbf {y}|- |\mathbf {x}^{\prime }-\mathbf {x}|}{|\mathbf {x}^{\prime }-\mathbf {x}|}. \end{aligned}$$
(5)

Ordinary state-based peridynamics (OSB-PD) was introduced by Silling et. al in 2007 [8] and can be understood as a generalisation of the bond based theory where the limitation of fixed Poisson’s ratio is overcome. The OSB-PD builds on the concept of a state which can be described as a mapping. For the application in solid mechanics the deformation state and the force state are the most central concepts for which definitions and derivation are given in [8]. The equivalent expression for the force density in Eq. (1) as outlined for bond-based theory in Eq. (3) but instead for the OSB-PD theory is according to [7] given as,

$$\begin{aligned} \mathbf {f}(\mathbf {x}, \mathbf {x}^{\prime }, t)^\mathrm {OSB} = \underline{\mathbf {T}}[\mathbf {x},t]\langle \mathbf {x}^{\prime } -\mathbf {x}\rangle - \underline{\mathbf {T}}[\mathbf {x}^{\prime },t]\langle \mathbf {x} -\mathbf {x}^{\prime }\rangle \mathrm {,} \end{aligned}$$
(6)

where \(\underline{\mathbf {T}}\langle \rangle\) is the force state acting on the vector \(\varvec{x}^{\prime } -\varvec{x}\) within the angle brackets. For a linear elastic isotropic material the force state is according to [7] given by,

$$\begin{aligned} \underline{\mathbf {T}}[\mathbf {x},t]\langle \mathbf {x}^{\prime } -\mathbf {x}\rangle = \left( \frac{2 a d \delta }{|\mathbf {x}^\prime - \mathbf {x}|}\mathbf {\theta }(\mathbf {x},t) + bs \right) \frac{\mathbf {y}^\prime - \mathbf {y}}{|\mathbf {y}^\prime - \mathbf {y}|} \end{aligned}$$
(7)

where a, b and d are peridynamic parameters and \(\theta (\mathbf {x},t)\) is the dilatation term.

Smooth particle hydrodynamics is another meshless methods that has be used for similar problems. It was introduced in 1977 by Monaghan et al [9] and the first use of SPH for the simulation of solids was carried out by Libersky and Petschek in 1991 [10]. Just like with peridynamics, the SPH continuum is discretised with a set of particles and each particle is influenced by all neighbours within reach of a kernel function. The similarities between peridynamics and SPH is explored by Ganzenmuller et al in [11]. Following the notation in [12] the equation for the motion of a particle in a continuum with the SPH formulation can be written as,

$$\begin{aligned} \rho \frac{\mathrm {d}v^i}{\mathrm {d}t} = \frac{\partial \sigma ^{ij}}{\partial x^j} + g^i \mathrm {,} \end{aligned}$$
(8)

where \(\rho\) is the material density, \(v^i\) is the \(i^\mathrm {th}\) component of the velocity, \(\sigma ^{ij}\) is the stress tensor, \(x_j\) is the \(j^\mathrm {th}\) cartesian component of the position vector and \(g^i\) denotes the \(i^\mathrm {th}\) component of the body force per unite mass. This expression is developed in [12] Eq.(3.1) into,

$$\begin{aligned} \frac{\mathrm {d}v_a^i}{\mathrm {d}t} = \sum _{b}m_b \left( \frac{\sigma ^{ij}_a}{\rho ^2_a} + \frac{\sigma ^{ij}_b}{\rho ^2_b} + \Pi _{ab}\delta ^{ij} \right) \frac{\partial W_{ab}}{ \partial x^j_a} + g^i \mathrm {,} \end{aligned}$$
(9)

where \(W_{ab}\) is the kernel for a bond between particles a and b, \(m_b\) is the mass of particle b, \(\Pi _{ab}\) and \(\delta ^{ij}\) are terms related to viscosity. The summation acts over all particles b that are within reach of the kernel function, i.e the SPH-horizon. If we simplify Eq. (9) by ignoring body load and the viscosity term (which is mainly relevant for fluid problems) and we multiply both sides with the mass of particle a and focus the attention on the bond between the a and b, the \(i^{\mathrm {th}}\) component of the force \(\mathbf {f}_{ab}\) acting on particle a can be interpreted as

$$\begin{aligned} f^i_{ab} = m_a m_b \left( \frac{\sigma ^{ij}_a}{\rho ^2_a} + \frac{\sigma ^{ij}_b}{\rho ^2_b} \right) \frac{\partial W_{ab}}{ \partial x^j_a}. \end{aligned}$$
(10)

The same bond generates a force of opposite direction and magnitude on particle b, such that

$$\begin{aligned} \mathbf {f}_{ab} = -\mathbf {f}_{ba}. \end{aligned}$$
(11)

Equation (10) seems to lend it self for variable size of particles a and b since the masses, stress, and densities are separate entities. However, the kernel function \(W_{ab}\left( \mathbf {r} -\mathbf {r_b}, h\right)\) which in [13] is defined as a function of \(\mathbf {r}, \mathbf {r_b}\) and h is the same for both particles and need to be separated into \(W_{ab}\) and \(W_{ba}\), allowing for different values of the particle size parameter h.

2 Introduction to the Fibre Model

Fig. 2
figure 2

Particles and arms on the left, fibre mat centre and continuum right. A knowledge of the arm forces implies a unique set of fibre tensions and compressions which implies a unique stress in the continuum. But the reverse does not apply

Full size image

In meshless methods such as aforementioned smoothed particle hydrodynamics (SPH) [9, 13, 14] and peridynamics [3], a fluid or solid continuum is approximated by a system of particles in which each particle is joined by arms to its near neighbours. The forces in the arms are used to model the state of stress in the continuum and it is usual to assume only axial tensile and compressive forces in the arms, although in non-ordinary state based peridynamics [8] non-axial forces in the arms are allowed, effectively producing bending moments in the arms. We will limit our discussion to the case when there are only axial forces.

The left-hand image in Fig. 2 shows a collection of particles and arms. The particles are arranged randomly, but with a limit on the minimum spacing. The arms are shown grayscale with the darkness proportional to the weighting \(\omega _{ab}\) in Eq. (41).

The axial force in a particular arm depends upon:

  1. 1.

    the local state of stress in the continuum that we are modelling,

  2. 2.

    the orientation of the arm relative to the state of stress,

  3. 3.

    the size of the particles at its ends and

  4. 4.

    the length of the arm. Usually, longer arms and shorter arms will carry less force than those somewhere in the middle.

The reasons for criterion 4 are that we want the forces to die away smoothly as we consider further away particles and large forces in short arms cause problems due to the change in force as an arm rotates due to transverse displacements. Or, to put it another way, the geometric stiffness of an arm is the tension divided by the length, which is large for short members, unless the tension is small. A compression produces a negative geometric stiffness. In the following, we shall use the word ‘tension’ to mean tension or compression, if its value is negative.

The assumption is that we have a sufficiently large number of particles and arms to model a continuum with sufficient accuracy. The problem is compounded by the fact that the system of arms and particles is highly statically indeterminate and many different distributions of arm tension will be equivalent to the same stress. We therefore have to make some further assumptions to make the problem determinate. However, if all the arms are in tension, or all the arms are in compression then the sum of the product of the arm forces times their lengths is independent of the arm arrangement [15, 16]. This can be easily shown using virtual work with a virtual uniform dilatation.

In SPH and peridynamics [11] it is usual to derive expressions for the arm tensions by focusing attention on the divergence of the stress tensor, that is how the stress changes with position and hence causes acceleration of the continuum. This approach produces some mathematical complexity which is beyond most engineers who are happier with the ideas behind the finite element as first described by Turner et al. [17].

We will therefore use simpler ideas based on resolution of forces, which we can do if we separate consideration of criteria 1 and 2 listed above from consideration of criteria 3 and 4. The approximation usually introduced in finding the derivative of functions in SPH and peridynamics is replaced by the approximation in replacing summations by integrals. However, the resulting expressions are identical, at least for simple states of stress corresponding to elasticity, fluid pressure or viscosity.

3 Virtual Random Fibre Mat

Regardless of how arm tensions are derived in SPH and peridynamics, it is always assumed that the change of stress is small over distances comparable with the particle spacing. We will therefore consider the situation of a continuum under stress that varies with direction, but not position. But rather than consider a system of particles and arms, we will begin by considering a mat of long random continuous fibres in 2D as shown in the central image in Fig. 2, or the three-dimensional equivalent in which the fibres are randomly arranged in 3D.

Even though the fibres are arranged randomly, we assume that on average the number within a cone of a certain solid angle is the same in all directions.

We assume that there are a large number of fibres, sufficient to model a constant state of stress. At this stage we make no assumption as to what causes the stress. We could use the fibres to represent an elastic or plastic solid or a fluid with pressure and viscosity. This theory is therefore equally applicable to SPH and peridynamics.

We will be discussing stress in 2 and 3 dimensions, and it is important to remember that stress has the units force per unit length in 2D and force per unit area in 3D.

Our model is similar to a fibre reinforced composite, but without the matrix. We do not need a matrix because we are assuming that the stress does not vary with position, only with orientation and that the fibres do not stop and restart. See Hashin [18] for a discussion of composites. When we introduce particles later, the stress will then be able to vary with position, exactly like any other pin jointed framework.

The force in a fibre in a particular direction will depend upon the state of stress and the orientation of the fibre relative to the stress, that is criteria 1 and 2 above. It will also depend upon the number of fibres, as expressed by the total length of fibres per unit area in 2D or volume in 3D. Let us imagine that we double the number of fibres. The total length of fibres will also be doubled, but the force in each fibre will be halved. Thus the sum of the length of each fibre times the force it is carrying per unit area in 2D or volume in 3D will be unchanged. Force times length per unit volume or area has the same units as stress in 3D and 2D respectively.

The arrows in Fig. 1 refer to the fact that a knowledge of the peridynamic arm forces implies a unique set of fibre tensions which implies a unique stress in the continuum. But the reverse does not apply. The peridynamic arms forces depend upon the kernel which gives arm forces dependent upon the arm length. In the case of the fibre mat, different variations of fibre tension with orientation can give rise to the same state of stress in the equivalent continuum.

3.1 Force Flux Density

Let us introduce a quantity which we shall call the force flux density, S, which is a function of the state of stress and the fibre orientation relative to that state of stress. In 2D it is given by

$$\begin{aligned} S=\frac{\pi }{2}TL\mathrm {\quad in \; 2 \; dimensions} \end{aligned}$$
(12)

where T is the tension in each fibre in a particular direction and L is the total length of the fibres per unit area. In 3D it is

$$\begin{aligned} S=\frac{2\pi }{3}TL\mathrm {\quad in \; 3 \; dimensions} \end{aligned}$$
(13)

where L is now the total length of the fibres per unit volume. L has unit one over length in 2D and one over length squared in 3D. Therefore, in both cases, S has the dimensions of stress. In 2D, the fibres contained within the angle from \(\theta\) to \(\theta +d\theta\) would be considered to be the same as the fibres contained in the angle from \(\pi +\theta\) to \(\pi +\theta +d\theta\). Therefore all the fibres would be contained within an angle of \(\pi\) radians. Similarly, all the fibres in 3D would be contained within a hemisphere, that is a solid angle of \(2\pi\) steradians. Thus, in general the tension in a fibre is given by

$$\begin{aligned} T=\frac{NS}{\left( N-1\right) \pi L} \end{aligned}$$
(14)

in N dimensions, \(N=2\) or \(N=3\). Note that S and T will in general vary with direction, whereas L is not associated with a direction. We will see that the reason for choosing the constant in this way is so that when S is isotropic, then its value is equal to the mean stress.

If we want to calculate S for a given state of stress, the problem is statically indeterminate, as we have already noted, and we would have to make certain assumptions. The reverse procedure requires no assumptions since a given S as a function of direction corresponds to a unique state of stress, which we can find by resolving an area into a particular direction and then resolving the corresponding force. In 2 dimensions, this double resolving produces a product of cosines and/ or sines in exactly the same way as in producing the Mohr’s circle for stress [19] to give

$$\begin{aligned} \varvec{\upsigma }= & {} \ \sigma _x\mathbf {ii} + \tau _{xy}\mathbf {ij} + \tau _{yx}\mathbf {ji} + \sigma _y\mathbf {jj} \nonumber \\= & {} \ \frac{2}{\pi }\int _{0}^{\pi }S\left( \theta \right) \left( \cos ^2\theta \mathbf {ii} + \cos \theta \sin \theta \left( \mathbf {ij} + \mathbf {ji}\right) + \sin ^2\theta \mathbf {jj}\right) d\theta \mathrm {.} \end{aligned}$$
(15)

Where \(\mathbf {i}\), \(\mathbf {j}\) and \(\mathbf {k}\) are unit vectors in the directions of the coordinate axes and \(\mathbf {ij}\) indicates the dyadic product, also known as the outer product or tensor product of \(\mathbf {i}\) and \(\mathbf {j}\), and sometime written as \(\mathbf {i}\otimes \mathbf {j}\). In 3 dimensions, the resolving is slightly more complicated,

$$\begin{aligned} \varvec{\upsigma }= & {} \ \sigma _x\mathbf {ii} + \tau _{xy}\mathbf {ij} + \tau _{xz}\mathbf {ik} \nonumber \\&+\tau _{yx}\mathbf {ji} + \sigma _y\mathbf {jj} + \tau _{yz}\mathbf {jk}\nonumber \\&+\tau _{zx}\mathbf {ki} + \tau _{zy}\mathbf {kj} + \sigma _z\mathbf {kk}\nonumber \\= & {} \ \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } S\left( \theta ,\phi \right) \begin{pmatrix}\left( \sin \phi \left( \cos \theta \mathbf {i} + \sin \theta \mathbf {j}\right) + \cos \phi \mathbf {k}\right) \\ \otimes \left( \sin \phi \left( \cos \theta \mathbf {i} + \sin \theta \mathbf {j}\right) + \cos \phi \mathbf {k}\right) \end{pmatrix} d\theta \sin \phi \,d\phi \nonumber \\= & {} \ \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } S \begin{pmatrix} \sin ^2\phi \begin{pmatrix}\cos ^2\theta \mathbf {ii} + \cos \theta \sin \theta \left( \mathbf {ij}+\mathbf {ji}\right) \\ +\sin ^2\theta \mathbf {jj} \end{pmatrix} \\ + \cos ^2\phi \mathbf {kk} \\ +\sin \phi \cos \phi \begin{pmatrix}\cos \theta \left( \mathbf {ki}+\mathbf {ik}\right) \\ + \sin \theta \left( \mathbf {jk}+\mathbf {kj}\right) \end{pmatrix} \end{pmatrix} d\theta \sin \phi \,d\phi \mathrm {,} \end{aligned}$$
(16)

where \(\phi\) is the angle from the z direction in spherical polar coordinates. The reason for the \(\sin \phi\) between the \(d\theta\) and the \(d\phi\) is that \(d\theta \sin \phi d\phi\) is an element of solid angle, that is surface area on the unit sphere. Thus, for example, taking the \(\mathbf {jk}\) and \(\mathbf {kj}\) components from both sides,

$$\begin{aligned} \tau _{yz}=\tau _{zy} = \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } S\left( \theta ,\phi \right) \cos \theta \,d\theta \sin ^2\phi \cos \phi \,d\phi \mathrm {.} \end{aligned}$$
(17)

The force \(\mathbf {f}\) crossing a cut in 3D specified by the vector \(\mathbf {A}\) whose magnitude is equal to the area of the cut and whose direction is normal to the cut is given by

$$\begin{aligned} \mathbf {f}= & {} \ \mathbf {A}\cdot \varvec{\upsigma }\nonumber \\= & {} \ A_x\left( \sigma _x\mathbf {i} + \tau _{xy}\mathbf {j} + \tau _{xz}\mathbf {k}\right) +A_y\left( \tau _{yx}\mathbf {i} + \sigma _y\mathbf {j} + \tau _{yz}\mathbf {k}\right) +A_z\left( \tau _{zx}\mathbf {i} + \tau _{zy}\mathbf {j} + \sigma _z\mathbf {k}\right) \nonumber \\= & {} \ \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } \begin{pmatrix} S\left( \theta ,\phi \right) \left( \sin \phi \left( \cos \theta A_x + \sin \theta A_y\right) + \cos \phi A_z\right) \\ \left( \sin \phi \left( \cos \theta \mathbf {i} + \sin \theta \mathbf {j}\right) + \cos \phi \mathbf {k}\right) \end{pmatrix} d\theta \sin \phi \,d\phi \mathrm {.} \end{aligned}$$
(18)

We first resolve \(\mathbf {A}\) in the direction specified by \(\theta\) and \(\phi\) and then resolve the force so produced into the coordinate directions. The integral is required to sum the forces from the fibres in different directions.

The force flux density S associates a scalar with each direction in space, but it is clearly more than a vector or tensor field since the values of the scalar associated with each direction are completely independent. When we come to consider plasticity we will find that some directions will be yielding while other directions are still elastic.

3.2 Isotropic Stress

If S is independent of orientation in Eq. (15) we obtain

$$\begin{aligned} \varvec{\upsigma }= S\left( \mathbf {ii} + \mathbf {jj}\right) \mathrm {,} \end{aligned}$$
(19)

in 2D because the average value of \(\cos ^2\theta\) and \(\sin ^2\theta\) is \(\frac{1}{2}\), whereas the average value of \(\cos \theta \sin \theta\) is zero. If S is independent of orientation in Eq. (16),

$$\begin{aligned} \varvec{\upsigma }= & {} \ \ 3S\int _{0}^{\frac{\pi }{2}} \left( \frac{\sin ^2\phi }{2}\left( \mathbf {ii} + \mathbf {jj}\right) + \cos ^2\phi \mathbf {kk}\right) \sin \phi d\phi \nonumber \\= & {} \ \ 3S \left[ \left( \frac{\cos ^3\phi }{6}-\frac{\cos \phi }{2}\right) \left( \mathbf {ii} + \mathbf {jj}\right) - \frac{\cos ^3\phi }{3}\mathbf {kk}\right] _{0}^{\frac{\pi }{2}} \nonumber \\= & {} \ \ S\left( \mathbf {ii} + \mathbf {jj} + \mathbf {kk}\right) \mathrm {,} \end{aligned}$$
(20)

in 3D. Thus, in both 2 and 3D, we find that the mean stress is equal to S, when S is isotropic. Even when S is not isotropic, the mean value of S is equal to the mean stress, which follows from the use of virtual work with an isotropic virtual expansion, as noted above.

3.3 Uniaxial Stress

When we have a uniaxial stress the force flux density must vary with direction. In 2D let us consider a uniaxial stress \(\sigma\) in the x direction, corresponding to \(\theta =0\). The simplest force flux density distribution to choose is

$$\begin{aligned} S\left( \theta \right) =\frac{\sigma }{2}\left( 4\cos ^2\theta -1\right) \mathrm {\quad in \; 2 \; dimensions.} \end{aligned}$$
(21)

This satisfies \(S\left( \theta \right) =S\left( \pi +\theta \right)\), which is a requirement since each fibre points in two opposite directions. In addition, the mean force flux density is

$$\begin{aligned} \frac{1}{\pi }\int _0^\pi S\left( \theta \right) d\theta= & {} \ \frac{1}{\pi }\int _0^\pi \frac{\sigma }{2}\left( 4\cos ^2\theta -1\right) d\theta =\frac{\sigma }{2}\mathrm {,} \end{aligned}$$
(22)

corresponding to half the isotropic value and the stress in the x direction is

$$\begin{aligned} \frac{2}{\pi }\int _0^\pi S\left( \theta \right) \cos ^2\theta d\theta= & {} \ \frac{1}{\pi }\int _0^\pi \sigma \left( 4\cos ^2\theta -1\right) \cos ^2\theta d\theta \nonumber \\= & {} \ \frac{1}{\pi }\int _0^\pi \sigma \left( 3-4\sin ^2\theta \right) \cos ^2\theta d\theta \nonumber \\= & {} \ \frac{1}{\pi }\int _0^\pi \sigma \left( 3\cos ^2\theta -\sin ^2 2\theta \right) d\theta =\sigma \mathrm {,} \end{aligned}$$
(23)

as required. Eq. (21) tells us that \(S=\dfrac{3\sigma }{2}\) when \(\theta =0\) and \(S=-\dfrac{\sigma }{2}\) when \(\theta =\dfrac{\pi }{2}\). This means that if we treat the fibres as simply elastic bars the Poisson’s ratio is equal to \(\frac{1}{3}\) in two-dimensional plane stress.

We can repeat this process in 3D, now with a uniaxial stress in the z direction,

$$\begin{aligned} S\left( \phi \right) =\frac{\sigma }{2}\left( 5\cos ^2\phi -1\right) \mathrm {\quad in \; 3 \; dimensions} \end{aligned}$$
(24)

because then the mean force flux density,

$$\begin{aligned} \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } S\left( \phi \right) d\theta \sin \phi d\phi= & {} \ 3\int _0^\frac{\pi }{2} S\left( \phi \right) \sin \phi d\phi \nonumber \\= & {} \ \int _0^\frac{\pi }{2} \frac{3\sigma }{2}\left( 5\cos ^2\phi -1\right) \sin \phi d\phi \nonumber \\= & {} \ \left[ \frac{3\sigma }{2}\left( -\frac{5}{3}\cos ^3\phi +\cos \phi \right) \right] _0^\frac{\pi }{2}=\sigma \mathrm {,} \end{aligned}$$
(25)

corresponding to one third the isotropic value and the stress in the z direction is

$$\begin{aligned} \frac{3}{2\pi }\int _{\phi =0}^{\frac{\pi }{2}}\int _{\theta =0}^{2\pi } S\left( \phi \right) \cos ^2\phi d\theta \sin \phi d\phi= & {} \ \int _0^\frac{\pi }{2} \frac{3\sigma }{2}\left( 5\cos ^4\phi -\cos ^2\phi \right) \sin \phi d\phi \nonumber \\= & {} \ \left[ \frac{3\sigma }{2}\left( -\cos ^5\phi +\frac{1}{3}\cos ^3\phi \right) \right] _0^\frac{\pi }{2}=\sigma \mathrm {,} \end{aligned}$$
(26)

as required. Equation (24) tells us that \(S=2\sigma\) when \(\phi =0\) and \(S=-\dfrac{\sigma }{2}\) when \(\phi =\dfrac{\pi }{2}\). This means that if we treat the fibres as simply elastic bars the Poisson’s ratio is equal to \(\dfrac{1}{4}\) in 3D, as we would have expected [3].

3.4 General Stress State

We know that we can generate any stress state by superimposing the two or three orthogonal uniaxial principal stresses. Thus if \(\mathbf {q}\) is a unit vector we can generalise Eq. (21) to give

$$\begin{aligned} S\left( \mathbf {q}\right) = \frac{1}{2}\left( 4\mathbf {q}\cdot \varvec{\upsigma }\cdot \mathbf {q}-\mathrm {tr}\left( \varvec{\upsigma }\right) \right) \mathrm {\quad in \; 2 \; dimensions} \end{aligned}$$
(27)

and we can generalize Eq. (24) to give

$$\begin{aligned} S\left( \mathbf {q}\right) = \frac{1}{2}\left( 5\mathbf {q}\cdot \varvec{\upsigma }\cdot \mathbf {q}-\mathrm {tr}\left( \varvec{\upsigma }\right) \right) \mathrm {\quad in \; 3 \; dimensions} \end{aligned}$$
(28)

or, in general,

$$\begin{aligned} S\left( \mathbf {q}\right) = \frac{1}{2}\left( \left( N+2\right) \mathbf {q}\cdot \varvec{\upsigma }\cdot \mathbf {q}-\mathrm {tr}\left( \varvec{\upsigma }\right) \right) \mathrm {,} \end{aligned}$$
(29)

where again \(N=2\) or \(N=3\) is the number of dimensions. If we write

$$\begin{aligned} \bar{\sigma }=\frac{\mathrm {tr}\left( \varvec{\upsigma }\right) }{N}\mathrm {,} \end{aligned}$$
(30)

for the mean stress and

$$\begin{aligned} \varvec{\uptau }= \varvec{\upsigma }- \bar{\sigma }\;\mathbf {I}\mathrm {,} \end{aligned}$$
(31)

for the deviatoric stress, then

$$\begin{aligned} S\left( \mathbf {q}\right) = \frac{\left( N+2\right) }{2}\mathbf {q}\cdot \varvec{\uptau }\cdot \mathbf {q}+\bar{\sigma }\mathrm {.} \end{aligned}$$
(32)

\(\mathbf {I}\) is the unit tensor,

$$\begin{aligned} \mathbf {I}=\mathbf {ii}+\mathbf {jj}+\mathbf {kk}\mathrm {,} \end{aligned}$$
(33)

in 3 dimensions and in 2 dimensions we lose the \(\mathbf {kk}\) term. Note that

$$\begin{aligned} S\left( - \mathbf {q}\right) = S\left( \mathbf {q}\right) \mathrm {,} \end{aligned}$$
(34)

as we would expect.

Combining Eq. (32) with Eq. (14), we have the tension in the fibres in the direction of \(\mathbf {q}\),

$$\begin{aligned} T=\frac{N}{\left( N-1\right) \pi L}\left( \frac{\left( N+2\right) }{2}\mathbf {q}\cdot \varvec{\uptau }\cdot \mathbf {q}+\bar{\sigma }\right) \mathrm {.} \end{aligned}$$
(35)

4 Calculation of Equivalent Peridynamic Inter-Particle Arm Tensions

We can modify Eq. (35) to find the tensions in arms joining particles for SPH or peridynamics, thus introducing criteria 3 and 4 that were introduced in Section 2. We can write the tension in the arm joining particles a and b as

$$\begin{aligned} T_{ab}= & {} \ \frac{\omega _{ab}NS\left( \mathbf {q}_{ab}\right) }{\left( N-1\right) \pi L} \nonumber \\= & {} \ \frac{\omega _{ab}N}{\left( N-1\right) \pi L}\left( \frac{\left( N+2\right) }{2}\mathbf {q}_{ab}\cdot \varvec{\uptau }\cdot \mathbf {q}_{ab}+\bar{\sigma }\right) \mathrm {,} \end{aligned}$$
(36)

where \(\omega _{ab}\) is a non-dimensional weighting function which will depend upon the length of the arm and the size of the particles a and b. Again, \(\varvec{\uptau }\) is the deviatoric stress and \(\bar{\sigma }\) is the mean stress.

$$\begin{aligned} \mathbf {q}_{ab} = \frac{\mathbf {r}_b-\mathbf {r}_a}{r_{ab}} = -\mathbf {q}_{ba}\mathrm {,} \end{aligned}$$
(37)

is the unit vector from a to b. Particle a is currently located at \(\mathbf {r}_a\) and

$$\begin{aligned} r_{ab}=\left| \mathbf {r}_a-\mathbf {r}_b\right| \mathrm {,} \end{aligned}$$
(38)

is the actual length of the arm. The weighted length of the arm is,

$$\begin{aligned} R_{ab}=\omega _{ab}r_{ab}\mathrm {,} \end{aligned}$$
(39)

and L is now the total weighted length of the arms per unit area or unit volume,

$$\begin{aligned} L=\sum R_{ab}\mathrm {,\;per\;unit\;area\;or\;volume.} \end{aligned}$$
(40)

If we multiply all the weightings by the same constant, it makes no difference to \(T_{ab}\) since \(T_{ab}\) depends upon the ratio \(\dfrac{\omega _{ab}}{L}\).

4.1 Choice of Arm Length Weighting Function

There is no ‘correct’ arm weighting function since any weighting function should in principal be able to model a constant stress. However some functions will work better than others when it comes to numerical work. In choosing a weighting function, we want to be able to estimate the the value of L from Eq. (40) by replacing the summation by an integral and we want to be able to produce an equation for \(T_{ab}\) which is consistent with the results from conventional SPH and peridynamics.

Let us assume we have a large number of randomly but evenly distributed particles of variable mass. The mass of particle a is \(m_a\). The average density is \(\rho\) with the units of mass per unit area in 2D and mass per unit volume in 3D.

Fig. 3
figure 3

A typical kernel, \(W\left( \dfrac{r_{ab}}{h_a},h_a\right) \propto \left( 1-\dfrac{r_{ab}^2}{h_a^2}\right) ^5\) and its derivative, \(\dfrac{\partial W}{\partial r_{ab}}\)

Full size image

We will will write the weighting of the arm ab as

$$\begin{aligned} \omega _{ab}=\frac{R_{ab}}{r_{ab}}=-\frac{m_a m_b}{C^{\left( N-1\right) }\rho ^2} \left( \frac{\partial }{\partial r_{ab}}W\left( \frac{r_{ab}}{h_a},h_a\right) +\frac{\partial }{\partial r_{ab}}W\left( \frac{r_{ab}}{h_b},h_b\right) \right) \mathrm {,} \end{aligned}$$
(41)

where C is a constant with the units of length and \(N=2\) or \(N=3\) is the number of dimensions. As noted above the value of C does not influence \(T_{ab}\), but we have included it to make Eq. (41) non-dimensional.

We have chosen this rather complicated expression for \(\omega _{ab}\) because we shall see that \(W\left( \dfrac{r_{ab}}{h_b},h_b\right)\) is the ‘kernel’ used in SPH. Our \(W\left( \dfrac{\left| \mathbf {r}-\mathbf {r}_b\right| }{h_b},h_b\right)\) is exactly equivalent to \(W\left( \mathbf {r}-\mathbf {r}_b,h\right)\) in Monaghan’s 1992 paper [13], except we assume that the ‘size’ of the particle b as represented by \(h_b\) may vary from particle to particle.

Equation (38) of Ganzenmüller et al. [11], in which their \(X_{ij}\) is our \(r_{ab}\), relates \(W\left( \right)\) to the function \(\underline{\omega }\left\langle \varvec{\xi }\right\rangle\) used in peridynamics [8].

\(W\left( \dfrac{r_{ab}}{h_b},h_b\right)\) depends upon \(r_{ab}\) and upon \(h_b\) and it is largest when \(r_{ab}=0\) and decays reaching zero when \(\dfrac{r_{ab}}{h_b}\) reaches a certain constant value, which may not be 1.0 depending upon how we define \(h_b\). Thus \(\dfrac{\partial }{\partial r_{ab}}W\left( \dfrac{r_{ab}}{h_a},h_a\right)\) is negative and \(R_{ab}\) is positive, as we would expect.

Figure 3 shows a typical kernel, and note that the length \(r_{ab}\) is always taken as positive.

Clearly particles of larger mass should have a larger dimension, so we could write

$$\begin{aligned} h_b= & {} \ \left( \frac{m_b}{\pi \rho }\right) ^{\frac{1}{2}},\mathrm {\quad in \; 2 \; dimensions},\end{aligned}$$
(42)
$$\begin{aligned} h_b= & {} \ \left( \frac{3m_b}{4\pi \rho }\right) ^{\frac{1}{3}},\mathrm {\quad in \; 3 \; dimensions},\end{aligned}$$
(43)
$$\begin{aligned} h_b= & {} \ \left( \frac{Nm_b}{2\left( N-1\right) \pi \rho }\right) ^{\frac{1}{N}},\mathrm {\quad in \; }N \mathrm {\; dimensions}\mathrm {.} \end{aligned}$$
(44)

If we do this \(\dfrac{r_{ab}}{h_b}\) will almost certainly not be equal to 1.0 where the kernel becomes equal to 0.

W is a scalar function and in writing \(W\left( \dfrac{\left| \mathbf {r}-\mathbf {r}_a\right| }{h_b},h_b\right)\) we are assuming that W is radially symmetric and depends only on the ratio \(\dfrac{\left| \mathbf {r}-\mathbf {r}_a\right| }{h_b}\) and \(h_b\). It is possible to have kernels which are not radially symmetric, but that would require additional information, for example a symmetric second order tensor to define the dimensions and orientations of the axes of an ellipsoid. Following Monaghan [13] will write

$$\begin{aligned} W_{ba}=W\left( \frac{r_{ab}}{h_b},h_b\right) \mathrm {,} \end{aligned}$$
(45)

but now because \(h_a\) and \(h_b\) may be different

$$\begin{aligned} W_{ab}=W\left( \frac{r_{ab}}{h_a},h_a\right) \mathrm {,} \end{aligned}$$
(46)

may not be equal to \(W_{ba}\). To remember which is which

$$\begin{aligned} W_{ba} = W_{b\mathrm {\;at\;}a}, \end{aligned}$$
(47)

is the weighting of particle b at particle a. In 3D, the kernel has the property

$$\begin{aligned} \int W\left( \frac{r_b}{h_b},h_b\right) dV=1\mathrm {,} \end{aligned}$$
(48)

where

$$\begin{aligned} r_b=\left| \mathbf {r}-\mathbf {r}_b\right| \mathrm {,} \end{aligned}$$
(49)

is the distance from particle b to a typical point \(\mathbf {r}\). Therefore

$$\begin{aligned} \int _0^\infty W\left( \frac{r_b}{h_b},h_b\right) 4\pi r_b^2dr_b=1\mathrm {,} \end{aligned}$$
(50)

in 3D. The upper limit of integration is taken as infinity, but in practice kernels will always be of finite size and be equal to zero beyond a certain horizon.

If we write

$$\begin{aligned} W\left( \frac{r_b}{h_b},h_b\right) = \frac{1}{h_b^3}f\left( \frac{r_b}{h_b}\right) \mathrm {,} \end{aligned}$$
(51)

then

$$\begin{aligned} \int _0^\infty \frac{1}{h_b^3}f\left( \frac{r_b}{h_b}\right) 4\pi r_b^2dr_b=\int _0^\infty \ f\left( u\right) 4\pi u^2du=1\mathrm {,} \end{aligned}$$
(52)

and we can use the same dimensionless function \(f\left( \right)\) for all particles, regardless of their size. The equivalent relationships in N dimensions are

$$\begin{aligned} W\left( \frac{r_b}{h_b},h_b\right) = \frac{1}{h_b^N}f\left( \frac{r_b}{h_b}\right) \mathrm {,} \end{aligned}$$
(53)

and

$$\begin{aligned} \int _0^\infty f\left( u\right) 2\left( N-1\right) \pi u^{\left( N-1\right) } du=1\mathrm {.} \end{aligned}$$
(54)

Eq. (41) can now be written

$$\begin{aligned} \omega _{ab}=-\frac{m_a m_b}{C^{\left( N-1\right) }\rho ^2}\left( \frac{1}{h_a^{\left( N+1\right) }}f'\left( \frac{r_{ab}}{h_a}\right) + \frac{1}{h_b^{\left( N+1\right) }}f'\left( \frac{r_{ab}}{h_b}\right) \right) \mathrm {,} \end{aligned}$$
(55)

where the non-dimensional function

$$\begin{aligned} f'\left( u\right) =\frac{d}{du}f\left( u\right) \mathrm {.} \end{aligned}$$
(56)

The reason for \(\dfrac{1}{h_b^{\left( N+1\right) }}\), rather than the \(\dfrac{1}{h_b^N}\) that one might have expected is that

$$\begin{aligned} \frac{\partial W_{ba}}{\partial r_{ab}} = \frac{\partial }{\partial r_{ab}}W\left( \frac{r_{ab}}{h_b},h_b\right) =\frac{\partial }{\partial r_{ab}}\left( \frac{1}{h_b^N}f\left( \frac{r_{ab}}{h_b}\right) \right) =\frac{1}{h_b^{\left( N+1\right) }}f'\left( \frac{r_{ab}}{h_b}\right) \mathrm {.} \end{aligned}$$
(57)

We can see that Eq. (55) is dimensionally consistent with the units of length on both sides.

4.2 Total Weighted Length of Arms Per Joining Particles

Let us associate only the first part of \(R_{ab}\) with particle a and the second part with b. If we add the contributions for all the particles to which a is connected we obtain the sum of the weighted lengths associated with a,

$$\begin{aligned} l_a=\sum _b R_{ab}=\sum _b\omega _{ab}r_{ab}=-\frac{m_a}{\rho C^{\left( N-1\right) }h_a^{\left( N+1\right) }}\sum _b \frac{m_b r_{ab}}{\rho }f'\left( \frac{r_{ab}}{h_a}\right) \mathrm {.} \end{aligned}$$
(58)

However \(\dfrac{m_b}{\rho }\) is an element of area in 2D or volume in 3D and if we assume that we have a large number of particles we can replace the summation by an integral to give

$$\begin{aligned} l_a= & {} \ -\frac{m_a}{\rho C^{\left( N-1\right) }h_a^{\left( N+1\right) }}\int _0^\infty rf'\left( \frac{r}{h_a}\right) 2\left( N-1\right) \pi r^{\left( N-1\right) }dr \nonumber \\= & {} \ -\frac{m_a}{\rho C^{\left( N-1\right) }}\int _0^\infty f'\left( u\right) 2\left( N-1\right) \pi u^Ndu \nonumber \\= & {} \ -\frac{m_a}{\rho C^{\left( N-1\right) }}\left[ \ f\left( u\right) 2\left( N-1\right) \pi u^N\right] _0^\infty \nonumber \\&+\frac{m_a}{\rho C^{\left( N-1\right) }}\int _0^\infty f\left( u\right) 2N\left( N-1\right) \pi u^{\left( N-1\right) }du \nonumber \\= & {} \ \frac{Nm_a}{\rho C^{\left( N-1\right) }}\mathrm {,} \end{aligned}$$
(59)

if we stipulate that \(f\left( u\right)\) is finite when \(u=0\). Thus

$$\begin{aligned} l_a= \frac{2m_a}{\rho C}\mathrm {,\quad in \; 2 \; dimensions,} \end{aligned}$$
(60)

and

$$\begin{aligned} l_a= \frac{3m_a}{\rho C^2}\mathrm {,\quad in \; 3 \; dimensions.} \end{aligned}$$
(61)

This is the total weighted length associated with particle a and to find the total weighted length per unit area or per unit volume as appropriate we need to multiply by \(\dfrac{\rho }{m_a}\) to give

$$\begin{aligned} L= \frac{N}{C^{\left( N-1\right) }}\mathrm {.} \end{aligned}$$
(62)

Thus, finally,

$$\begin{aligned} \frac{N\omega _{ab}}{L}=-\frac{m_a m_b}{\rho ^2}\left( \frac{\partial W_{ab}}{\partial r_{ab}} + \frac{\partial W_{ba}}{\partial r_{ab}}\right) \mathrm {,} \end{aligned}$$
(63)

which is independent of whatever value we have chosen for the constant length C.

5 Arm Tensions

5.1 Constant Stress and Density

The formula for the tension in the arm ab is given by Eq. (36) and upon substituting in Eq. (63),

$$\begin{aligned} T_{ab} = - \frac{m_a m_b}{\rho ^2} \left( \frac{\partial W_{ab}}{\partial r_{ab}} + \frac{\partial W_{ba}}{\partial r_{ab}} \right) S\left( \mathbf {q}_{ab}\right) \mathrm {.} \end{aligned}$$
(64)

Thus the total force applied to particle a divided by its mass is

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = \sum _b T_{ab}\mathbf {q}_{ab} = - \frac{1}{\rho ^2} \sum _b m_b \left( \frac{\partial W_{ab}}{\partial r_{ab}} + \frac{\partial W_{ba}}{\partial r_{ab}} \right) \mathbf {q}_{ab}S\left( \mathbf {q}_{ab}\right) \mathrm {.} \end{aligned}$$
(65)

Following Monaghan [13] we can write the gradient

$$\begin{aligned} \nabla _a W_{ab}&= \frac{\partial W_{ab}}{\partial \mathbf {r}_a} = \frac{\partial r_{ab}}{\partial \mathbf {r}_a} \frac{\partial W_{ab}}{\partial r_{ab}} = - \mathbf {q}_{ab} \frac{\partial W_{ab}}{\partial r_{ab}}\nonumber \\&= - \nabla _b W_{ab}\mathrm {,} \end{aligned}$$
(66)

so that

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = \sum _b T_{ab}\mathbf {q}_{ab} = \frac{1}{\rho ^2} \sum _b m_b \left( \nabla _a W_{ab} + \nabla _a W_{ba}\right) S\left( \mathbf {q}_{ab}\right) \mathrm {.} \end{aligned}$$
(67)

In the case of an hydrostatic pressure P then \(S=-P\) so that

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = \sum _b T_{ab}\mathbf {q}_{ab} = - \frac{1}{\rho ^2} \sum _b m_b \left( \nabla _a W_{ab} + \nabla _a W_{ba}\right) P\mathrm {.} \end{aligned}$$
(68)

5.2 Variable Stress and Density

In Eq. (67), we assumed constant stress and density. But in general the stress and density will vary, but slowly compared to the particle spacing. Let us write \(\rho _a\) for the density associated with particle a and \(S_a\left( \mathbf {q}_{ab}\right)\) for the force flux density associated with particle a in the direction of the unit vector \(\mathbf {q}_{ab}\). Remember that reversing the direction of \(\mathbf {q}\) does not change \(S\left( \mathbf {q}\right)\). So let us now write

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = \sum _b m_b \left( \frac{S_a\left( \mathbf {q}_{ab}\right) }{\rho _a^2}\nabla _a W_{ab} + \frac{S_b\left( \mathbf {q}_{ba}\right) }{\rho _b^2}\nabla _a W_{ba}\right) \mathrm {.} \end{aligned}$$
(69)

The corresponding arm tension would be

$$\begin{aligned} T_{ab} = - m_a m_b \left( \frac{S_a\left( \mathbf {q}_{ab}\right) }{\rho _a^2}\frac{\partial W_{ab}}{\partial r_{ab}} + \frac{S_b\left( \mathbf {q}_{ba}\right) }{\rho _b^2}\frac{\partial W_{ba}}{\partial r_{ab}} \right) \mathrm {.} \end{aligned}$$
(70)

In the case of isotropic pressure \(P_a\) at a and \(P_b\) at b,

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = -\sum _b m_b \left( \frac{P_a}{\rho _a^2}\nabla _a W_{ab} + \frac{P_b}{\rho _b^2}\nabla _a W_{ba}\right) \mathrm {.} \end{aligned}$$
(71)

Finally, if all the particles have the same size, so that \(h_a=h_b\), and therefore ignoring any influence of how variable density modifies the size of particles, then \(W_{ab}=W_{ba}\) producing

$$\begin{aligned} \frac{\mathbf {f}_a}{m_a} = -\sum _b m_b \left( \frac{P_a}{\rho _a^2} + \frac{P_b}{\rho _b^2}\right) \nabla _a W_{ab} \mathrm {.} \end{aligned}$$
(72)

This is identical to Equation (3.3) of Monaghan [13].

6 Constitutive Relationships

6.1 Linear Elasticity

Let us assume that the fibres are linear elastic and we know the strain tensor \(\varvec{\upepsilon }\), which is assumed to be small from the unloaded state. The mean strain,

$$\begin{aligned} \bar{\epsilon }=\frac{\mathrm {tr}\left( \varvec{\upepsilon }\right) }{N}\mathrm {,} \end{aligned}$$
(73)

and the deviatoric strain,

$$\begin{aligned} \varvec{\upgamma }= \varvec{\upepsilon }- \bar{\epsilon }\;\mathbf {I}\mathrm {.} \end{aligned}$$
(74)

Substituting

$$\begin{aligned} \varvec{\uptau }=2G\varvec{\upgamma }\mathrm {,} \end{aligned}$$
(75)

and

$$\begin{aligned} \bar{\sigma }=NK\bar{\epsilon }\mathrm {,} \end{aligned}$$
(76)

into Eq. (32) we obtain

$$\begin{aligned} S\left( \mathbf {q}\right)= & {} \ \frac{2G\left( N+2\right) }{2}\mathbf {q}\cdot \varvec{\upgamma }\cdot \mathbf {q}+NK\bar{\epsilon } \nonumber \\= & {} \ G\left( N+2\right) \mathbf {q}\cdot \varvec{\upepsilon }\cdot \mathbf {q} +\left( NK-G\left( N+2\right) \right) \bar{\epsilon } \mathrm {,} \end{aligned}$$
(77)

where G is the shear modulus of the equivalent isotropic continuum and the 2 is there because the shear modulus is defined in terms of the ‘engineering’ shear strain rather than the ‘mathematical’ shear strain. K is the bulk modulus and it appears as NK because K is defined using the volumetric strain, which is \(N\bar{\epsilon }\) in N dimensions. In terms of Young’s modulus E and Poisson’s ratio \(\nu\),

$$\begin{aligned} G=\frac{E}{2\left( 1+\nu \right) }\mathrm {.} \end{aligned}$$
(78)

In 3D,

$$\begin{aligned} K=\frac{E}{3\left( 1-2\nu \right) }\mathrm {,} \end{aligned}$$
(79)

for two-dimensional plane stress,

$$\begin{aligned} K=\frac{E}{2\left( 1-\nu \right) }\mathrm {,} \end{aligned}$$
(80)

and for two-dimensional plane strain, in which the strain perpendicular to the plane is zero,

$$\begin{aligned} K=\frac{E}{2\left( 1-2\nu \right) \left( 1+\nu \right) }\mathrm {.} \end{aligned}$$
(81)

In 3D the elastic constant appearing in Eq. (77),

$$\begin{aligned} NK-G\left( N+2\right)= & {} \ \frac{3E}{3(1-2\nu )} - \frac{5E}{2(1+\nu )} \nonumber \\= & {} \ \frac{E\left( 2(1+\nu )-5(1-2\nu )\right) }{2(1+\nu )(1-2\nu )}\mathrm {,} \end{aligned}$$
(82)

which is zero when \(\nu =\frac{1}{4}\), as expected from the above. Similarly for plane stress

$$\begin{aligned} NK-G(N+2)= & {} \ \frac{2E}{2(1-\nu )} - \frac{4E}{2(1+\nu )} \nonumber \\= & {} \ \frac{E\left( (1+\nu )-2(1-\nu )\right) }{(1+\nu )(1-\nu )}\mathrm {,} \end{aligned}$$
(83)

which is zero when \(\nu =\frac{1}{3}\), again as expected. For plane strain,

$$\begin{aligned} NK-G\left( N+2\right)= & {} \ \frac{2E}{2\left( 1-2\nu \right) \left( 1+\nu \right) } - \frac{4E}{2\left( 1+\nu \right) } \nonumber \\= & {} \ \frac{E\left( 1-2\left( 1-2\nu \right) \right) }{\left( 1-2\nu \right) \left( 1+\nu \right) }\mathrm {,} \end{aligned}$$
(84)

which is zero when \(\nu =\frac{1}{4}\), as was the case in 3D. Thus we can control the Poisson’s ratio by including the effect of \(\bar{\epsilon }\) upon the arm tensions, in exactly the same way as described in Section 15 of Silling’s 2000 paper [3].

6.2 Newtonian Fluid

If we replace the strain \(\varvec{\upepsilon }\) by the strain rate \(\dot{\varvec{\upepsilon }}\), the shear modulus G by the viscosity \(\mu\) and the bulk modulus K by the bulk viscosity \(\kappa\) in the elastic Eq. (77), and include the thermodynamic pressure P then we obtain

$$\begin{aligned} S\left( \mathbf {q}\right) = -P + \mu \left( N+2\right) \mathbf {q}\cdot \dot{\varvec{\upepsilon }}\cdot \mathbf {q} +\left( N\kappa -\mu \left( N+2\right) \right) \bar{\dot{\epsilon }}\mathrm {,} \end{aligned}$$
(85)

where N is again the number of dimensions. If

$$\begin{aligned} \mathbf {v}_a=\frac{d\mathbf {r}_a}{dt}\mathrm {,} \end{aligned}$$
(86)

is the velocity of particle a, then for the particle pair a and b

$$\begin{aligned} \dot{\epsilon }_{ab}= \mathbf {q}_{ab}\cdot \dot{\varvec{\upepsilon }}\cdot \mathbf {q}_{ab} = \frac{ \left( \mathbf {v}_a -\mathbf {v}_b\right) \cdot \left( \mathbf {r}_a -\mathbf {r}_b\right) }{r_{ab}^2}\mathrm {,} \end{aligned}$$
(87)

is equal to the rate of strain in the arm. This appears in equation (4.2) of Monaghan [13]. Clearly one has to be careful if \(r_{ab}\) happens to be very small, but \(\dfrac{\partial W_{ab}}{\partial r_{ab}}\) should tend to zero as \(r_{ab}\rightarrow 0\), meaning that the force is finite. Even so Monaghan includes the factor \(\eta ^2\) in the denominator in his equation (4.2). An alternative would be to use a kernel with a flat top so that it has zero curvature at \(r_{ab}=0\).

7 An Elastic–Plastic Material

It is relatively easy to model an elastic solid or viscous fluid with arm tensions. However, it is not easily possible to model a material with a given yield criterion such as the well-known Tresca and von Mises criteria or the recently introduced Bigoni and Andrea Piccolroaz criterion [20]. On the other hand it is easy to specify a yield condition in terms of peridynamic arm tensions and compressions, and then see what this means in terms of stress and a yield criterion.

Let us imagine that the tension in an arm depends on

  1. 1.

    the volumetric strain of the particles at its ends which produces an elastic isotropic stress via the bulk modulus and

  2. 2.

    an elastic-perfectly plastic elongation of the arm acting on its own.

The arms will not all begin to yield at the same time so that the transition from elastic to plastic will be gradual. However, let us assume that all the arms connected to a particle are yielding, either in tension or compression, such that the principal plastic strain increments are \(d\epsilon _{\mathrm {plastic\;I}}\), \(d\epsilon _{\mathrm {plastic\;II}}\) and \(d\epsilon _{\mathrm {plastic\;III}}\) in 3D satisfy

$$\begin{aligned} d\epsilon _{\mathrm {plastic\;I}}+d\epsilon _{\mathrm {plastic\;II}}+d\epsilon _{\mathrm {plastic\;III}}=0 \mathrm {,} \end{aligned}$$
(88)

so that the plastic volumetric strain is zero. We can impose this requirement simply via the elastic isotropic stress. If we align the principal strain increments with the coordinate axes, we have the tensor

$$\begin{aligned} d\varvec{\upepsilon }_{\mathrm {plastic}} =d\epsilon _{\mathrm {plastic\;I}}\mathbf {ii} +d\epsilon _{\mathrm {plastic\;II}}\mathbf {jj} +d\epsilon _{\mathrm {plastic\;III}}\mathbf {kk}\mathrm {,} \end{aligned}$$
(89)

so that, in the direction of the unit vector

$$\begin{aligned} \sin \phi \left( \cos \theta \mathbf {i}+\sin \theta \mathbf {j}\right) +\cos \phi \mathbf {k}\mathrm {,} \end{aligned}$$

the strain increment is

$$\begin{aligned} d\epsilon _{\mathrm {plastic}}= & {} \ \sin ^2\phi \left( \cos ^2\theta d\epsilon _{\mathrm {plastic\;I}}+\sin ^2\theta d\epsilon _{\mathrm {plastic\;II}}\right) +\cos ^2\phi d\epsilon _{\mathrm {plastic\;III}} \nonumber \\= & {} \ \sin ^2\phi \left( \cos ^2\theta d\epsilon _{\mathrm {plastic\;I}}+\sin ^2\theta d\epsilon _{\mathrm {plastic\;II}}\right) \nonumber \\&-\cos ^2\phi \left( d\epsilon _{\mathrm {plastic\;I}}+d\epsilon _{\mathrm {plastic\;II}}\right) \mathrm {,} \end{aligned}$$
(90)

which is positive if the arm is yielding in tension and negative if it is yielding in compression. The boundary between the tension and compression zones is where

$$\begin{aligned} \tan ^2\phi _{\mathrm {boundary}}=\frac{\left( d\epsilon _{\mathrm {plastic\;I}}+d\epsilon _{\mathrm {plastic\;II}}\right) }{\left( \cos ^2\theta d\epsilon _{\mathrm {plastic\;I}}+\sin ^2\theta d\epsilon _{\mathrm {plastic\;II}}\right) }\mathrm {.} \end{aligned}$$
(91)

For simplicity, let us assume that all the arms have the same yield strength, either in tension or compression so that the force flux density is equal to \(\pm S_{\mathrm {y}}\) per unit solid angle where the constant \(\pm S_{\mathrm {y}}\) is the yield value of S. The principal stresses are aligned with the principal strain increments and therefore, ignoring the isotropic stress from the elastic bulk modulus,

$$\begin{aligned} \sigma _{\mathrm {I}}= & {} \ \frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =0}^{2\pi }\int _{\phi =0}^{\phi _{\mathrm {boundary}}}\left( 1-\cos ^2\phi \right) \sin \phi \,d\phi \cos ^2\theta \,d\theta \nonumber \\&- \frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =0}^{2\pi }\int _{\phi =\phi _{\mathrm {boundary}}}^{\frac{\pi }{2}}\left( 1-\cos ^2\phi \right) \sin \phi \,d\phi \cos ^2\theta \,d\theta \nonumber \\= & {} \ S_{\mathrm {y}}-\frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\left( 3\cos \phi _{\mathrm {boundary}}-\cos ^3\phi _{\mathrm {boundary}}\right) \cos ^2\theta \,d\theta \mathrm {,} \end{aligned}$$
(92)
$$\begin{aligned} \sigma _{\mathrm {II}}=S_{\mathrm {y}}-\frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\left( 3\cos \phi _{\mathrm {boundary}}-\cos ^3\phi _{\mathrm {boundary}}\right) \sin ^2\theta \,d\theta \mathrm {,} \end{aligned}$$
(93)

and

$$\begin{aligned} \sigma _{\mathrm {III}}= & {} \ \frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =0}^{2\pi }\int _{\phi =0}^{\phi _{\mathrm {boundary}}}\cos ^2\phi \sin \phi \,d\phi \,d\theta \nonumber \\&- \frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =0}^{2\pi }\int _{\phi =\phi _{\mathrm {boundary}}}^{\frac{\pi }{2}}\cos ^2\phi \sin \phi \,d\phi \,d\theta \nonumber \\= & {} \ S_{\mathrm {y}} -\frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\cos ^3\phi _{\mathrm {boundary}} \,d\theta \mathrm {.} \end{aligned}$$
(94)

Thus, the deviatoric principal stresses are

$$\begin{aligned} \tau _{\mathrm {I}}= & {} \ \frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\cos \phi _{\mathrm {boundary}} d\theta \nonumber \\&-\frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\left( 3\cos \phi _{\mathrm {boundary}}-\cos ^3\phi _{\mathrm {boundary}}\right) \cos ^2\theta \,d\theta \nonumber \\ \tau _{\mathrm {II}}= & {} \ \frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\cos \phi _{\mathrm {boundary}} \,d\theta \nonumber \\&-\frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\left( 3\cos \phi _{\mathrm {boundary}}-\cos ^3\phi _{\mathrm {boundary}}\right) \sin ^2\theta \,d\theta \nonumber \\ \tau _{\mathrm {III}}= & {} \ \frac{S_{\mathrm {y}}}{\pi }\int _{\theta =0}^{2\pi }\left( \cos \phi _{\mathrm {boundary}}-\cos ^3\phi _{\mathrm {boundary}}\right) \,d\theta \mathrm {.} \end{aligned}$$
(95)

These equations will probably have to be integrated numerically and this has been done to plot the yield surface on the \(\pi\) -plane [21] in Fig. 4. The arrows indicate the corresponding plastic strain increments, and it can be seen that they are normal to the surface and so obey the normality condition, as one would expect. Fig. 5 shows the regions on the sphere yielding in tension and compression.

Fig. 4
figure 4

\(\pi\) plane showing the yield surface in cross section and the plastic strain increment vectors normal to the surface

Full size image
Fig. 5
figure 5

White zones yielding in tension, blue in compression. Left simple tension, right pure shear, middle somewhere between

Full size image

However, we can perform the integration for the two simple special cases. For the case of simple tension or compression,

$$\begin{aligned} d\epsilon _{\mathrm {plastic\;I}}= & {} \ d\epsilon _{\mathrm {plastic\;II}}=-\frac{1}{2}d\epsilon _{\mathrm {plastic\;III}}\mathrm {,} \nonumber \\ \tan ^2\phi _{\mathrm {boundary}}= & {} \ 2 \mathrm {,} \end{aligned}$$
(96)

to give

$$\begin{aligned} \tau _{\mathrm {I}}= & {} \ \tau _{\mathrm {II}} =-\frac{2S_{\mathrm {y}}}{3\sqrt{3}}\mathrm {,} \nonumber \\ \tau _{\mathrm {III}}= & {} \ \frac{4S_{\mathrm {y}}}{3\sqrt{3}}\mathrm {.} \end{aligned}$$
(97)

Thus

$$\begin{aligned} \sigma _{\mathrm {yield\;tension}}=\tau _{\mathrm {III}}-\tau _{\mathrm {I}}=\frac{2S_{\mathrm {y}}}{\sqrt{3}}\mathrm {.} \end{aligned}$$
(98)

For the case of pure shear,

$$\begin{aligned} d\epsilon _{\mathrm {plastic\;III}}= & {} \ 0\mathrm {,} \nonumber \\ d\epsilon _{\mathrm {plastic\;II}}= & {} \ -d\epsilon _{\mathrm {plastic\;I}}\mathrm {,} \nonumber \\ \sin ^2\phi _{\mathrm {boundary}}\left( \cos ^2\theta -\sin ^2\theta \right)= & {} \ 0\mathrm {,} \end{aligned}$$
(99)

which means that the tension and compression zones are separated by planes at \(\theta =\pm \frac{\pi }{4}\) to give

$$\begin{aligned} \tau _{\mathrm {I}}=-\tau _{\mathrm {II}}= & {} \ 2\frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =-\frac{\pi }{4}}^{\frac{\pi }{4}}\int _{\phi =0}^\frac{\pi }{2}\left( 1-\cos ^2\phi \right) \sin \phi \,d\phi \cos ^2\theta \,d\theta \nonumber \\&-2\frac{3S_{\mathrm {y}}}{2\pi }\int _{\theta =\frac{\pi }{4}}^{\frac{3\pi }{4}}\int _{\phi =0}^\frac{\pi }{2}\left( 1-\cos ^2\phi \right) \sin \phi \,d\phi \cos ^2\theta \,d\theta \nonumber \\= & {} \ \frac{2S_{\mathrm {y}}}{\pi }\mathrm {,} \nonumber \\ \tau _{\mathrm {III}}= & \ 0\mathrm {.} \end{aligned}$$
(100)

Thus

$$\begin{aligned} \sigma _{\mathrm {yield\;shear}}=\tau _{\mathrm {I}}=\frac{2S_{\mathrm {y}}}{\pi }\mathrm {,} \end{aligned}$$
(101)

so that

$$\begin{aligned} \frac{\sigma _{\mathrm {yield\;tension}}}{\sigma _{\mathrm {yield\;shear}}}=\frac{\pi }{\sqrt{3}}=1.814\mathrm {,} \end{aligned}$$
(102)

which lies between the value of 2 from the Tresca yields criterion and \(\sqrt{3}=1.732\) from the von Mises yield criterion.

8 Fracture Mechanics

Dimensional analysis tells us that no amount of adjustment of stress/strain relationships will enable us to model brittle fracture because it is not possible to produce a dimensionless group containing the crack length. The Griffith theory [1, 2, 22] uses the concept of surface energy, that is the work required to increase the area of a crack with units of J/m\(^2\). Surface energy is conventionally given the symbol \(\gamma\), which should not be confused with the deviatoric strain \(\varvec{\upgamma }\) or its components. Youngs modulus E and the failure stress away from the crack, \(\sigma _{\mathrm {failure}}\) have units of N/m\(^2\). Thus if c is the length of an edge crack in a material (not to be confused with the micromodulus in Section 1), the only independent non-dimensional groups are

$$\begin{aligned} \frac{\sigma _{\mathrm {failure}}}{E}\mathrm {\quad and\quad }\frac{\gamma }{cE}\mathrm {.} \end{aligned}$$

Griffith used interchange of elastic and surface energy to show that

$$\begin{aligned} \frac{\sigma _{\mathrm {failure}}}{E} \approx \sqrt{\frac{2\gamma }{cE\pi }}\mathrm {,} \end{aligned}$$
(103)

so that

$$\begin{aligned} \sigma _{\mathrm {failure}}\approx \sqrt{\frac{\mathrm{2} E \gamma }{c \pi }}. \end{aligned}$$
(104)

However we do not need to postulate the relationship between surface energy and failure stress, we only need to be able to model surface energy. If we assume arm tensions are controlled by yield, then we need to specify an elongation to failure to give the surface energy. The corresponding strain in an arm will depend upon its length, with shorter arms needing higher strains.

This is familiar from necking in a tensile test on a ductile metal where the failure strain depends upon the gauge length since all the elongation is in the neck region. Thus effectively we are imagining that the arms fail by necking.

Let us write the surface energy as

$$\begin{aligned} \gamma = \delta \sigma _{\mathrm {yield\;tension}}\mathrm {,} \end{aligned}$$
(105)

where \(\delta\) is a constant length which is related to the amount of deformation associated with the surface energy. Then

$$\begin{aligned} \sigma _{\mathrm {failure}}\approx \sqrt{\frac{2\delta }{c \pi }}\sqrt{E\sigma _{\mathrm {yield}} / {\mathrm{tension}}}. \end{aligned}$$
(106)

Eq. (105) should be compared with the concept of the modulus of cohesion in Barenblatt [22]. Writing

$$\begin{aligned} \sigma _{\mathrm{yield}} / {\mathrm{tension}} = E {\epsilon}_{\mathrm{yield}} / {\mathrm{tension}}, \end{aligned}$$
(107)

where \(\epsilon _{\mathrm {yield\;tension}}\) is the yield strain or proof strain,

$$\begin{aligned} \sigma _{\mathrm {failure}}\approx \zeta \sigma _{\mathrm{yield}}/{\mathrm{tension}}, \end{aligned}$$
(108)

where the non-dimensional quantity

$$\begin{aligned} \zeta =\sqrt{\frac{2\delta }{c\pi \epsilon _{\mathrm{yield}}/{\mathrm{tension}}}}. \end{aligned}$$
(109)

Thus we can focus our attention on \(\zeta\) which will be less than 1 in any situation involving brittle fracture. If \(\zeta =1\) and \(\epsilon _{\mathrm {yield}}/{\mathrm{tension}} = \dfrac{1}{500}\), then \(\dfrac{\delta }{c}=\dfrac{\pi }{1000}\), which gives an indication of the sort of elongation we require of the inter-particle arms.

9 Numerical Simulation of Brittle Fracture

Let us replace the constitutive equation for linear elasticity in Eq. (77) by

$$\begin{aligned} S_a\left( \mathbf {q}_{ab}\right) = G\left( N+2\right) \left( \epsilon _{ab}-\epsilon _{ab}^{\mathrm {plastic}}\right) +\left( NK-G\left( N+2\right) \right) \bar{\epsilon }_a \mathrm {,} \end{aligned}$$
(110)

where \(\epsilon _{ab}\) is the total engineering strain calculated using Pythagoras’ theorem to give the current arm length from which we subtract the initial length and then divide by the initial length. \(\epsilon _{ab}^{\mathrm {plastic}}\) is the plastic strain. We will continue to calculate \(\bar{\epsilon }_a\) from \(\epsilon _{ab}\) so that the plastic volumetric strain is zero.

We now use the algorithm

$$\begin{aligned} \left. \begin{array}{ll} \epsilon _{ab}^{\mathrm {plastic}} = \epsilon _{ab}-\epsilon _{\mathrm {yield}} \mathrm {,} &{}\mathrm {if, }\epsilon _{ab}-\epsilon _{ab}^{\mathrm {plastic}} > +\epsilon _{\mathrm {yield}} \mathrm {,}\\ \\ \epsilon _{ab}^{\mathrm {plastic}} = \epsilon _{ab}+\epsilon _{\mathrm {yield}}\mathrm {,} &{}\mathrm {if, }\epsilon _{ab}-\epsilon _{ab}^{\mathrm {plastic}} <- \epsilon _{\mathrm {yield}}\mathrm {,}\\ \\ \mathrm {Otherwise} \ \epsilon _{ab}^{\mathrm{plastic} \ \mathrm{is} \ \mathrm{unchanged.}} \end{array} \right\} \end{aligned}$$
(111)

where \(\epsilon _{\mathrm {yield}}\) is the yield strain which is taken as positive.

10 Numerical Implementation

10.1 The Kernel

The choice of kernel \(W\left( \dfrac{r_b}{h_b},h_b\right)\) is arbitrary, provided that it satisfies Eq. (53) and Eq. (54), although some kernels will work better than others. We have chosen

$$\begin{aligned} f\left( u\right)= & {} \ \displaystyle \frac{\left( 1-\dfrac{u^2}{\alpha ^2}\right) ^k}{\displaystyle \int _0^\infty \left( 1-\dfrac{u^2}{\alpha ^2}\right) ^k2\left( N-1\right) \pi u^{\left( N-1\right) } du} \mathrm {,}\mathrm {\quad when\;}u\le \alpha \mathrm {,} \nonumber \\= & {} \ \ 0\mathrm {,}\mathrm {\quad when\;}u>\alpha \mathrm {,} \end{aligned}$$
(112)

to satisfy Eq. (54). The integer k and the non-dimensional constant \(\alpha\) are a matter of choice and are the same for all particles, regardless of their size. If \(k\rightarrow \infty\) and \(\alpha \rightarrow \infty\) we obtain the bell shaped Gaussian kernel. We have taken \(k=2\),

$$\begin{aligned} f\left( u\right)= & {} \ \displaystyle \frac{\left( 1-\dfrac{u^2}{\alpha ^2}\right) ^2}{2C \left( N-1\right) \pi \alpha ^N \left( \dfrac{1}{N}-\dfrac{2}{N+2}+\dfrac{1}{N+4}\right) } \mathrm {,} \mathrm {\quad when\;}u\le \alpha \mathrm {,} \nonumber \\= & {} \ \ 0\mathrm {\quad when\;}u>\alpha \mathrm {.} \end{aligned}$$
(113)

10.2 Model Setup

The numerical implementation that has been used to validate the theory is a simple elliptical disk in 2D with a crack spanning between the two focal points. The model is generated using elliptical coordinates for variables \(\xi \in (-\pi /2, \pi /2)\) and \(\eta \in (0, \pi )\) according to

$$\begin{aligned} x= & {} \ c \cosh (\xi ) \cos (\eta ), \nonumber \\ y= & {} \ c \sinh (\xi ) \sin (\eta ). \end{aligned}$$
(114)

The disk is stressed by an evenly distributed prescribed displacement at the boundary under the assumption of two-dimensional plane strain, which means no displacement in the z direction perpendicular to the \(x-y\) plane and displacements in the x and y directions which are independent of z.

Fig. 6
figure 6

The setup for the numerical example. The stress on the plate is introduced through an incrementally imposed displacement field on the particles at the perimeter (in the grey zones). The direction of the displacement is illustrated with the arrows

Full size image

This means that the strains \(\epsilon _z\), \(\gamma _{yz}\) and \(\gamma _{zx}\) are all zero, the stresses \(\tau _{yz}\) and \(\tau _{zx}\) are both zero, but \(\sigma _z\) is nonzero due to Poisson’s ratio effects in the elastic region. In the plastic region, stresses are larger than the yield stress can maintained since \(\sigma _z\) can adjust itself to limit the deviatoric stress.

The geometrical parameters that control the setup of the base geometry are shown in Tables 1 and 2, where \(n\eta\) refers to the number of divisions in the \(\eta\) direction and \(n\xi\) refers to the number of division in the \(\xi\) direction. The grid shown in Fig. 6 is used to define zones in which the particles are stored. The connectivity between the zones is computed and utilised every time when particle neighbour calculations are necessary. The setup of particles and arms follows a four-step process after the underlying grid has been generated. This is illustrated with the four quadrants a) - d) in Fig. 7. The first step is to populate all zones with constant number of particles, resulting in an increasing particle density closer to the focal point of the ellipse as a result of the parametrisation of Eq. (114). For the example that follows, each zone is populated with a pattern of 5x5 particles. A Monte Carlo inspired algorithm is then used to introduce noise in the particle distribution as shown in Fig. 7b and Fig. 7c, according to the procedure described in Fig. 8.

Fig. 7
figure 7

Showing the process of setting up the numerical model, starting from a regular particle distribution in a), in which noise is introduce using a Monte Carlo inspired algorithm as shown in b). Resulting particle distribution without the underlying grid of zones is shown in c) where some particles are highlighted for which the horizon (\(h_{a} \alpha\)) is drawn as circles. The last quadrant d) shows the resulting arms from connecting each particle with all the other particles within its horizon

Full size image

After the re-positioning of the particles, the particle-zone topology and the particle size need to be updated. The new size is calculated from,

$$\begin{aligned} h_a = \sum ^{n}_{b} \frac{|\mathbf {x}_{b} - \mathbf {x}_{a}|}{2 n}, \end{aligned}$$
(115)

where \(h_a\) is the particle size, \(\mathbf {x}_a\) are the coordinates of current particle, \(\mathbf {x}_b\) are the coordinates of a neighbouring particle, and n is the number of neighbours which is set to \(n = 5\). In a perfect even hexagonal-based circle packing, each circle has 6 adjacent neighbours. In a suboptimal case with noise and lower density packing it seemed reasonable to assume a lower number, thus the choice to set \(n = 5\).

From the particle size and the choice of kernel parameter \(\alpha\), the horizon for each particle a can be computed and the results for a few particles are illustrated in Fig. 7c. The horizon \(\mathcal {H}_{a}\) is the distance of connectivity and will be unique for each particle due to the irregularity of the distribution. Finally, the arms between the particles can be created by connecting each particle a with the neighbours withing its horizon \(\mathcal {H}_{a} = \alpha h_a\), as illustrated in Fig. 7d and Fig. 9. Note that the zone size should be chosen such that the shortest side of the zone is larger than the horizon of the largest particle within that zone.

Fig. 8
figure 8

Flowchart algorithm for the introduction of noise in an initially regular particle distribution, exemplified for a particle a with neighbours b. The particle size is updated only in each fifth iteration

Full size image
Table 1 Showing all the parameters that are used for setting up the underlying grid, the particle distribution and the material properties for the simulation
Full size table

In Table 1nP is the number of particles, nA is the number of arms, \(\alpha\) and k are constants that are used in the kernel Eq. (112) and Eq. (113), c is half the crack length which is specified in Eq. (114) and n is the number of neighbours used to calculate the particle size from Eq. (115). Furthermore, in Table 1\(\delta\) is the plastic elongation limit, E is the Young’s modulus, \(\epsilon _y\) is the yield strain, \(\sigma _y\) is the yield stress, \(\nu\) is the Poission’s ratio, \(\rho\) is the material density, G and K are the shear and bulk modulus calculated from Eq. (78) and Eq. (81), respectively.

Fig. 9
figure 9

All arms that connect neighbouring particles are shown in the left figure. The variation in density comes as a result of the varying particle size where particles are smaller closer to the two crack tips and larger towards the boundary. The largest particle has a radius which is more than 400 times greater that the smallest one. A zoomed in view of the sub region which is marked with a rectangle in the left figure and concentrated around the predefined crack as shown in the figure to the right

Full size image

10.3 Analytical Solution & Applied Load

The numerical implementation seeks to simulate progressive fracture and the results are compared to Griffith’s theory formulated in Eq. (103). The load that is applied to trigger fracture is a prescribed incremental displacement of the particles in the boundary zone. The elastic solution to the analytical equation as outlined in Eq. (116) is used to impose this prescribed displacement filed. The displacements are then converted to a boundary stress for comparison with Eq. (103). This is done by summing over the reaction forces of the particles in the boundary zone which results from the imposed displacements, and dividing that force with the area of the disk perimeter, where the thickness is set to 1.

The analytical solution is also used to study convergence of the elastic solution with increasing particle count as presented in Fig. 10. A derivation of the analytical solution is out of the scope of the paper but the interested reader is referred to p.(187 - 204) in [23]. For the case of plain strain, the analytical solution for the elliptical plate with an elliptical crack of zero width between the focal points can expressed in terms of a complex potential as

$$\begin{aligned} u - i v = \frac{S c}{4 G}(\sinh {\xi } \cos {\eta } - i \cosh {\xi } \sin {\eta })\left( 3 - 4 \nu - \frac{\sinh {\xi }^2 - \sin {\eta }^2}{\cosh {\xi }^2 - \cos {\eta }^2} \right) , \end{aligned}$$
(116)

where \(i=\sqrt{-1}\), u is the displacement in x-direction, v is the displacement in y-direction, \(\xi\) and \(\eta\) referrers to curvilinear coordinates as described in [23] pg.192 and our Eq. (114), G is the shear modulus for plain strain and \(\nu\) is the Poisson’s ratio of the material.

Fig. 10
figure 10

Showing a convergence study where the root mean square (RMS) for the displacement for the elastic solution of the theory presented here is compared with the analytical solution from Eq. (116). The numerical simulations are run for 5 different particle densities and compared to the analytical solution for the highest density (39200 particles)

Full size image

10.4 Fracture

In order to validate the fracture model the relationship between stress and surface energy was examined numerically and compared with with Griffith’s prediction, Eq. (103). It does not matter whether we have an edge crack or an internal crack, as we have studied, since we are primarily concerned with the fact that we expect the failure stress to be proportional to the square root of the surface energy divided by the crack length, and are less concerned with the constant of proportionality. Following the set up of the geometry as described above, the plastic elongation limit \(\delta\) was varied from c/500 to c/3250 with incremental steps of c/250. The dimensionless proportional relationship,

$$\begin{aligned} \frac{\sigma _{\mathrm {failure}}}{\sigma _{\mathrm {yield\;tension}}} \propto \sqrt{\frac{\delta }{c}}\mathrm {,} \end{aligned}$$
(117)

between the stress to failure over the yield stress and the square root of the elongation limit over half the crack width c, is expected to be linear.

In order to calculate particle damage \(\phi\) a damage number \(\mu\) at the level of the arm is introduced such that

$$\begin{aligned} \mu = \begin{cases} 0 &{} \text {if} \epsilon _{ab}^{\mathrm {plastic} }L_{ab} > \delta \mathrm {,}\\ 1 &{} \text {otherwise}\mathrm {.}\\ \end{cases} \end{aligned}$$
(118)

The particle damage is then computed from

$$\begin{aligned} \phi _a = \frac{\sum _{\mathcal {H}_{a}}\mu (\epsilon _{ab}^{\mathrm {plastic}}, \delta )}{n_b}\mathrm {,} \end{aligned}$$
(119)

where \(n_a\) is the number of arms within the horizon \(\mathcal {H}_{a}\) for particle a.

10.5 Results

The results from the simulations are first shown for the case when \(\delta = c/1000\) in Figs. 11 and 12, followed by a compilation of 11 simulations with varying \(\delta\). The load is increased by small increments until progressive fracture occurs such that the precise level of fracture stress could be obtained. The simulation is aborted when the crack propagation has reached a distance of 10c from the centre of the disk, effectively leaving the boundary zone intact. The elongation of the arms is shown in Fig. 11, where the total elongation in a) is computed from \((\epsilon _{ab}^{\mathrm {plastic}} + \epsilon _{ab}^{\mathrm {elastic}}) L_{ab}\) and the relation between the plastic elongation \(\epsilon _{ab}^{\mathrm {plastic}} L_{ab}\) and the plastic elongation limit \(\delta\) is shown in b). Figure 12 shows the particle damage in a) which is calculated from Eq. (119) and the total arm strain \(\epsilon _{ab}\) over the yield strain \(\epsilon _y\) in b).

Fig. 11
figure 11

Showing the total elongation of the arms a) and the plastic part of the elongation in the Figure in b). All arms including broken ones are drawn. A relative colour scheme is applied in a) where the most elongated arm is red and the least elongated arm in blue. The colour scheme in b) relates the plastic arm elongation to the elongation limit \(\delta\), where arms that exceed the elongation limit are coloured red

Full size image
Fig. 12
figure 12

Drawing the damage of the particles in a) with a colour scale form green to red where \(\phi \le 0.5\) is red and \(\phi = 1\) is green (no damaged arms). In b) the arm yield strain is drawn in a colour scheme where \(\epsilon _{ab} / \epsilon _y > 1\) is red and \(\epsilon _{ab} / \epsilon _y = 0\) is blue

Full size image
Fig. 13
figure 13

Showing \(\epsilon _{ab} / \epsilon _y\) for the arms as a result of different values for \(\delta\). \(\epsilon _{ab} / \epsilon _y > 1\) is red and \(\epsilon _{ab} / \epsilon _y = 0\) is blue. In the case of \(\delta = c/500\) the whole plate yields before fracture occurs

Full size image
Fig. 14
figure 14

Showing the relationship between LHS and RHS in Eq. (117). The dashed line is a least mean square approximation of the data. A linear relation is expected for correlation with Griffith’s theory

Full size image

The results of 11 simulations with a fixed irregular particle distribution and varying plastic elongation limit \(\delta\) can be seen in Figs. 13 and 14. Figure 14 shows the a comparison with the linear relationship predicted by the Griffith criterion. Note that one can only establish the slope of the graph, that is the constant in the Griffith criterion, by doing numerical experiments. The high values for the fracture stress in Fig. 14 are as a result of the plain strain assumption, as discussed above. The arm yield strain for the 11 simulations (including a 12th attempt for \(\delta = c/500\) where fracture did not occur as a limiting case) are shown in Fig. 13.

11 Conclusion

The separation of the influence of the fibre orientation and the length of fibres per unit volume from the arm length between particles simplifies the peridynamic theory. It enables us to simulate a homogeneous material with varying particle sizes which can be useful in the study of stress concentrations and fracture propagation. It also enables us to produce a criterion for the yield of a peridynamic continuum which has the form of the Tresca hexagonal prism, but with rounded corners.

We introduce the concept of arm elongation to fracture in order to model surface energy in fracture mechanics. Numerical implementation demonstrates that the fracture stress is inversely proportional to the square root of the crack length as predicted by the Griffith theory.