Abstract
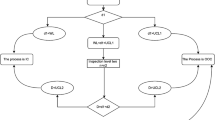
In this article, we propose an attribute control chart for truncated life test under the assumption that the quality characteristic follows the generalized half normal (GHN) distribution. We evaluate the average run length for the proposed control chart. When the average run length is close to the target value, it is termed as a process in control, otherwise, the process is considered to be out of control. Tables for the various values of the shape parameter, the sample size, the specified value of average run length and the process shift constant are presented. Performance of the suggested control chart in the industry is shown by the simulation study and a real-life example is also considered to demonstrate the applicability in the real-life situation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Abbasi B, Guillen M (2013) Bootstrap control charts in monitoring value at risk in insurance. Expert Syst Appl 40:6125–35
Aslam M, Lio YL, Jun C-H (2013) Repetitive acceptance sampling plans for Burr type XII percentiles. Int J Adv Manuf Technol 68:495–507
Chiu J, Kuo T (2008) Attribute control chart for multivariate Poisson distribution. Commun Stat Theory Methods 37:146–58
Chiu J, Kuo T (2010) Control charts for fraction nonconforming in a bivariate binomial process. J Appl Stat 37(10):1717–28
Coorey M, Ananda MMA (2008) A generalization of the half-normal distribution with applications to lifetime data. Commun Stat Theory Methods 37(9):1323–1337
Das N (2008) A note on the efficiency of non parametric control chart for monitoring process variability. Econ Qual Control 23(1):85–93
Gadre MP, Rattihalli RN (2005) Some group inspection based multi-attribute control charts to identify process deterioration. Econ Qual Control 2:151–64
Jolayemi JK (1999) A statistical model for the design of multi-attribute control charts. Indian J Stat Ser B (1960-2002) 61(2):351–365
Li J, Tsung F, Zou C (2012) Directional control schemes for multivariate categorical processes. J Qual Technol 44:136–54
Lu XS, Xie M, Goh TN, Lai CD (1998) Control chart for multivariate attribute processes. Int J Prod Res 36:3477–89
Niaki STA, Abbasi B (2009) Monitoring multi-attribute processes based on NORTH inverse transformed vectors. Commun Stat Theory Methods 38(7):964–79
Patel HI (1973) Quality control methods for multivariate binomial and Poisson distributions. Technometrics 15:103–12
Prajapati DR (2014) Performance of conventional X chart for auto-correlated data using subgroup size often. Int J Innov Res Sci Eng Technol 3(3):105–9
Skinner KR, Runger GC, Montgomery DC (2006) Process monitoring for multiple counts data using a deleted-Y statistic. Qual Technol Quant Manag 3:247–62
Saghir A, Lin Z (2013) Control chart for monitoring Multivariate COM-Poisson attributes. J Appl Stat 41(1):200–14
Stacy EW (1962) A generalization of the gamma distribution. Ann Math Stat 33(3):1187–1192
Wu Z, Luo H, Zhang X (2006) Optimal NP control chart with curtailment. Eur J Oper Res 174:1723–41
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tripathi, H., Saha, M. & Tushaveera, J. Time truncated attribute control chart for generalized half-normal distribution and its application. Life Cycle Reliab Saf Eng 11, 229–235 (2022). https://doi.org/10.1007/s41872-022-00195-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41872-022-00195-2