Introduction

In recent years, geostatistical methods have become a key element of studies in the areas of science where spatial aspects play an essential role (earth sciences, environmental engineering, and environmental sciences). Compared with the procedures of classical statistics, we receive tools that enable the creation of more advanced models of analysed phenomena, which results in better understanding and more precise conclusions. These methods are especially useful in the analysis of spatially continuous phenomena (Webster and Oliver 2007; Zhu 2016). Due to technical and economic limitations, samples for analysis are typically collected by point sampling over the region of interest. Interpolation geostatistical methods enable the construction of maps which present variability of an analysed feature in a continuous way in the area of interest. Depending on fulfilled preconditions, interpolation can be performed using deterministic or stochastic methods. The selection of an appropriate variant depends on the minimum sample size, sampling schedule, distribution of an examined feature, etc. There are several variants of stochastic methods, which are also referred to as kriging methods. The choice of an appropriate variant should be determined by the type of spatial relation of the examined phenomenon and fulfilling of the assumptions (appropriate number of samples, data distribution, stationarity, and isotropy). The advantage of stochastic approach is that it can be used both to interpolate the values at unsampled locations and to model uncertainty or errors of the estimated surface. Deterministic interpolation methods do not incorporate such errors. They predict solely the values at unsampled locations within region of interest using appropriate criteria for selecting the optimal degree of smoothing or similarity.

Using different interpolation methods can lead to different estimations of parameter values at interpolation points, and consequently to the creation of different maps presenting changes in the values of the analysed parameters. For this reason, the selection of an appropriate method is a key element of the conducted analysis.

The aim of the study was to analyse spatial variability of selected parameters of subsurface waters using deterministic interpolation methods. In the study, we compared the following methods: triangulation with linear interpolation (TWL), inverse distance weighting (IDW), modified Shepard’s method (MS), and radial basis function with two systems of basis functions: multiquadratic (RBF–MQ) and thin-plate spline (RBF–TPS).

Geostatistical interpolation and visualization were performed in Surfer®16 software (Golden Software LLC 2018). All further data analyses were carried out using R software (version 3.4.0) (R Core Team 2018).

Materials and Methods

This section contains a brief description of interpolation methods compared here.

The following notations will be used throughout the rest of the paper. Suppose that we are given a set \(S = \left\{ {\underline{{x_{i} }} = \left( {x_{i} , y_{i} } \right):i = 1,2, \ldots ,n} \right\}\) of \(n\) distinct sample points on the plane. In addition, suppose that we are given the values of a real-valued function \(z\left( {x, y} \right)\) at the points in \(S\). Let \(\underline{{x_{0} }} \notin S\) be an arbitrary but fixed interpolation point with coordinates \(\left( {x_{0} , y_{0} } \right)\) at which an interpolated value \(z\left( {x_{0} , y_{0} } \right)\) is required. The symbol \(d\left( {\underline{{x_{0} }} , \underline{{x_{i} }} } \right)\) will be used to denote the Euclidean distance between \(\underline{{x_{0} }}\) and \(\underline{{x_{i} }} \in S\), and \(\omega \left( {\underline{{x_{i} }} | \underline{{x_{0} }} } \right)\) to denote the corresponding weight parameter assigned to \(\underline{{x_{i} }}\). We will generally abbreviate \(z\left( {\underline{{x_{i} }} } \right)\), \(d\left( {\underline{{x_{0} }} , \underline{{x_{i} }} } \right)\), and \(\omega \left( {\underline{{x_{0} }} | \underline{{x_{i} }} } \right)\) to \(z_{i}\), \(d_{i}\), and \(\omega_{i}\), respectively.

Estimates provided by some interpolation techniques employed here (TWL, IDW, and MS) can be represented as a weighted average of the values available at the known points. They share the same general prediction formula:

$$\zeta \left( {\underline{{x_{0} }} } \right) = \mathop \sum \limits_{i = 1}^{n} \omega_{i} z_{i} ,$$
(1)

where \(\zeta \left( {\underline{{x_{0} }} } \right)\) is the estimated value of an attribute at the point of interest \(\underline{{x_{0} }}\), \(\omega_{i}\) represents the weight assigned to the sampled point \(\underline{{x_{i} }}\) with respect to \(\underline{{x_{0} }}\), and \(z_{i}\) is the observed value at the sampled point \(\underline{{x_{i} }}\).

Let us briefly introduce the interpolation methods used in this study.

Triangulation with Linear Interpolation (TWL)

The general idea of TWL algorithm consists in connecting the sampled points into triangles creating a network in such a way that the sides of any of the triangles do not intersect. The function values inside a specific triangle are estimated by a linear interpolation with a weighting mechanism taking into account the coordinates associated with the vertices of the triangle. The advantage of TWL is its simplicity and that it can be used in small data sets. The disadvantages of TWL are that each prediction depends on only three nearby sample points, and the resulting surface is not smooth and TWL does not extrapolate \(\zeta\) values beyond the range of data.

Inverse Distance Weighting (IDW)

The second method—IDW—is based on the assumption that the sampled values \(z_{i}\) closest to the prediction location \(\underline{{x_{0} }}\) have more influence on the predicted value \(\zeta \left( {\underline{{x_{0} }} } \right)\) than those farther away. This causes that predictions are obtained from the nearest sampling points. The weights \(\omega_{i}\) could be written as follows:

$$\omega_{i} = \frac{{d_{i}^{ - p} }}{{\mathop \sum \nolimits_{k = 1}^{n} d_{k}^{ - p} }},$$
(2)

where \(p\) is a positive power parameter and it is chosen arbitrarily (Isaaks and Srivastava 1989). The most common choice for the power parameter is 2. IDW interpolation is easy to use and fast to compute, which makes it very popular. The disadvantages of IDW are sensitivity to outliers and sampling configuration. Furthermore, IDW is always exact interpolation (i.e., no smoothing). Frequently, maps generated from IDW interpolation are characterised by the presence of the “bull’s-eye” effects. IDW is one of the form of the Shepard’s interpolation method (Shepard 1968).

Modified Shepard’s Method (MS)

The next considered method—MS—is the result of modification to classical Shepard’s procedure, developed by Franke and Nielson (1980). MS uses an inverse distance weighted least-squares method and gives similar interpolators to these received from IDW. However, the use of local least-squares eliminates or reduces the “bull’s-eye” patterns, and for large data sets, MS algorithm is faster than original inverse distance weighting algorithm.

Local Polynomial Interpolation (LPI)

LPI fits a local polynomial using a subset of points within the specified neighborhood defined by an ellipse. LPI provides the predicted value at the center of the neighborhood. Noteworthy, the neighborhoods in the covering are allowed to overlap.

Radial Basis Function (RBF)

In this paper, we deal with the following commonly used radial basis function (RBF) methods: the multiquadratic (MQ) method of Hardy (1971, 1990) and the thin-plate spline (TPS) method of Duchon (1977). Given a set \(S\) of sample locations, the RBF approximation at \(\underline{{x_{0} }}\) takes the following form:

$$\zeta \left( {\underline{{x_{0} }} } \right) = \mathop \sum \limits_{i = 1}^{n} \lambda_{i} \varphi \left( {d_{i}^{*} } \right),$$
(3)

where \(d_{i}^{*}\) denotes the parameterized distance between \(\underline{{x_{0} }}\) and \(\underline{{x_{i} }}\) and defined as follows:

$$d_{i}^{*} = \sqrt {\theta_{1} \left( {x_{0} - x_{1} } \right)^{2} + \theta_{2} \left( {y_{0} - y_{1} } \right)^{2} } ,$$
(4)

and \(\theta_{1}\) and \(\theta_{2}\) are fixed positive scalars. In an interpolation, the unknown coefficients \(\lambda_{i}\) are determined by ensuring that the approximation will exactly match the given data at the points in \(S\). This is accomplished by enforcing the interpolation condition \(\zeta \left( {\underline{{x_{i} }} } \right) = z\left( {\underline{{x_{i} }} } \right)\). The usual radial basis functions are Hardy’s multiquadrics with \(\varphi \left( t \right) = \sqrt {1 + t^{2} }\) and thin-plate splines where \(\varphi \left( t \right) = t^{2} { \ln }\left( t \right)\) (Rocha 2009).

Evaluation Criteria for Interpolators

Leave–one–out (LOO) cross validation was adopted for evaluating and comparing the performance of different interpolation methods (Isaaks and Srivastava 1989; Wackernagel 2003). For this procedure, one observation \(z_{i}\) is removed from the data set and the interpolation is performed to generate an estimate \(\zeta_{i}\) at the location \(\underline{{x_{i} }} \in S\) of the removed value. This procedure is then repeated for all locations in \(S\). For each such cross-validation run, an estimate \(\zeta_{i}\) is compared to the true observation \(z_{i}\). In this study, such comparisons are made by means of several error statistics to assess the performance of interpolation methods. Lower values of the error statistics indicate higher accuracy of spatial interpolation. Let us briefly review error statistics which we have considered here for evaluating prediction accuracy (Li 2016).

The root-mean-square error (RMSE) is the most frequently used measure to quantify the accuracy of spatial interpolation. The RMSE is defined as follows:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {z_{i} - \zeta_{i} } \right)^{2} } .$$
(5)

One of the most widely used alternatives to RMSE is the mean absolute error (MAE) which is given by the following:

$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {z_{i} - \zeta_{i} } \right|.$$
(6)

In this paper, two relative-type measures have been used to evaluate the predictive ability of competitive spatial models. Following Li and Heap (2011), we define the relative mean absolute error (RMAE) as follows:

$${\text{RMAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{z_{i} - \zeta_{i} }}{{z_{i} }}} \right|, z_{i} > 0.$$
(7)

This is sometimes referred to as the mean magnitude relative error.

Likewise, a relative counterpart of mean square error (MSRE) takes the form:

$${\text{MSRE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {z_{i} - \zeta_{i} } \right)^{2} }}{{z_{i}^{2} }} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {1 - \frac{{\zeta_{i} }}{{z_{i} }}} \right)^{2} , z_{i} > 0.$$
(8)

Finally, the aforementioned error statistics have been complemented by adopting Willmott’s index of agreement D (Willmott 1981) which is expressed by the following equation:

$$D = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {z_{i} - \zeta_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {z_{i}^{'} } \right| + \left| {\zeta_{i}^{'} } \right|} \right)^{2} }},$$
(9)

where \(z_{i}^{'} = z_{i} - \bar{z}\), \(\zeta_{i}^{'} = \zeta_{i} - \bar{z}\). The index of agreement varies between 0 and 1 where perfect agreement between observed and predicted values is indicated by 1.

Data Source

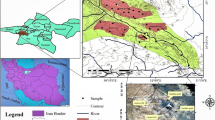
The examination of the quality of subsurface waters was conducted in the valley of the Ciemięga River in the village of Snopków, near Lublin, Poland. The Ciemięga River basin is characterised by its varied relief, and the slope gradients reach 10%. The slopes are generally made of brown soil, whereas the valleys’ bottoms are dominated by bog and muck soil (Orlik et al. 2005). For the purpose of the study, an area of approximately 10 ha was selected, where nine routes were designed (Fig. 1). On each route, four boreholes were made to the depth of 1.5 m for the purpose of collecting water samples. The northernmost borehole on each route was located on the arable land, whereas the other three boreholes were on the grassland. A total of 36 water samples were collected in September 2014. In the samples, \({\text{NH}}_{4}^{ + }\), \({\text{NO}}_{3}^{-} ,\) and \({\text{NO}}_{2}^{-}\) were determined using photometric method. Ammonium was measured with a PC Spectro spectrophotometer from AQUALYTIC, nitrate were determined with a Slandi LF 300 photometer, and nitrite was determined with WTW’s MPM 2010 spectrophotometer.

Fig. 1
figure 1

Water sampling points in the valley of Ciemięga River

Full size image

Results and Discussion

Selected descriptive statistics of the analysed parameters of groundwater quality is presented in Table 1.

Table 1 Descriptive statistics of subsurface water quality parameters
Full size table

In the analysed parameters, the largest range of variability of recorded values was observed for nitrates. The lowest measured value for this index was 0.1 and the highest 97 mg \({\text{NO}}_{3}^{-}\) dm−3. The mean value for \({\text{NO}}_{3}^{-}\) was 12.85 mg \({\text{NO}}_{3}^{-}\) dm−3 and standard deviation reached 24.99 mg \({\text{NO}}_{3}^{-}\) dm−3 and was the highest of all the analysed indices.

The concentration of nitrites in the groundwater samples ranged from 0.04 to 0.82 mg \({\text{NO}}_{2}^{-}\) dm−3. The mean value for \({\text{NO}}_{2}^{-}\) was 0.29 mg \({\text{NO}}_{2}^{-}\) dm−3 and standard deviation was 0.20 mg \({\text{NO}}_{2}^{-}\) dm−3.

In the case of \({\text{NH}}_{4}^{ + }\), the lowest recorded value in the groundwater was 0.04, and the highest 0.97 mg \({\text{NH}}_{4}^{ + }\) dm−3. The mean value and standard deviation were on the levels similar to \({\text{NO}}_{2}^{-}\), and reached 0.30 and 0.22 mg \({\text{NH}}_{4}^{ + }\) dm−3, respectively.

Figure 2 shows the spatial distribution of nitrogen compounds in groundwater used for interpolation.

Fig. 2
figure 2

Spatial distribution of nitrogen compounds in groundwater. Values of \({\text{NH}}_{4}^{ + }\)\({\text{NO}}_{2}^{-}\) and \({\text{NO}}_{3}^{-}\) are presented

Full size image

Nitrates (\({\text{NO}}_{3}^{-}\)) are among the most common groundwater contamination in the world (Spalding and Exner 1993), and when surface waters are transferred, they can worsen water quality and adversely affect ecosystems (Boesch et al. 2001; Rabalais et al. 2001).

The concentration of \({\text{NO}}_{3}^{-}\) in the analysed area was characterised by much greater variability than in the case of other parameters. Almost all positions showed an increase in the parameter in the arable field. Many factors could have influenced this: on one hand, the lack of crops and the limited collection of nitrates by plants; on the other hand, the remains of nitrogen fertilization. \({\text{NO}}_{2}^{-}\) can also be products of mineralization of plant debris. The high content of nitrites may be related to the intensification of nitrification or denitrification processes in which nitrates are a transitional form. The increase in \({\text{NH}}_{4}^{ + }\) concentration usually takes place in autumn and coincides with the growth of other forms of nitrogen. The ammonium content in groundwater in the cultivated field was high. The reason may be the lack of plants in the field and the intensification of mineralization processes of organic matter contained in plant debris and residues after mineral fertilization. The obtained values of parameters are characterised by variability obtained by the other researchers (Orlik et al. 2005; Kennedy et al. 2009).

Next, interpolation with the use of the methods described above (in the case of the IDW method, the power parameter \(p = 2\) was used) as well as cross-validation procedures were conducted for the characteristics of water quality. In particular, RMSE, MAE, RMAE, MSRE, and D were chosen as accuracy criteria for selecting among available interpolation technics. The leave-one-out cross-validation error rates are shown in Table 2.

Table 2 Quantitative measures of model performance
Full size table

In relation to \({\text{NH}}_{4}^{ + }\), MS proved to be the dominating method, which reached the maximum D value and minimum values of the remaining error statistics. TWL method was characterised by the lowest accuracy.

In general, the fittings obtained for \({\text{NO}}_{2}^{-}\) were characterised by a higher accuracy than for \({\text{NH}}_{4}^{ + }\) and had slight divergence. RBF–MQ method reached the best indices RMSE, RMAE, MSRE, and D. TWL method reached the minimum in relation to MAE and the maximum in relation to D. It is important to note that all the indices for MS method were close to the optimal values.

In the case of \({\text{NO}}_{3}^{-}\), it should be emphasized that the measurements were characterised by considerable dispersion, which resulted in the lowest quality of fitting (error statistics reached very high values and variability). As far as RMSE, MAE, RMAE, and D indices are concerned, TWL method reached the highest degree of accuracy, whereas RBF–MQ method obtained the minimum in relation to MSRE.

Visualization of Prediction

For each of the parameters, there were created prediction maps for the methods which were found the best in view of the adopted criteria. Figures 3, 4, 5 show the spatial distribution of nitrogen compounds in groundwater.

Fig. 3
figure 3

Spatial distribution of \({\text{NH}}_{4}^{ + }\) interpolated by MS method (a) and RBF–TPS method (b)

Full size image
Fig. 4
figure 4

Spatial distribution of \({\text{NO}}_{2}^{-}\) interpolated by RBF–MQ method (a) and MS method (b)

Full size image
Fig. 5
figure 5

Spatial distribution of \({\text{NO}}_{3}^{-}\) interpolated by TWL method (a) and RBF–MQ method (b)

Full size image

The best methods for the presentation of spatial distribution of \({\text{NH}}_{4}^{ + }\) concentration in groundwater proved to be MS and RBF–TPS (Fig. 3). On each of the designed routes, the highest \({\text{NH}}_{4}^{ + }\) values were recorded at the northernmost points located on the arable land. At the other points located on the grassland, however, ammonium concentration was lower. Higher \({\text{NH}}_{4}^{ + }\) values on the arable land can be attributed to mineral fertilization for cereals grown in this area. On the maps generated using MS and RBF–TPS methods, the lowest \({\text{NH}}_{4}^{ + }\) values were recorded in the central zone of the analysed area, which was in accordance with the results.

In view of the adopted criteria RBF–MQ and MS proved to be the best methods for generating maps of nitrate spatial distribution in the analysed area (Fig. 4). The maps generated by means of these methods were very similar to each other. The highest \({\text{NO}}_{2}^{-}\) values were found by the northern border of the analysed area and were decreasing in southern direction. High nitrite content in the places where high \({\text{NH}}_{4}^{ + }\) and \({\text{NO}}_{3}^{-}\) concentration values were recorded can be connected with the intensification of nitrification and denitrification processes, in which nitrates constitute transitional forms.

\({\text{NO}}_{3}^{-}\) spatial distribution in the analysed area was presented using TWL and RBF–MQ methods (Fig. 5). This indicator was revealed to display the highest variability of the three analysed indices. The highest nitrate values were found, as it was the case with the other parameters, in the north of the analysed area. This might have been the result of mineral fertilization and the area topography which facilitates surface and subsurface flow of nitrate-polluted water. Substantial decrease of nitrates on the grassland can be attributed to intensive intake of nitrate form, especially that nitrates are highly soluble and easily absorbed by plants. The low concentration of \({\text{NO}}_{3}^{-}\) on the grassland could have also been caused by the reduction of nitrification processes due to a high level of groundwater and smaller thickness of aeration zone at the bottom of the valley.

Spatial distribution analysis of nitrogen compounds in groundwater or soil has received some recent attention in environmental studies. While various aspects of the subject were investigated fairly extensively in research literature, rather, little attention has been paid to the comparison of prediction accuracy. Hong et al. (2007) used two techniques including ordinary kriging and IDW interpolation for presenting spatial variation of groundwater nitrate. In turn, Bernard-Jannin et al. (2017) used IDW method to evaluate spatial and temporal variability of denitrification rates in a floodplain area.

Relatively few papers have dealt with quantitative assessment of accuracy of different spatial interpolation techniques. Notable examples include Kazemi et al. (2017) and Ohmer et al. (2017). The study described in Kazemi et al. (2017) is of particular relevance here. This investigation evaluated the IDW, spline, natural neighbor, and ordinary kriging (OK) methods for estimation of nitrate concentration in groundwater. MRE (mean relative error), RMSE, and %RMSE were considered as the criteria for the evaluation of the accuracy of each method. It was found that the spline and natural neighbor methods produced more accurate estimates than the IDW and OK methods. In the study conducted by Ohmer et al. (2017), a total of nine deterministic (IDW, RBF, LPI, and GPI—global polynomial interpolation) and geostatistical (OK, SK—simple kriging, UK—universal kriging, Co-OK—co-ordinary kriging, and BK—empirical Bayesian kriging) methods were examined for optimal contour mapping of groundwater levels. The comparison was made using seven error statistics: ME (mean error), MSE (mean standard error), MAE, RMSE, RMSSE (root mean standardized error), MAPE (mean absolute percentage error), and Pearson correlation coefficient. In conclusion, geostatistical methods showed better fitting performance than did deterministic methods. Whilst there was not a universal superior method, the most accurate results were provided by Co-OK.

In contrast to these related works, the present paper focuses only on deterministic interpolation methods. For the sake of comparison, we used both the conventional (MAE and RMSE) and relative (RMAE, MSRE, and Willmott’s D) error statistics. Our study revealed that the performance of RBF and MS methods was superior to IDW. It is worth highlighting that: in Ohmer et al. (2017), the LPI method was ranked the highest among the deterministic methods under consideration. Moreover, IDW appeared to be superior to RBF and GPI techniques, which is in contrast to the observations of our study.

Conclusions

The aim of this study was to compare the results of the applied interpolators and finding a method characterised by the highest accuracy of point estimations. The analyses conducted in this study enabled to create the most reliable picture of variability of subsurface water quality parameters in the examined area.

The best of the analysed interpolation methods were RBF–MQ for \({\text{NO}}_{2}^{-}\) as well as the MS method for \({\text{NH}}_{4}^{ + }\). In relation to the parameter \({\text{NO}}_{3}^{-}\), whose distribution was characterised by a very big range, the simplest of the methods—TWL—proved to be the best. On the other hand, it is important to note that IDW method, which is the most frequently used deterministic method (also in the context of comparison with stochastic methods—kriging) (Li and Heap 2011), was characterised by the highest values of RMSE and MAE for \({\text{NO}}_{2}^{-}\) and \({\text{NO}}_{3}^{-}\), and for \({\text{NH}}_{4}^{ + }\), only TWL turned out to be a worse method than IDW. The study results imply that, in the analysis of similar problems (with small sample sizes), the highest accuracy of maps can be obtained when using RBF or MS methods.

It is impossible to find a universal method for choosing interpolation type. The creation of the most reliable picture of spatial variability of an analysed characteristic should always be preceded by the selection of an interpolation method. In the preliminary selection, the following should be taken into consideration: sample sizes, sampling types, and data distribution. After performing specific interpolations, the best method can be selected on the basis of appropriate quality measures.