Introduction

The flood is a natural calamity that occurs as a result of excessive rainfall and geo-climatic conditions in Assam during the monsoon season. Every year, floods occur in the Brahmaputra River in the state of Assam, with the worst flood occurring in August 2000 in the Brahmaputra valley [61]. Floods occur when a river’s capacity is exceeded due to continuous rain or snowmelt. After 1998, the worst flood documented occurred in 2012, where 21 districts out of 27 were affected. Assam’s floods in 2013 were caused by severe rains and damaged 396 villages in 12 districts, destroying about 7000 ha of agricultural land. In 2014 over 42 lakh people were affected and 85 people died as a result of the flood in Assam [61]. Flood also occurred in 2020, during the COVID-19 pandemic situation. In Assam, the floods started in May 2020 due to severe rains that continued until July, affecting 2 to 3 million people across 27 districts. According to the Assam State Disaster Management Authority, over 3000 villages were affected, 44,000 people were relocated to relief camps, and a large portion of agricultural land was damaged [61]. More than half of the territory of Kaziranga National Park and Pobitora Wildlife Sanctuary was devastated by the floods. The flood in 2020 was caused by an extended summer season. According to the meteorological department of Assam, about 1164 mm of rainfall occurred until July, compared to the normal rainfall of 894 mm during the period [61].

Flood is the most devastating and frequent disaster in North-East India, resulting in loss of human life and damage of properties. Although flood problems cannot be eliminated, flood prediction models, as a vital aspect of a flood warning service, can assist in providing timely flood warnings with sufficient lead time for the public to reduce flood losses. Flood routing methods are commonly used as flood prediction models. The effects of floods can be minimized by appropriate modeling, analysis, and management methods. Such modeling and analyzing techniques are hindered in food prediction in an ungauged basin due to the lack of hydro-meteorological data. One of the most difficult current challenges in hydrological research is solving the prediction problem in ungauged basins [78, 86]. However, predictions in ungauged or poorly gauged basins for water resource planning, as well as predictions of global climate change effect even in gauged basins, seem improbable given the present predictive methods or models, which rely largely on calibration [14, 78]. The calibration problem affects the modelling of all hydrological component processes. Among these component processes, flood routing is an important one that is the main focus of this research. Hydraulic and hydrological approaches are used to solve flood routing problems. However, hydraulic-based methods, which generally use the full Saint–Venant equations, are limited in their applicability, due to the lack of availability of topological data and also due to computational limitations of the numerical schemes used in the solution procedure. In this study, alternative ways of overcoming these data and computational problems are proposed by using both hydrologic- and hydraulic-based routing models.

Flood routing is a numerical method, which is used to forecast the variability and celerity of a flood wave as it propagates through a river or a reservoir [81]. Flood routing is a mechanism to ascertain the time is taken and the magnitude of flow at a point on a watershed from known or assumed hydrographs at one or more points upstream [37, 81]. Two main approaches, one based on hydrologic routing and [81] the other based on the hydraulic routing, are typically used to guide flood waves to natural channels. The hydrological method is based on the equation of storage continuity, while the hydraulic method is based on the equations of continuity and momentum consisting of the Saint–Venant equations [11, 13, 24, 47]. The outflow hydrograph at the downstream location can be estimated using a flood routing model by routing a flood event from an upstream gauging station, but in developing countries, most of the basins are ungauged [9, 46]. The Muskingum method is one of the most common and simple hydrologic routing methods for rivers, but its application is restricted to single reach problems [34, 74].

Perumal et al. [66] proposed a Muskingum method in which the calibration is performed by using a nonlinear optimization technique and is capable of solving problems with more parameters. The proposed method was applied using two variants of the Muskingum flood routing methods for accounting the nonlinearity of the channel routing process [66]. Various simplified routing models were created in the twentieth century. Most of these models have been successfully applied to rivers and reservoirs [44]. Due to the adequacy and reliable relationship between their parameters and channel properties, the Muskingum method [58] and the Muskingum-Cunge method [29] are widely adopted and used in flood routing models [38, 43, 45]. The Muskingum model investigates a method of parameter estimation to determine the weight coefficient X and wave travel time K. Most of the methods are optimization techniques, including the method of trial and error, recession analysis [85], least-square procedure [3], feasible sequential quadratic programming [51], chance-constrained optimization (A. [30, 31], genetic algorithm (J. [22], particle swarm optimization [27], harmony search [48], Broyden-Fletcher-Goldfarb-Shanno technique [40], immune clonal selection algorithm (J. [57], and hybrid algorithm [55, 84]. However, due to their need for large amounts of observed data, these studies and methods are more applicable to flood routing in gauged basins.

The hydraulic routing method is based on the Saint–Venant equations composed of the continuity and momentum equations. The hydraulic routing model involves the numerical solution of the one-dimensional Saint–Venant Equation in open channel flow [67]. Generally, the Saint–Venant momentum equation is simplified by neglecting some terms and is divided into three primary forms. The first form is the Kinematic wave model, which presumes that gravity and friction forces balance each other. The second form is the diffusive wave model, which presumes that pressure forces are significant, in addition to gravity and frictional forces. Another form is the dynamic wave model, where both inertial and pressure forces are significant, and the backwater effects are also considered. The kinematic wave routing method can transform the flood wave with the help of the system without attenuation of the peak flow [64]. The kinematic wave routing model helps to calculate the resulting changes in flow, velocity, and depth associated with the flow waves (Ambrose B Robert, 2017). To solve kinematic wave hydraulic routing, finite difference and finite element methods are used. Chapra [19] has described an explicit method to solve the kinematic wave routing method. However, a partially implicit method is narrated by [26], and a fully implicit method is used in USEPA’s Water Quality Analysis Simulation Program (WASP) (Ambrose B Robert, 2017). The most widely used approximation is diffusion wave routing. Several researchers presented a variety of diffusive wave models [8],A. S. [21, 35, 54, 79]. Roohi et al. [73] carried out numerical, dynamic wave, kinematic wave, Att-Kin, and Muskingum models to perform flood routing in the Mehrian River Range. Their main aim was to evaluate the flood routing and zoning methods in the Mehrian waterway and to present a new mathematical equation to predict the maximum flow width and flood plain in the study area. Luo [56] attempts to determine the best kinematic wave scheme for open-channel routing in Peace River, Canada. Munoth and Goyal [62] analyzed the drainage characteristics of the Upper Tapi River by Shuttle Radar Topography Mission (SRTM) Digital Elevation Model (DEM) using Geographic Information System (GIS) tools. The QSWAT (Soil and Water Assessment Tool) model was used to calculate the hydrological parameters. The model performance was evaluated using R2 (R-square) (0.75), Nash–Sutcliffe efficiency (ENS) (0.75), and percent bias (PBIAS) (1.1) values, and the result shows excellent agreement between observed and simulated discharge. The R2 values for the drainage density (Dd), sediment yield, and evapotranspiration vary from 0.30 to 0.40. They performed the integration of morphometric parameters, GIS, and QSWAT models to overcome the challenge of scarcity of observed data. Abdulkareem et al. [1] conducted several studies to examine the compatibility of model results with streamflow measurements and concluded that hydrological models are essential tools for water resources planning and management.

The dynamic wave model is a hydraulic routing model that includes all the terms of the momentum equation of Saint–Venant equations and has been widely used as a river flood routing method (X. Q. [87]. The Saint–Venant equations are nonlinear, and to solve these equations, numerical methods are used considering all the terms of the Saint–Venant equations [26, 59],Y. [88]. The numerical model for hydraulic dynamic wave model based on Saint–Venant equations was developed to study the behavior of the propagation of flood waves in trapezoidal channels [80]. Numerical solutions of the Saint–Venant equations are available in the direct form or in the characteristic form. The direct form of Saint–Venant equations is solved by finite element and finite difference methods in the implicit form [5,6,7, 10, 33, 36, 50, 53, 67, 70]. The Saint–Venant equations have been discrete in implicit and explicit forms without considering lateral inflow and numerically solved for the dynamic wave model for a trapezoidal and triangular channel [71]. Akbari and Barati [2] mentioned that the sensitivity analysis is required for effectively using a model as it helps the model user to understand the significance of variables and the effects on computed outputs of errors in inputs. The sensitivity analysis of flood routing parameters using an implicit numerical scheme was investigated by numerical, statistical, and field measurement procedures in three unmanaged catchments in the Persian Gulf region. The results indicate that peak inflow, roughness coefficient, bed slope, bed width, river length, side slope, weighting factor, and the base flow are the important rankings of different parameters for output results.

In an ungauged basin, a rainfall-runoff model can be really helpful in the case of calculating discharge. A rainfall-runoff model is a mathematical approach that describes the relationship between rainfall and runoff of a catchment, drainage basin, or watershed. In the rainfall-runoff model, a rainfall hyetograph is input and it gives surface runoff hydrograph of that rainfall hyetograph. In other words, the rainfall-runoff models calculate the conversion of rainfall into surface runoff. The conversion of rainfall into surface runoff over a drainage basin or catchment area is known to be a very complex hydrological phenomenon, as this process is highly nonlinear, time-varying, and spatially distributed. Over the years, researchers have developed many models to simulate the rainfall-runoff model.

In the literature that has been reviewed, there is evidence of potential for use of dynamic flow routing. The models require flow data to calibrate the parameters, even for the physically based models as it has been found that the parameters could not be directly measured. However, it is not unusual to work with catchments that have only partial sets of stream flow data, or no data at all. For instance, in the UK, the network of 1400 flow gauging stations is extensive but still insufficient to cover the entire network of rivers [77]. The catchments with inadequate stream flow data are classified as ungauged [78]. The International Association of Hydrological Sciences (IASH) has recognized the need to shift the main focus of hydrology from gauged to ungauged catchments. A dynamic method will be most suitable if the required input data is available, but the hydrologic method may also provide better flood forecasting results for ungauged basins. Several studies have been carried out on the comparison of hydrological versus hydraulic routing methods [39, 52, 69], but these have not been performed in ungauged basins. This study will focus on the development of suitable flood routing method for ungauged basin in North-East India. In the present work, the Kulsi River Watershed, which lies in Meghalaya and Assam, India, has been selected as the area of study. Rainfall-runoff modeling was simulated by the SCS-CN method to obtain an inflow hydrograph at the upstream of an ungauged basin. In this study, both hydrologic and hydraulic routing models are adopted to estimate the outflow hydrograph at the downstream section of the Kulsi River Basin. A new approach of the Muskingum method and the modified Cunge-Muskingum method is used in this study as hydrologic routing models because of its simplicity as well as its ability to perform flood routing in an ungauged basin. Various hydraulic routing models are also used in this study because of their accuracy as well as their ability to obtain other parameters (i.e., depth of flow, area, and velocity) at any section of the channel. In this study, kinematic wave model, diffusive wave model, and dynamic wave model are used as hydraulic routing models.

Channel Routing Methods

Muskingum Approach

The Muskingum method of flood routing approximates the storage volume in a river by considering prism storage and wedge storage. To calculate prism and wedge storage two Muskingum parameters K and X are required to be obtained. K is the time of travel of the flood wave through the channel reach, and X is the weight factor. Previous-year inflow and outflow hydrographs of a channel reach are used to obtain Muskingum parameters K and X. However, in the case of ungauged basins, the previous-year upstream and downstream discharge data are not available and the estimation of Muskingum parameters is not possible using the conventional method. Therefore, an approach is explored in this study to determine the Muskingum parameters for the ungauged basin. 

In this approach, the Muskingum parameters K and X are estimated for the ungauged basin using an inflow hydrograph of the current year, flow characteristics, and dimension of the channel. The Muskingum parameter K can be obtained using Eq. (1) [26, 38]:

$$K=\frac{\Delta L}{{V}_{c}}$$
(1)

where.

  • K = wave travel time (s).

  • ΔL = length of channel reach (m).

  • Vc = wave celerity (m⋅s−1).

For a parabolic cross channel section, the wave celerity (Vc) may be estimated from Table 1. [82]:

$${V}_{c}=\frac{11}{9}{V}_{av}$$
Table 1 Wave celerity (Vc) for various channel shapes [82]
Full size table

Using Manning’s equation for parabolic channel section:

Manning’s roughness equation is used to calculate the average velocity (Vav) [26]:

$${V}_{av}=\frac{1}{n} {R}^\frac{2}{3} \sqrt{S}$$
(3)

where.

  • n = manning roughness coefficient.

  • R = hydraulic radius of the channel (m).

  • S = slope of the channel (m/m).

The section factor can be calculated using Manning’s equation [26]:

$$A{R}^\frac{2}{3} = \frac{{Q}_{o}.n}{\sqrt{S}}$$
(4)

where.

  • A = cross-sectional area of flow (m2).

  • Q0 = reference flow (m3 s−1).

Equation for reference flow was given by [83]:

$${Q}_{o}=0.5({Q}_{p}-{Q}_{b})$$
(5)

where.

  • Qb = minimum discharge (m3 s−1).

  • Qp = peak discharge (m3 s−1).

The wetted perimeter of the channel with discharge for natural rivers follows Lacey’s theory (for stable River channels) presented in Eq. (6) [68].

$$PS=C\sqrt{{Q}_{o}}$$
(6)

where.

  • P = wetted perimeter of the channel (m).

  • C = coefficient of perimeter (between 4.71 and 4.81).

When the top width of the flow exceeds the mean depth of flow with a factor of 20 m, then the hydraulic radius (R) and hydraulic depth (d) can be assumed to be equal [12, 25]. Since most of the river channel which reaches the flow depth is small relative to the top width of the channel reach (W), the wetted perimeter (P) may be assumed to be equal to W. The equation for the area of the parabolic channel section is presented in Eq. (7) [25]:

$$A=\frac{2yW}{3}$$
(7)

where.S

  • y = depth of flow (m).

  • W = top width of the flow (m).

For wide parabolic cross-section channels, the hydraulic radius is estimated (Eq. (8)) from Table 2.

$$R\cong d=\frac{2}{3}y$$
(8)

where.

Table 2 Hydraulic depth for different channel sections [25]
Full size table

d = hydraulic depth (m).

Now substituting in Eq. (4) for a parabolic section:

$$A{R}^\frac{2}{3} =\frac{2yW}{3}\times {(\frac{2}{3}y)}^\frac{2}{3}=\frac{{Q}_{o}.n}{\sqrt{S}}$$
(9)

But P is assumed to be approximately equal to W and hence P can be substituted in Eq. (9) to solve for y as shown in Eq. (10) [81]:

$${y=(\frac{{Q}_{o}.n}{0.508P\sqrt{S} })}^\frac{3}{5}$$
(10)

The top width of the channel (W \(\cong\) P), reference flow \(({Q}_{o})\), slope of the channel (S), wave celerity (Vc), and reach length of the channel (ΔL) are used to estimate the Muskingum parameter X as shown in Eq. (11) [26, 38]:

$$X=\frac{1}{2}-\frac{{Q}_{o}}{2.S.P.{V}_{c}.\Delta L}$$
(11)

Three routing coefficients are determined by using Eqs. (12), (13), and (14):

$${C}_{o}=\frac{\Delta t+2KX}{m}$$
(12)
$${C}_{1}=\frac{\Delta t-2KX}{m}$$
(13)
$${C}_{2}=\frac{2K\left(1-X\right)-\Delta t}{m}$$
(14)

where

$$m=[2K\left(1-X\right)+\Delta t]$$
(15)

The three routing coefficients are used to estimate the discharge at the downstream section (Eq. (16):

$${Q}_{j+1}={C}_{o}{I}_{j+1}+{C}_{1}{I}_{j}+{C}_{2}{O}_{j}$$
(16)

where.

  • Qj = outflow at time (t).

  • Ij = inflow at time (t).

According to Viessman et al. [82], negative values of C1 must be avoided. Negative values of C2 do not affect the routed hydrographs. The negative values of C1 can be avoided by satisfying Eq. (17):

$$\frac{\Delta t}{K}>2X$$
(17)

Cunge-Muskingum Method (Modified Muskingum Method)

Cunge [29] proposed the Cunge-Muskingum method based on the Muskingum method, a method traditionally applied to linear hydrologic storage routing. Bharali and Misra [17] modified the Muskingum routing equation which is written as Eq. (18), for the discharge at x = (i + 1) ∆x and t = (j + 1) ∆t:

$${Q}_{i+1}^{j+1}={C}_{o}{Q}_{i}^{j+1}+{C}_{1}{Q}_{i}^{j}+{C}_{2}{Q}_{i+1}^{j}$$
(18)

where C0, C1, and C2 are the routing coefficients.

$${C}_{o}=\frac{\Delta t+2KX}{m}$$
(19)
$${C}_{1}=\frac{\Delta t-2KX}{m}$$
(20)
$${C}_{2}=\frac{2K\left(1-X\right)-\Delta t}{m}$$
(21)

where

$$m=[2K\left(1-X\right)+\Delta t$$
(22)

In Eqs. (19) through (21), K is a travel time having dimensions of time and X is a factor expressing the relative influence of inflow on storage levels. Equation (18) gives an approximate solution of a modified diffusion equation.

$$K=\frac{\Delta x}{{c}_{k}}= \frac{\Delta x}{dQ/dA}$$
(23)
$$X=\frac{1}{2}1-\left(\frac{Q}{B{c}_{k}{S}_{0}\Delta x}\right)$$
(24)

where ck is the celerity of wave corresponding to Q and B, and B is the top width of the surface water. Cunge [29] showed that for numerical stability,it is required that 0 ≤ X ≤ 1/2.

Kinematic Wave Model

Kinematic waves govern flow when inertial and pressure forces are not important. Kinematic waves administer the flow when local acceleration, convective acceleration, and pressure forces of the momentum equation of Saint–Venant equations are less significant. For a kinematic wave, the energy grade line is parallel to the channel bottom and the flow is steady and uniform (So = Sf) within the differential length. The solution of the kinematic wave equations enumerates the diffusion of flow as a function of distance x across the channel at a time t. The solution can be derived either by analyzing simultaneously the characteristics equations or by using the finite difference method. Bharali and Misra [15] investigate the flood routing using the kinematic wave model (KWM) and variable kinematic wave model (VPKWM) for the non-prismatic natural channel in an ungauged basin. In the present study, both the methods were employed as a hydraulic routing method to predict the flood hydrograph at the outlet of an ungauged basin. The equations used for KWM and VPKWM for the unknown \({Q}_{i+1}^{j+1}\) are Eqs. (25) and (26), respectively.

$${Q}_{i+1}^{j+1} = \frac{\left[\frac{\Delta t}{\Delta x}{Q}_{i}^{j+1}+\alpha \beta {Q}_{i+1}^{j}{\left(\frac{{Q}_{i+1}^{j}{+ Q}_{i}^{j+1} }{2}\right)}^{\beta -1}+ \Delta t\left(\frac{{q}_{i+1}^{j+1}{+ q}_{i+1}^{j} }{2}\right)\right] }{\frac{\Delta t}{\Delta x} + \alpha \beta {\left(\frac{{Q}_{i+1}^{j}{+ Q}_{i}^{j+1} }{2}\right)}^{\beta -1}}$$
(25)
$${Q}_{i+1}^{j+1} = \frac{\left[\frac{\Delta t}{\Delta x}{Q}_{i}^{j+1}+\alpha (i,j)\beta {Q}_{i+1}^{j}{\left(\frac{{Q}_{i+1}^{j}{+ Q}_{i}^{j+1} }{2}\right)}^{\beta -1}+ \Delta t\left(\frac{{q}_{i+1}^{j+1}{+ q}_{i+1}^{j} }{2}\right)\right] }{\frac{\Delta t}{\Delta x} + \alpha (i,j)\beta {\left(\frac{{Q}_{i+1}^{j}{+ Q}_{i}^{j+1} }{2}\right)}^{\beta -1}}$$
(26)

where α(i,j) = [\(n({P(i,j))}^\frac{2}{3}/\sqrt{{S}_{0}})\)] 0.6 and β = 0.6.

Diffusive Wave Model

Flood routing is a mechanism to ascertain the time taken and the magnitude of flow at any section of a stream from known or assumed hydrographs at one or more sections at upstream. The activity turns out to be complicated when applied to flows in irregularly shaped channels, for example, rivers with inundated floodplain zones [65]. Hydraulic flood routing is based on the solution of partial differential equations of Saint–Venant equations. The Saint–Venant equations (Saint–Venant, 1871) are nonlinear hyperbolic equations. The Saint–Venant equations include the continuity equation and the momentum equation, which describe the unsteady flow in rivers and open channels. The Saint–Venant equations for distributed routing are not amenable to analytical solutions except in a few exceptional simple cases. Generally, the Saint–Venant momentum equation is simplified by neglecting some terms and is divided into three primary forms. The first form is the kinematic wave model, which presumes that gravity and friction forces balance each other. The second form is the diffusion wave model, which presumes that pressure forces are significant, in addition to gravity and frictional forces. Another form is the dynamic wave model, where both inertial and pressure forces are significant, and the backwater effects are also considered. The application of a diffusive wave model in an ungauged basin is difficult due to the non-availability of hydro-morphological data. Bharali and Misra [18] developed a diffusive wave flood routing model (DWFRM) for an ungauged basin, which is used in this study as a diffusive wave hydraulic routing model for prediction of flood hydrograph at the outlet of an ungauged basin. The equation used for DWFRM for the unknown \({Q}_{i+1}^{j+1}\) is Eq. (27):

$${Q}_{i+1}^{j+1}=\frac{{\alpha }_{i}^{j}.{ Q}_{i}^{j+1}- {\beta }_{i}^{j}.\Delta x}{{\alpha }_{i}^{j}}$$
(27)
$${A}_{i+1}^{j+1}=\frac{{ A}_{i+1}^{j}.\Delta x-{ (Q}_{i+1}^{j+1}.\Delta t - { Q}_{i}^{j+1}.\Delta t)}{\Delta x}$$
(28)

where

$${\alpha }_{i}^{j}=\frac{\frac{3g}{2 T}}{\frac{{Q}_{i}^{j}}{{A}_{i}^{j}}\left[\frac{5}{3}-\frac{8{{A}_{i}^{j}}^{2}}{{PT}^{3}}\right]}$$
(29)

and

$${\beta }_{i}^{j}=g\left({{{s}_{f}}_{i}^{j}-s}_{0}\right)$$
(30)

\({\alpha }_{i}^{j}\) and \({\beta }_{i}^{j}\) values can be easily calculated from Eqs. (29) and (30) using initial and boundary data at the starting point, then the rate of flow is calculated from Eq. (27). Finally, the cross-sectional area can be calculated as shown in Eq. (28). In the proposed DWFRM model, the hydrograph at the downstream end of the channel section enters at the upstream of the next channel section and establishes the upstream boundary conditions. The details of the diffusive model (DWFRM) can be found in Bharali and Misra [18].

Dynamic Wave Model

Flood routing in natural rivers can be investigated using the full Saint–Venant equations. Flood routing methods used for simulation of flood events commonly follow hydraulic and hydrologic approaches. The dynamic wave model is a hydraulic routing model that includes all the terms of the momentum equation of Saint–Venant equations and has been widely used as a river flood routing method (X. Q. [87]. The Saint–Venant equations are nonlinear, and to solve these equations, numerical methods are used considering all the terms of the Saint–Venant equations [26, 59],Y. [88]. The numerical model for the hydraulic dynamic wave model based on Saint–Venant equations was developed to study the behavior of the propagation of flood waves in trapezoidal channels [80].

A new form of momentum equation of Saint–Venant equations has been derived for a hypothetical cross section having a parabolic cross-sectional channel [16]. The simplified momentum equation and the continuity equation are solved by an implicit difference scheme in order to anticipate the outflow hydrograph at the downstream end for a parabolic channel section with constant width. The proposed modified dynamic wave model for the parabolic channel (MDWMP) was derived from the general Saint–Venant equations by considering the derivative  to be negligible in comparison to the other terms of the equation, and the in-depth details of the proposed model were presented in Bharali and Misra [16].

$${Q}_{i+1}^{j+1}=\frac{{ Q}_{i+1}^{j}.\Delta x+{\alpha }_{i}^{j}.{ Q}_{i}^{j+1}.\Delta t- {\beta }_{i}^{j}.\Delta x.\Delta t}{\Delta x+\alpha .\Delta t}$$
(31)
$${A}_{i+1}^{j+1}=\frac{{ A}_{i+1}^{j}.\Delta x-{ Q}_{i+1}^{j+1}.\Delta t- { Q}_{i}^{j+1}.\Delta t}{\Delta x}$$
(32)

where

$${\alpha }_{i}^{j}=\frac{2.{Q}_{i}^{j}}{{A}_{i}^{j}}+\frac{\frac{3.g.{A}_{i}^{j}}{2.T}-\frac{{{Q}_{i}^{j}}^{2}}{{{A}_{i}^{j}}^{2}}}{\frac{{Q}_{i}^{j}}{{A}_{i}^{j}}\left[\frac{5}{3}-\frac{8{{A}_{i}^{j}}^{2}}{{PT}^{3}}\right]}$$
(33)

and

$${\beta }_{i}^{j}=g{A}_{i}^{j} \left({{{s}_{f}}_{i}^{j}-s}_{0}\right)$$
(34)

\({\alpha }_{i}^{j}\) and \({\beta }_{i}^{j}\) values can be easily calculated as shown in Eqs. (33) and (34) using initial and boundary data at the starting point, then the rate of flow is calculated as shown in Eq. (31). Finally, the cross-sectional area can be calculated as shown in Eq. (32).

Applications of the Routing Models

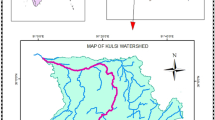
The channel routing models are applied in the Kulsi River Basin, which is a part of the Brahmaputra sub-basin, which is hypothetically considered an ungauged basin. The drainage area of the study area is 2822.99 km2. The Kulsi River Basin encompasses two states in northeast India (Assam and Meghalaya). The downstream of the basin experiences large floods. It is on the south bank of the River Brahmaputra. It is located between latitude 25° 20′ N to 26° 20′ N and longitude 90° 00′ E to 91° 50′ E (Fig. 1). Digital elevation models (DEMs) are being widely used for watershed delineation, extraction of stream networks, and characterization of watershed topography (elevation map, slope map, and aspect map) by using watershed delineation tool in ArcGIS software. The DEM used in this study is collected from CartoSat 1_V3_R1 (). CartoDEM version_3R1 is a national DEM developed by the Indian Space Research Organization (ISRO). CartoDEM version_3R1 has a resolution of 30 × 30 m (or 1 arc sec). The soil data for this project was obtained from the Food and Agriculture Organization (FAO) soil portal (Harmonized World Soil Database v 1.2). The soil data for the study area was downloaded from the Food and Agriculture Organization (FAO). The soil texture of the Kulsi River Basin consists of Loam, sandy loamy, and clay loam. The land use and land cover (LULC) classification for the Kulsi River Basin is done by performing supervised image classification as per the required class sample using ArcGIS 10.1. Linear Imaging Self Scanning Sensor (LISS)-III Satellite image is used in this project to perform Supervised Image Classification. The LISS-III image is downloaded from Bhuvan. The LULC of the Kulsi River Basin consists of an agricultural field, dense forest, open area, open forest, and residential area.

Fig. 1
figure 1

Location of Kulsi River Watershed

Full size image

Eight lateral inflows have been identified contributing to the main Kulsi River. Sub-basins for inflows are delineated using ArcGIS 10.1. In this study, the Ukiam Dam site is considered as the upstream of the Kulsi River Basin, and the conflict with River Brahmaputra is considered as an outlet of the Kulsi River Basin. For this study, field rainfall data for the month of May and June 2010 were collected from the Indian Metrological Department (IMD), Guwahati. The rainfall data is distributed over the study area using the inverse distance weighted (IDW) method in Arc GIS 10.1.

Flood routing is a procedure to determine the magnitude of flow at a point in the downstream end of a watercourse from the known inflow hydrograph at the upstream gauge station.

$$Q = \frac{{\left(P- {l}_{a}\right)}^{2}}{P-{l}_{a }+ S}\mathrm{ if }P > Ia,\mathrm{ otherwise }Q = 0$$
(35)

where.

P is the total rainfall (mm).

Ia is the initial abstraction = 0.2S.

S is the potential maximum retention (mm)

$$S=\frac{25400}{CN}-254$$
(36)

where CN is the curve number.

The inflow hydrograph and lateral inflow hydrographs are determined by using the SCS-CN rainfall-runoff model using Eqs. (35) and (36). The length of the Kulsi River from the Ukiam Dam site (upstream) to the outlet of the basin is 75.8 km, the bottom slope of the channel is 5.41 × 10−4, and the Manning’s coefficient is 0.035. For the accuracy of the results and for the stability of the model \(c\frac{\Delta t}{\Delta x}\) is smaller than Courant criteria, where c is the velocity of the flow in m/s. The spacing interval was selected as \(\Delta x=15,\) and the time interval as \(\Delta x=2 hr\). The computed outflow hydrograph at the outlet of the Kulsi River Basin using the abovementioned routing models is presented in Fig. 2.

Fig. 2
figure 2

Computed outflow hydrographs with the observed hydrograph at the outlet of the Kulsi River Basin

Full size image

Performance of the Routing Models

In the present study, different statistical goodness-of-fit approaches were used to evaluate the performance and validation of all the proposed routing models. The fundamental goal is to have a simulated output that is more similar to the observed output, and therefore the goal is to minimize the objective function. In general, various goodness-of-fit criteria favor different hydrograph components (volumes, peak flows, time of peak, etc.) and may assign greater weight to a certain element of discrepancy between observed and simulated findings. As a result, there is no universal criterion, and the one that is finally chosen should be determined by the goal of the modelling exercise [20].

The following criteria were used to evaluate the performance of the above-mentioned model:

  1. 1.

    In order to compare the proposed model output with the data observed, the criteria for making such a comparison must first be identified (Green Ira & D, 1985). In the present study, the difference between the observed and the computed hydrograph was analyzed by the root mean square error (RMSE). The RMSE evaluates the magnitude of the error in the computed hydrographs (J. K. [32, 76] and is given by

$$RMSE=\sqrt{\frac{\sum_{\mathrm{i}=1}^{\mathrm{n}}{\left({Q}_{comp} - {Q}_{obs}\right)}^{2}}{\mathrm{n}}}, i = 1, 2, 3, . . .. n$$
(37)

In this equation, Qcomp represents the computed outflow, and Qobs represents the observed outflow.

  1. 2.

    The criterion for the difference between computed and observed peak discharge (E-peak) (Green Ira & D, 1985) is given by

$$E-peak =\frac{{Q}_{p,comp}- {Q}_{p,obs}}{{Q}_{p,obs}}x 100$$
(38)

The above equation shows the percentage of error in the peak discharge. In the present study, the peak flood discharge at the outlet of the basin obtained from the computed flood hydrograph was compared with the observed flood hydrograph. In Equation (38), Qp,,comp is the computed peak flows in m3/s, and Qp,,obs is the observed peak flows in m3/s.

  1. 2.

    The criterion for the difference between computed and observed peak discharge time (E-time) is given by

$$E-time =\frac{{t}_{p,comp}- {t}_{p,obs}}{{t}_{p,obs}}x 100$$
(39)

The above equation shows the percentage of error in peak discharge time. In the present study, the peak flow time for the computed and observed flood hydrograph was compared. In the abovementioned equation, tp, comp is the time taken by the computed hydrograph to reach the peak flow in hours, and Qp,obs is the time taken by the observed hydrograph to reach the peak flow in hours.

  1. 3.

    The criterion for the difference between the total volume of computed and observed hydrographs (E-volume) is given by:

$$E-volume =\frac{ {V}_{comp}- {V}_{obs}}{{V}_{obs}}\times 100$$
(40)

The above equation shows the percentage of error in the total volume of the computed hydrograph. In the present study, the total volume was compared for computed and observed flood hydrographs. In the abovementioned equation, Vcomp is the total volume of the computed hydrograph in cubic meters and Vobs is the total volume of the observed hydrograph in cubic meters.

  1. 4.

    Relative error (RE) is given by

$$RE=\frac{\left|{Q}_{o}-{Q}_{p}\right|}{{Q}_{o}}\times 100\mathrm{ \%}$$
(41)

The above equation shows the relative percentage error. In the abovementioned equation, Qo is the observed data at the time t, and Qp is the predicted value at the time t. The relative error is used to determine the percentage of samples belonging to one of the three groups [28]:

  • RE ≤ 15% indicates “low relative error.”

  • 15% < RE ≤ 35% indicates “medium error.”

  • RE > 35% indicates “high error.”

  • Mean absolute error (MAE) [23] is given by

$$MAE=\frac{1}{n}\sum\nolimits_{i=1}^{n}\left|{Q}_{o}-{Q}_{p}\right|$$
(42)

In the above equation, n is the number of samples, Qo is the observed data at the time t, and Qp is the predicted value at the time t. The mean absolute error is the most basic metric of forecast accuracy (MAE). The mean absolute error is just the average of the absolute errors, as the name implies. The absolute error is defined as the absolute value of the difference between the predicted and actual values. For continuous data, the mean absolute error (MAE) is used to assess accuracy. The mean absolute error calculates the average magnitude of errors in a series of predictions without taking into account their direction. The mean absolute error is the average of the absolute differences between prediction and actual observation over the test sample, where all individual deviations are given equal weight. The mean absolute error and root mean square error are both measures of average model prediction error expressed in units of the variable of interest. The mean absolute error and the root mean square error can both vary from 0 to ∞ and are independent of error direction.

  1. 7.

    Correlation coefficient (r) is given by

$$r=\frac{\sum_{i=1}^{n}({Q}_{o}-{Q}_{m})({Q}_{p}-{Q}_{mp})}{\sqrt{\sum_{i=1}^{n}{({Q}_{o}-{Q}_{m})}^{2}}\sqrt{\sum_{i=1}^{n}{({Q}_{p}-{Q}_{mp})}^{2}}}$$
(43)

In the abovementioned equation, n is the number of samples, Qo is the observed discharge at the time t, Qp is the predicted discharge at the time t, Qmp is the mean of predicted discharge, and Qm is the mean of observed discharge. R-squared correlation is an important statistical measure that represents the proportion of the difference or variance in statistical terms for a dependent variable that can be explained by an independent variable or variables in a regression model. In short, R-squared correlation indicates how well data fits the regression model or how well modelled data fits observed data. R2 is the coefficient of determination, while R is the correlation coefficient. The correlation coefficient formula determines the strength of a linear relationship between two variables.

  1. 8.

    Nash-Sutcliffe efficiency (NSE) (Nash & Sutcliffe, 1970) is given by

$$NSE=1-[\frac{\sum_{i=1}^{n}{({Q}_{o}-{Q}_{p})}^{2}}{\sum_{i=1}^{n}{({Q}_{o}-{Q}_{m})}^{2}}]$$
(44)

In the above equation, n is the number of samples, Qo is the observed data at the time t and Qp is the predicted value at the time t, and Qm is the mean of observed discharge. Moriasi et al. [60] recommended the following model performance ratings:

  • NSE ≤ 0.50 indicates unsatisfactory.

  • 0.50 < NSE ≤ 0.65 indicates satisfactory.

  • 0.65 < NSE ≤ 0.75 indicates good.

  • 0.75 < NSE ≤ 1 indicates very good.

The Nash-Sutcliffe efficiency (NSE) is a normalized statistic that calculates the relative magnitude of residual variance vs observed data variance (Nash and Sutcliffe, 1970). The Nash-Sutcliffe efficiency measures how well the observed vs simulated data plot follows the 1:1 line. NSE = 1 denotes a perfect fit of the model to the observed data. NSE = 0 implies that the model predictions are as accurate as the observed data mean, whereas infinity < NSE < 0 indicates that the observed mean outperforms the model.

  1. 9.

    Kling-Gupta efficiency (KGE)

Gupta et al. [42] developed this goodness-of-fit measure to provide a diagnostically interesting decomposition of the efficiency of Nash-Sutcliffe efficiency, which facilitates the analysis of the relative importance of its various components. In the context of the hydrological modelling, Kling et al. [49] proposed a revised version of this index to ensure that the bias and variability ratios are not cross correlated.

$$KGE=1-[\sqrt{({CC-1)}^{2}+({\frac{cd}{rd}-1)}^{2}+({\frac{cm}{rm}-1)}^{2}} ]$$
(45)

where CC is the Pearson coefficient value, rm is the average of observed values, cm is the average of predicted values, rd is the standard deviation of observation values, and cd is the standard deviation of predicted values. Rogelis et al. [72] consider model performance to be “poor” for 0.5 > KGE > 0. Schönfelder et al. [75] consider negative KGE values as “not satisfactory.”

Pearson correlation coefficient (CC) is the test statistics that measures the statistical relationship, or association, between two continuous variables. It is known as the best method of measuring the association between variables of interest because it is based on the method of covariance. It gives information about the magnitude of the association, or correlation, as well as the direction of the relationship. The Pearson correlation coefficient is a measure of the strength of the linear relationship between two variables.

$$CC=\frac{\sum_{i=1}^{n}\left({O}_{i}-\overline{O }\right)({P}_{i}-\overline{P })}{ \sqrt{\sum_{i=1}^{n}{\left({O}_{i}-\overline{O }\right)}^{2}} \sqrt{\sum_{i=1}^{n}{({P}_{i}-\overline{P })}^{2}}}$$
(46)

where Oi is the observation value, Pi is the forecast value, ‘\(\overline{O }\)’ is the average of observation values, and ‘\(\overline{P }\)’ is the average of forecast values.

Result and Discussion

The outflow hydrographs at the Kulsi River outlet developed by using the flood routing models (Muskingum approach, Cunge-Muskingum model, KWM, VPKWM, DWFRM, and MDWMP), and the observed data collected from the National Institute of Hydrology (N.I.H), Guwahati, are presented in Fig. 2. From the graphical presentation, it is difficult to compare the performance of the proposed models with the observed data. Therefore, in the present study, it is tried to evaluate the performance of the models by estimation statistical errors (Tables 3 and 4). In this study, nine statistical errors (RMSE, E-peak, peak flow time error, E-volume, MAE, r-square, RE, NSE, and KGE) are used to evaluate the performance of the proposed models. The r-square values of the proposed models are presented in Fig. 3.

Table 3 Computation of different statistical error (RMSE, E-peak, peak flow time error, E-volume, MAE, and r-square) for the proposed models (Kulsi River Basin)
Full size table
Table 4 Computation of different statistical error (RE, NSE, and KGE) for the proposed models (Kulsi River Basin)
Full size table
Fig. 3
figure 3

R-square values for the different flood routing models

Full size image

In this study, both hydrologic and hydraulic routing models are considered to predict the outflow hydrograph at the outlet of a hypothetically considered ungauged basin. The Muskingum and Cunge-Muskingum approaches are developed as hydrologic routing models. The performance of the hydrologic models is evaluated by comparing the computed outflow hydrograph with the observed hydrograph using nine statistical errors. The peak flow error of the proposed Muskingum approach (MA) is found to be 7.51%. The RMSE, peak flow time error, E-volume, MAE, r-square, RE, NSE, and KGE of MA are 29.064 m3/s, 1.72%, 33.71%, 12.736, 0.82, 33.71%, 0.548, and 0.474, respectively. The r-square value shows acceptable results. The proposed Muskingum approach (MA) shows medium relative error and satisfactory Nash–Sutcliffe efficiency, but the model shows poor performance when the Kling-Gupta efficiency is considered. In the case of the Cunge-Muskingum model, the peak flow error is 39.63%. The RMSE, peak flow time error, E-volume, MAE, r-square, RE, NSE, and KGE of the Cunge-Muskingum model are 41.104 m3/s, 1.72%, 57.28%, 18.779, 0.626, 57.29%, 0.096, and 0.244, respectively. In the case of the Cunge-Muskingum model, the r-square vale is less than 0.7. The proposed model shows a high relative error, unsatisfactory Nash–Sutcliffe efficiency, and poor performance when Kling-Gupta efficiency is considered.

In the present study, kinematic wave model, variable parameter kinematic wave model, diffusive wave flood routing model, and modified dynamic wave model parabolic are used as hydraulic flood routing models. The performance of the hydraulic models is evaluated by comparing the computed outflow hydrograph with the observed hydrograph using nine statistical errors. The peak flow error of the kinematic wave model (KWM) is 34.71% whereas that of the variable parameter kinematic wave model (VPKWM) is 25.33%. The r-square value of both KWM and VPKWM shows acceptable results, i.e., 0.813 (KWM) and 0.78 (VPKWM). The RMSE, peak flow time error, E-volume, MAE, RE, NSE, and KGE for KWM are 35.803 m3/s, 1.72%, 46.62%, 13.679, 46.63%, 0.314, and 0.265, respectively, and those for VPKWM are 30.975 m3/s, 1.72%, 37.93%, 11.96, 37.93%, 0.487, and 0.448, respectively. Both KWM and VPKWM show high relative error, unsatisfactory Nash–Sutcliffe efficiency, and poor performance in Kling-Gupta efficiency. In this study, DWFRM is used as a hydraulic routing model for the prediction of flood hydrograph at the outlet of an ungauged basin. The RMSE, peak flow time error, E-volume, MAE, RE, NSE, and KGE for KWM are 30.487 m3/s, 1.72%, 21.32%, 11.259, 21.32%, 0.503, and 0.491, respectively. The r-square value of DWFRM shows acceptable results, i.e., 0.817. The proposed DWFRM shows medium relative error and satisfactory Nash–Sutcliffe efficiency, but the model shows poor performance while considering Kling-Gupta efficiency. The peak flow error of DWFRM is 20.69%, whereas in the case of the modified dynamic wave model (MDWMP) it is 5.72%. The r-square value of MDWMP is 0.815. The RMSE, peak flow time error, E-volume, MAE, RE, NSE, and KGE for MDWMP are 24.492 m3/s, 1.72%, 9.8%, 8.744, 9.8%, 0.679, and 0.7, respectively. The proposed model (MDWMP) shows low relative error, good Nash–Sutcliffe efficiency, and good performance when Kling-Gupta efficiency is considered.

From the above result, it is clear that out of all the abovementioned models, MDWMP shows better performance. Another advantage of using this model is that all the terms of the momentum equation are incorporated in this model. For unsteady non-uniform flow in an open channel, the proposed modified dynamic wave model (MDWMP) can predict the discharge, cross-sectional area, velocity, and depth of flow at any cross section of the channel. The proposed MDWMP model can be used to develop a rating curve or stage discharge relationship at the required location. Figures 4, 5, and 6 represent the change in cross-sectional area, velocity, and depth of flow with time respectively at the outlet of the Kulsi River Basin. A rating curve is developed at the outlet of Kulsi River Basin for May–June 2010 and presented in Fig. 7.

Fig. 4
figure 4

Change in cross-sectional area with time at outlet of the Kulsi River Basin using MDWMP June 2010

Full size image
Fig. 5
figure 5

Change in velocity with time at outlet of the Kulsi River Basin using MDWMP May–June 2010

Full size image
Fig. 6
figure 6

Change in depth of flow with time at outlet of the Kulsi River Basin using MDWMP, May–June 2010

Full size image
Fig. 7
figure 7

Stage-discharge relationship at outlet of the Kulsi River Basin using MDWMP, May–June 2010

Full size image

Conclusion

This work aims to study the numerical approach for prediction of flood hydrograph at the outlet of an ungauged basin. In this study, the SCS-CN rainfall runoff model is employed to predict the inflow and lateral inflow hydrographs of the hypothetically considered ungauged basin (Kulsi River Basin). Both hydrologic and hydraulic flood routing models are employed to predict the outflow hydrograph at the outlet of the basin. As the widely used Muskingum equation required the previous year inflow and outflow hydrograph to estimate the Muskingum parameters which is hindered due to lack of hydro-meteorological data in case of ungauged basin. An approach is formulated to estimate the Muskingum parameters in an ungauged basin. In this study, the Muskingum method and the modified Muskingum method (Cunge-Muskingum method) are employed as hydrologic routing models, and the kinematic wave model, diffusive wave model, and dynamic wave model are employed as hydraulic routing models to predict the flood hydrograph at the outlet of the Kulsi River Basin; the results obtained are compared with the observed data. The performance of the models is validated by considering nine error statistics, i.e., RMSE, E-peak, peak flow time error, E-volume, MAE, r-square, RE, NSE, and KGE.

The comparative study of the six different simplified flood routing models developed herein reveals that the MDWMP routing model can more accurately predict the flood hydrograph of an ungauged basin. An added advantage of the proposed dynamic wave routing model is the capability to establish the rating curve and to predict the variation of depth, velocity, and cross-sectional area with respect to time at any ungauged downstream river site. With the drastic decline in an in situ streamflow gauging network day by day in real-world river basins due to high operational and maintenance costs, the developed MDWMP routing method is of special relevance as far as the predictions in ungauged basin are concerned. The Muskingum approach (MA) and DWFRM routing models can also suitably be used in the prediction of flood hydrograph at the downstream of an ungauged basin in less gauged river basin reaches. As in these models the local acceleration term and convective acceleration term of the momentum equation are not considered, these models may be considered as less parsimonious than the MDWMP model. However, one may prefer the Muskingum approach (MA) model as this model is one of the simplest and most popular channel routing models. The limitations of the proposed flood routing methods proposed herein form the basis of the future scope of this study as presented below:

  1. 1.

    The proposed flood routing models may be further improved by using the modified SCS-CN method to develop an inflow hydrograph and lateral hydrographs of an ungauged basin.

  2. 2.

    A future scope could include the other numerical schemes to solve the proposed flood routing models.

  3. 3.

    Linear programming, genetic algorithms, fuzzy inference system, radial basis function, machine learning, and other advanced neurocomputing techniques can be explored to improve the performance of the proposed flood routing models.